径流和风对涌潮影响的数值模拟

张舒羽，潘存鸿

(浙江省水利河口研究院，浙江 杭州 310020)

涌潮往往发生在潮差较大的喇叭形河口或海湾，是涨潮波前锋浅水变形的结果。涌潮来临时，其势凶猛，轰轰作响，潮头陡立，犹如一道直立的水墙高速前进，壮观无比。全世界大约有450 个河口或海湾存在涌潮现象［1］，但以钱塘江为最甚。钱塘江涌潮是独特的、宝贵的自然景观和旅游资源，每年秋季大潮，吸引数十万中外游客前往观潮。另一方面涌潮现象对两岸海塘堤防的破坏很严重，危及两岸广大人民的生命财产安全。同时，涌潮也给航运安全造成很大威胁。研究涌潮规律，对于涌潮保护、涌潮防灾具有实际意义。

影响涌潮特征的因素错综复杂，大致可归纳为潮汐、径流、江道地形和气象因素四个方面［2-3］。林炳尧等［4］根据2000年钱塘江实测资料分析了涌潮传播规律，得到了涌潮高度与当地潮差的正比线性关系;赵雪华［5］应用一维涌潮数值模型研究了径流对涌潮高度的影响，认为山水流量增大，对涨潮流有顶托作用，可使涌潮高度稍有增加，但山水流量增大到某一临界值后，涌潮高度反而减小;曾剑等［6］应用神经网格模型分析了盐官站涌潮高度与当地潮差、地形和径流的定量关系，研究结果表明，当上游径流量小于7 000 m3/s 时，盐官涌潮高度随径流量增大而增加;当上游径流量超过此值时，涌潮高度随径流量增大而减小。气象因素对涌潮高度也产生一定影响，尤其是在台风暴潮期间影响较大。其影响主要表现在直接影响和间接影响两个方面:直接影响是气象因素直接增大或减小涌潮高度，当东风持续劲吹时，涌潮高度将增大;间接影响是气象因素通过增减水，从而增大或减小涌潮河段下游潮差来实现的，气象因素对涌潮高度的影响还没有定量的结论［3］。由于缺乏涌潮特征与影响因素的长系列观测资料，并且在实际江道中，影响涌潮特征的因素众多，各影响因素之间并非都是独立变量，不易得到某些因素(如径流、风向风速)对涌潮特征的影响规律。为此，以钱塘江河口为基础，建立概化强潮河口的水动力数学模型，使复杂问题相对简单化，通过数值模拟探讨径流、风向风速对涌潮的影响。

1 涌潮模拟的水动力模型

寻找一个合适的数值模型是模拟涌潮的首要条件。涌潮数值模拟有两个关键问题，一是强间断的模拟。涌潮前后，水位、流速(流量)存在突变，非线性效应很强，常规的数值方法要么数值耗散太大，计算结果将突变的物理量抹平;要么产生数值振荡，甚至失稳。二是方程源项的处理。为准确求解涌潮传播速度，控制方程必须采用守恒型方程，从而带来了方程左端压力项与方程右端底坡源项的“和谐”问题［7］。

采用基于无碰撞二维Boltzmann 方程的KFVS(kinetic flux vector splitting)格式求解二维浅水方程，该格式能模拟间断流动。无碰撞二维Boltzmann 方程:

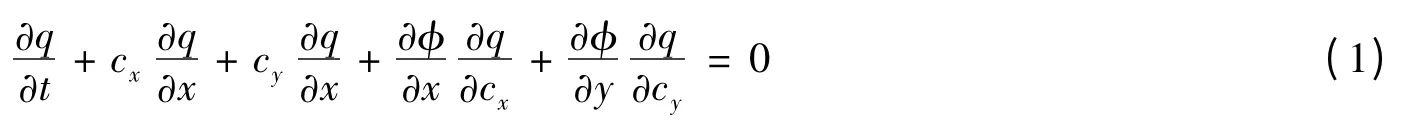
式中:q 为平衡态时分子速度分布函数;cx、cy分别为分子在x、y 方向的分子速度;φ 为外力作用项，这里考虑非平底引起的重力、阻力、风应力、柯氏力和盐度密度引起的压力等外力。

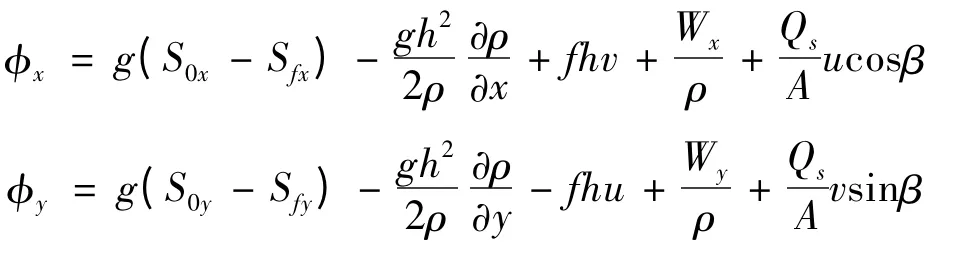
式中:g 为重力加速度;Sfx、Sfy分别为x、y 方向的阻力项;S0x、S0y分别为x、y 方向的底坡项;ρ 为盐水密度;f 为柯氏系数;Wx、Wy分别为x、y 方向的风应力;Qs为取(排)水口的水流流量;β 为取(排)水方向与x 轴的夹角。

式(1)不考虑碰撞项的结果是，其推得的对应控制方程没有计及二阶粘性项。将式(1)乘以(1，cx，cy)T，并对分子速度空间积分，利用水流宏观变量水深h，x 和y 方向的流速u、v 与分子微观变量f、cx、cy的关系:

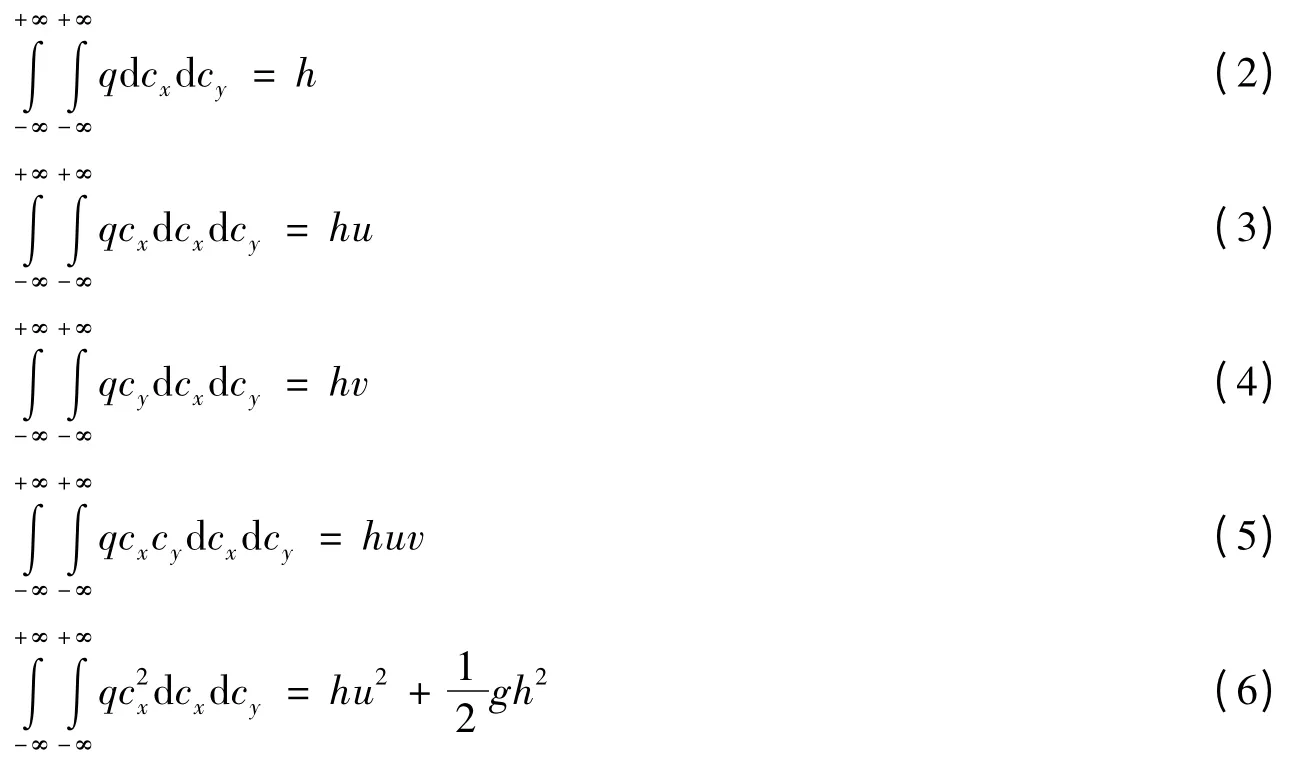
可得控制方程

式中:

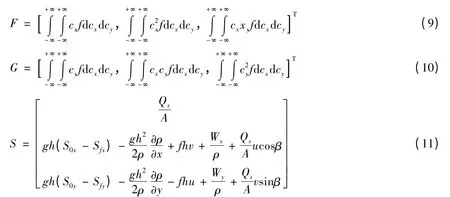
采用无结构三角形单元离散，并采用网格中心格式。设Ωi为第i 个三角形单元域，Γ 为其边界，对式(7)应用有限体积法离散，经推导可得基本数值解公式［8］

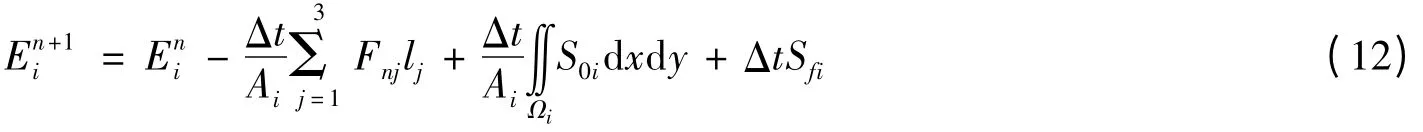
式中:Ai为三角形单元Ωi的面积;Fn=Fcosθ +Gsinθ，(cosθ，sinθ)为Γ 外法向单位向量;Δt 为时间步长;下标j 表示i 单元第j 边;lj为三角形边长;上标n 为时间步。

求解式(12)的核心是法向数值通量的计算、底坡源项的处理，以及动边界处理［3］。这里应用能模拟间断流的干底Riemann 解处理动边界问题。上述模型已经经典算例和实际问题的应用检验［3，8-10］。

2 模型概化

以钱塘江富春江电站至芦潮港的江段为原型，按照电站、闻家堰、闸口、七堡、仓前、盐官、澉浦、乍浦、芦潮港断面的平均高程和河宽对概化模型进行控制，忽略断面上河床地形的变化，构造一个轴对称的概化模型，见图1，沿河道纵向的地形见图2。模型构造需考虑钱塘江涌潮形成的2 个基本条件［2］:一是钱塘江河口在平面上的急剧收缩使潮波能量积聚，潮差增大;二是乍浦以上的水下沙坎堆积，使水深迅速减小，潮波浅水效应增强。概化模型电站到芦潮港全长278 km，其中闻家堰至澉浦长116 km。各控制断面的河宽采用实际河宽，从下往上平面上急剧收缩。自乍浦以上，河床高程抬高，至仓前达到最高，而后至闻家堰高程降低。由此可见，构造的概化模型满足涌潮发生的两个条件。概化模型下边界芦潮港采用正弦函数来模拟潮汐过程，周期12 h，潮差3 m。模型计算域采用三角形网格离散，三角形单元194 432个，节点99 625 个，最小空间步长50 m，位于关注区域闻家堰～盐官河段，计算时间步长0.5 s。涨潮糙率0.002 ～0.02，落潮糙率0.003 ～0.03。概化模型在盐官位置涌潮高度可达2.4 m左右。

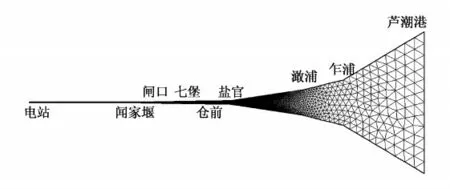
图1 概化模型网格示意Fig.1 Grid of generalized model

3 涌潮传播规律

当上游电站流量为500 m3/s，下游芦潮港潮差为3 m，无风情况下时，绘出反映涌潮传播规律的特征图并阐述规律如下:

图3 绘出了高、低潮位、潮差和涌潮高度的沿程变化。盐官至仓前，河底坡度大，潮波在传播过程中，高、低水位均向上游迅速抬升，低潮位的抬升值大于高潮位，潮差沿程递减。仓前至闻家堰，高潮位变化不大，低潮位继续缓慢抬升，潮差减小。盐官至七堡，涌潮高度沿程减小，七堡至闻家堰，涌潮高度略有增加。

图4 绘出了代表站位潮位随时间的变化过程。涌潮到达时，水位迅速抬升，如盐官站水位迅速上升2.42 m，七堡站水位迅速上升1.76 m。

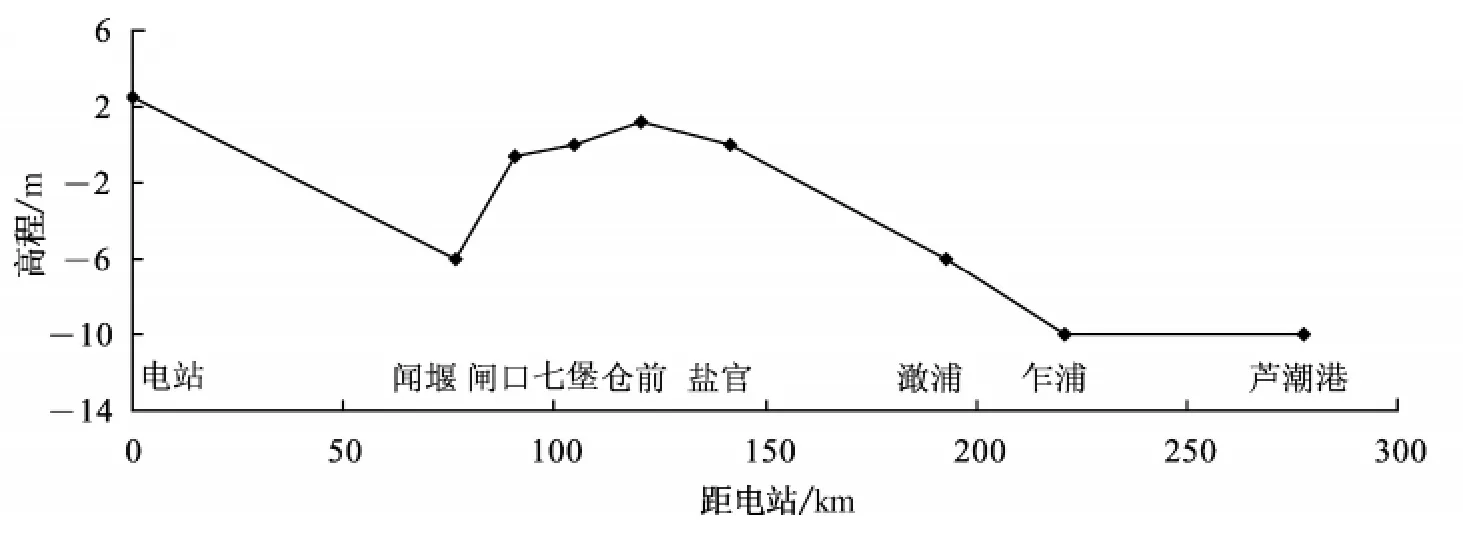
图2 纵向地形示意Fig.2 Schematic diagram of longitudinal terrain

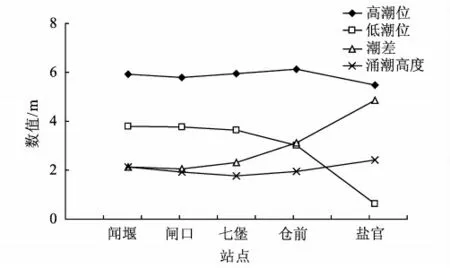
图3 高低潮位、潮差和涌潮高度沿程变化Fig.3 Variation of high and low water level，tidal range and tidal bore height along the river

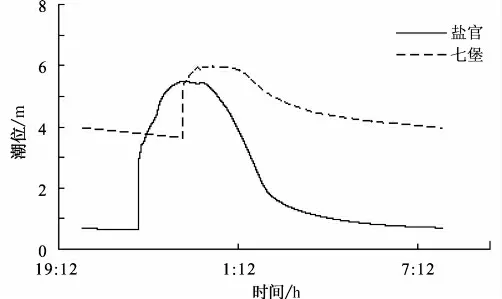
图4 代表站位潮位过程线Fig.4 Tidal level of representative station

图5 绘出了每间隔1 h 沿程水面线的变化。从图中清晰可见每个时刻涌潮到达的位置。涌潮到达时，水面迅速抬升。在图中所示的3 h 里，涌潮行进了74 km。

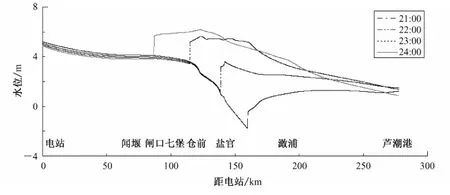
图5 不同时刻水面线Fig.5 Water surface profile at different time

4 不同径流下涌潮特征变化规律

上游径流量采用500、1 000、5 000、7 000、10 000 m3/s 进行计算，各特征值的统计结果:根据计算，当流量超过7 000 m3/s，概念模型里七堡上游无涨潮流;当流量超过10 000 m3/s，仓前上游无涨潮流。各流量下涨落潮差、涨落历时、涌潮高度特征值见表1。各流量下沿程各站涌潮高度的变化见图6。一般情况下，上游流量越小，沿程各站潮差越大。当流量小于1 000 m3/s 时，涨潮历时的变化差异不大;当流量继续增加，涨潮历时一般随着流量的增加而减小，但当流量超过7 000 m3/s，七堡以上只有水位的抬升和下降，而无涨潮流，当上游流量继续增加，七堡以上水位抬升的时间随着流量的增加而增加。涌潮高度的最大值上下游河段有所不同，在下游盐官、仓前站，涌潮高度在5 000 m3/s时达到最大，在上游七堡、闸口、闻家堰，涌潮高度在1 000 m3/s 达到最大。说明在径流不大时，涌潮高度随着径流的增加而增加，到达一定临界流量后，水深加大，受下泄流量顶托，潮汐减弱，涌潮高度反而降低，并且降低幅度较大。这与文献［6］的结论在定性上是一致的;越往上游，临界流量值越小。以盐官、七堡为代表，画出各流量下潮位随时间的变化见图7。涌潮到达时，潮位迅速抬高;流量越大，涨潮时间越滞后。

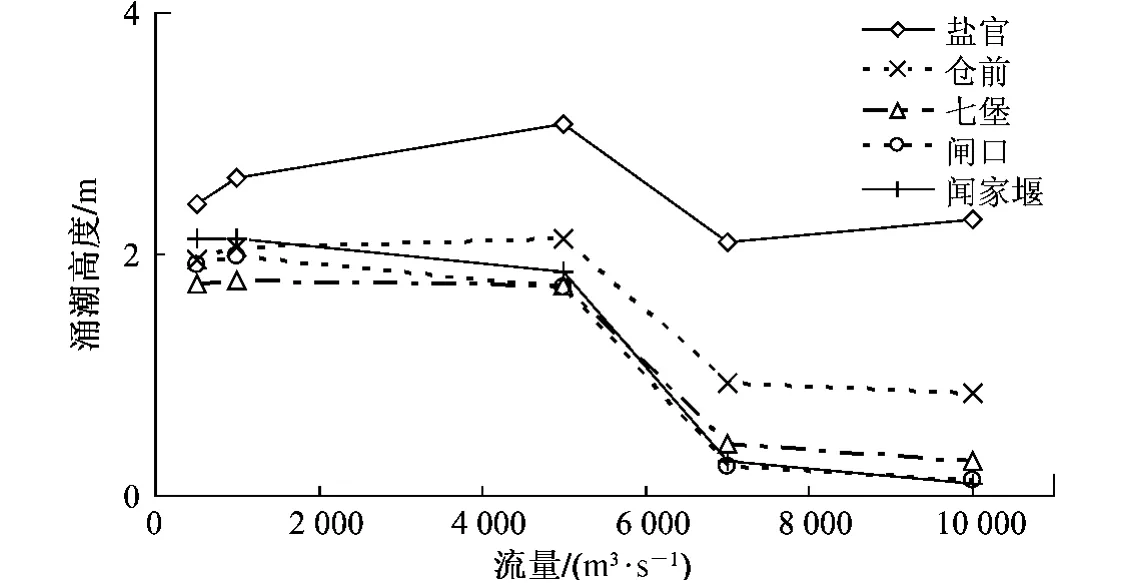
图6 各流量下沿程涌潮高度Fig.6 Tidal bore height along the river under different discharges

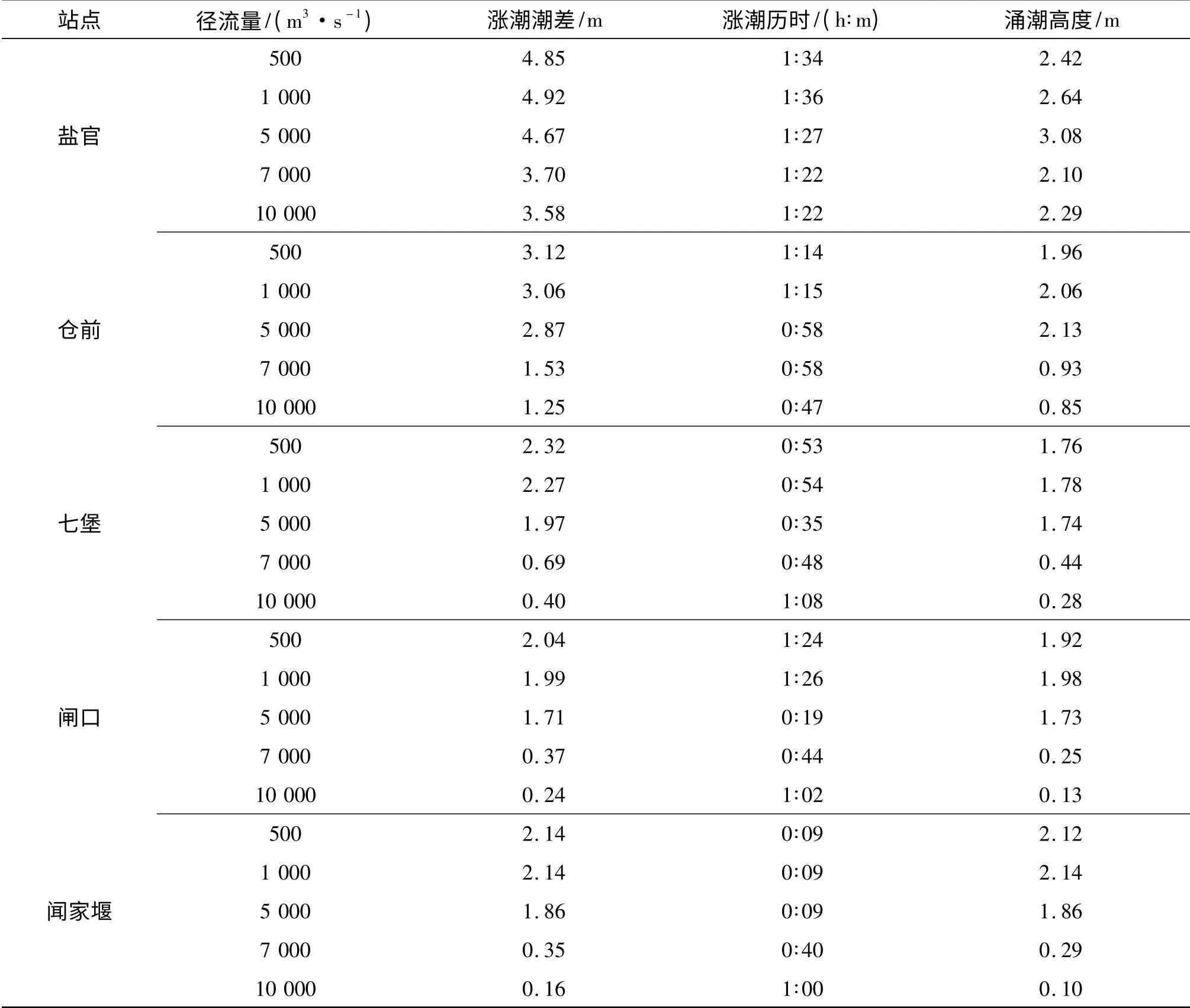
表1 各流量下涌潮特征值Tab.1 Characteristic values of tidal bore under different runoffs

涌潮传播速度指涌潮潮头的行进速度。根据计算结果，统计各流量下各区段的涌潮传播速度见表2。同一流量下，下游的潮波传播速度小于上游的速度。同一区段，随着流量的增加，大部分情况潮波传播速度随着流量的增加而减小，但仓前～七堡在5 000 m3/s 时潮波传播速度达到最大。根据文献［3］分析，涌潮传播速度c 为:

式中:h 为水深;Δh 为涌潮高度;u 为流速;下标d 和u 分别标识下游侧和上游侧。

由式(13)可见，涌潮传播速度与涌潮前落潮流速uu、涌潮高度Δh、潮前水深hu和潮后水深hd等因素有关。随着上游径流量的增大，uu绝对值增大，hu增大，hd变化相对较小，Δh 变化有增有减，如图6 所示，表2为各流量下涌潮传播速度的数模计算结果，由表可知，盐官以上河段c 随着径流量的增大而减小;而澉浦～盐官河段，由于径流量从500 m3/s 增大到5 000 m3/s 时Δh 增大较多，导致在这一流量区间c 变化不大，而当径流量增大到7 000 m3/s 以后，因uu、hu和Δh 三个因子均促使c 减小，从而c 急剧下降。因此，数模计算结果与解析式(13)的分析结果是一致的。

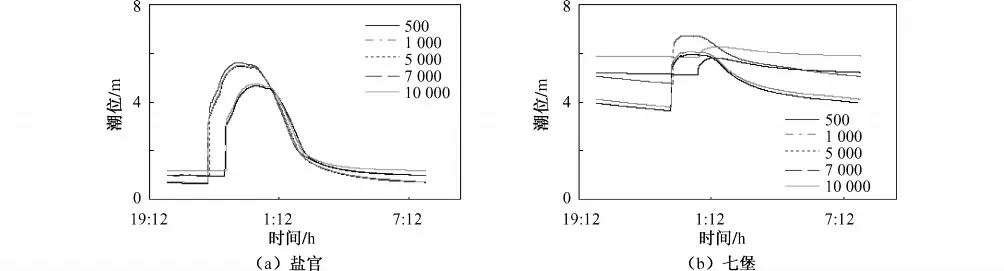
图7 代表站位各流量下潮位过程线Fig.7 Tidal level hydrograph of representative stations under different discharge

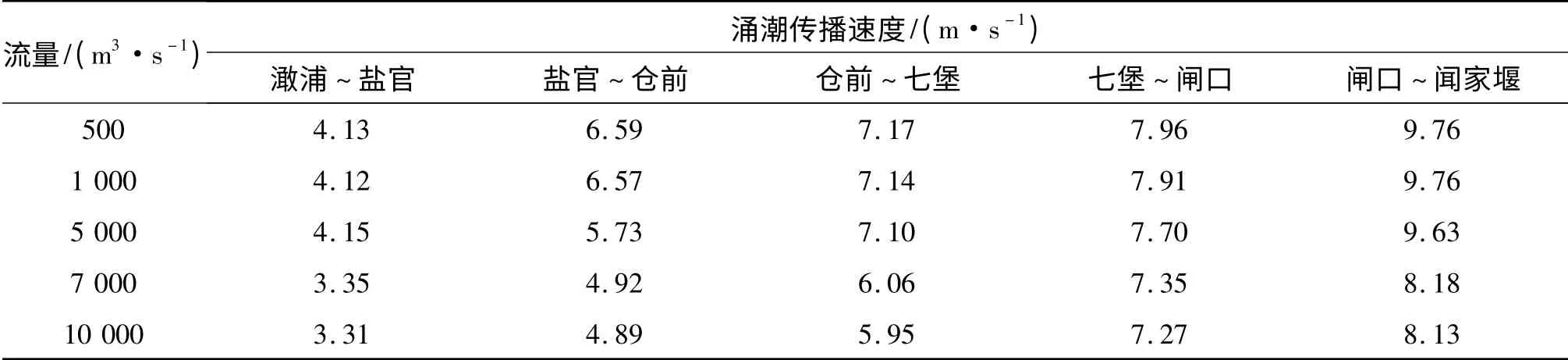
表2 各流量下涌潮传播速度Tab.2 Propagation velocity of tidal bore under different discharges

5 不同风况下涌潮特征变化规律

5.1 不同风向下涌潮特征变化规律

加风时间为盐官低潮位前2.5 h，风速15 m/s，上游径流500 m3/s。计算了东风、西风、无风三种工况。加风后潮汐特征见表3 和图8。

由图8 和表3 可见，风向对潮差、涌潮高度、涨潮历时和涌潮传播速度影响很大，无论是潮差、涌潮高度还是涨潮历时和涌潮传播速度，均是“西风(逆风)”＜“无风”＜“东风(顺风)”。各站影响程度有所不同，如盐官站“东风”方案潮差比“无风”方案大0.83 m，增大17%;“西风”方案潮差比“无风”方案小0.90 m，减小18%;“东风”方案比“西风”方案潮差大1.73 m，增大44%。盐官站“东风”方案涨潮历时比“无风”方案延长0∶43，增大46%;“西风”方案涨潮历时比“无风”方案缩短0∶15，减小16%;“东风”方案比“西风”方案涨潮历时长0∶58，增大73%。盐官站“东风”方案涌潮高度比“无风”方案大0.02 m，仅增大1%;“西风”方案涌潮高度比“无风”方案小0.21 m，减小9%;“东风”方案比“西风”方案涌潮高度增大10%。

一般而言，因上游吹程远，风的作用增大，以闸口站为例，“东风”方案潮差比“无风”方案大1.20 m，增大59%;“西风”方案潮差比“无风”方案小0.95 m，减小47%;“东风”方案比“西风”方案潮差大2.15 m，增大197%。“东风”方案涨潮历时比“无风”方案延长0∶01，增大1%;“西风”方案涨潮历时比“无风”方案缩短1∶21，减小96%;“东风”方案比“西风”方案涨潮历时长1∶22，增大2 800%。“东风”方案涌潮高度比“无风”方案大0.50 m，增大26%;“西风”方案涌潮高度比“无风”方案小0.83 m，减小43%;“东风”方案比“西风”方案涌潮高度增大122%。

表3 各风向下涌潮特征值Tab.3 Characteristic values of tidal bore under different wind directions

在风速15 m/s 条件下，“西风”方案沿程涌潮传播速度比“无风”方案减小6% ～13%，“东风”方案沿程涌潮传播速度增加5% ～9%。为检验这一结果的合理性，对实际发生的台风期及台风前的情况进行统计对比，如表4。钱塘江台风期间风向为东偏北，实测资料表明，台风期涌潮传播速度普遍快于台风前，由于实际台风的风速风向均随时间而变，变化复杂，因此台风期涌潮传播速度的增加幅度各次台风相差较大。但在定性上，概化模型计算得到的涌潮传播规律与实际一致。另外，在台风期间，经常形成较高的高潮位、大潮差和强涌潮，计算结果也解释了这一现象。就涌潮传播速度而言，概化模型和实际情况相比，主要有两点不同。一是河口进行对称概化后，潮流上溯的阻力减少，潮波上溯速度变快，动力变强;二是概化的模型在横断面上没有深槽和浅滩的变化，阻力减少，潮波上溯速度变快。如表2 和表4，概化模型中，流量500 m3/s 时，盐官到仓前的涌潮传播速度为6.59 m/s;实际台风作用下，表4 所列的实际江道中发生的涌潮最大传播速度为5 m/s。

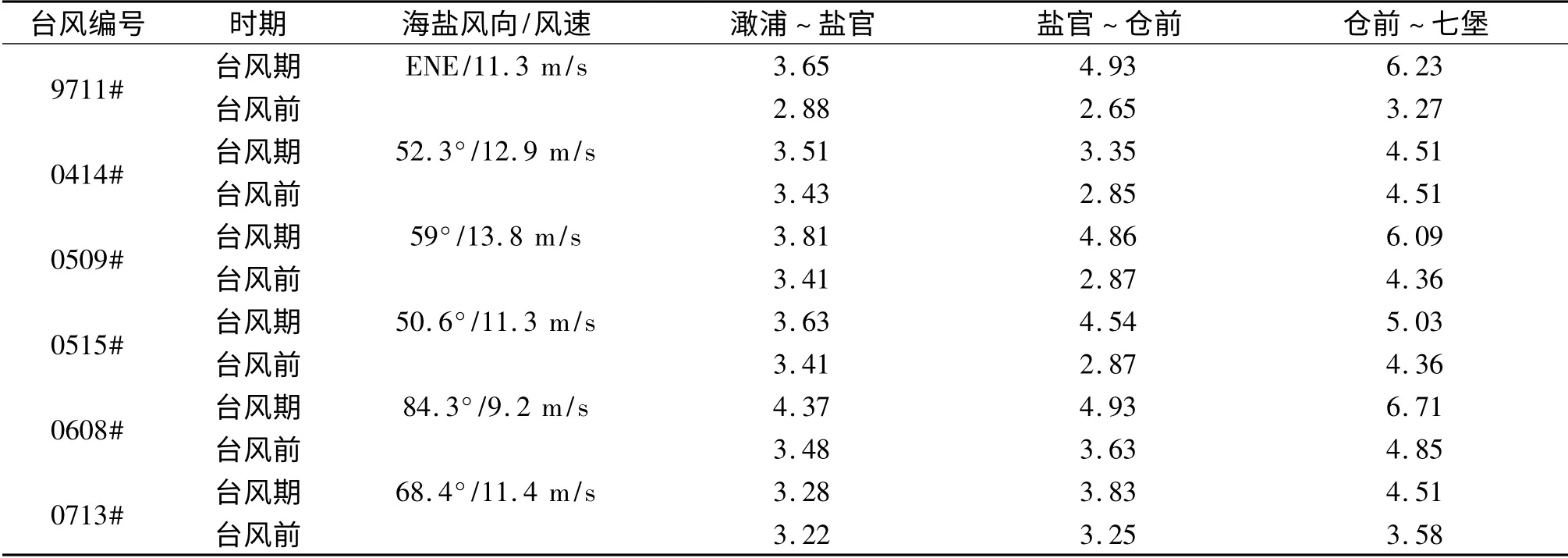
表4 台风前后潮波传播速度Tab.4 Propagation velocity of tidal bore before or after typhoon

5.2 不同风速下涌潮特征变化规律

加风时间为盐官低潮位前2.5 h，上游径流500 m3/s 下，计算了无风、东风风速7.5 m/s，东风风速15 m/s三种工况。加风后潮汐特征见表5 和图9。

由图9 和表5 可见，无论是潮差、涌潮高度还是涨潮历时和涌潮传播速度，均是“无风”＜“东风风速7.5 m/s”＜“东风风速15 m/s”。风速在7.5 m/s 以下，风速对以上涌潮特征值的影响相对小一些，风速在15 m/s以上，对涌潮特征值的影响较大。如盐官站“东风7.5 m/s”方案潮差比“无风”方案大0.14 m，增大3%;“东风15 m/s”方案潮差比“无风”方案大0.83 m，增大17%。盐官站“东风7.5 m/s”方案涨潮历时比“无风”方案延长0∶09，增大10%;“东风15 m/s”方案涨潮历时比“无风”方案延长0:43，增大46%。盐官站“东风7.5 m/s”方案涌潮高度比“无风”方案大0.01 m，“东风15 m/s”方案涌潮高度比“无风”方案大0.02 m。

“东风7.5 m/s”方案沿程涌潮传播速度比“无风”方案增加0.7% ～4%，“东风15 m/s”方案沿程涌潮传播速度增加6% ～9%。

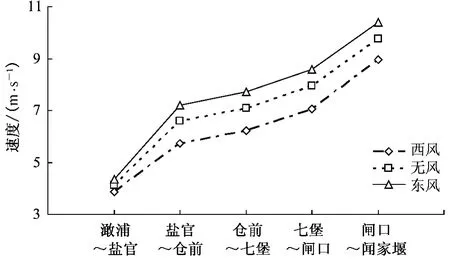
图8 各风向下潮波传播速度Fig.8 Propagation velocity of tidal bore under different wind directions

图9 各风速下潮波传播速度Fig.9 Propagation velocity of tidal bore under different wind speeds

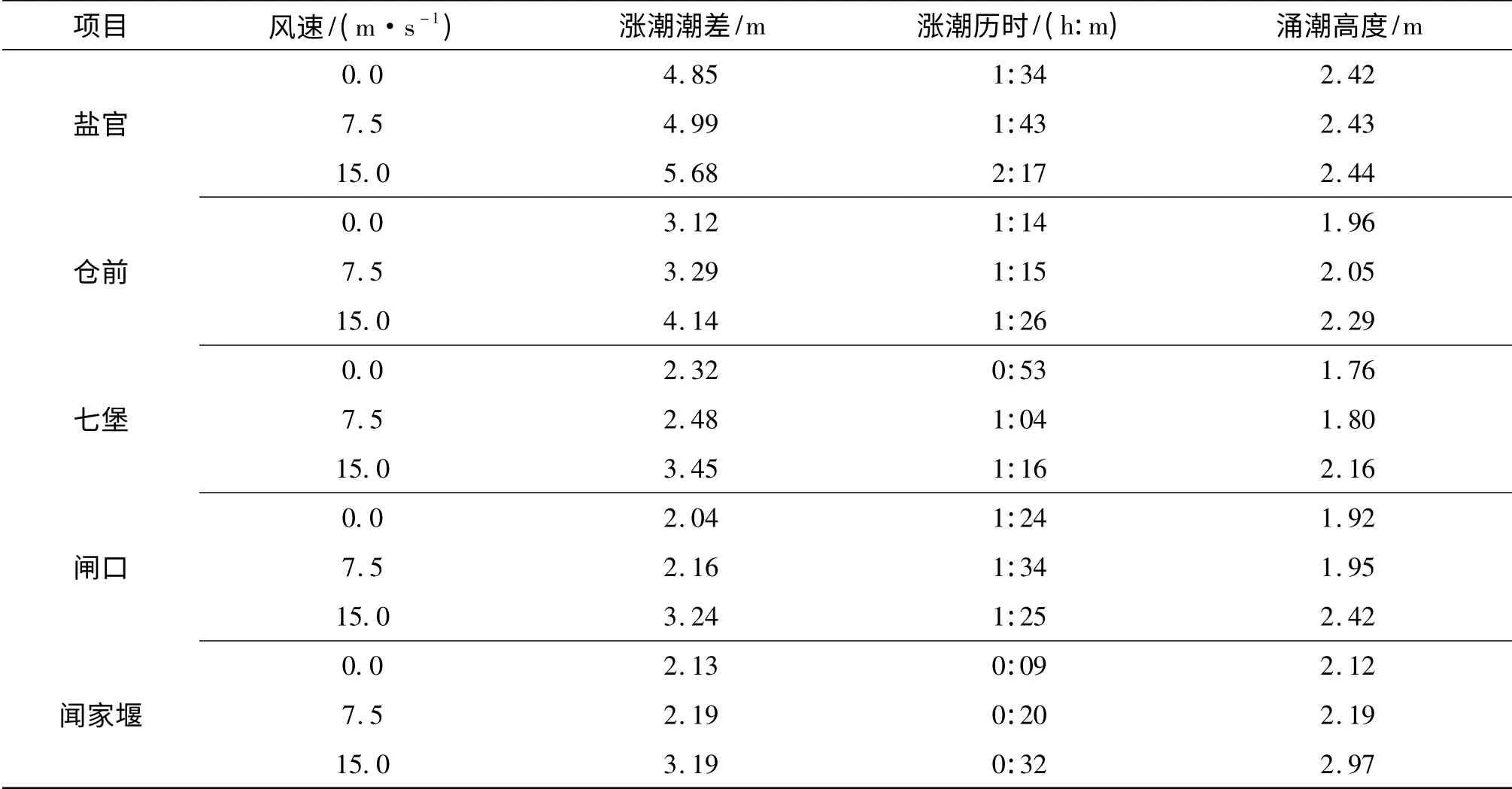
表5 各风速下涌潮特征值Tab.5 Characteristic values of tidal bore under different wind speed

6 结 语

以钱塘江河口平面尺度和河床地形为基础，建立了概化河口的二维水动力数学模型，通过数值试验探讨了径流、风向对涌潮的影响。主要结论如下:

1)径流量对涌潮的影响。上游流量越小，沿程各站潮差越大。当流量小于1 000 m3/s 时，涨潮历时的变化差异不大;当流量继续增加，涨潮历时一般随着流量的增加而减小。径流量对涌潮高度的影响比较复杂，不同河段存在涌潮高度最大值的相应临界径流量，越往下游，临界径流量越大，在下游盐官、仓前站，涌潮高度在5 000 m3/s 时达到最大，在上游七堡、闸口、闻家堰，涌潮高度在1 000 m3/s 达到最大。涌潮传播速度与潮前、潮后水深、涌潮高度和潮前落潮流速有关，大多情况下涌潮传播速度随着径流量的增大而减小。

2)风况对涌潮的影响。计算结果表明，潮差、涌潮高度、涨潮历时和涌潮传播速度，均是“西风(逆风)”＜“无风”＜“东风(顺风)”。根据台风期间调研和实测资料分析，计算结果与实际情况符合。顺风条件下，风速越大，涌潮高度越大。

3)涌潮传播规律研究成果是基于定床下的概化模型，在各流量下，地形对流量有不同的响应，如洪水期上游江道冲深，下游淤积，致涌潮传播规律也会有所差异，这个影响有待于下一阶段进行研究。

［1］Chanson H.Current knowledge in tidal bores and their environmental，ecological and cultural impacts［J］.Environmental Fluid Mechanics，2011，11:77-98.

［2］韩曾萃，戴泽蘅，李光炳.钱塘江河口治理开发［M］.北京:中国水利水电出版社，2003.

［3］潘存鸿，鲁海燕，曾 剑.钱塘江涌潮特性及其数值模拟［J］.水利水运工程学报，2008(2):1-9

［4］林炳尧，黄世昌，毛献忠，等.钱塘江河口潮波变化过程［J］.水动力学研究与进展:A 辑，2002，17 (6):665-675.

［5］赵雪华.几项主要因素对钱塘江涌潮形成和发展的影响［R］.杭州:浙江省河口海岸研究所，1982.

［6］曾 剑，熊绍隆，潘存鸿，等.运用神经网络理论研究钱塘江涌潮的影响因素［J］.长江科学院院报，2006，23(5):14-16，20。

［7］潘存鸿.浅水间断流动数值模拟研究进展［J］.水利水电科技进展，2010，30(5):78-84.

［8］潘存鸿，徐 昆.三角形网格下求解二维浅水方程的KFVS 格式［J］. 水利学报，2006，37(7):858-864.

［9］潘存鸿，于普兵，鲁海燕.浅水动边界的干底Riemann 解模拟［J］.水动力学研究与进展:A 辑，2009，24(3):305-312.

［10］潘存鸿，鲁海燕.二维浅水间断流数值模型在涌潮模拟中的应用［J］.浙江大学学报:工学版，2009，43(11):2107-2113.