基于贝叶斯网络的钻井井漏问题研究

2013-11-22徐哲李建王兵西南石油大学计算机科学学院四川成都610500

石油天然气学报 2013年12期

徐哲，李建，王兵（西南石油大学计算机科学学院，四川成都 610500）

刘昆（中国石油集团测井有限公司生产测井中心第二项目部，陕西西安 710077）

井漏是钻井时发生的一种井下复杂情况，也是钻井过程中最普遍最常见的技术难题之一，其中井漏因素的不确定性给研究带来了一定的难度［1］。贝叶斯网络就是为处理不确定性问题而发展起来的［2］，它是一种将概率统计应用于复杂领域进行不确定性推理和数据分析的工具，其主要优点就是推理结果的正确性，且只需建立一个联合概率分布，这个过程可以将性能参数中的各个关系通过联合概率分布表示出来，贝叶斯网络就是将复杂的联合概率分布分解成一系列相对简单的模块，从而大大降低了知识获取和概率推理的复杂度。

1 钻井井漏

钻井过程中，井筒内钻井液或其他介质（固井水泥浆等）漏入地层孔隙、裂缝等空间的现象称为井漏。井漏是钻井工程中常见的井内复杂情况，多数钻井过程都有不同程度的漏失。严重的井漏会导致井内压力下降，影响正常钻井，引起井壁失稳，诱发地层流体涌入井筒并井喷。

1.1 发生井漏的影响因素

在钻完井过程中，以下两种情况会发生井漏。一是地层存在天然的漏失通道，井筒内的钻井液作用于井壁地层的动压力超过地层漏失压力；二是井筒内钻井液作用于井壁的动压力大于地层破裂压力时，形成新的漏失通道。因此，井壁地层的动压力、地层漏失压力、地层破裂压力都影响钻井井漏的发生。

影响漏失压力的因素［3，4］：①地层孔隙压力的大小；②地层天然漏失通道大小、形态与漏层厚度；③钻井液的流变性能；④地层漏失通道中流体的流变性；⑤井壁地层内、外泥饼质量。

影响地层破裂压力的因素为地层岩石所受地应力大小。

影响井壁地层动压力的因素：①钻井液静液柱压力；②钻井液环空流动压耗；③钻井液激动压力。

1.2 钻井液漏失的原因以及应对方法

钻井液在漏失通道中有4个力对其作用，分别是钻井液的静压力pw，钻井液流动时对井壁的侧压力pa，地层孔隙中水的压力po，漏失通道对钻井液流动的阻力pL。钻井液漏失的前提是井壁有漏失通道且漏失通道相互贯通，其次是钻井压力（pw＋pa）大于地层系统压力（po＋pL），即 Δp ＝（pw＋pa）－（po＋pL）＞0。像钻井液的静压力pw、侧压力pa、流动阻力pL都是变化的，而地层压力po是不变的。

从客观的角度去想就是钻井液静止时不漏，可循环时漏，就是因为钻进循环时增加了一侧压力pa，使Δp＞0，从而发生井漏。

漏失通道中的4个作用力难以被度量，使得研究井漏发生的问题更加困难。应对钻井液发生漏失问题的方法有很多，知名的有神经网络，模糊数学，正、反循环测试计算等方法。由于神经网络在数据不充分时无法进行工作，难以将一些推理变为数值计算，模糊数学的评价模型以及评价指标权重难以建立，正、反循环测试计算不能解决井漏发生前的问题，所以引入贝叶斯网络来有效解决井漏发生的不确定性问题。

2 贝叶斯网络

贝叶斯网络是一个有向无环图（DAG）［5］，它是随机变量集组成的网络节点，变量可离散或连续，是一个连接节点对的有向边或箭头集合。贝叶斯网络的每个节点Xi都有一个条件概率分布表（CPT）：P（Xi｜pa（Xi）），能量化其父节点对该节点的影响。由此可见，有向无环图是贝叶斯网络的定性部分，蕴含了条件独立性的假设；条件概率表是贝叶斯网络的定量部分，表征了节点间的相互关系强度。贝叶斯网络特性中最具有印象的是能够作为对域的一种完备而无冗余的表示，它能比全联合概率更加紧凑。

2.1 贝叶斯网络的数学模型

贝叶斯网络是一种由因果知识和概率知识结合的信息表示框架，它是由条件概率表和有向无环图表示的一种不确定的知识表达与推理模型。形式上说，一个贝叶斯网络是一个二元组S＝〈G，P〉［6，7］＝〈V，E，P〉，在这里还要考虑一个有限的离散随机变量集合U＝｛X1，X2，…，Xn｝。其中，第1部分G就是一个有向无环图，其中的节点与随机变量X1，X2，…，Xn一一对应，有向边表示变量之间是条件依赖关系。第2部分P是筹划网络局部条件概率的参数集合Pi（vi｜pa（vi）），pa（vi）表示节点vi的父节点集。E为有向边的集合，表示各节点间的因果联系。

贝叶斯网络数学模型的构造分3个部分。第1部分是确定建立网络数学模型有关的变量：①需要确定模型的目标；②确定与问题有关的可能观测值，并确定其中要建立模型的子集；③将这些观测值组织成互不相容的而且穷尽所有状态的变量。第2部分是建立一个表示条件独立的有向无环图。根据概率乘法公式有：

对于每个变量Xi如果有某个子集∏i⊆ ｛X1，X2，…，Xi－1｝使得Xi与｛X1，X2，…，Xi－1｝＼∏i是条件独立的，就对任何X有：

2.2 贝叶斯网络的推理以及XML技术的引入

当网络比较复杂时，就肯定要用到推理。贝叶斯网络的推理主要是计算条件概率P（XQ｜XE＝xE），XQ是询问变量集合，XE是证据变量的集合。根据贝叶斯公式可得：

2.2.1 变量消元算法

最经典的贝叶斯网络推理就是变量消元算法（变量消除算法），具体用一个贝叶斯网络的实例来分析，如图1所示。

根据联合概率分布分解，然后对变量求解边缘概率分布，具体描述为：

图1 贝叶斯网络实例

按照从右至左的顺序消除各变量，消除变量G得到：

2.2.2 引入XML技术

XML是可扩展标记语言［8］，它是用于标记电子文件使其具有结构性的标记语言，它是一种允许用户对自己的标记语言进行定义的源语言，可用来标记数据，定义数据结构。

XML所描述的结果是一种可供人阅读的文档，它的简单结构使其易于在任意应用程序中读写数据。XML能够以灵活有效的方式定义管理信息的结构，不过它也有一些限定的语法，标签必须按合适的顺序进行嵌套，而不是简单的前后次序关系。贝叶斯网络这种数据结构采用XML来描述：

XML文件能够很好地描述每个节点的信息，这样就能直接用XML文件来编写贝叶斯网络中先验概率的录入，接着可以通过程序平台计算显示相应的后验概率。

3 贝叶斯网络应用于钻井井漏

贝叶斯网络可以表达不确定知识，同样能进行概率推理，其学习算法能够从很多数据中构建网络。贝叶斯网络非常适合不确定事物的发现，将贝叶斯网络用于处理钻井井漏的问题有很多优势，它能发现隐含性的东西，具有良好的逻辑性和可推理性，它简化了概率的运算，最重要的是能进行因果双向推理。

3.1 贝叶斯网络模型的建立

发生井漏的根本原因是钻井液液柱压力大于地层压力，考虑各个因素引起井漏的共因关系和相关关系可得出贝叶斯网络模型。贝叶斯网络应用于钻井发生井漏的基本框架如图2所示，即钻井发生井漏的贝叶斯网络。

3.2 条件概率表的建立以及推理逻辑分析

图2 贝叶斯网络应用于钻井井漏的基本框架

一个完整的贝叶斯网络，除了以上的网络架构外，还需要构建钻井发生井漏各因素间的条件概率表，这里可以使用数据分析来构建整个网络，而相应的算法比较知名的有K2算法［9］，变量消除算法等。贝叶斯网络各个节点的概率分布可以通过数据分析得到，也可以通过问题的特性直接得到。贝叶斯网络的后验概率是根据先验概率来计算的。

依照网络结构图，分别用以下字母表示可能引起井漏的一些因素。τ为钻井液静切力；Fi为钻具惯性力；Fv为钻井液黏滞力；ρ为钻井液密度；H为垂直深度；I为钻井液流变性能；ps为钻井液激动压力；psl为钻井液静液柱压力；pa为钻井液环流流动压耗。

根据井漏发生事故的原因——后果分析［10］数学模型转化为有向无环图后建立条件概率表，钻井井漏各个因素引起异变的先验概率值根据所给资料数据［3，4］计算总结所得。表1是对川东北地区油田的几口井研究所计算的先验概率：钻井液在压差的作用下，无论是地层中的液体压力将钻井液压入漏失通道，还是存在天然漏失通道的情况都考虑进去。

表1 1年川东北地区几口井钻井液发生漏失时各个因素异变的概率估计值表

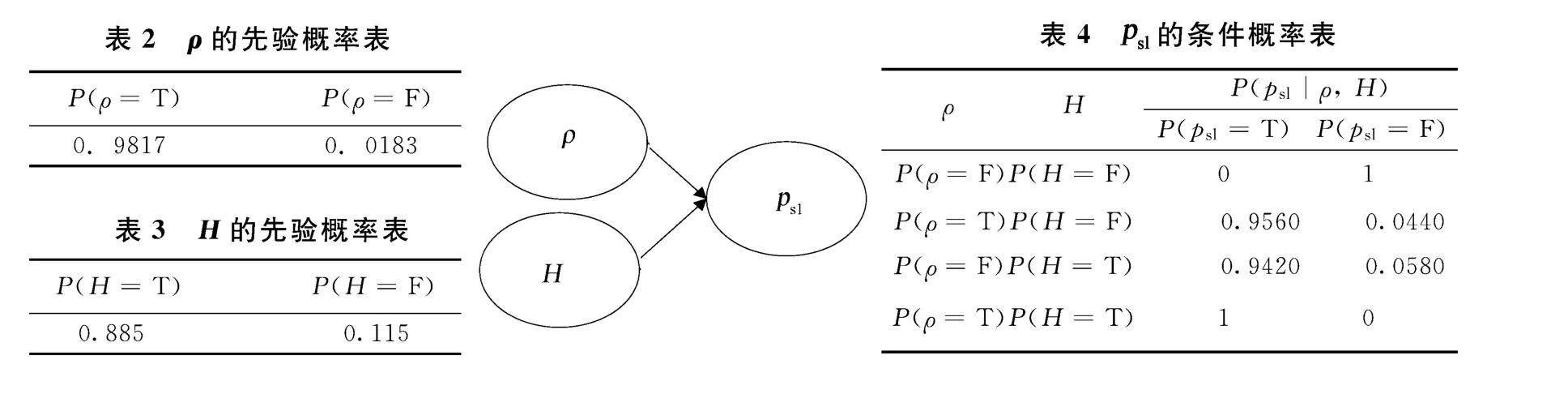
图3 贝叶斯网络某个局部位置的有向无环图与条件概率表

图3的计算结果列出了局部的ρ、H、psl这3个变量所需的先验概率，其余的因素考虑用变量消元法去推理。对大量的数据进行统计，求算先验概率，钻井液密度大于等于1.13g／cm3的概率为P（ρ≥1.13），用P（ρ＝T）表示，小于1.13g／cm3的概率为P（ρ＜1.13），用P（ρ＝F）表示。井段的垂直深度在2800～3520m范围的概率为P（2800＜H＜3520），用P（H＝T）表示，不在2800～3520m范围的概率为P（（H＜2800）∪（H＞3520）），用P（H＝F）表示。对于静液柱压力来说，与钻井液密度和垂直深度是成正比的，所以只要任何一个升高，它都会升高。所有的变量因素不在正常值的范围内叫异变。

计算P（psl＝T｜ρ，H）的后验概率，根据变量消元法，此处是3个变量，利用式（4）、（5）可得联合分布分解f＝｛P（ρ）、P（H）、P（psl｜ρ，H）｝，采用先消去ρ后消去H，利用上述表中的先验概率可得P（psl＝T）＝0.9949，可见静液柱压力总体还是处于正常值。整个钻井井漏的贝叶斯网络架构非常复杂，要计算井漏的后验概率较困难，对整个联合分布进行分解来降低概率推理的复杂性，还是用前面的变量消元算法来一个一个地消除变量计算后验概率。以表1数据中的先验概率为依据，然后根据式（3）、（5）编写出消元算法的程序代码，一层一层地代入，以Windows窗体为界面用于显示计算后验概率的结果。在这个程序运行结果中要调用前面所说XML文件到文本框里，可将上面的数据代入验证。

因为整个模型结构的复杂化，所以影响井漏的因素考虑的不是很全面，会造成不同钻井液体系所计算的后验概率存在误差。对整个网络依据式（5）编好的程序算法按合理的顺序消元对考虑钻具惯性力与不考虑钻具惯性力所计算的钻井液发生漏失的概率存在很大误差（19.23%和13.14%）。由此可见向贝叶斯网络添加一个因素会使各因素间的依赖关系、共因关系更明确。

3.3 钻井井漏用贝叶斯网络计算结果的分析

贝叶斯网络在计算时要尽可能地考虑各个因素的相关关系，这样在使用不同钻井液体系时发生井漏的概率会明显不同，不同体系（主要因素是密度）导致的流变性能不一样。单考虑因果关系会忽略各个因素之间的依赖关系，这就使得计算结果偏小而造成误差。从上面钻井发生井漏的实例来看，还是存在一些误差的。贝叶斯网络能够较好地描述各因素间的相关关系，这是一些只考虑变量间因果关系的模型所做不到的。