关于Gauss-Kronecker曲率为零的极小超曲面的注记
2013-11-21马红娟赵秀兰郑喜英
马红娟,赵秀兰,郑喜英
(黄河科技学院信息工程学院,中国 郑州 450063)
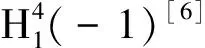
定理1[7]设M3是数量曲率有下界的完备可定向三维黎曼流形,f:M3→R4是满足Gauss-Kronecker曲率恒为零,第二基本形式恒不为零的等距极小浸入,则f(M3)可分解为黎曼直积L2×R,L2是R3中高斯曲率有下界的完备极小超曲面.
上述分类定理对数量曲率和第二基本形式加了很强的条件.如果f:M3→R4是完备极小超曲面,f(M3)可分解为L2×R,其中L2是R3中的完备极小曲面,那么M3的数量曲率一定有下界吗?本文通过具体例子说明上述定理中的部分条件是不必要的,并给出分类定理.
1 准备知识
设f:M3→R4是定向极小超曲面,截面曲率为零,选取{e1,e2,e3,e4}为正交标架,对偶标架{ω1,ω2,ω3,ω4},联络形式{ωij},约定1≤i,j≤3,主曲率满足k1=k>k2=0>k3=-k,k>0,数量曲率和Gauss-Kronecker曲率分别由下式确定:
H=k1k2+k1k3+k2k3,K=k1k2k3.
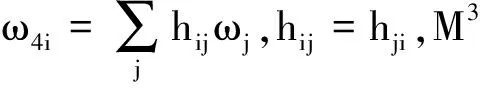
设函数u=ω12(e3),v=e2(logk),显然上式等价于
ei(kj)=(ki-kj)ωij(ej),(k1-k2)ω12(e3)=(k2-k3)ω23(e1)=(k1-k3)ω13(e2).
容易得到
e2(v)=v2-u2,e1(u)=e3(v),e2(u)=2uv,e3(u)=-e1(v),
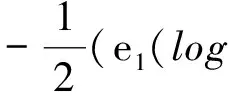
由上式可得
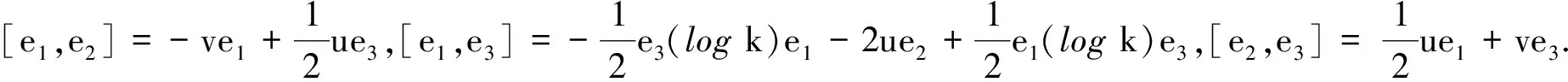
(1)
文献[7]中设Mn是n维完备黎曼流形,n≥2,假设h是Mn中光滑非负函数,满足Δh≥ch2,c≥0是常数,则h恒为零.
2 主要结果
假设M3是单连通的,u和v定义在整个M3上,则u和v是调和函数.事实上,
同理可得Δu=0,利用(1)和Δu=Δv=0得
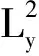
A1e1=0,A1e3=0,A2e1=ke1,A2e3=-ke3.

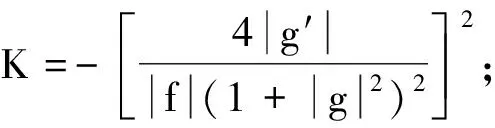
下面通过Weierstrass表示讨论一些例子.
例1[11]f=1,g=-iez,其中z=u+iv,相应的极小曲面为正螺面.
因为ds2=(1+e2u)2(du2+dv2),故(u,v)是等温参数,是正则曲面.在R3中任意紧致集的逆象在(u,v)平面内是紧致的,在(u,v)平面上发散于无穷远的曲线的象在R3中也发散于无穷远,曲面是完备的.
同理,可证明经典的完备极小曲面包括悬链面、Enneper曲面、Scherk曲面、Schwarz曲面等的主曲率都是有界的.
例2为获得Gauss曲率无界的完备极小曲面,考虑Gauss函数[12].设f=1,g=ez2,其中z=rcosθ+irsinθ.
因为ds2=(1+e2r2cos 2θ)2(dr2+r2dθ2),故(r,θ)是等温参数,是正则曲面.在(r,θ)平面上发散于无穷远的曲线的象在R3中也发散于无穷远,曲面是完备的.

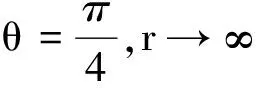
注记更一般地,设f=1,g=ezk,其中k∈Z.高斯曲率为
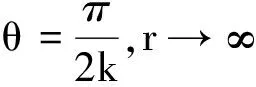
定理2设f:M3→R4是满足Gauss-Kronecker曲率恒为零,第二基本形式恒不为零的等距极小浸入.若M3是完备的,则f(M3)可分解为黎曼直积L2×R,其中L2是R3中高斯曲率有下界的完备极小曲面.
参考文献:
[1] DAJCZER M, GROMOLL D. Gauss parametrizations and rigidity aspects of submanifolds[J]. J Differential Geom, 1985,22(1):1-12.
[2] ALMEIDA S, BRITO F. Minimal hypersurfaces with constant Gauss-Kronecker curvature[J]. Math Z, 1987,195(8):99-107.
[3] ALMEIDA S, BRITO F. Closed hypersurfaces ofS4(1) with two constant symmetric curvature[J]. Ann Fac Sci Toulouse Math, 1997,6(6):187-202.
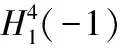
[5] CHENG Q M. Hypersurfaces with constant quasi-Gauss-Kronecker curvature inS4(1)[J]. Adv in Math, 1993,22(2):125-132.
[6] CHENG Q M. Complete space-like submanifolds in a de Sitter space with parallel mean curvature vector[J]. Math Z, 1991,206(3):333-339.
[7] HASANIS T, SAVAS-HALILAJ A, VLACHOS T. Minimal hypersurfaces with zero Gauss-Kronecker curvature[J]. Ill J Math, 2005,49(2):523-529.
[8] HASANIS T, SAVAS-HALILAJ A, VLACHOS T. Complete minimal hypersurfaces in the hyperbolic spaceH4with vanishing Gauss-Kronecker curvature[J]. Trans Am Math Soc, 2007,359(6):2799-2818.
[9] HASANIS T, SAVAS-HALILAJ A, VLACHOS T. Complete minimal hypersurfaces inS4with zero Gauss-Kronecker curvature[J]. Math Proc Camb Philos Soc, 2007,142(1):125-132.
[10] 彭家贵,陈 卿. 微分几何[M]. 北京: 高等教育出版社, 2002.
[11] 忻元龙. 极小曲面的Bernstein型定理与Gauss映照的值分布[J]. 数学进展, 1989,18(4):402-411.
[12] 辛萍芳. 极小曲面的构造[J]. 湖北师范学院自然科学学报, 2002,22(4):31-34.
[13] 吴金文. 数量曲率刻划的球面中紧致极小子流形[J]. 湖南师范大学自然科学学报, 2001,24(2):12-14.
