大型拱坝的地震稳定性分析

［瑞士］ M.维兰德

当接缝处裂缝充分发育时，这些裂缝连接在一起就形成分离的混凝土块。任何进一步的动态变形主要出现在这些裂缝处，从而限制了混凝土块中的拉应力，防止大体积混凝土中进一步产生裂缝。由于拱坝的几何形状受到限制，这些分离的混凝土块只会朝水库方向移动。如果在收缩缝处设置抗剪键，则此类移动将进一步受到限制。

开裂的层间缝由接触单元模拟，混凝土块承受滑移和摆动产生的组合移动。使用间隙单元可以防止大坝下游面以外的分离混凝土块产生任何移动。对收缩缝处的抗剪键所产生的限制作用从保守考虑忽略不计。

提出的方法用在一座250 m高的拱坝上。在水库空库和蓄满两种工况下及在最大可信地震(MCE)产生的地动情况下，对该坝中央上部两个分离的20 m和40 m高的混凝土块的动态稳定性进行了研究。在空库情况下，20 m高的混凝土块最大上游方向滑移距离为105 cm。在发生地震期间和地震后这不可能引起混凝土块倾翻，因为滑移面部位大坝的厚度达到了17 m左右。在更危险(满库)工况下，20 m高的混凝土块的最大滑移位移却明显小很多，只有35 cm左右。

基于大坝水平拱的一个简单模型给出了估算收缩缝开度的近似计算法。该法假定混凝土块的性能就像收缩缝之间的刚体，并假定坝顶所有的径向位移只是收缩缝张开引起的。

1 概述

在对大型拱坝进行线弹性分析时，最大可信地震(MCE)引起强烈地面摇动期间都会出现拉应力大于大体积混凝土的动态抗拉强度。线弹性动态分析是相当直截了当的，尤其是用附加质量表示其与水库的互相作用，并假定坝基无质量时更是如此。

为了证明线弹性分析的有效性，在有限元分析中，常常忽略了大坝与坝基接触处存在的应力集中，收缩缝与层间缝的低抗拉强度特性也被忽视。通过忽略尺度作用、采用断裂模量代替单轴抗拉强度，并利用允许使用的很大的动态抗拉强度值的概念(如视在抗拉强度)来假定大体积混凝土的最有利的动态抗拉强度值。此外，还应用了相当低的地面移动输入值，因为在估算强震引起的地动时存在很大的不确定性。

一旦收缩缝和层间缝张开，裂缝充分发育，则评估拱坝动态稳定性时仍然缺少很清楚的概念。本文给出的分析分离混凝土块动态稳定性的方法包括一条简单的途径，它可以在坝中裂缝充分发育后还能对大型拱坝的安全性进行评估。

2 混凝土坝承受强烈地动的机理分析

用脆性材料(如砖石)建成的建筑物，在受到强烈地面摇动时就会受到严重破坏甚至倒塌。这已经得到证实，如2003年在伊朗巴姆省发生的地震，由于抗剪强度很低的砌体房屋倒塌造成大量居民伤亡。实质上，大体积混凝土受拉时跟砖石砌体一样也是一种很弱的脆性材料，由其浇注而成的混凝土坝，也很容易受到地震的影响。但是，尽管有几座大坝已经承受了峰值地面加速度(PGA)超过其设计值的强烈地面摇动的影响，至今为止没有一座大坝在地震期间溃坝，这表明混凝土坝还有一些砖石建筑物所没有的潜质。

大型混凝土坝能够承受大大超出其设计地动值的地动的根本原因在于它存在某种延展性和“失效保护因素”。大型混凝土坝具有这些特征，原因如下:

(1)混凝土坝的长细比很小，可以使分离的混凝土块在破坏前承受相当大的滑移移动。这种特性可以看成是“几何延展性”。

(2)由于混凝土坝是分块浇注而成，每隔2～3 m设置一个水平层间缝，地震期间大坝应力很大的中央上部形成的任何裂缝可能也是水平的。此外，由于地震加载导致垂直收缩缝张开。稳定性分析表明，形成水平裂缝对混凝土坝的动态稳定性是极为有利的。这类似于在为钢筋混凝土结构进行地震设计时使用的容量设计法中的一个预定失效模式。

沿强度相对较弱的层间缝形成的水平裂缝以及垂直收缩缝的张开将会保护大坝其余部位在发生地震期间不会开裂。在伊朗106 m高的塞菲德鲁德(Sefid Rud)支墩坝上曾观测到这种性状，该坝在1990年6月21日遭受一次接近于MCE的超强地震。该坝也许是迄今为止评估大型混凝土坝非弹性性状最重要的参考实例。尽管大坝上部沿层间缝生成了很多水平裂缝，从大坝上游面扩展到下游面的裂缝处的滑移量实际上是可以忽略不计的。

3 拱坝地震分析法

拱坝地震分析用到的方法有以下几种:

(1)假定水库是不可压缩的(附加质量在大坝上游面)、基岩无质量的大坝-水库-坝基系统线弹性分析法。

(2)考虑了库水压缩性、大坝-基岩有动态相互作用的大坝-水库-坝基系统的线弹性分析法。该法使用了各种先进的非反射边界表达式来模拟水库和基岩外边界处向外的波辐射。但是，鉴于在现有的计算机程序里难以将这样复杂的公式纳入其中，且在大坝地震分析中存在为数众多的不确定性，只有按照Lysmer等人提出的方法通过简单的减震器才能在大多数情况下模拟传递边界。

(3)非弹性动态分析法。该法使用分布裂缝模型在未考虑收缩缝和层间缝的情况下来模拟大体积混凝土。这样的一种方法可用于确定大坝中离散裂缝可能出现的位置。

(4)采用离散法模拟收缩缝的非弹性动态分析法。

(5)采用离散法模拟收缩缝和层间缝的非弹性动态分析法。

(6)采用简单的2D模型模拟遭受摇动和滑动的分离混凝土块的非弹性动态分析法。

使用3D有限元法模拟大坝-水库-坝基系统的方法(1)和方法(2)已经非常成熟和完善;采用分布裂缝法的方法(3)是基于混凝土模型提出来的，需要大量的材料参数，在实际应用中很难获取到这些参数，因此只能根据文献中的数据进行估算。所以，这种方法获得的结果的可信度是相当有限的。此外，分布裂缝的假设也没有得到实际地震观测或实验研究(只出现几条离散裂缝)的支持。用方法(4)和方法(5)对许多拱坝进行了分析研究。

很显然，必须使用考虑了收缩缝张开、层间缝开裂以及坝基处应力集中部位开裂的非弹性分析法才能预测遭受强烈地面摇动的大型拱坝的动态性状。但是，拱坝完全非弹性3D地震分析法仍处于研究之中，尚不能用于常规应用。因此，提出了对分离混凝土块进行简化开裂后分析的方法(6)。下文将对这种方法在对多座大型拱坝进行地震安全性评估中的应用加以介绍。

4 分离混凝土块简化动态稳定性分析法

提出的对拱坝中央上部分离混凝土块进行动态稳定性分析的简化方法包括以下几个步骤:

(1)对大坝-水库-坝基系统进行线弹性动态时程分析，计算动态主拉应力与绝对加速度的包络线(分析可以在空库和满库情况下进行，但是很显然人们对在满库情况下进行地震安全性评估更感兴趣);

(2)根据动态主拉应力与绝对加速度的包络线选择分离的混凝土块进行动态稳定性分析(至少要选择2个或3个由张开的收缩缝和水平层间缝形成的危险混凝土块进行分析研究);

(3)根据分析步骤(1)获得的结果得出每个分离的混凝土块基底处绝对加速度径向和垂直分量的时程曲线;

(4)采用2D有限元模型对分离的混凝土块进行模拟，在这种模拟过程中，开裂的层间缝用接触单元进行模拟(因受到拱坝几何形状限制，也可以利用间隙单元来防止混凝土块滑移到拱坝下游面以外);

(5)根据步骤(3)获得的输入基底加速度对每个分离的混凝土块的摇动-滑动响应进行非线性动态分析;

(6)估算出至少3种不同地动情况下每个分离混凝土块基底上下游边缘处的最大滑移量和最大裂缝张口位移量(高度较小的混凝土块将遭受最大滑移量，因为沿上下游方向的最大地震加速度出现在坝顶);

(7)根据步骤(6)获得的结果对分离的混凝土块的动态稳定性进行评估。

5 动态稳定性简化分析法的假定条件

分离的混凝土块的动态稳定性取决于线弹性大坝-坝基-水库系统的动态响应。除了地震输入之外，控制一座大坝动态响应的最重要的因素是线弹性模型中假设的阻尼水平。对大型拱坝进行环境振动和强迫振动试验结果表明:对于较小振幅的振动，最小模式只能使阻尼比达到1%～5%。对于受到强烈地面摇动影响的拱坝进行地震安全评估而言，即使在考虑非线性作用(如裂缝张开、混凝土开裂以及地震波辐射扩散到水库及基岩)的情况下，假定阻尼比达到5%～10%仍然是谨慎保守的。有时根据理论考虑采用的阻尼比大于10%，但这样高的阻尼比缺乏实测数据的支持。

对分离的混凝土块进行动态稳定性分析所做的其他假定条件还有:

(1)对大坝-坝基-水库系统进行线弹性分析可以计算出收缩缝张开时开裂坝中央上部的加速度响应值;

(2)由于受到拱坝几何形状的限制，分离的混凝土块不可能移到大坝下游面之外;

(3)忽略收缩缝中抗剪键的作用;

(4)裂缝只出现在垂直收缩缝和水平层间缝处，若分离的混凝土块基底有一条向下倾向水库的斜裂缝，预计滑动位移量可能比水平裂缝情况的大很多;

(5)满库时，层间缝中的扬压力呈三角形分布;

(6)根据不可压缩水库的威斯特卡德(Westergaard)理论，水动力附加质量附加到大坝上游面。

6 最大收缩缝张开位移量的估算

收缩缝的张开位移量可以根据用线弹性地震分析获得的径向位移的分布进行估算。计算时，假定混凝土块就像收缩缝之间的刚体，并假定坝顶所有的径向位移都是由收缩缝的张开引起的。每个刚性的混凝土块的转动量约等于其两端的径向位移之差除以混凝土块长度，收缩缝的张开位移量则可以看成是在假定转动点位于大坝下游面的情况下相邻两个混凝土块之间的相对转动量乘以坝顶厚度。

7 实例

使用本文介绍的简化方法，对250 m高的德里内尔(Deriner)拱坝中央上部分离的混凝土块在遭受MCE时的动态稳定性进行了分析，并估算出了收缩缝的最大张开量。为此，先用一个3D模型对大坝-坝基-水库系统进行线弹性分析，然后用2D模型对所选的分离混凝土块进行摇动-滑动分析。这个只有两个步骤的方法比任何完全非线性3D动态分析法都简单得多。全部的动态计算都用计算机程序进行。

7.1 大坝-坝基模型的线弹性分析

用图1所示的有限元模型对大坝进行3D线弹性分析。在占主导地位的振动模态情况下，假定阻尼比为7%。大体积混凝土和岩石的动态弹性模量分别为30 GPA和20 GPa，泊松比分别为0.2和0.3。

用人为产生的频谱一致的加速度时程曲线来表示地震激发的3个分量(见图1)。MCE水平和垂直分量的峰值地面加速度(PGA)分别为0.35 g和0.23 g。使用了统计上独立的3组输入地动值，分别为MCE1，MCE2和MCE3，对应的历时分别为15，25 s和 32 s。

上下游方向的绝对加速度以及线弹性分析获得的动态主拉应力最大值(包络线)的等值线分别如图2和图3所示。

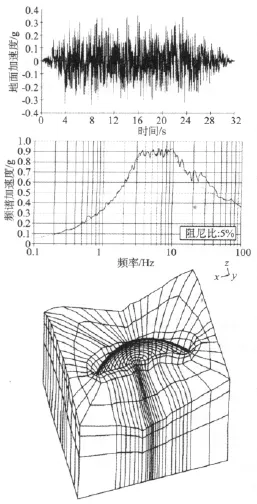
图1 地震输入与3D大坝-坝基模型

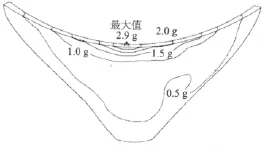
图2 上下游方向水平绝对加速度的包络线

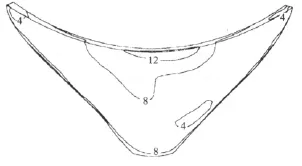
图3 线弹性分析获得的最大动态主拉应力包络线

7.2 分离混凝土块的摇动-滑动分析

在空库和满库条件、上述3种不同输入地动情况下对两个分离的混凝土块(一个高40 m，另外一个高20 m)进行了2D摇动-滑动分析(见图4和图5)。通过改变输入地动符号对每种情况重复进行计算。所以，总共对24种情况进行了研究。假定每个混凝土块基底的滑动摩擦系数为0.7。将摇动中心点向坝体移动大约1 m，以考虑层间缝上下游面处的混凝土剥落(见图5)。

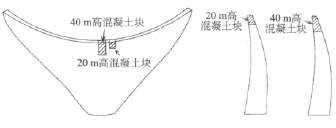
图4 地震稳定性分析所用的2个分离的混凝土块(高度分别为20 m与40 m)

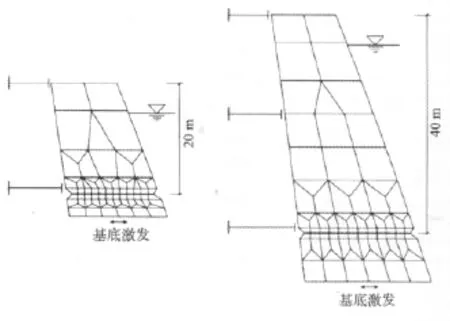
图5 用间隙单元对20，40 m高的分离混凝土块进行的2D模拟

对分离的混凝土块进行摇动-滑动分析获得的结果如表1所示。朝上游面滑移及混凝土块基底下游边裂缝张开位移量典型的时程曲线见图6。20 m高混凝土块的动态响应见图7。

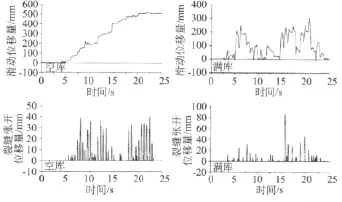
图6 在空库和满库条件下20 m高混凝土块摇动-滑动响应期间朝上游侧滑移及混凝土块下游坝面处边裂缝张开位移量的典型时程曲线

从表1可以看出，最大滑动和摇动位移量的变化都很大，这就是在这样的非弹性分析中要使用几组地震输入值是非常重要的原因;否则，得出的结果就会过于乐观。

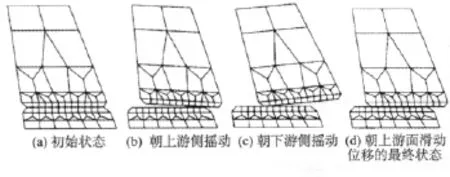
图7 20 m高混凝土块的摇动-滑动移动

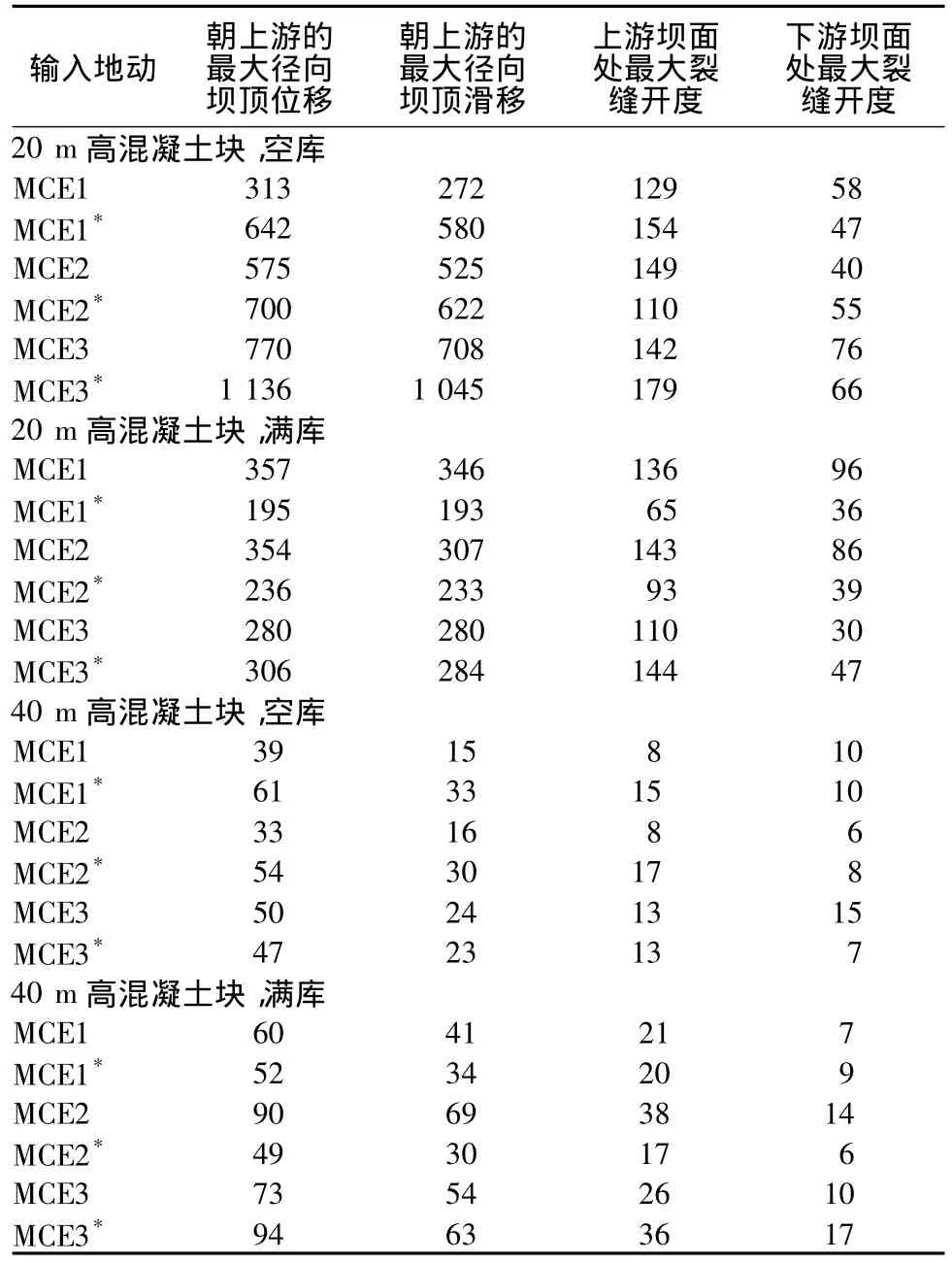
表1 在空库和满库条件下大坝中央上部分离的混凝土块的最大动态响应值mm

在对一个刚体进行摇动-滑动分析时之所以存在数值困难，一是因为滑动移动的粘滑特性使然，二是摇动的混凝土块对下支撑面的冲击产生的冲击力很大。由于这种分析相当棘手，必须通过大量的数值试验来验证结果的一致性和收敛性。计算获得的动态响应对选择的积分时间步长、收敛标准、纽马克积分法使用的参数以及使用约束函数的接触算法的参数很敏感。

7.3 摇动-滑动分析结果讨论

从表1所示的综合性动态稳定性分析结果可以看出以下几点:

(1)空库、满库条件下40 m高混凝土块的最大滑动位移量分别为33 mm和69 mm。在这两种情况下，强烈移动的历时对该混凝土块的最大滑动位移量作用不大;

(2)在满库条件下，40 m高混凝土块基底上游边缘处的最大裂缝张开位移量为38 mm，是下游边缘处最大裂缝张开位移量(17 mm)的2倍。反之，在空库情况下，上下游边缘处最大裂缝张开位移量分别为15 mm和17 mm，该混凝土块基底的最大裂缝张开位移量几乎是相等的。

(3)在满库条件下，20 m高混凝土块向上游测位移了346 mm，强烈地面摇动的历时对该混凝土块的最大滑动位移量作用不大，由于水静压力的恢复作用，该混凝土块有被推回到原来位置的趋势。

(4)空库条件下20 m高混凝土块向上游侧的最大滑动位移量为1045 mm，是满库情况下346 mm的3倍。水平PGA为0.35 g的MCE所引起的滑动位移约为1 m，这种位移量仍然是可以接收的，因为在该混凝土块的基底处坝的厚度达到了17 m左右。

(5)空库条件下地面强烈摇动的历时对20 m高混凝土块的最大滑动位移量作用很大，这与混凝土块的形状不对称有关，导致朝下游的摇动响应比朝上游的摇动响应强烈。由于动态冲击力被摇动和滑动产生的组合移动所分担，朝上游的较小的摇动响应很可能伴随着该方向的较大的滑动响应。因此，朝上游面的滑移具有累积特性。如果混凝土块是对称的(关于垂直面)，就不会有向上游侧滑移的趋势，最终的滑移就有可能相当小。数值模拟验证了这个断言。

(6)在空库条件下，20 m高混凝土块基底上下游边缘处的最大裂缝张开位移量分别为179 mm和76 mm。满库时相应的值分别为144 mm和96 mm。上游侧裂缝开度更大是因为20 m高的混凝土块在满库和空库情况下更容易朝下游摇动。

(7)由于上下游方向的最大加速度响应出现在靠近坝顶的大坝中央上部，20 m高的混凝土块基底比40 m高的混凝土块基底摇动更严重。

因此，20 m高的混凝块经受了明显较大的滑动和摇动位移。

8 最大收缩缝张开度的估算

本文假定拱坝所有的变形只出现在张开缝处计算获得的坝顶垂直收缩缝的最大张开度。为了进行这种近似计算，假定混凝土块就像张开缝之间的刚体。

收缩缝最大张开度可能出现在沿坝顶径向位移曲率最大的位置处。计算了最大径向变位为188 mm时满库情况下由地震引起的收缩缝开度(见图8)。假定了坝顶朝水库位移时大坝上游面处只有一条收缩缝是张开的。

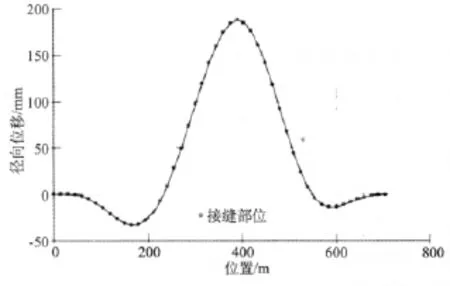
图8 满库情况下坝顶最大径向变位

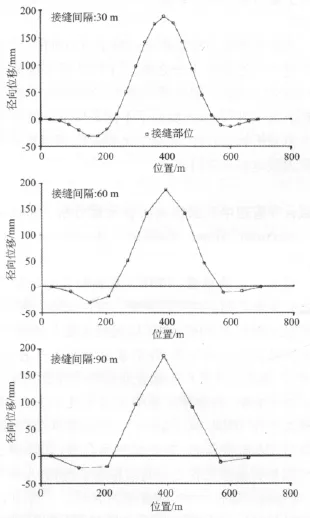
图9 假设坝顶处坝体由间隔30，60，90 m的接缝分开的刚性混凝土块组成情况下地震加荷引起的径向位移(收缩缝处坝体弯折表明相邻混凝土块之间发生相对转动，从而导致接缝张开)

混凝土块宽约15 m。地震期间可能只有几条收缩缝是张开的，其余的都是封闭的。因此，在计算接缝张开度时考虑了多种情况，即采用张开收缩缝之间的间距分别为 15，30，45，60，90 m(见图 9)。

由于顶拱的径向位移图的形式，较大的曲率发生在坝顶中央部位，以及坝肩附近大约1/6点处。因为满库条件下坝顶中央也存在一个朝下游的静变位(约为115 mm)，则朝上游的总静变位与动变位之和为188-115=73 mm。因此，对于坝顶中间部位，为了考虑静变位，必须将表2中的结果按73/188=0.388比例缩小。但是，坝肩1/6点处的水静力位移几乎可以忽略不计，表2中这些点的值不需要作任何调整。

空库条件下，坝顶中央最大动态径向位移为122 mm，因此也要使用表2中的结果乘以一个系数122/188=0.649来估算空库条件下收缩缝的张开位移。

虽然发生地震期间一些止水可能会因为收缩缝的张开而失效，但产生的漏水量是有限的，因为收缩缝张开是暂时性的，较大的接缝开度只出现在水静压力较小的坝顶区。而漏水也可以在震后通过降低库水位来加以控制。

9 结语

提出了一种两步骤方法用于对拱坝中央上部分离的混凝土块进行地震稳定性分析。第1步，用3D模型对大坝-水库-坝基系统进行线弹性动态分析;第2步，将第1步计算获得的可能分离的混凝土块基底处的加速度响应用作输入移动值，以便对混凝土块的摇动-滑动响应进行分析。由于剪切键的作用可以忽略不计，因此可以认为该方法是保守的。

分离的混凝土块，其非弹性动态响应结果对很多数值参数很敏感。因此，必须进行广泛的敏感性检验，以确保获得的结果是可靠的。

重要的是应采用多个统计上独立的输入地震值进行非弹性分析，因为最大滑动位移和摇动位移可能相当分散;否则，获得的结果就会太乐观。

可以根据沿坝顶最大动态径向位移的分布来估算发生地震期间收缩缝的张开度。