工程机械综合传动装置磨损量预测分析

马 凯

（邯郸市高速公路管理处，河北 邯郸 056002）

1 工程车辆综合传动装置的磨损问题

随着工程车辆技术的发展，其传动装置由以往的单纯机械传动系统转变为由机械传动、液力传动、液压传动和其他动力驱动方式以及传感器检测、计算机控制等诸多子系统构成的机电液一体化的复杂传动系统。车辆传动装置也由以往的单纯传递动力转变为集液力变矩器、变速机构、转向机构和制动机构系统于一体的综合传动装置。综合传动装置传递功率密度的增大，使得各摩擦副磨损加剧，进而影响其传动效率和使用寿命。

根据综合传动装置摩擦副磨损机理，可以将其磨损主要划分为四种类型。

1.1 粘着磨损

综合传动装置汇流行星机构由太阳轮、齿圈、行星轮和行星架组成。行星轮在高速自转的同时还在绕太阳轮公转，因此，在行星机构载荷分布不均时，行星轮轴承承受太阳轮啮合力、齿圈啮合力和离心力作用，轴承承受载荷大，润滑条件差，极易发生行星轮轴的粘着磨损。在综合传动过程中，由于啮合齿面温度较高，引起润滑油膜破裂，齿面在一定压力作用下发生直接接触，导致表面膜破坏和齿面粘着；随着齿面的相对运动，部分粘着金属被撕裂，形成两齿面之间表层材料的转移，这种齿面损伤易成为齿面胶合。

1.2 磨粒磨损

两个接触表面之间由于坚硬的凸起或微粒造成摩擦过程中表面材料的移动和脱落称为磨料磨损。它是一种最常见也最严重的磨损形式。磨料磨损的机理是比较简单的，实际上就是磨粒的犁沟作业，即微观切削过程。不同的磨料磨损工况会产生不同类型的切屑状颗粒，综合传动装置磨合过程油液中存在有粗大并有褶皱的二体磨料磨损颗粒和细长状钢质三体磨料磨损颗粒。

1.3 疲劳磨损

疲劳磨损一般发生在润滑条件较好的闭式机械系统中，综合传动装置一轴、二轴、三轴、输入轴和轴承零件磨损多属于疲劳磨损失效形式。

齿面点蚀是工作齿面在接触应力的长期反复作用下，其表面金属小块疲劳脱落的一种齿面失效形式。在滚滑运动中，接触表面在相对滑动时引起初始裂纹，当两齿面相互滚动时，接触面上的裂纹将因润滑油被挤入裂缝中而使裂纹逐渐扩展，当裂纹扩展到一定程度时，即形成小块剥落，这就是点蚀。

综合传动装置螺旋伞齿轮长期在重载工况下工作，齿面上很容易形成点蚀。在交变载荷作用下，滚动轴承滚动体或滚到表面容易发生疲劳剥落或脱皮。

1.4 腐蚀磨损

在综合传动装置各轴承滚动体和滚道的接触处以及与轴的紧固连接处，会发生锈蚀和磨损小坑现象，这种磨损现象属于“微动磨损”，也叫摩擦锈蚀或假形布氏效应（False Branding），其形成犹如布氏硬度剂的压头在金属表面所生成的压痕，所不同的是其凹坑呈现出灰暗、粗糙的形态，而不像真正的布氏压痕那么光洁。综合传动装置的微动磨损更多的是发生在轴承外圈与轴承座或内圈与轴颈的配合处。

2 灰色神经网络模型

所谓灰色神经网络就是将灰色系统方法与神经网络方法有机地结合起来，对复杂的不确定性问题进行求解所建立的模型。

本文将灰色预测模型与神经网络相结合组成串联型灰色神经网络（如图1所示）。

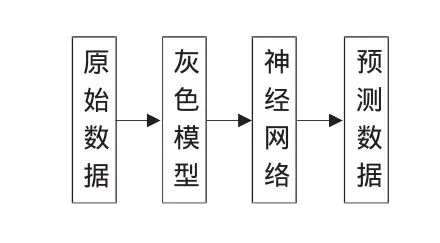
图1 串联型灰色神经网络模型

串联型灰色神经网络模型不但能充分发挥灰色模型和神经网络的优点，而且在模型建立上也比较简单。对于串联型灰色神经网络模型，原始数据输入灰色模型得到预测结果，将预测结果输入训练好的神经网络就得到最终的组合预测结果。其中，神经网络的训练样本为原始数据及其灰色预测值。

考虑到综合传动装置油液分析数据的特殊性，本文所建灰色神经网络模型工作流程如图2所示。

图2中，灰色预测模型采用适合综合传动装置油液分析数据的非等间距GM（1，1）模型，拟合数据序列P与原始数据序列T做为神经网络的输入和输出样本，数据归一化处理采用以下式（1）、式（2）所述的方法，数据还原同样为式（1）、式（2）的逆过程。将非等间距模型预测的下一时刻预测值输入训练好的BP神经网络即可得到最终的预测值。

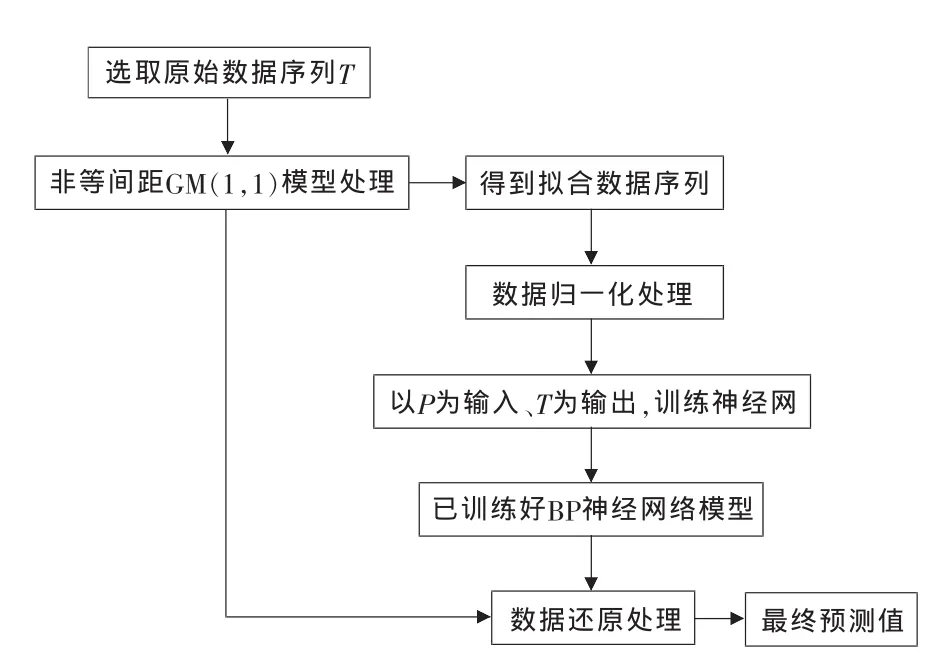
图2 灰色神经网络模型工作流程

3 综合传动装置磨损量预测模型

3.1 模型的选取

综合传动装置油液中Fe元素浓度表征整体磨损状况；Cu元素、Pb元素浓度表征换挡离合器磨损状况；Cr元素、Ni元素浓度表征齿轮类摩擦副磨损状况；Mo元素、Si元素浓度表征铸铁密封环磨损状况；Al元素浓度表征箱体磨损状况。在油液分析所得数据中，取样时间不均匀，每种元素浓度都各不相同，要对元素浓度含量进行预测，就要选取一种鲁棒性较好的模型，时序拟合型灰色神经网络模型受时序波动影响较小，且拟合预测精度较高，因此，本文选用的时序拟合型灰色神经网络模型对综合传动装置磨损量进行预测。

3.2 模型精度检验

灰色模型的主要用途是进行预测，只有通过检验的模型才能用来预测。灰色预测模型精度检验方法一般有三种：

a）残差检验 以模型计算值与原始值之差来检验每个拟合值与原始值的接近程度，是一种直观的算术检验方法；

b）关联度检验 检验两条函数曲线（即原始序列曲线与模型计算数据模拟曲线）的几何形状相似性与接近度；

c）后验差检验 该检验是按残差分布统计特征来检验的一种方法，是能反映出拟合度好坏的一种统计规律。在以上三种检验法中，常用的是后验差检验法。设原始数据序列为x（0），相应的模型模拟序列为，则残差序列ε为：

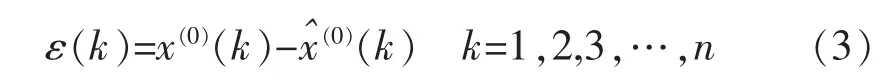
原始数据序列x（0）的均值、方差计算如下：

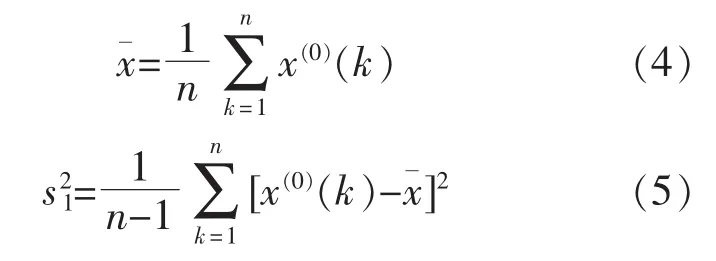
残差序列ε的均值、方差计算如下：

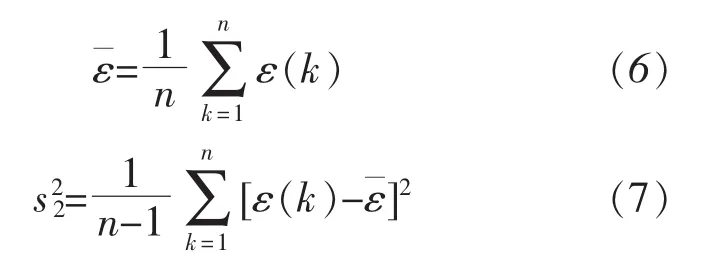
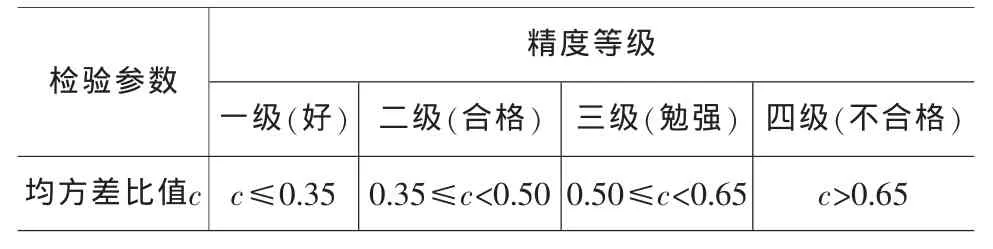
表1 模型精度等级判别

这里对磨损量预测的实例分析过程中，采用后验差检验法对预测结果进行评估。

4 综合传动装置磨损量预测实例分析

某工程机械A的综合传动装置道路试验数据如表2所示。

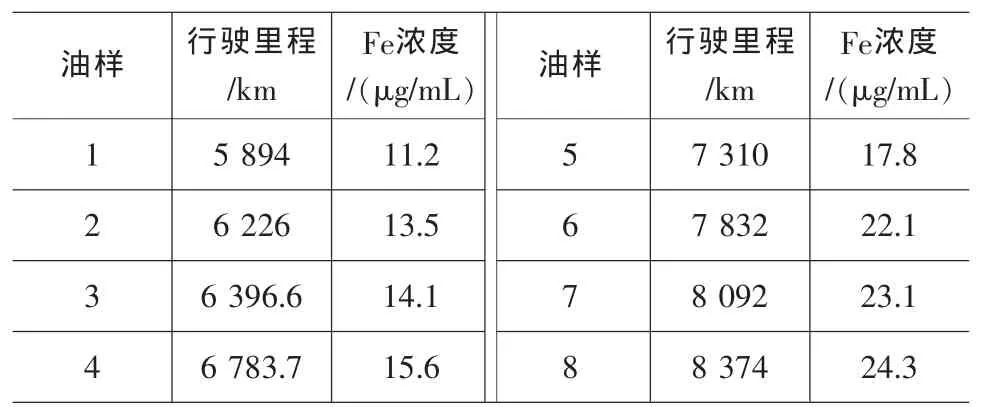
表2 某工程机械A的综合传动装置道路试验数据

下面以表2中数据为例，应用时序拟合型灰色神经网络模型对未知行驶里程的Fe浓度进行预测。预测之前需要对模型的拟合精度进行后验差法检验。

考虑数据的光滑性，首先判断原始数据的级比，即后一个数据与前一个数据的比值，级比上限为，下限为。转化后数据级比若满足要求，则对转化后的数据应用时序拟合型灰色神经网络模型进行拟合。下面对模型拟合精度进行检验，结果如表3所示。

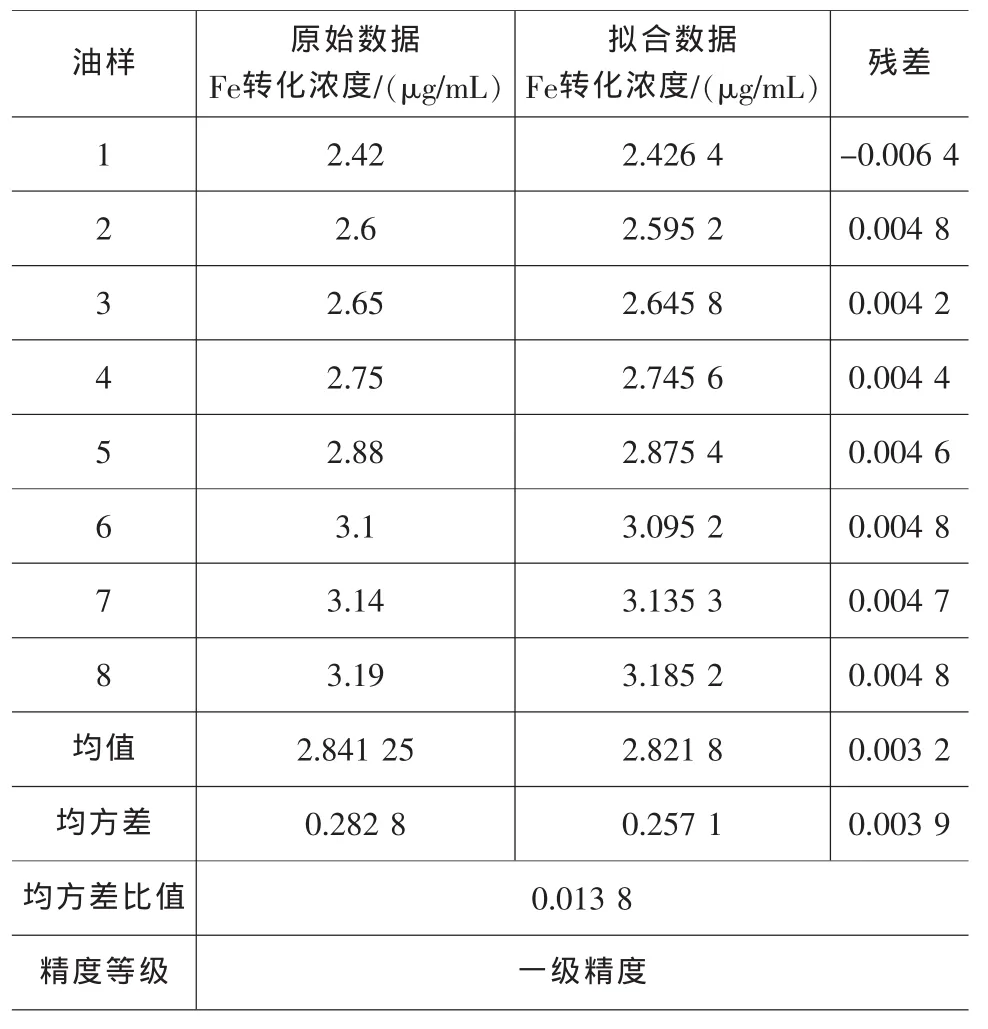
表3 模型精度判断

从表3可以看出，应用灰色神经网络模型完全可以达到拟合精度要求，因此，可以对磨损量进行预测。下面就采用上述模型对后续试验磨损量进行预测，所得结果与原始数据比较如表4所示。

表4 工程机械A的原始数据与预测结果比较

从以上结果可以看出，时序拟合型非等间距灰色模型与神经网络模型组合后的预测模型，预测误差小，能达到较高的预测精度。

为了进一步说明灰色神经网络模型预测的准确性，下面对另一台工程机械B的综合传动装置试验数据进行磨损量预测，原始数据如表5所示。

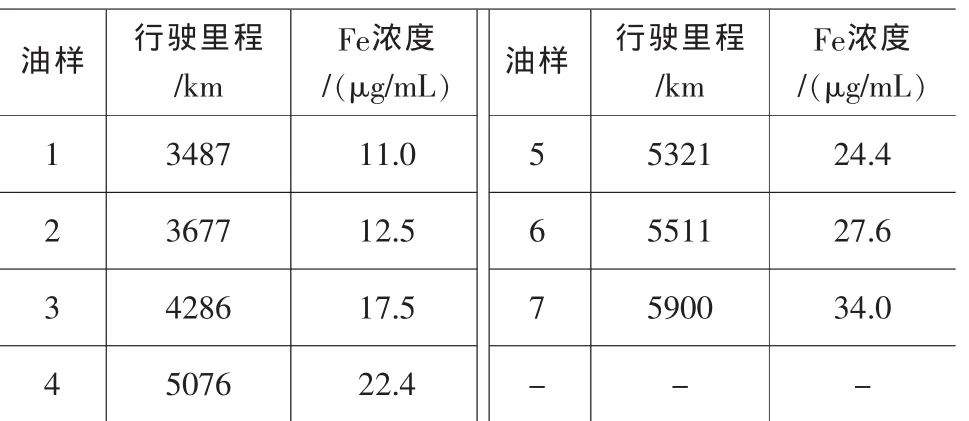
表5 某工程机械B的综合传动装置道路试验数据

根据表5的7个实测数据，预测6 176km处的Fe元素浓度值，并在运行到6 176km时实际进行采样，得到了如表6所示的实际采样结果和预测结果。

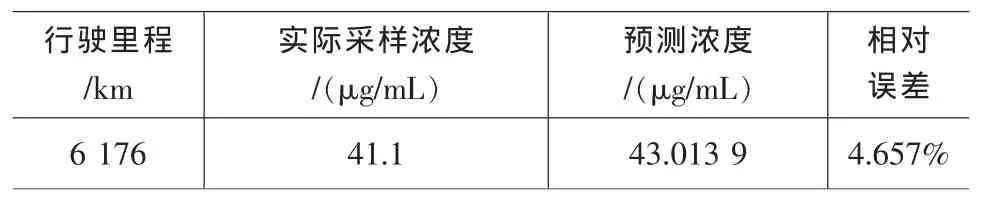
表6 工程机械B的原始数据与预测结果比较

结果表明，时序拟合型灰色神经网络模型预测误差小，预测准确度高。得到良好的预测值之后，就可以判断综合传动装置主要部件磨损状况的发展趋势，从而为故障预测提供了参考依据。

5 结语

本文对综合传动装置磨损元素浓度的预测是针对油液分析数据，而在实际的数据采样过程中，往往存在不确定的干扰因素，使所得数据不够准确。为了更好地掌握真实的数据规律，需要在应用预测方法前对原始数据进行处理，因此，为了减小预测误差，数据预先处理方面的工作还有待进一步研究。

[1]张红，龚玉.磨损趋势预测的GM模型应用[J].机械设计与研究，2001，17（1）：69-71.

[2]王作雷，蔡国梁.非等间距序列建模过程中存在的问题及改进[J].大学数学.2003，19（2）：46-50.

[3]罗佑新，周继荣.非等间距GM（1，1）模型及其在疲劳试验数据处理和疲劳试验在线监测的应用[J].机械强度，1996，18（3）：60-63.

[4]张红，李柱国，陈兆能.非等间距GM模型及其在柴油机磨合试验数据中的应用[J].润滑与密封.2002，1（1）：19-24.