基于高次最小二乘原理的连续刚构桥挠曲线拟合分析

刘大洋，黄福伟，2，禹 鹏

（1.重庆交通大学土木建筑学院，重庆 400074；2.重庆交通科研设计院，重庆 400067）

0 引言

近年来，我国桥梁建设事业迅猛发展，在新建高速公路、高速铁路中桥梁和隧道所占比例逐渐增加。杭州湾跨海大桥，胶州湾跨海大桥也进入正式运营阶段。掌握这些大桥在运营阶段所处的健康状态，对整个桥梁结构的安全具有重要意义。20世纪90年代以来，一些大桥逐步建立了相关的桥梁健康监测系统，如香港青马大桥、江苏润扬大桥、重庆大佛寺长江桥等。

目前在桥梁智能健康监测中，测量桥梁几何线型所需设备主要有全球定位装置，可以转化电信号进入自动化数据采集系统的直流差位移传感器，然而要获得整个桥梁的几何线型，在全桥都安装位移传感器和相关数据采集系统显然是不合理、不科学的。首先是监测的成本增加，其次使得采集系统庞大而复杂。为了有效利用有限的传感器，解决方法主要有以下两个方面：

a）对于优化传感器在桥梁结构的布置，目前有不少人员在这一方面进行了大量的研究，研究方法主要有遗传算法、有效独立法、神经网络法等，取得大量成果，并应用于工程实践[1]；b）用有限的测点信息有效拟合全桥的监测数据也非常重要，但是目前这一方面的研究较少[2]。本文以连续刚构桥为研究桥型，以高次最小二乘原理为分析方法。对某连续刚构桥的边跨和1/2中跨的挠曲线方程进行拟合分析。

1 分析原理

1.1 挠曲线方程分析

在公路桥梁中，汽车活载所占的总荷载的比例较小，影响梁长期变形的荷载主要有桥梁结构本身的自重，桥面铺装、栏杆等二期恒载，在本文中将以上荷载等效为均布荷载q，根据挠曲线方程有[3]：

式中：EI——全桥截面刚度；

ω″（x）——挠曲线方程二阶导数；

M（x）——弯矩方程。

（1）式经两次积分得：

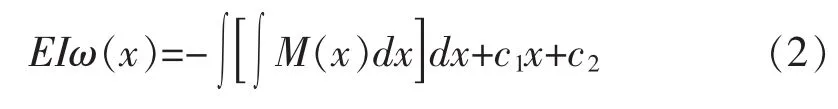
式中：c1、c2——积分常数

式中，M（x）在均布荷载作用下是关于x的二次表达式。综上分析，在均布荷载作用下挠曲线方程是关于x的四次表达式。设挠曲线方程为：

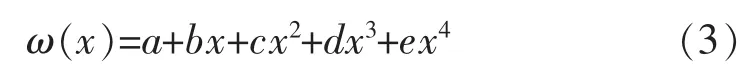
1.2 拟合方法分析

最初挠曲线方程拟合采用牛顿插商法，牛顿插商法虽然不需要各测点的一阶导数和二阶导数，但是通过试算表明，在外插某一点和整个挠曲线时，出现明显误差甚至不收敛现象。如采用样条插值法，需要知道各测点的一阶导数和二阶导数，但在实际工程中这点很难实现。比较分析，最终选用高次最小二乘原理拟合连续刚构桥挠曲线方程。

由前面1.1节挠曲线方程分析中得知挠曲线是关于x的四次多项式，所以采用四次最小二乘原理拟合多项式拟合挠曲线方程。求最小二乘解得一般步骤如下[4]：

a）先根据φ（x）的特点，建立确定ak（k=1，2，3，…，n）的正规方程组；

b）然后通过解正规方程组求取最小二乘解φ*（x）对应的ak*（k=1，2，3，…，n）；

具体计算方法如下，设拟合挠曲线方程：

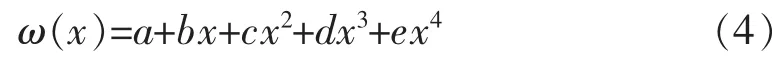
即有φ0（x）=1；φ1（x）=x；φ2（x）=x2；φ3（x）=x3；φ4（x）=x4，相应的正规方程组为：

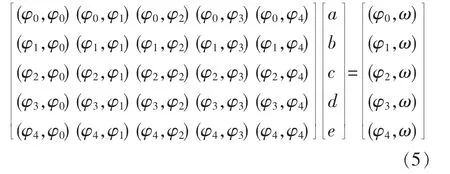
代入测点数据，求解对应的系数，对于实际工程中较多的数据，可用Excel编写简单程序求解。

2 算例分析

2.1 算例简介

某高速公路三跨预应力混凝土连续刚构桥，跨度为110m+200m+110m，采用C50混凝土，左右幅梁体均为单箱单室箱型截面梁，顶板宽13.4m，底板宽7m；根部梁高11.5m，跨中及边跨端直线梁高3.5m；其余梁高按1.5次抛物线变化，顶板最小厚度0.32m；腹板厚度0.6m，0.7m，0.95m不等；底板厚度根部1.2m，跨中及边跨直线段为0.32m。

2.2 算例分析方法

首先通过有限元软件Midas建立全桥模型，定义时间依存性材料与边界条件，输入预应力钢束及预应力荷载，以及自重、二期恒载等。以3年后全桥各节点挠度为基准，用模型计算结果模拟实测值。验算高次最小二乘原理拟合挠曲线的准确性，计算相对误差并分析误差产生原因。

2.3 测点布置

由于全桥为对称结构，算例中只对边跨与1/2中跨的挠曲线进行拟合，边跨分为1/4段与2/4～4/4段两次拟合，1/2中跨一次拟合。模拟实测值为模型中节段的两端节点，测点不可能都刚好位于节段端点，所以实际测点取为距理想测点最近的节点。

经建模计算与实际工程分析，预应力刚构桥在边跨1/4段内底板布置有较多预应力钢束，而在边跨1/4段内的弯矩比较小，加之混凝土的收缩徐变，使得在边跨1/4段梁体出现明显上拱，变形较为复杂。为了满足挠曲线拟合的准确性，将边跨1/4段的挠曲线进行单独拟合，边跨1/4段布置5个均匀分布的测点。

边跨2/4～4/4段测点布置，由于在靠近边跨1/4段和边墩附近的变形较为复杂，所以在边跨2/4～4/4段内测点未采用均匀布置，而是从边跨到边墩按2∶3∶3∶2的距离比布置5个测点，使得在靠近边跨1/4段和边墩附近的测点较密。

中跨测点布置为0/8中跨、1/8中跨、2/8中跨、3/8中跨、4/8中跨。

2.4 数据拟合处理

2.4.1 边跨及1/2中跨的挠度实测值如表1所示。

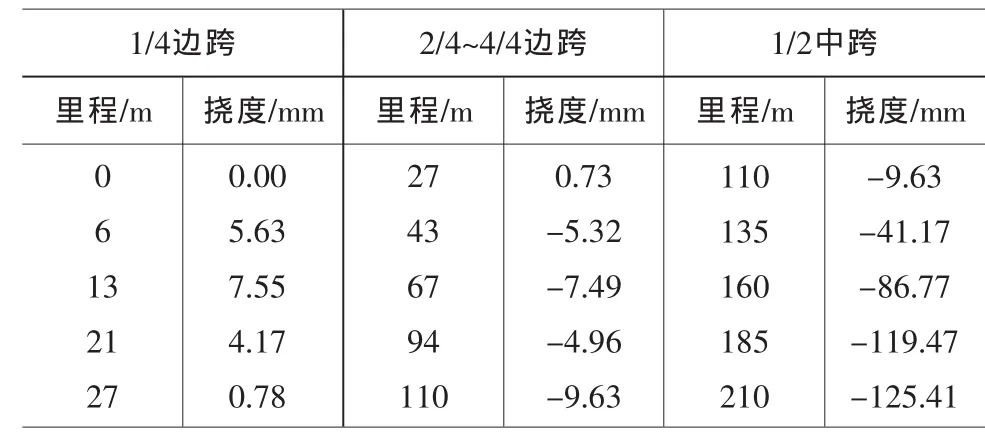
表1 桥梁的实测挠度值

2.4.2 按照1.2节方法求解边跨1/4段挠曲线方程，设边跨挠曲线方程：

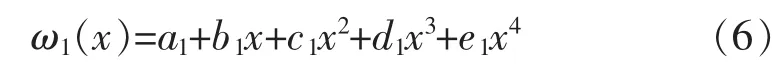
代入建立正规方程组（5）式，求解结果：a1=1.20×10-10；b1=1.17；c1=-2.88×10-2；d1=-2.01×10-3；e1=5.58×10-5

最终边跨挠曲线方程拟合结果：

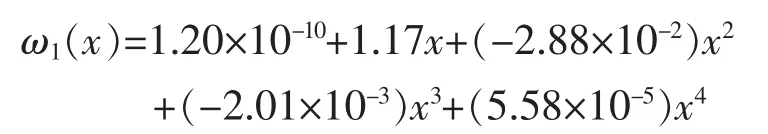
2.4.3 按照1.2节方法求解边跨2/4～4/4段挠曲线方程，设边跨2/4～4/4段挠曲线方程：

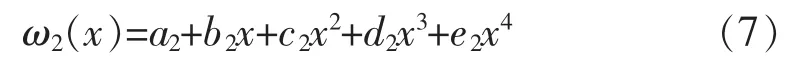
同理代入正规方程组，求解结果：a2=1.17×101；b2=-1.83×10-1；c2=-1.57×10-2；d2=3.19×10-4；e2=-1.61×10-6

最终边跨2/4～4/4段挠曲线方程拟合结果：

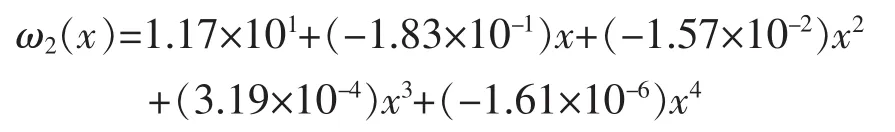
2.4.4 按照1.2节方法求解1/2中跨挠曲线方程，设1/2中跨挠曲线方程：

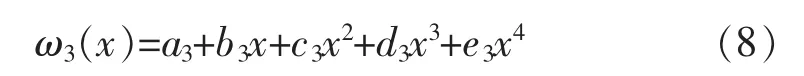
同理代入正规方程组，求解结果：a3=-1.34×103；b3=3.43×101；c3=-3.08×10-1；d3=1.11×10-3；e3=-1.40×10-6

最终1/2中跨挠曲线方程拟合结果：

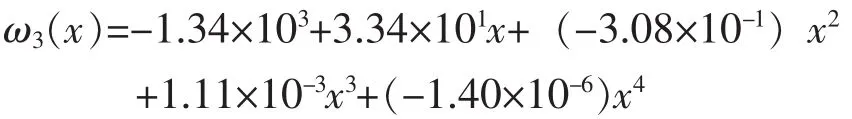
2.5 数据分析

由2.4节边跨挠曲线方程，计算输出边跨1/4段各节点的四次最小二乘原理挠曲线拟合值，并与实测值进行误差分析，边跨1/4段的实测挠度值与四次最小二乘原理拟合挠度值分析如表2所示。

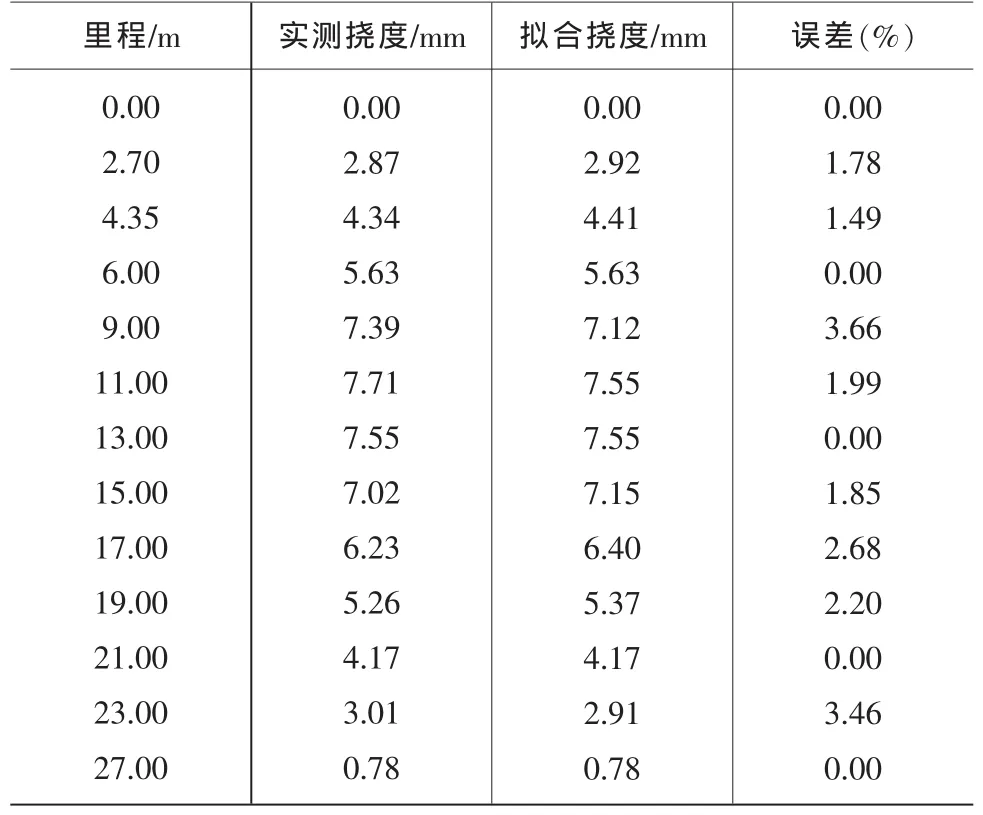
表2 边跨1/4段实测挠度值与拟合挠度值分析

由上表可见边跨1/4段内拟合挠度值与实测挠度值的最大相对误差为3.66%，挠曲线拟合结果的相对误差均小于5%，表明高次最小二乘原理拟合连续刚构桥边跨1/4段挠曲线结果具有足够精度。

边跨1/4段的实测挠度值与四次最小二乘原理拟合挠度值分析如图1所示。

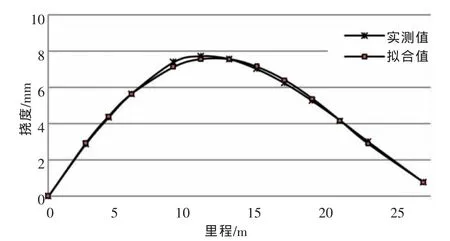
图1 边跨1/4段的实测挠度值与拟合挠度值分析

由2.4节边跨2/4～4/4段挠曲线方程，计算输出边跨2/4～4/4各节点的四次最小二乘原理挠曲线拟合值，并与实测值进行误差分析，边跨2/4～4/4段的实测挠度值与四次最小二乘原理拟合挠度值分析如表3所示。

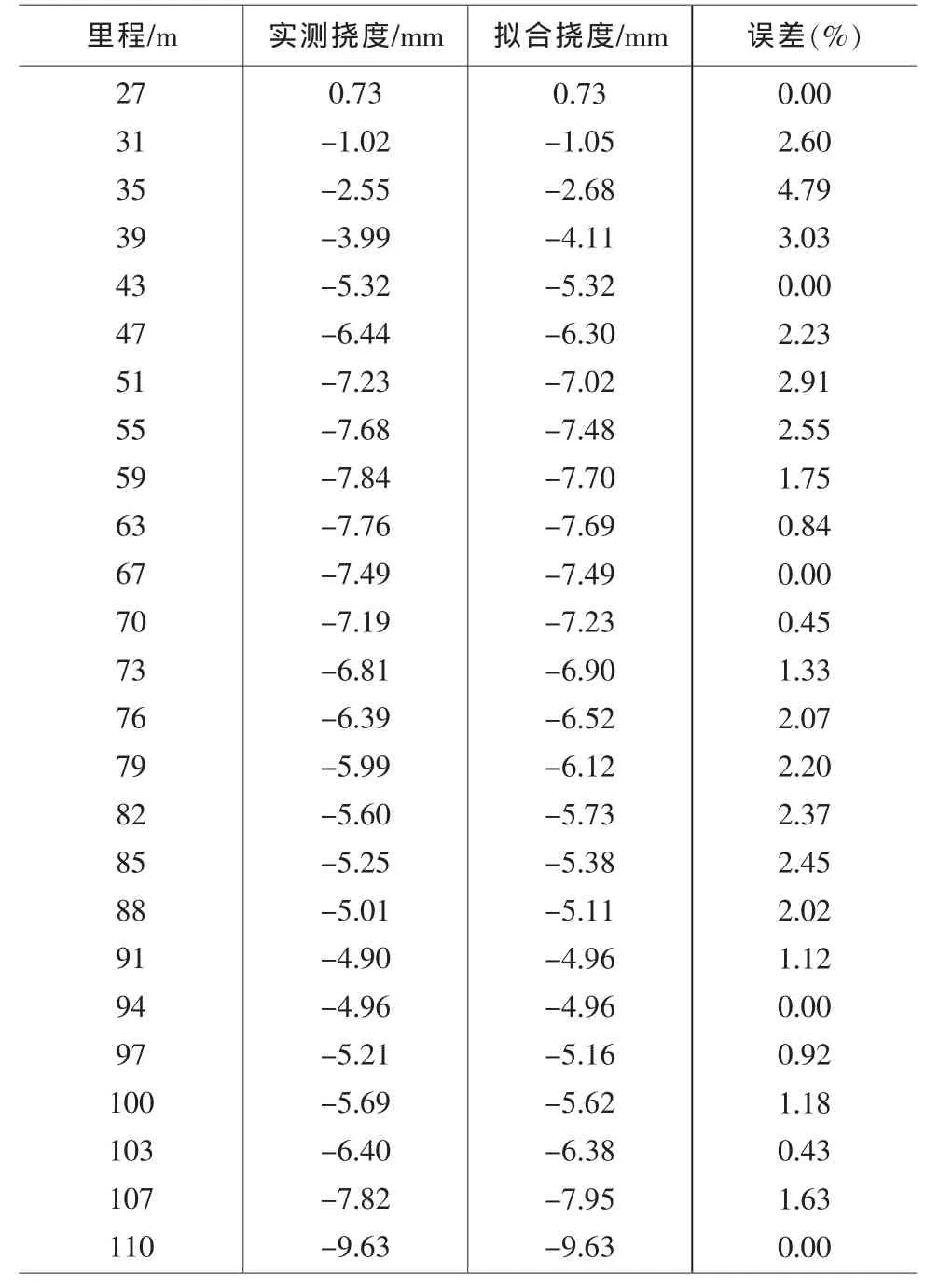
表3 边跨2/4～4/4段实测挠度值与拟合挠度值分析

由表3可见边跨2/4～4/4段内拟合挠度值与实测挠度值的最大相对误差为4.79%，挠曲线拟合结果的相对误差均小于5%，表明高次最小二乘原理拟合连续刚构桥边跨2/4～4/4段挠曲线结果具有足够精度，可满足实际工程需要。

边跨2/4～4/4段的实测挠度值与四次最小二乘原理拟合挠度值分析如图2所示。

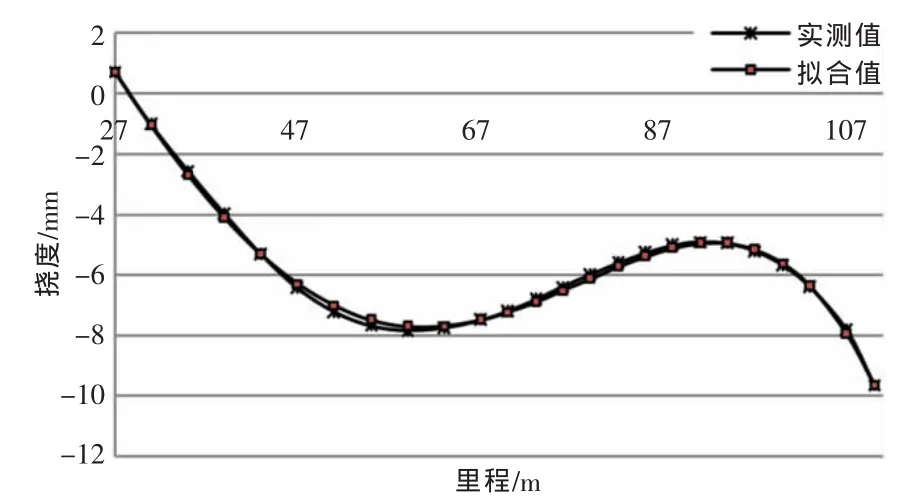
图2 边跨2/4～4/4段的实测挠度值与拟合挠度值分析

由2.4节1/2中跨挠曲线方程，计算输出1/2中跨各节点的四次最小二乘原理拟合挠度值，与实测挠度值进行误差分析，1/2中跨的实测挠度值与四次最小二乘原理拟合挠度值分析如表4所示。

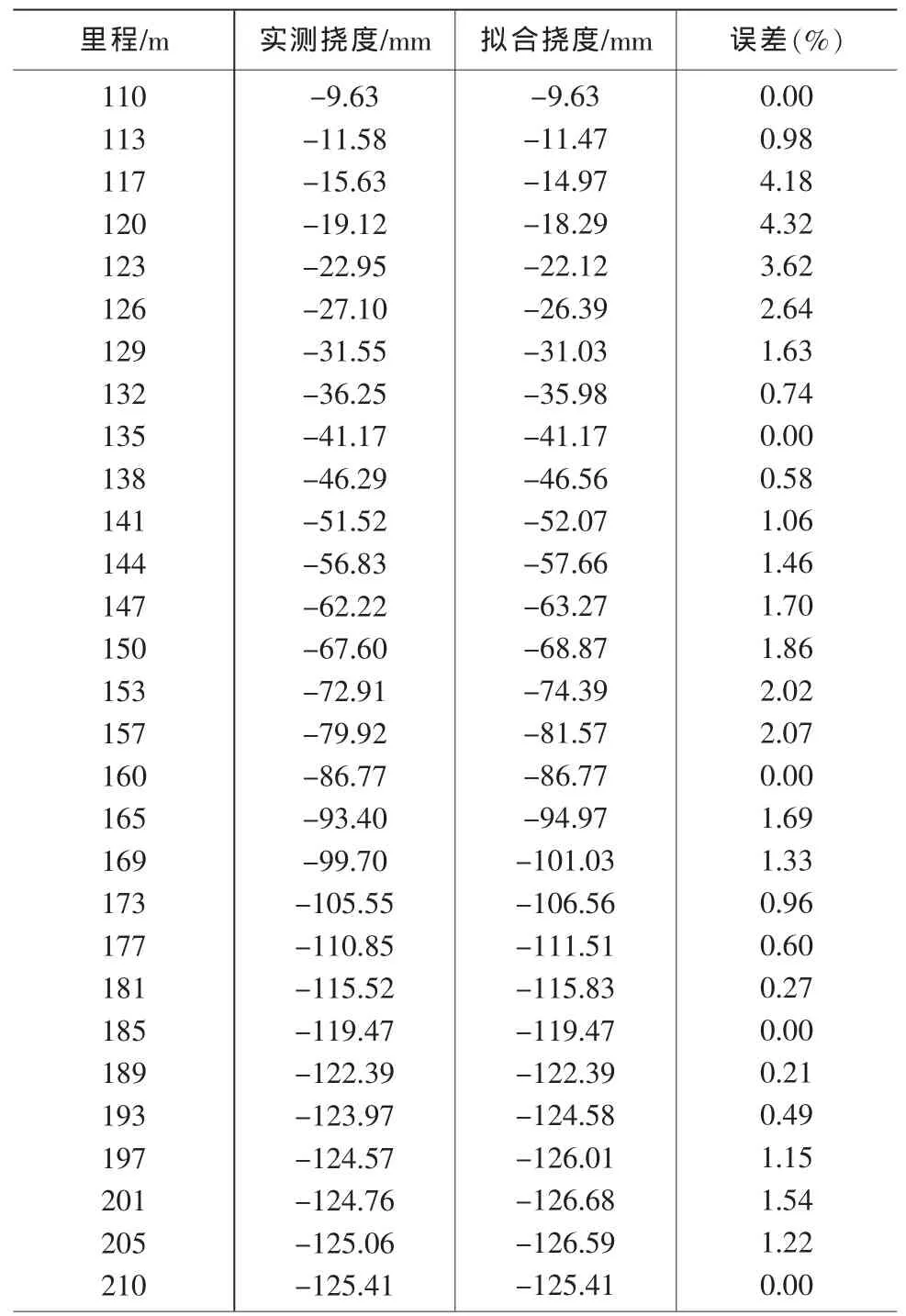
表4 1/2中跨段实测挠度值与拟合挠度值分析

由表4可见1/2中跨内拟合挠度值与实测挠度值的最大相对误差为4.32%，挠曲线拟合结果的相对误差均小于5%，表明高次最小二乘原理拟合连续刚构桥1/2中跨挠曲线结果具有足够精度，可满足实际工程需要。

1/2中跨的实测挠度值与四次最小二乘原理拟合挠度值分析如图3所示。

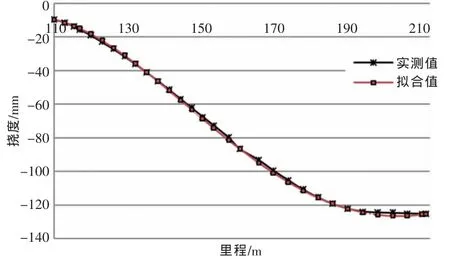
图3 1/2中跨的实测挠度值与拟合挠度值分析

在边跨1/4段内、边跨2/4～4/4段内，以及在1/2中跨挠曲线拟合结果与实测结果的最大相对误差均4.79%，均小于5%。

3 结论

考虑桥梁健康监测的经济成本和便利性，用有限的测点挠度值拟合全桥的挠曲线方程有重要意义，通过以上算例，可以得出以下结论：

a）相对于其它拟合方法，高次最小二乘原理拟合挠曲线方程具有方法简单、思路清晰的优点，有利于工程实践，其不仅适用于连续刚构桥挠曲线的挠曲线拟合，可推广到其它梁式桥的挠曲线拟合；

b）算例分析结果在边跨1/4段内拟合值与实测值的最大相对误差为3.66%，在边跨2/4～4/4段内拟合值与实测值的最大相对误差为4.79%，在1/2中跨内拟合值与实测值的最大相对误差为4.36%，各段内的挠曲线拟合的相对误差均小于5%，表明高次最小二乘原理拟合连续刚构桥挠曲线结果具有足够精度，满足实际工程需要。

[1]黄民水，朱宏平，李炜明.基于改进遗传算法的桥梁结构传感器优化布置[J].振动与冲击，2008，27（3）：82-86.

[2]杨学山，侯兴民，等.桥梁挠度测量的一种新方法[J].土木工程学报，2002，35（2）：92-96.

[3]江晓禹，龚晖.材料力学[M].成都：西南交通大学出版社，2009.

[4]颜庆津.数值分析[M].北京：北京航空航天大学出版社，2010.