寒区隧道气温对隧道温度场的影响分析

2013-11-20李铁根

交通运输研究 2013年24期

李铁根

（兰州交通大学土木工程学院，甘肃兰州 730070）

0 引言

我国已建的寒冷地区隧道很多都发生衬砌开裂、路面冒水、结冰等病害，这大大弱化了隧道的使用功能，严重威胁着行车安全。寒冷地区的公路、铁路隧道和欧美日等国寒冷地区的公路、铁路隧道的使用情况看，冻害现象十分严重，甚至出现因严重冻害而导致隧道主体结构报废和运营期间发生重大交通安全事故。随着我国交通事业的快速发展，在西部的高海拔和北部的高纬度寒冷地区将陆续有大量的隧道建成，与以往寒冷地区的隧道相比，这些隧道的规模会更大、技术要求更高，而气候条件却更加恶劣。在与一般地区相比，寒冷地区修建隧道工程，技术性问题要复杂得多，最主要的问题是寒区隧道一般要受到季节性冻融、冻胀作用影响，这种周期性的加载卸载作用将对隧道主体结构尤其是洞口带的结构造成破坏，进而影响运营期间的安全性及结构的寿命。

1 控制微分方程及其有限元公式

由地壳温度场的知识可知，一般隧道均处于年恒温带或增温带中，即处于稳定温度场中。在隧道开挖后，由于隧道内流动空气与外界交换，使得隧道外周一定范围内围岩温度受隧道环境大气温度的影响，由原来的恒温带或增温带（稳定温度场）转换为变温带（非稳定温度场），如图1[1]所示。

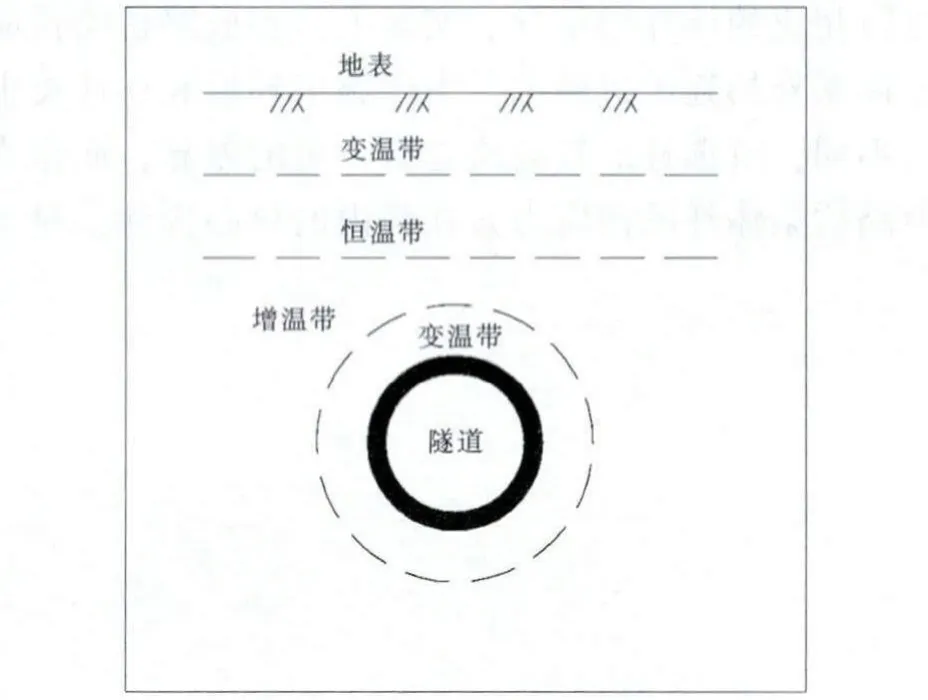
图1 隧道围岩温度场示意图

根据岩体的热传导微分方程：

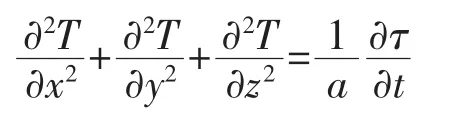
由于隧道腔体的半径较大，可以当作平壁的导热问题来考虑，温度的分布为深度和时间的函数，即为T（z，t），那么此问题的数学表达式为：

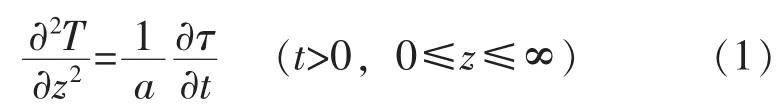
隧道施工后，围岩与外界的热交换过程已持续了很长时间，原有的温度分布已失去了对当前围岩热过程的影响，同时，也无法准确地确定围岩初始状态的温度场，故在讨论的问题中，初始状态失去了它的意义。该问题属于准稳态的热波问题，边界条件为：

因为隧道外的大气温度是呈周期性变化的，那么边界条件式（2）中的衬砌表面温度受外界气温影响也按周期性变化，则f（t）可以表示为傅里叶级数形式，即：

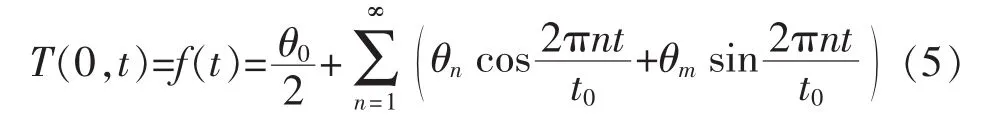
式中：t0——表面温度变化周期；

θ0——t0期间的平均温度；

θn、 θm——分波的振幅，

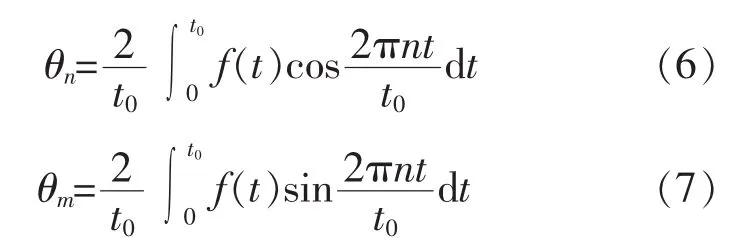
求解（5）的微分方程，可得以下解：

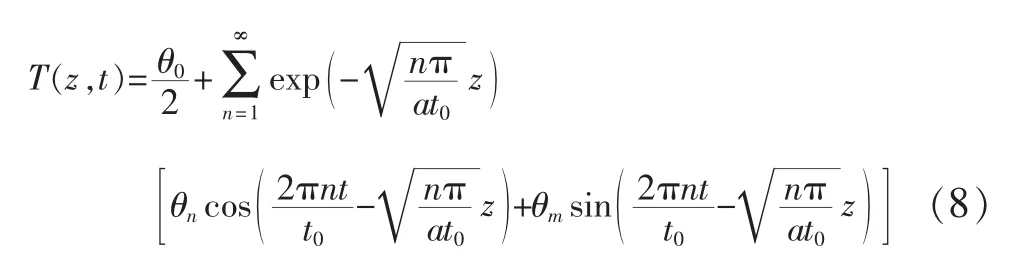
式（8）即为微分方程（1）在边界条件（2）情况下的解，即隧道围岩受隧道内周期变化的气温影响时，任意点z在任意时刻t的温度分布。由于该解为级数形式，实际运用很不方便，且不易直观地看出隧道围岩温度场分布的规律，因此有必要对隧道围岩温度分布解进行简化。

如果对隧道内气温变化规律进行简化，认为其以简谐函数周期性变化，且假设隧道衬砌表面平均温度与该位置洞内气温近似相等，不考虑相位影响，则衬砌表面的温度可以表示为：

式中：T0——衬砌表面的平均温度；

A——衬砌表面的振幅；

t0——振动的周期，可按昼夜，也可按年计算。

在式（2）～（4）的条件下，求解式（1）所示的偏微分方程，根据所讨论的问题物理意义去掉不合适的解，最终求得对应于上述边界条件的解为：

由式（10）可知隧道围岩的温度场分布规律如下：

b）温度波向z的正方向行进，则波的前进速度u和波长l分别由下式计算：

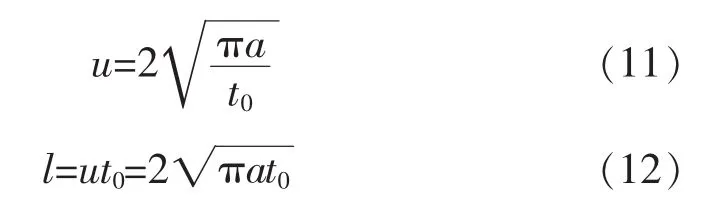
由式（11）可以看出，温度波的传播速度u正比于a的平方根，说明温度波的传播速度与组成围岩的岩石或土壤的导温系数a有密切关系：导温系数a越大，则传播速度越快，a越小，则传播速度越慢。

由式（12）可以看出，温度波的波长除与导温系数有关外，还与周期的平方根成正比，长周期性的温度变化比短周期的温度变化影响深度要大一些。

2 工程概况及理论分析

吐库二线中天山隧道位于托克逊、和硕间中天山东段的岭脊地区，全长22.449km，隧道进口标高1 105m，隧道范围内地层岩性及地下水情况复杂，且为全线的控制工程。进口端根据托克逊气象站多年资料，年平均气温14.5℃，极端最高气温49℃，极端最低气温-25℃，隧道岩层主要为未风化的大理岩。

根据试验数据得到围岩的导热系数λ＝3.13（W·（m·℃）-1），围岩密度ρ＝2900（kg·m-3），围岩的比热C＝1（kJ·（kg·℃）-1）。本次只考虑裸岩中温度的传播情况，未考虑初期支护及二次衬砌在温度传播中的影响。

将温度初始边界条件设置如下：

a）在未考虑洞内温度对模型影响的条件下，将地表温度函数设置为T＝4.5＋37sin（2×3.14／365×I），模型下边届温度按照低温梯度增温率为3℃／100m，计算下边界温度为5.45℃，地表温度函数由中天山隧道冻土围岩的初始地温（通过实地地温观测取值）拟合得到，其中I为计算天数；

b）在考虑洞内温度对模型影响的条件下，将地表及开挖的裸岩温度均设置为T＝4.5＋37sin（2×3.14／365×I），下边界温度仍设置为5.45℃。

下面根据围岩的导温系数，计算洞身开挖后14个月后的温度影响情况。

根据计算结果可知，以隧道几何中心为圆心，距离开挖轮廓线22.31m范围内的岩体均会受到洞内温度的影响。

3 数值计算结果分析

在选取模型边界时，经验表明若取计算边界为隧道等效直径的3～5倍，则边界误差在10%以内。依据以上经验，本次的温度场计算模型中，整个断面取136.52×115.94m2，隧道顶至地面为65.022m，隧道轮廊线到模型边界线的两侧距离为40.02m，下面距离为39.998m[1]，如图2所示。本次的温度场采用plane55单元进行计算。本计算模型在计算隧道冻土围岩温度场时取DK141＋624处这一特征断面，距离洞口51m。在分析中，考虑了水文地质条件、大气温度和地温随时间变化的影响。2010年1月布置测温断面，根据所选特征断面的施工情况，做ANSYS模拟，如图3所示。

4 气温持续影响14个月温度场（2011年3月）

软件模拟从2010年1月至2011年3月时间段内在忽略洞内温度影响与在洞内施加气温两种情况下，岩体温度的影响范围（见图4）。根据模拟结果显示，岩体的温度影响范围为21.74m。

图4 气温持续影响14个月温度场（2011年3月）

总结以上实测值与理论计算值的比较，温度的总体趋势都符合实际温度的变化规律，但是考虑到实际量测工程中，可能存在特殊的一段时间温度以及现场量测的误差的存在，同时理论计算是没有考虑岩体裂隙的存在以及地下水的存在，认为围岩是均质各向同性介质等，理论计算温度的施加是根据现场实测的温度拟合施加在裸岩表面，这些都会影响两者的吻合性，但是从总体趋势上分析，计算数据与实测数据还是能反应基本符合关系，由此推断，拟合数据具有一定的科学性，可以指导后续的继续计算及温度的预测。