基于FCD的旅行时间估计算法研究

李亚敏

（交通运输部科学研究院，北京 100029）

0 引言

浮动车技术是目前国际上ITS领域中一种先进的道路交通信息采集技术。利用浮动车进行路段旅行时间数据的采集和预测，能够在数据源上保证数据的精度和可靠性，提高数据的质量。一方面，可以为用户出行提供交通诱导服务，合理地掌握出行时间，提高出行效率；另一方面，可以为交通管理部门提供数据支持，缓解交通压力，提高行车速度。

1 浮动车技术

浮动车是指安装有定位和无线通信装置的普通车辆（如出租汽车、公交车、货车、私人小汽车、警车等），这种车辆能够与交通信息中心进行信息交换。浮动车数据（Floating Car Data，以下简称“FCD”）一般包括时间、位置坐标、瞬时速度、行驶方向、运行状态及其他内容。浮动车技术，是指一定数量的装有特定车载设备的车辆（浮动车），在行驶过程中采集沿途的自身各种交通数据（如：速度、加速度、出行距离、出行时间、停车、超速、紧急情况等），所采集到的实时交通信息通过各种通讯手段传送到信息中心，经信息中心处理后，建立起庞大的共享数据库，并向不同的对象提供多样的实时交通信息。整个过程的实质是对于整个路网的总体车辆进行随机抽样，用样本来反映总体的情况。基于FCD的旅行时间估计包括了浮动车数据采集、地图匹配、数据预处理、预测估计四个步骤。

2 基于FCD的旅行时间估计模型建立

2.1 Kalman滤波模型的建立

浮动车数据可以获得实时的路段旅行时间，在一定范围内，路段旅行时间的序列具有自相关性，因此可以用过去几个时段的路段旅行时间预测下一个时段的路段旅行时间。本模型考虑前n个时段路段的旅行时间对当前时刻旅行时间的影响，用k，k-1，…，k-n+1时段的路段旅行时间预测k+1时段的路段旅行时间。

利用Kalman滤波理论，建立如下递推方程组：

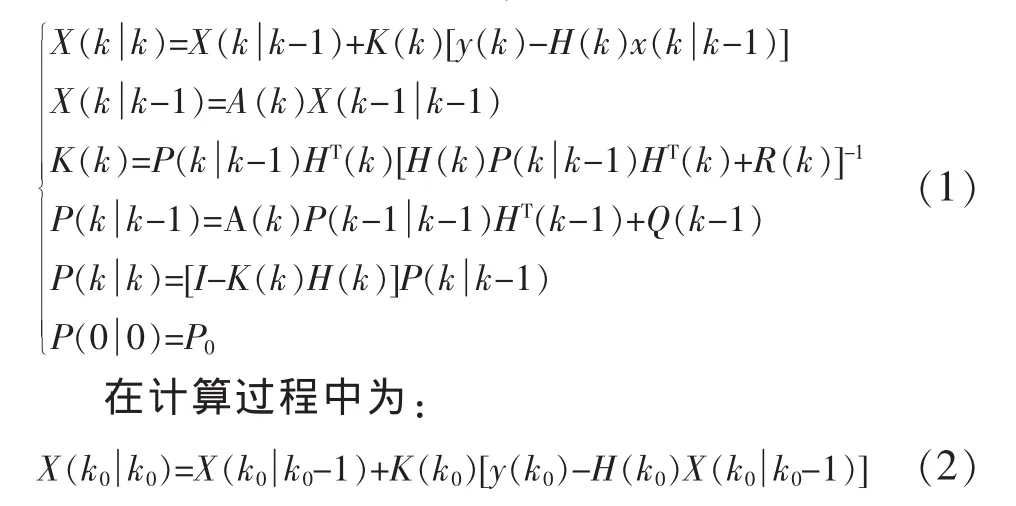
当X（k）确定后，路段在下一个时段的旅行时间的预测值为：

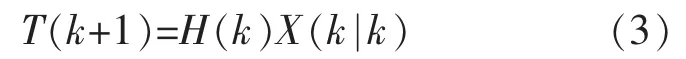
式中，T（k+1）为预测的路段旅行时间；H0（k），H1（k），…，Hn-1（k）为参数矩阵；w（k）为观测矩阵，假定为零均值的高斯白噪声，其协方差矩阵为R（k）；X（k）为状态向量；y（k）为观测向量；H（k）为观测矩阵；A（k）为状态转移矩阵，A（k）=I；w（k-1）为模型噪声，假定为零均值的高斯白噪声，其协方差矩阵为Q（k-1）；v（k）为观测噪声，假定为零均值的高斯白噪声，其协方差矩阵为R（k）。由于本文选取的时间段比较短，前后相邻两个周期的交通状态差别不是很大，所以A（k）取单位矩阵。R（k）、Q（k）、P0没有先验数据，可设为单位矩阵。

算法流程如图1所示。

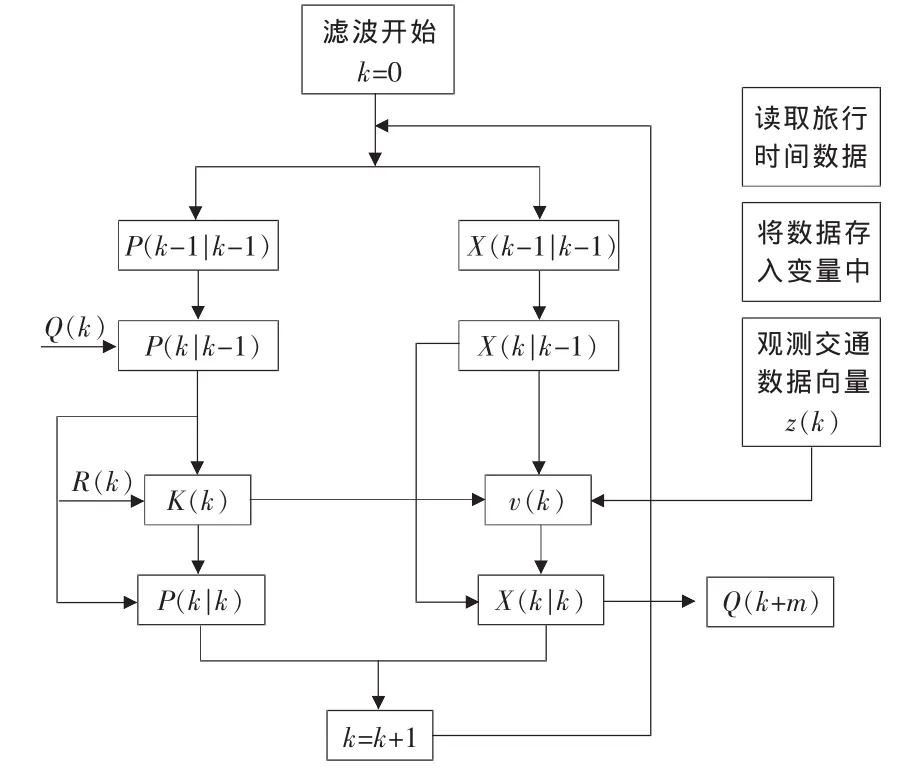
图1 Kalman滤波算法流程

2.2 BP神经网络模型的建立

本文建立的BP神经网络的路段旅行时间预测模型，是基于研究路段及相关路段前几个时段的平均旅行时间与研究路段下一个及以上时段的平均旅行时间的关系建立的。即输入变量为研究路段及相关路段前几个时段的平均旅行时间，输出变量为研究路段下一个或一个以上时段的平均旅行时间，即达到预测目的。

根据得到的2007年6月7日的上海市浮动车所检测到的旅行时间数据，基于BP神经网络，构建旅行时间估计模型如图2所示。

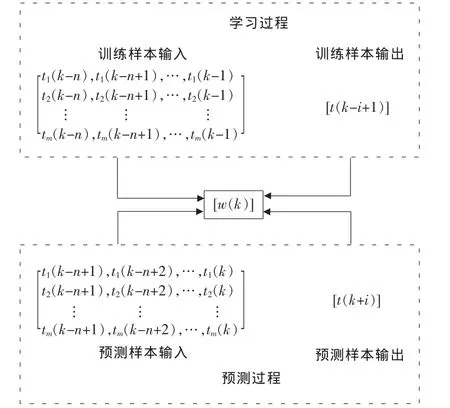
图2 BP神经网络输入输出示意图

模型中各变量意义如下：

t1（k），t2（k），…，tm（k），t（k）——相关路段及研究路段k时段的平均旅行时间；

w（k）——k时段神经网络学习权重矩阵，用来预测k+i时段的平均旅行时间。

3 实例分析

3.1 示例选取

为保证评估具有代表性和可操作性，挑选上海市内的快速路、地面主干道和一条国道进行：

a）快速路选取内环高架从鲁班路立交至漕溪北路匝道的双向道路（单向约4.7km）；

b）地面主干道选取中山南二路从鲁班路至漕溪北路的双向道路（单向约4.7km）（如图3所示）；

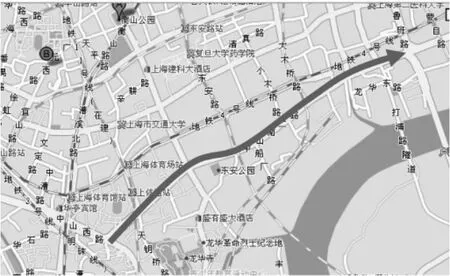
图3 鲁班路立交至漕溪北路匝道高架和地面主干道地图

c）国道选取318国道（沪青平公路）从外环至赵巷镇的双向道路（单向约18km）。

取检测周期为5min，平均速度为40km／h，道路覆盖率达到65%的情况下计算各路段所需最小浮动车数量及误差情况。选取2010年6月6日测量的中山南二路从鲁班路至漕溪北路的西向东单向道路上的双峰路—宛平南路路段进行预测，时段为7:35～10:40（如图4所示）。

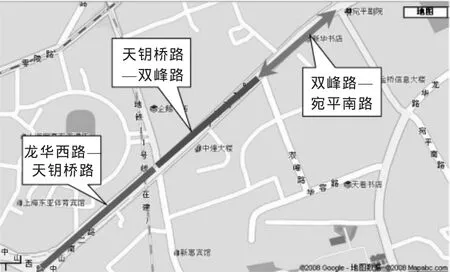
图4 预测路段（双峰路—宛平南路）及上游相关路段

3.2 预测过程及结果分析

3.2.1 Kalman滤波模型预测

本节应用建立的Kalman滤波模型，选取5min为一个时间间隔，预测下一个5min的路段旅行时间时，以k-1时段的路段旅行时间预测k时段的路段旅行时间。

图5所示为预测结果与实际值的对比曲线。

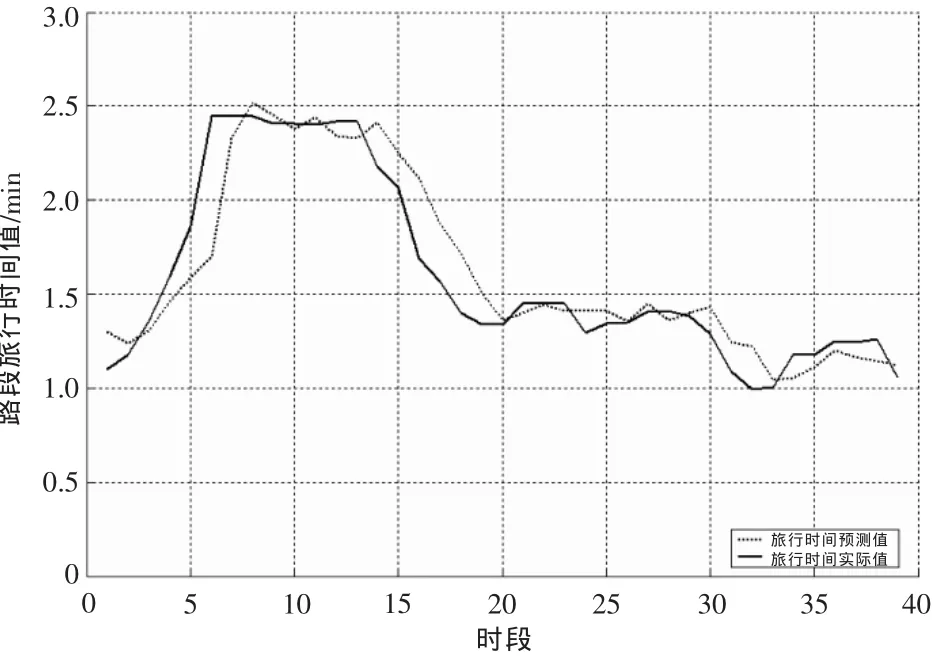
图5 基于FCD的路段旅行时间估计（Kalman滤波）

由图5可以看出：

a）基于浮动车数据，应用Kalman滤波模型进行路段短时预测可以取得较高的预测精度；

b）应用Kalman滤波预测时，由于每次预测都是基于前一时段的旅行时间数据，当数据发生变化时，部分预测值与实际值相比较会出现一定的时滞现象；

c）相比而言，低峰时段的预测值较高峰时段的预测值更为准确和平稳；

d）当旅行时间实际值发生突变时，预测效果较差，由此可见，Kalman滤波模型在预测路段旅行时间时，如果出现由于交通事故或者天气原因造成的突变，可能会有较大的预测误差。

3.2.2 BP神经网络预测

本节应用建立的BP神经网络模型，以5min为一个时间间隔，选取上游的龙华西路—天钥桥路路段、天钥桥路—双峰路路段，以k-2，k-1，k时段的路段旅行时间分别预测k+1时段的路段旅行时间。

图6所示为预测数据与实际值的对比曲线。

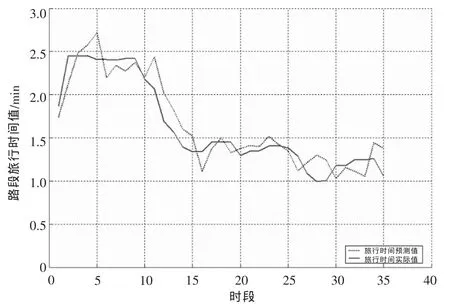
图6 基于FCD的路段旅行时间估计（BP神经网络）

由图6可以看出：

a）基于浮动车数据，应用BP神经网络模型进行路段短时预测可以得到较高的精度，与实际的旅行时间可以较好吻合；

b）应用BP神经网络预测时，在高峰时段预测效果较差，且数据有时会发生一定的突变，而且每次初始化网络时都是随机的，而且训练终止时的误差也不完全相同，结果训练后的权植和阀也不完全相同，所以训练后的结果也不同，数据的准确度也会有差别；

c）当实际值变化不大时，除个别时段外，预测效果普遍较好；当时实际值变化较大时，预测效果变差。

在实际应用中，应用BP神经网络进行旅行时间预测还存在以下问题：

a）收敛速度慢；

b）学习不稳定，容易陷入局部极小点，网络的学习时间和学习效果受初始状态影响，而初始状态的选择在BP神经网络中是随机的，仿真试验可以多次运行寻找满意解，可是实际预测不太可能提供足够的时间来寻求满意解，这就造成了实际预测结果的不稳定；

c）虽然预测趋势大体吻合，但是在某些预测位置点存在预测延迟现象，很难对一些突变点进行预测。

3.3 误差分析

3.3.1 定义误差指标

对预测结果进行误差分析，各误差指标定义如下。

3.3.1.1 平均误差（AE）

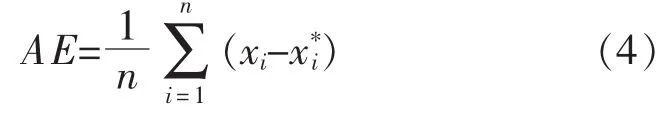
式中，xi为实际值；x*i为预测值。

3.3.1.2 平均绝对误差（MAE）

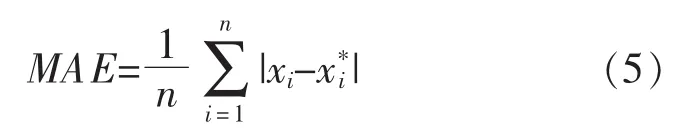
3.3.1.3 平均百分比绝对误差（MAPE）

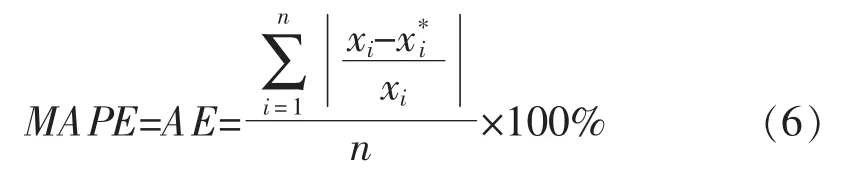
3.3.1.4 均方根误差或标准误差（RMSE）

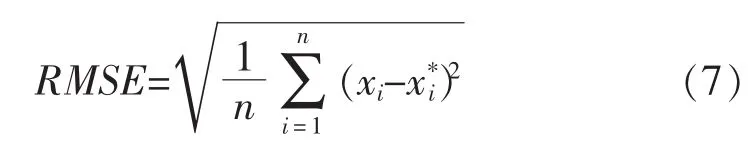
3.3.2 预测结果误差指标值及分析

利用误差指标，对两种模型预测出的结果与真实值作比较，计算误差结果见表1、图7。

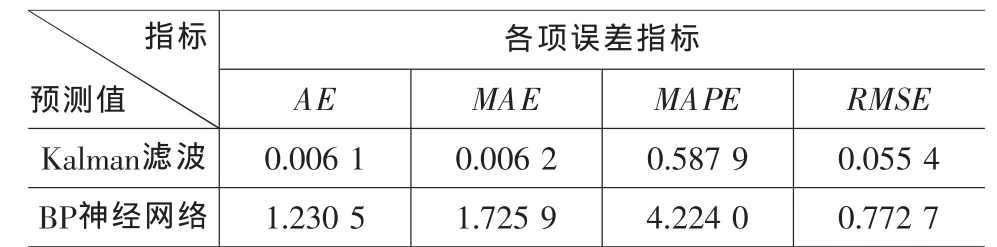
表1 旅行时间估计结果误差指标对比表

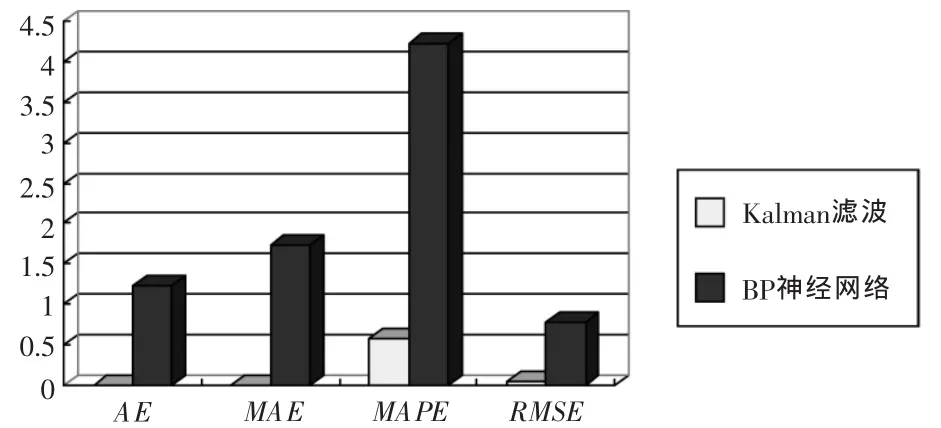
图7 旅行时间估计结果误差指标对比图

由表1可以看出，利用Kalman滤波模型与BP神经网络分别进行旅行时间估计，其各项误差指标均在可接受的范围内，说明基于浮动车数据利用这两种预测方法进行预测是可行的。

比较两种模型的各项指标可得，利用Kalman滤波模型对路段短时旅行时间进行预测比利用BP神经网络模型进行预测的预测精度更高。说明进行短时旅行时间估计时，Kalman滤波方法适用性更好。根据Kalman滤波的工作原理，每一步都要进行增益矩阵和观测矩阵的调整，而这些调整都是以误差为基础的，除了时间分量以外，以往的研究所采用的速度、车流量、车道占有率等数据的波动一般较大，将其引入状态向量中必然会引起大幅震荡，导致矩阵有大的调整，易使预测结果发生大的偏差，导致预测精度差。采用浮动车数据，可以方便地获取路段旅行时间实际值，数据的变化较为平稳，容易得到较好的预测精度。

4 结语

本文根据Kalman滤波模型以及BP神经网络的优点，选取了以上两种模型进行旅行时间估计。通过建立符合浮动车数据特点的相应的模型算法，选取合适的参数进行定量的计算预测。比较最后的预测结果图，相对于BP神经网络模型，Kalman滤波模型的预测值与真实值更加吻合，波动也较小；通过误差指标比较图和比较表可看出，从整体来看，Kalman滤波模型的各项误差指标均小于1且远小于BP神经网络的误差，可以得到比BP神经网络更为接近实际的预测值。由于Kalman滤波本身的动态性、实时性、可操作性强、计算量少的优点，且其模型的递推形式有利于计算机编程的实现，算法的实时性也满足实际预测系统的要求，可应用于基于FCD的路段旅行时间短时预测及相关的交通智能控制系统。

[1]秦岭，张剑飞，郭鹏，等.浮动车交通信息采集与处理关键技术及其应用研究[J].交通运输系统工程与信息，2007，（1）：39-42.

[2]杨兆升.关于智能运输系统的关键理论——综合路段行程时间预测的研究[J].交通运输工程学报，2003，（1）： 65-67.

[3]杭明升，杨晓光，彭国雄.基于卡尔曼滤波的高速道路行程时间动态预测[J].同济大学学报：自然科学版，2002，（9）：1068-1072.

[4]杨兆升，孙喜梅.实时动态路段旅行时间预侧的一种实用方法[J].公路交通科技，2001，（2）：44-65.

[5]Christian E Dunkerley.The effect of disruptions on travel times:a regression analysis from Colombia[DB/OL].http://www.iasi.cnr.it/ewgt/13conference/74_dunkerley.pdf,2008-05-20.

[6]王均，关伟.基于Kalman滤波的城市环路交通流短时预测研究[J].交通与计算机，2006，（5）：16-19

[7]Turner S M,Holdener D J.Probe Vehicle Sample Size for Real-Time Information:The Houston Experience[R].New York:Vehicle Navigation and Information System(VNIS)Conf.IEEE，1995.

[8]董敬欣.基于GPS/GIS的浮动车技术在城市路网分析与评价中的相关方法及应用研究[D].北京：北京交通大学，2005.