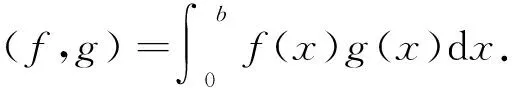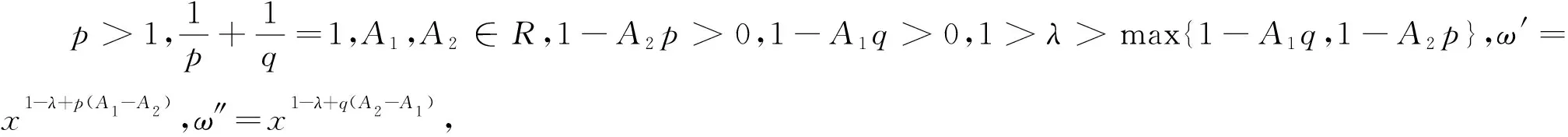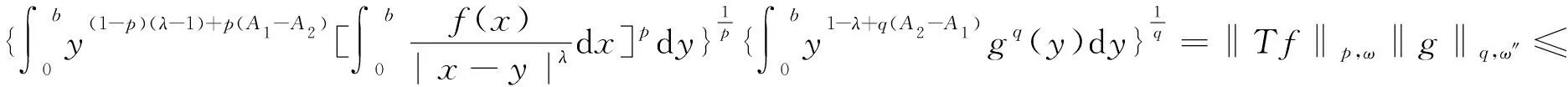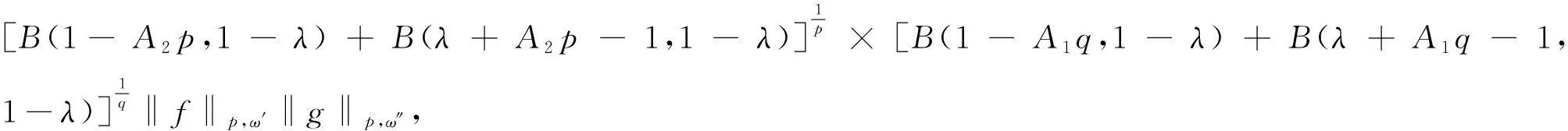一类广义的带参数的Hilbert型奇异积分算子及其应用
2013-11-20陈广生丁宣浩
陈广生, 丁宣浩
(1.广西现代职业技术学院 建筑与信息工程系,广西 河池 547000; 2.重庆工商大学 数学与统计学院, 重庆 400067)

(1)
(2)
这里的常数因子π/sin(π/p)与[sin(π/p)]p是最佳的.式(1)称为Hardy-Hilbert积分不等式,它在分析学中有重要的应用[2].文献[3]首先引人多参数,对式(2)进行了推广.文献[4-5]引入独立参数λ,建立了下列新的Hilbert型积分不等式:
设p>1,1/p+1/q=1,0<λ<1,f(x),g(x)≥0.
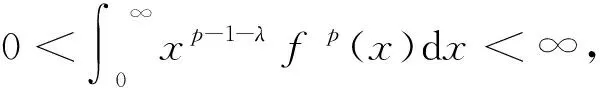
(3)
这里的系数kλ(p)=B(λ/p,1-λ)+B(λ/q,1-λ)是最佳的.
(4)
这里的系数kλ(p)=B(λ/p,1-λ)+B(λ/q,1-λ)是最佳的.
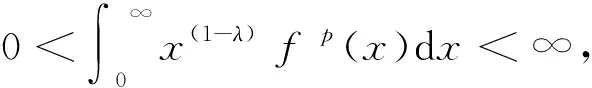
(5)
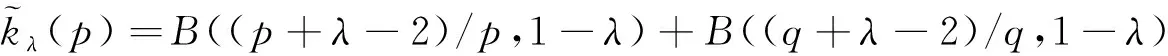
钟五一[6]将式(3)、(4)和(5)进行了如下的统一推广:
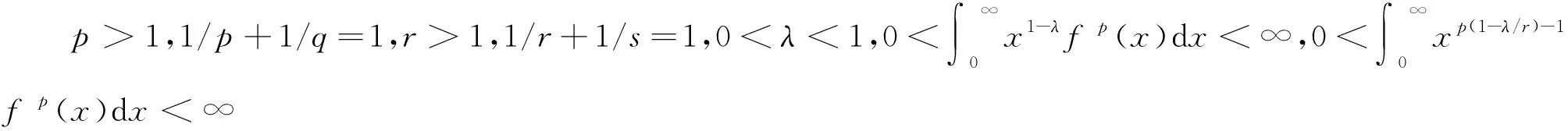
(6)
这里的系数kλ(r)=B(λ/r,1-λ)+B(λ/s,1-λ)是最佳的.
本研究的目的是在区间(0,b)上引入一个Hilbert型奇异积分算子,并讨论其有界性问题.作为应用,导出其等价式及一些相关不等式.
1 主要结果
引入独立参数λ,建立如下的Hilbert型奇异积分算子:
(7)
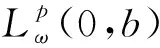
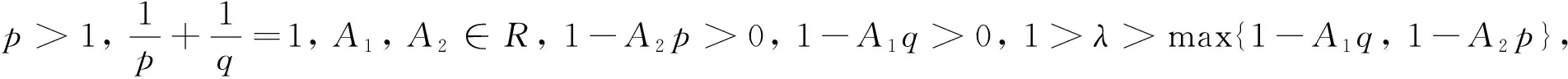
(8)
(9)
则有
ωλ(x,A2,p)≤x1-λ-A2p[B(1-A2p,1-λ)+B(λ+A2p-1,1-λ)],
(10)
ωλ(x,A1,q)≤y1-λ-A1q[B(1-A1q,1-λ)+B(λ+A1q-1,1-λ)].
(11)
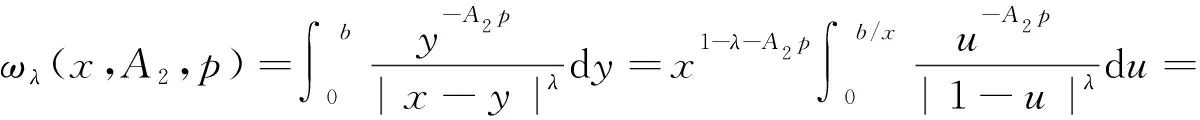
B(λ+A2p-1,1-λ)],因此有ωλ(x,A2,p)≤x1-λ-A2p[B(1-A2p,1-λ)+B(λ+A2p-1,1-λ)].
同理可证明ωλ(x,A1,q)≤y1-λ-A1q[B(1-A1q,1-λ)+B(λ+A1q-1,1-λ)].
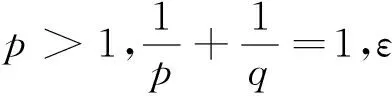
max{1-A1q,1-A2p},则有
(12)
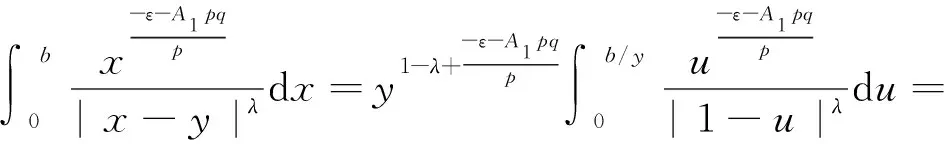
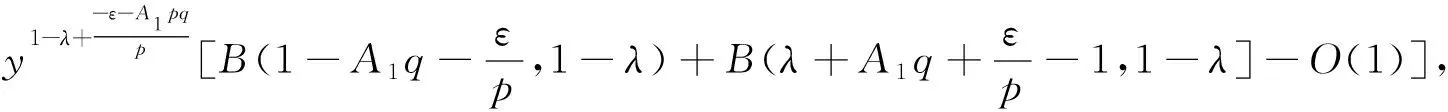
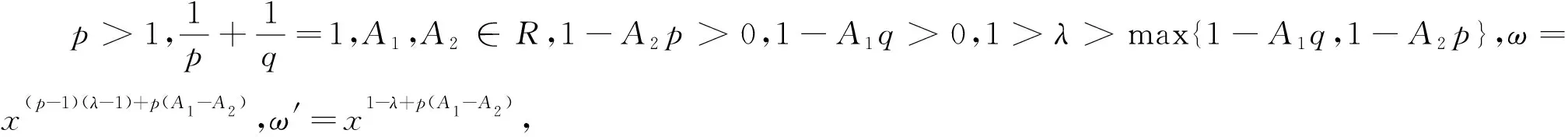
(13)
若还满足A2p+A1q=2-λ,则有
‖T‖=B(1-A2p,1-λ)+B(1-A1q,1-λ).
(14)
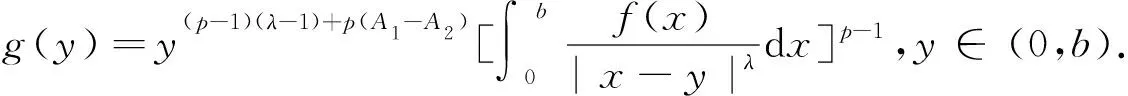
由Hölder不等式[7]得
由引理1得
从而得到
故式(13)成立.
下面证明式(14)成立.
若A2p+A1q=2-λ,则有(1-A2p)(λ-1+A2p)=(1-A1q)(λ-1+A1q)=(1-A1q)(1-A2p),于是有‖Tf‖p,ω≤[B(1-A2p,1-λ]+B(1-A1q,1-λ)]‖f‖p,ω′,故‖T‖≤[B(1-A2p,1-λ)+B(1-A1q,1-λ)]|.若式(14)不成立,则存在常数0 故有 再由引理2得 令ε→0+,则有[B(1-A2p,1-λ)+B(1-A1q,1-λ)]≤K,即有[B(1-A2p,1-λ)+B(1-A1q,1-λ)]≤K,矛盾,所以‖T‖=[B(1-A2p,1-λ)+B(1-A1q,1-λ)]. (15) 证明设ω=x(p-1)(λ-1)+p(a-b),由Hölder不等式及式(13),有 由式(15)可导出式(13),故式(13)与(15)等价. (16) (17) 证明在定理1和推论1中,取A1=A2=A,便可得到(16)式和(17)式. 参考文献: [1] Hardy G H,Littlewood J E,Polya G.Inequalities[M].Cambridge:Cambridge University Press,1952. [2] Mitrinovic D S,Pecaric J E,Fink A M.Inequalities Involving Functions and Their Integrals and Derivatives[M].Boston:Kluwer Academic Publishers,1991. [3] Yang B C.On an extension of Hilbert's integral inequality with some parameters [J].J Math Anal Appl,2004(1):1-8. [4] 杨必成.一个新的Hilbert型积分不等式及其推广[J].吉林大学学报:理科版,2005,43(5):580-584. [5] 杨必成,梁宏伟.一个新的含参数的Hilbert型积分不等式[J].河南大学学报:自然科学版,2005,35(4):4-8. [6] 钟五一,杨必成.一个新的Hilbert型积分不等式的含多参数的最佳推广[J].江西师范大学学报:自然科学版,2007,31(4):410-414. [7] 匡继昌.常用不等式[M].济南:山东科学技术出版社,2004.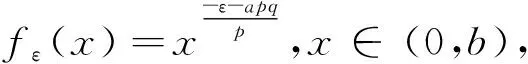
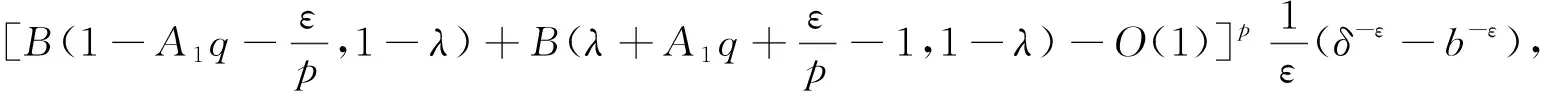
2 一些应用