裤装后上裆倾斜角与上裆长增量的关系研究

何银地，鲁露露

(1.安徽农业大学 轻纺学院, 安徽 合肥230036；2.东华大学 服装学院, 上海 200051)

裤装是服装重要的组成部分，它结构设计的关键在于上裆结构设计，影响裆位舒适合体性的因素很多，诸如臀围放松量、前后裆部宽度、前后上裆倾斜角、下裆倾斜角以及前后裆弧线长等.其中,后上裆倾斜角的大小直接影响着前后裆部弧线与人体臀沟、臀底的配合度，并与后上裆长增量有着一定的量的关系.根据人体体型特征，利用数学手段分析后上裆倾斜角与上裆长增量的关系，为进一步量化裤装版型提供理论依据.

1 裤装结构设计原理

裤装必须包覆人体腹臀部和腿部各复杂曲面，它与人体之间的关系如图1所示.

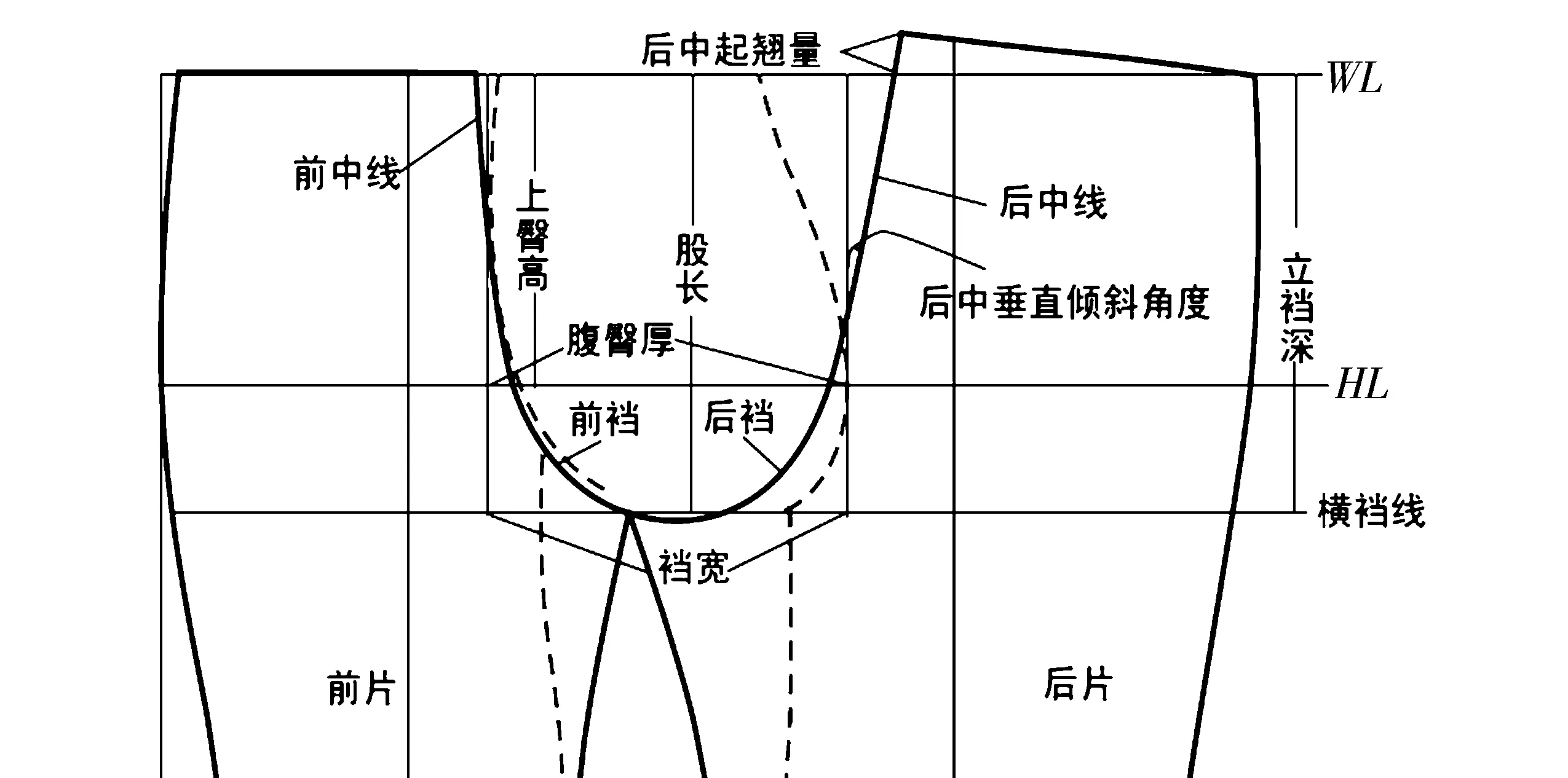
图 1 人体形态和裤装结构的对应关系Fig.1 The corresponding relations of the human hip and pants structure

由图1可以看出,裆宽对应人体腹臀宽，横裆线对应大腿根围的大小，后上裆倾斜角、臀腰差及后上裆起翘量对应人体的臀凸大小，前裆倾斜角对应人体的腹凸大小，立裆深对应人体上裆长，腰、臀围线分别对应人体的腰、臀围，前后片裆部缝接点对应人体会阴点[1].

2 后上裆倾斜角与上裆长增量的关系

裤装的款式风格按裤装臀围的宽松量进行分类，可分为贴体类裤、较贴体类裤、较宽松类裤和宽松类裤.裤装款式风格还体现在裤后上裆倾斜角的差异上，根据裤后上裆倾斜角的大小，裤装也可分为贴体类裤、较贴体类裤、较宽松类裤、宽松类裤和裙类裤.

裤装上裆中后上裆倾斜增量、后上裆倾斜角和上裆长增量三者名词图解见图2，三者之间相互制约，其中后上裆倾斜角与后上裆长增量的设计直接影响裤装上裆长.上裆长过短，使裤子自下裆到臀部出现紧绷状态的皱褶，而且上裆缝会紧贴人体，严重时甚至嵌入臀沟.上裆长过长，裤身下沉，裤子在裆部与人体的空间过大，裤裆下有许多余量形成松散褶皱，容易在走动时对裤腿产生牵扯进而影响人体的跨步运动.

裤装后上裆倾斜角与上裆长增量在量上的定性关系见表1.从表1可以看出，随着上裆倾斜角的增加，裤装结构类型由裙裤类向贴体类裤变化，并且上裆长增量也呈减少的趋势.因而，在上裆长确定的条件下，后上裆倾斜角与上裆长增量之间具有一定的关系[2].

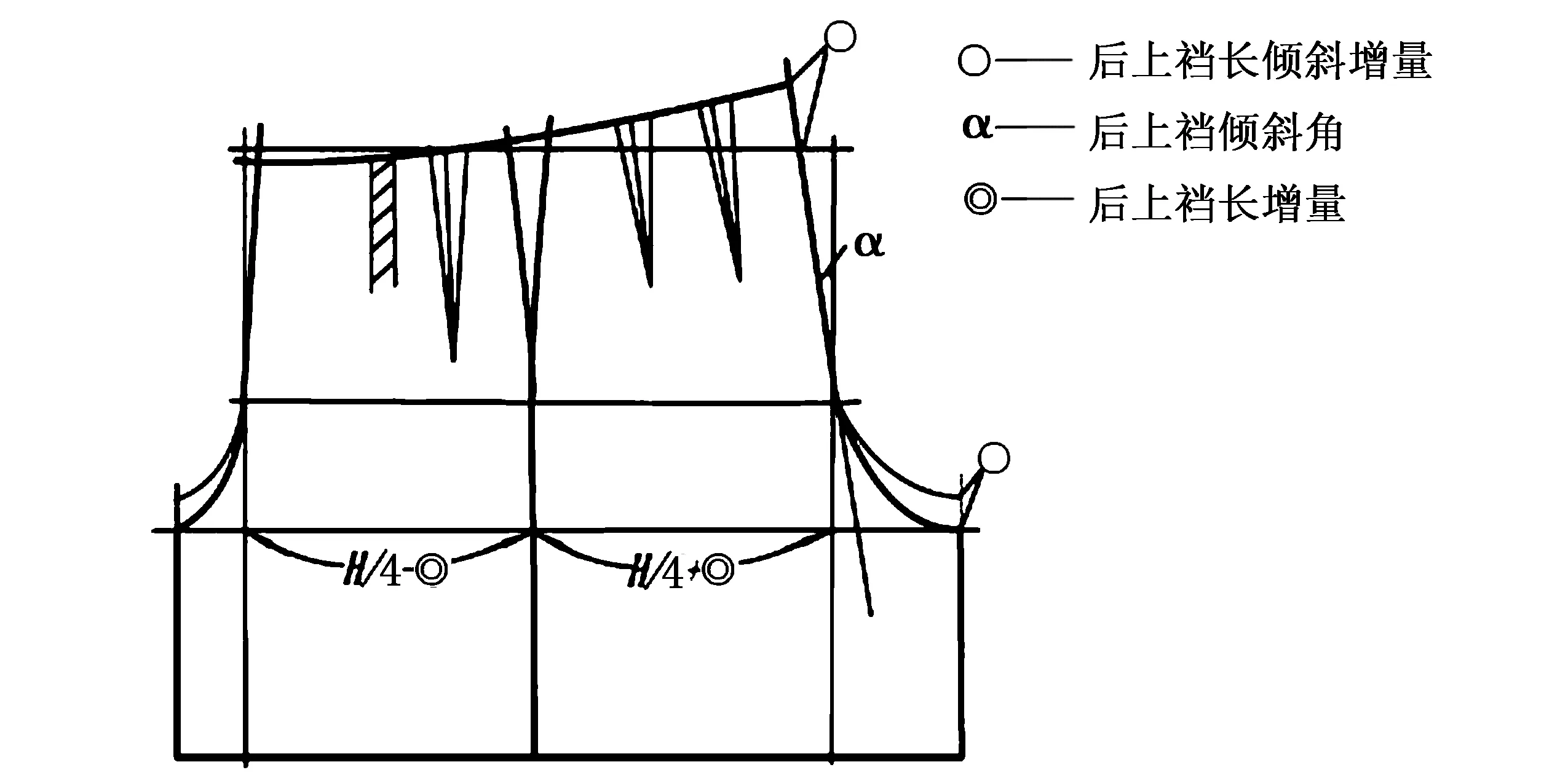
图2 裤装上裆示意图Fig.2 Sketch map of pants crotch

裤类后上裆倾斜角/(°)上裆长增量/cm裙裤类03宽松类0～52～3较宽松5～101～2较贴体10～150～1贴体类15～200

3 后上裆倾斜角与上裆长增量函数关系的建立

3.1 后上裆倾斜角对裤装裆部的影响

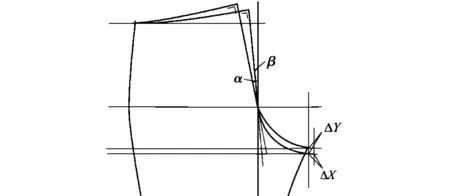
图3 后上裆倾斜角改变的示意图Fig.3 Sketch map of pants back crotch angle

裤装必须包覆人体腰腹和腿部的复杂曲面，裤装纸样设计的关键在于正确把握前后裆宽、后上裆长倾斜增量、后上裆长增量和后上裆倾斜角等参数的选择.为了更加直观地研究后上裆倾斜角对裤装裆部的影响，可通过数学模型寻求后上裆倾斜角对裤装裆部影响的变化规律.当后上裆倾斜角由α(贴体裤装后上裆倾斜角)变化为β时，为保持基本的后裆长度，则上裆有一增长量△Y，此时裤装后裆宽度也会有一定的增量△X[3],如图3所示.

3.2 数学模型解析

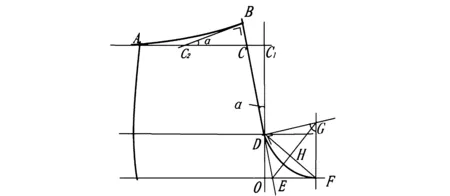
图4 后裆部数模示意图Fig.4 Mathematiccal model of back crotch

传统的裤子后上裆弧线的画法比较精炼且易于掌握,其后裆弧线的起点可近似地认为是后上裆斜线与后裆弯的交点，终点为后裆宽的位置点，将这两点用直线连接，使后裆斜线与横裆线构成一个钝角三角形，然后过此两点做圆弧并与后裆斜线和横档基准线相切，如图4所示.图中D点为后裆斜线与后裆弯的交点；E点为后裆斜线与横裆线的交点，即弧DF的两切线的交点；F点为后裆宽端点；G点是过D点与F点并与裆斜线BD相切的圆的圆心；H点为DF与EG的交点.弧AB部分可将其理想化与直线AC1和BC2相切的一段圆弧[4].

这个数学模型的计算方法如下：

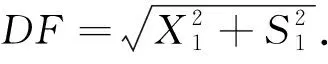
因为点D与点F是以点G为圆心的一段圆弧，并且与直线BD和OF相切，则圆心角∠DGF=2∠DGE=2∠EDF.

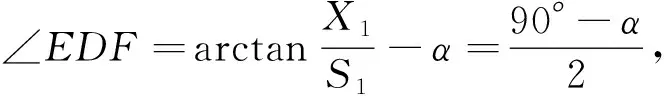
(1)

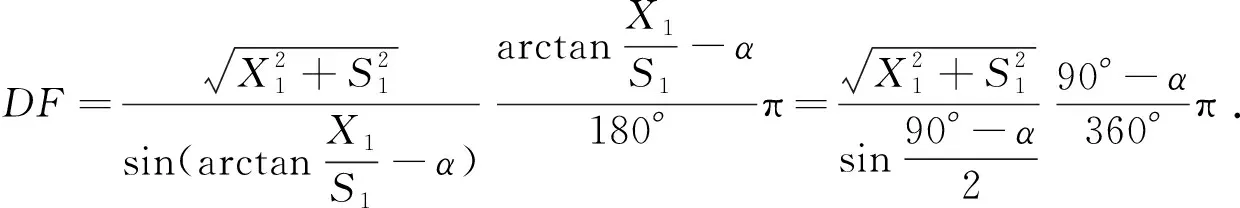
图3中，腰围线AB理想化为与直线AC1和BC2相切的一段圆弧.根据相似三角形原理,得∠BC2C=∠C1DC=α,于是弧AB所在圆心角也为α，故弧AB、后上裆倾斜增量与后上裆倾斜角存在如下关系(令后上裆倾斜增量为μ):

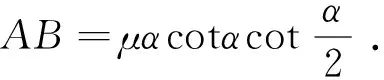
(2)

无论后上裆倾斜角如何变动，图4中弧AB和C1D的取值不会变化(对于同一规格标准)，此时令C1D=v,则此时的上裆长可表示为

(3)

同理，当上裆倾斜角为β时，如图4所示，此时上裆长有一增量△Y，且裆部宽度也有一增量△X,则后上裆长可表示为

(4)

L1=L2.

(5)

于是，S1=F(X1，α),S2=F(X2，β)又△Y=S2-S1,此时后裆宽变化量△X=X2-X1.

综上，联立式(1)，(2)，(3)，(4)，(5)，可得出△Y=F(X2，β)-F(X1，α)[5].

3.3 验证

3.3.1 实验对象确定

为进一步验证上式，以较贴体女裤后片上裆部分(后上裆倾斜角取13°)为研究对象.规格设计为W*=68,则W=W*+2=70，H*=90，则H=H*+10=100，BR=0.25H+2=27 cm,总上裆宽=0.15H=15 cm,后上裆宽=0.11H=11 cm.

3.3.2 计算

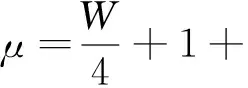
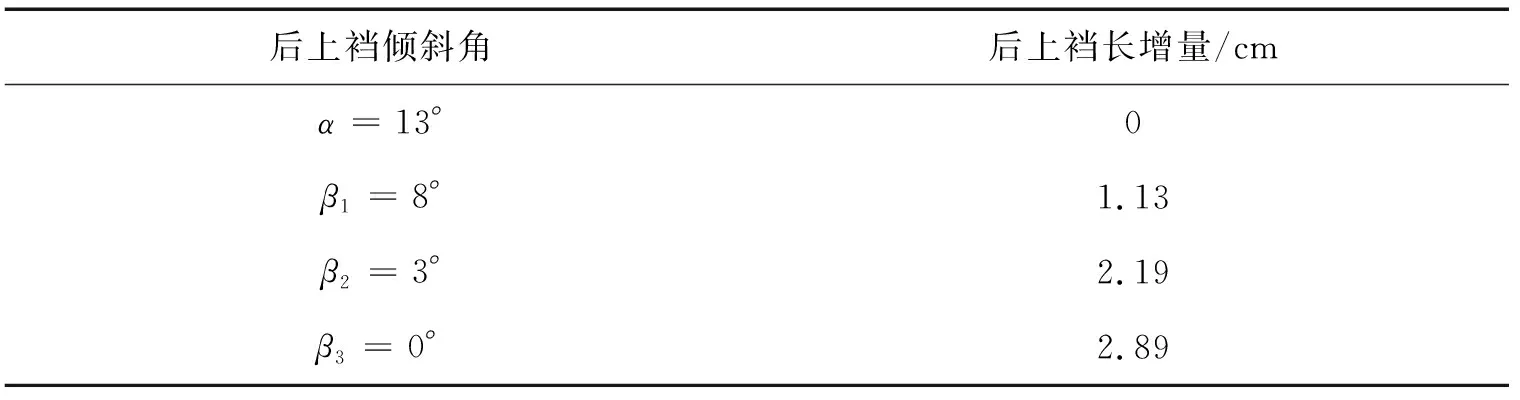
表2 后上裆长增量的理论值Tab.2 The retical value of back crotch length increment

3.3.3 实际测量

利用1∶1制图，画出后上裆倾斜角分别为13°，8°，3°和0°时后裤片上裆纸样，测量出上裆长变化量△Y1′，△Y2′以及△Y3′.

当α=13°，β1=8°时，得出△Y1′=0.94 cm；

当α=13°，β2=3°时，得出△Y2′=1.93 cm；

当α=13°，β3=0°时，得出△Y3′=2.50 cm.

3.3.4 实际尺寸与理论值对比分析(见表3)

表3 实际尺寸与理论值的对比Tab.3 Comparison between actual size and theoretical value

由表3可知，后上裆长增量的变化基本与理论相符，随着上裆倾斜角的变小，为保证裤装上裆弧线与人体的臀沟形态的最佳匹配状态，后上裆倾斜增量会随之减少，并且上裆长会有一定的增量，这种关系可体现在裤装结构为贴体型向裙裤结构变化的过程中.

4 结论

通过以上的数学分析与验证，可以得到后上裆倾斜角和上裆长增量的变化关系，随着后上裆倾斜角的变小，上裆长增大，而后上裆倾斜增量随之减少，且上裆长增量满足函数关系式△Y=F(X2,β)-F(X1,α).

从结果看，实际测量结果与理论值具有一定的误差，这主要是所建立的模型将腰线与裆弯部位理想化为圆弧，但这两个部位的曲线曲率均较实际裤装结构曲线大，这也是出现理论值大于实际值的一个原因.此外,影响裤装上裆结构的因素很多，本研究排除了其他诸多与裆部结构有关的因素，诸如裆宽、下裆倾斜角、材料拉伸性能以及松量等，因而得出的结果具有局限性，在实际应用中也会出现偏差，今后还可以结合面料特性作更进一步的研究.

参考文献:

[1] 吴俊.女装结构设计与应用[M].北京：中国纺织出版社，2000：1-99.

[2] 张文斌.服装结构设计[M].北京：中国纺织出版社，2006:1-94.

[3] 周惠，王红歌，胡淑蓉.解析裤装下裆倾斜角对裆宽的影响[J].辽东学院学报：自然科学版，2006，13(1):13.

[4] 张金鲜.基于体型特征的裤装结构适应性理论研究[D].上海:东华大学，2005：5-22.

[5] 余国兴,陈冰.女子下体与裤装结构设计[J].东华大学学报:自然科学版，2007,33(6):769-773.