利用GOCE模型分析EGM2008在中国及其邻区的空间相对可信度分布

张丽霞

(广州市地震监测中心，广东 广州 510000）

0 引言

EGM2008是由美国NGA(National Geo-spatial-intelligence Agency)重力场研发小组发布的高阶地球重力场模型，该模型采用GRACE卫星跟踪数据、卫星测高数据和地面重力数据与高分辨率的全球地形数据等，其球谐展开阶数达2 159阶，扩展阶数至2 190阶，空间分辨率达到约9 km[1]。由于受自然地理条件与气候甚至行政、国家安全等因素限制，在地球上很多区域，缺少或难以获得地面实测重力数据，而相对以往重力场模型，精度和分辨率均有很大提高的EGM2008模型可为重力空白或数据稀少区域的工程测量、大地测量、弹道分析、导航、地球物理勘探、区域与深部构造研究等提供一种方便而有效的数据选择[2～7]。

EGM2008所使用的地面重力数据主要是指NGA的5′×5′的全球重力数据库，虽然这个数据库数据的全球覆盖率达到83.8%，但有些地区的重力数据属于专利数据或无数据区，如中国西部与北部区域。为了对全球重力场模型EGM2008的精度进行评估，国外许多研究人员对这些重力场模型进行外部检核[8～10]。在国内，很多学者利用实测GPS水准数据、垂线偏差数据、地面空间重力网格数据与EGM2008解算数据进行对比，分析了模型的精度与可靠性[11～17]。然而，地面实测点位数据数量有限且分布不均匀，加之各期实测数据观测仪器与观测精度不等、处理方法与高程系统不统一，而且由于缺少地面数据无法衡量该模型在中国邻区的精度。基于此，本文利用最新的GOCE卫星重力场模型，采用新方法评价EGM2008模型在中国及其邻区的空间相对可信度分布，通过与其它检验方法对比验证了本文方法的有效性，进而可以为以后其它高阶混合重力场模型的相对可信度评估提供简单而有效的方法，以期为EGM2008模型等的数据使用者在决策与工作设计、精度评价等方面提供依据与参考。

1 EGM2008相对可信度评价方法

对于数据专利区或者无数据区，Pavlis等[1]在构建重力模型时，采用了一种不依赖于任何均衡假说的数据合成的方法来填补这些专利数据区或者无数据区，即利用GRACE卫星数据建立的GGM02S地球重力模型的前60阶球谐系数，加上EGM96重力模型的第61～360阶球谐系数，再加上全球剩余地形模型（即30′′×30′′的DTM2006.0全球地形数据与360阶次高程球谐系数确定的全球高程模型之差）产生的重力效应（2′×2′网格，展成2 700阶球谐模型）的第361～2 160阶球谐系数计算得到重力异常，解算成5′×5′的网格数据后与其它地面数据合成5′×5′的全球重力异常数据库，最后进行调和分析，构建出2 160阶次的EGM2008地球重力模型。由该建模过程可以看出，高阶部分主要反映地形的重力效应，在具有地面数据的区域，仍然包含地下密度异常引起的短波长成分重力异常，但是由于波长较短，进行球谐建模对于数据限制区或者无数据区没有提供地下密度变化的有用信息。根据球谐分析理论，其本质属于球面上的傅里叶变换，空间上任一测点的精度对重力场模型全阶次均有影响，因而重力场模型中低阶部分的数据精度，由于地面数据信息加入而有所提升，但主要集中于120阶以上[18]。加之，纯粹利用卫星测量数据建立的重力场模型在中、低阶部分精度较高，且可以认为其误差在空间上的分布是均一的，因此，其与EGM2008模型解算数据的差值可以用来衡量EGM2008模型相对可信度在空间上的分布[18～20]。

由于最新的GOCE重力场模型展开阶数至250阶，因此首先需要将EGM2008模型解算的网格重力数据进行平均，将其尺度压降到与GOCE重力场模型尺度一致，即：

其中，N为滑动窗口内EGM2008模型解算的网格节点个数，为节点位置的纬度。假设地面实测重力数据的误差满足高斯分布，令其标准差为，则由误差传播定律，压降尺度后的网格节点标准差为：

其中，α为校正因子，即用于平衡地面数据的采样不均匀性。

GOCE卫星重力场模型解算数据与EGM2008模型解算数据的平均重力异常之间的差异均方值δdiff，由于GOCE重力场模型的均方误差为，则

联合式（2）与式（3）可得：

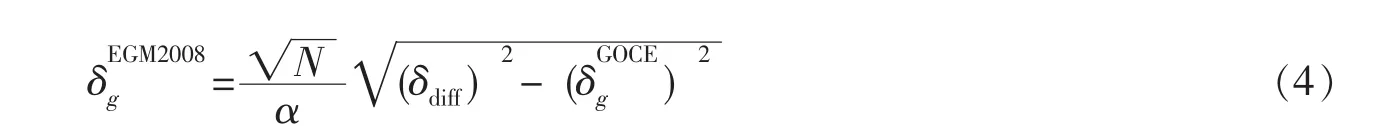
由于不同地区α因子很难确定，而且纯粹利用卫星测量数据建立的重力场模型精度在空间上的分布比较均一，因此由式（4）可知，δdiff分布可以作为EGM2008可信度空间分布的一种相对度量。考虑本文只是着重于模型在空间上的一种相对的可靠性评估，并不是对原始地面数据的绝对误差估计，因此采用了直接截断重力场模型阶次范围的方法计算差值分布。

2 EGM2008可信度空间分布

图1 自由空间重力扰动：Fig 1 Free-space gravity disturbance

首先，分别解算EGM2008模型（2～2 190阶）在长半轴为6.388 136 460×106m、短半轴为6.366 752 314 2×106 m、网格大小为7.5′×7.5′、展开阶次范围为2～2 190阶与网格大小为30′×30′、展开阶次范围为2～250阶的椭球面上的自由空间重力扰动值，结果如图1(a)与1(b)所示。然后，解算GOCE卫星重力场模型（2～250阶）在相同椭球面上的自由空间重力扰动值（网格大小为30′×30′），结果如图1(c)所示，而EGM2008模型与GOCE模型的差值分布如图1(d)所示，可以看出，两者的差值范围为-70～50 mGal，明显在中国大陆中部、东部与南部差值较小，而在西部与北部差值较大。由于GOCE卫星重力场在区域内的误差是均一的，则这种差异的空间分布主要描述了EGM2008模型原始地面数据的相对可信度，此差值分布与地形的复杂程度具有很大的相关性，其原因可能是此地区原始地面数据稀少、观测精度不一致，最大原因可能来源于高程测量的误差。

进而，采用2°×2°的滑动窗口，统计计算窗口内GOCE模型与EGM2008模型2～250阶系数解算的自由空间重力扰动差值的均方根值，其分布如图2所示，其分布与杨金玉等[17]利用地面实测重力网格数据给出的EGM2008模型的精度分布较一致，这说明本文方法是有效的，且图2还展现了该模型在中国临区与海洋区域的相对可靠性分布。选择差值分布较大的区域I与均方根较小的区域II，进行统计分析，结果如图3(a)与3(b)，可见在区域II，EGM2008可信度相对较大。同样，统计全区范围内的差值与差值均方根柱状统计图，如图3(c)与3(f)所示，可见差值均方根的平均值为5 mGal，若假定差值均方根大于15 mGal的区域视为可信度较低的区域，预示着在这些区域，例如，青藏高原东构造结与西构造结、喜马拉雅山地区、新疆西北部与南部、贝加尔活动构造带、海南岛南部、南北地震带、中国东北地区东部、菲律宾海板块西南部与西太平洋俯冲带等等，EGM2008模型所采用的地面重力数据稀少或者精度较低，应该谨慎使用。

图2 EGM2008模型与GOCE模型2～250阶系数解算分布的自由空间重力扰动差值的均方根分布Fig.2 Root mean square of the residual free-space gravity disturbance calculated by subtracting the GOCE field from EGM2008 field up to degree and order 250

3 结论

本文采用新的评价方法，结合最新GOCE卫星重力场模型给出EGM2008模型在中国及其邻区空间相对可信度分布，经分析得出如下结论：

图3 GOCE模型与EGM2008模型2-250阶系数解算的自由空间重力扰动差值的统计图与差值均方根分布Fig.3 Histograms of the residual field and root mean square of the residual free-air gravity disturbance calculated by subtracting the GOCE field from EGM2008 field up to degree and order 250

（1）中国大陆的西部与北部由于属于NGA的重力数据专利区与无数据区，且地形起伏复杂，高程测量误差较大，因而造成EGM2008模型在该区域相对东部区域可信度较低；此外，在贝加尔湖地区、海南岛、南北地震带、中国东北地区东部、菲律宾海板块西南部与西太平洋俯冲带等地区的可靠性也相对较低。

（2）EGM2008属于合成重力场模型，在重力数据专利区或者无数据区，短波长主要由于地形起伏引起，对于大地测量、国防建设等有益，而不适合于小尺度的地球物理勘探，对于区域较大尺度的地质填图或者深部结构研究，建议直接采用最新的卫星重力场模型。

（3）通过与外部检验方法的结果比较，验证了本文方法的有效性，可为今后其它高阶混合重力场模型的空间相对可信度分布的估计提供参考。

[1]Pavlis N K,Holmes S A,Kenyon S C,et al.An Earth Gravitational Model to Degree 2160:EGM2008[C].Vienna：EGU General Assembly,2008.

[2]张兴福,刘成,王兵海,等.无水准数据的GPS高程转化方法及精度分析[J].大地测量与地球动力学，2010， 30(1)： 114-118.

[3]翟振和，魏子卿，吴富梅，等.利用EGM2008位模型计算中国高程基准与大地水准面间的垂涎偏差[J].大地测量与地球动力学， 2011，31(4)：116-118.

[4]刘晓刚，吴晓平，赵东明，等.EGM96和EGM2008地球重力场模型计算弹道扰动引力的比较[J].大地测量与地球动力学，2009，29(5)：62-67.

[5]钱东，刘繁明，李艳，等.导航用重力梯度基准图构建方法的比较研究[J].测绘学报，2011，40(6)：736-744.

[6]林淼，朱建军,田玉淼，等.大地水准面异常在湖南地区的地球物理解释[J].地球物理学报，2012，55(2)：472-483.

[7]陈家联,张毅,陈超.广西地区卫星重力异常与区域地质特征[J].地球物理学进展，2010，25(4)：1233-1239.

[8]Kotsakis C,Katsambalos K,Ampatzidis D,et al.Evaluation of EGM08 in Greece Using GPS and Leveling Heights[C].china：IAG International Symposium on Gravity,Geoid and Earth Observation,2008.

[9]Dawod G,Mohamed H,Ismail S.Evalustion and Adaptation of the EGM2008 Geopotential Model Along the Northern Nile Valley,Egypt:Case Study[J].Journal of Surveying Engineering,2010,136:36-40.

[10]Yilmaz I,Yilmaz M,Gullu M,et al.Evaluation of Recent Global Geopotential Models Based on GPS/Levelling Data over Afyonkarahisar(Turkey)[J].Scientific Research and Essays,2010,5:484-493.

[11]张兴福,刘成,刘红新.利用GPS/水准数据检核EGM2008重力场模型的精度[J].测绘通报，2009， (2)：7-9.

[12]章川银，郭春喜，陈俊勇，等.EGM2008地球重力场模型在中国大陆适用性分析[J].测绘学报，2009， 38(4)： 283-289.

[13]荣敏，周巍，陈春旺.重力场模型EGM2008和EGM96在中国地区的比较与评价[J].大地测量与地球动力学，2009， (6)：123-126.

[14]刘晓刚，吴晓平，田颜峰，等.DQM2000d、UGM05和EGM2008地球重力场模型精度比较[J].测绘通报，2010， (2)：8-10.

[15]束蝉方，李斐，郝卫峰.EGM2008模型在中国某地区的检核及适用性分析[J].武汉大学学报·信息科学版， 2011， 36(8)： 919-922.

[16]张精明，闫建强，王福民.EGM2008地球重力场模型精度分析与评价[J].石油地球物理勘探，45(增刊1)：230-233.

[17]杨金玉，张训华，张菲菲，等.EGM2008地球重力场模型数据在中国大陆地区的精度分析[J].地球物理学进展，2012，27(4)：1298-1306.

[18]Pail R,Bruinsma S,Migliaccio F,et al.First GOCE gravity field models derived by three different approaches[J].Journal of Geodesy， 2011， 85(11):819-843.

[19]Braitenberg C,Mariani P,Pivetta T.GOCE observations in exploration geophysics[C].Proceedings of the 4th International GOCE User Workshop，2011.

[20]lvarez O,Gimenez M,Braitenberg C,et al.GOCE satellite derived gravity and gravity gradient corrected for topographic effect in the South Central Andes region[J].Geophysical Journal International， 2012， 190：941-959.

[21]Wessel P,Smith W H F.Free software helps map and display data[J].Eos Trans.， 1991， 72(41)： 441.