加筋板在热声载荷作用下的非线性动态响应分析

钟皓杰，沙云东，魏 静

(沈阳航空航天大学 航空航天工程学部(院),沈阳 110136)

现代航空航天工程中，为了减轻飞行器重量，大量采用薄壁板壳结构，如导弹的翼面、弹头，发动机燃烧室火焰筒，隔热防护板，飞行器蒙皮等[1-2]。加筋板结构是飞行器结构的典型部件，常用于飞行器机身、机翼和尾翼等此类主承力构件中[3]，可以显著提高结构的承载能力。这些结构在工作时承受着热载荷、机械力载荷、声载荷、压力载荷联合作用，产生复杂的振动应力。

国外研究表明，高超音速飞行器构件结构表面壁板承受的噪声载荷最高可达180dB，温度最高可达3 000 ℉[4-5]。构件长期暴露在这种复杂环境下会引起结构的疲劳失效，严重威胁飞行器可靠性。另外，对于此类受压板件，在热声载荷作用下的稳定性也是结构设计时的主要因素之一[6]。C.Mei等[7]曾采用FEM研究了热声载荷作用下梁的动态响应，C.F.Ng[8-9]曾基于Von Karman方程，利用Galerkin法推导出单模态方程，结合试验研究了薄壁板和曲板在热声载荷作用下的非线性响应以及板结构热声响应的基本特性。

目前国内针对热声激励下结构动态响应的研究较少，沈阳航空航天大学工程振动与噪声研究所沙云东教授等[10-13]采用Galerkin法研究了热声载荷作用下金属、复合材料薄壁板的动态响应问题。本文在此基础上，基于加筋板在热声载荷作用下的大挠度控制方程，通过使用有限元方法仿真模拟，计算了未加筋板与加筋板在热声载荷作用下的非线性动态响应，讨论并比较了两种结构的响应特性。

1 理论分析

1.1 加筋板的大挠度运动控制方程

对于加筋板结构，主体结构与加强筋交织在一起，板和筋之间的力学行为相互间产生耦合，不容易准确的得到它的解析解，因此将加筋板结构简化为便于处理的计算模型，首先将加筋板离散为板和梁的组合结构，对筋与板之间的连接采用“线接触”假设，即忽略筋与板之间的剪切应力，加筋部分截面上的应力分布只与横向位移有关[14]。将每条筋的力与弯矩分别叠加到微段上，运用Hamilton变分原理，可以得到加筋板的非线性控制方程：

(1)

其中δxj、δyi为：

其中f为载荷项和体力项，包括表面随机压力、惯性力、粘性阻尼力：

式中:yi、xj分别为x方向第i根筋和y方向第j根筋中线的位置，a、b为板的长和宽，ti、tj为加筋的厚度，Nx、Ny、Nxy为膜力，Mx、My、Mxy为板内弯矩，ξ为阻尼系数。由于忽略了筋与板之间的剪切力，可引入如下形式的应力函数F：

式中h为薄板厚度。由应变与应力的关系，以及筋与板的变形协调，筋截面上的轴向力Nxi、Nyj可以表示为：

(2)

弯矩Mxi、Myj可用筋的膜力与挠度表示为：

(3)

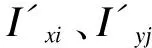
把公式(2)、(3)代入公式(1)，加入考虑了热应变的应力应变关系，并根据薄板大挠度理论得到板的弯矩，整理后可得到加筋板在热声载荷作用下的Von Karman大挠度方程：

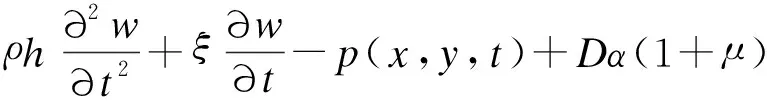
(4)

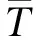
板的中面应变协调方程为：

(5)

由板壳理论可知，四边简支板的挠度可用余弦函数族表示：

(6)

式中:Amn为第(m,n)阶模态幅值，a、b分别为板的长与宽。

当板壳结构处于温度场时，由温度产生的压应力引起的屈曲称为热屈曲，对应于结构热屈曲的温度称为临界屈曲温度[15]。本文仅研究均匀温度场引起的分支型热屈曲，此类热屈曲是一个准静态过程，可不考虑运动方程中的外载荷项和时间相关项；板在初始平衡位置的面内位移为零，则面内应变也为零；考虑热应力合成的内力，将应变协调方程(5)与位移函数(6)代入公式(4)，经各向同性简化与推导可得出四边简支板临界屈曲温度为[16]：

(7)

当m=1,n=1时，可得出四边简支板的一阶临界屈曲温度：

(8)

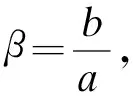
2 数值模拟

本文以四边简支铝合金薄壁板与四边简支铝合金加筋板为计算对象，使用FEM模拟了两种结构在热声载荷作用下的大挠度非线性响应，并对结果数据进行对比分析。施加的声载荷为170 dB，0～1 500 Hz的有限带宽高斯白噪声；施加的热载荷为均匀的温度场S=0～S=2.1。由于计算的温度不是很高，假定材料特性不随着温度载荷的改变而改变。

2.1 模型建立

薄壁板与加筋板的几何模型与有限元模型，如图1所示。

图1 薄壁板与加筋板模型

薄壁板与加筋板几何及材料参数如下表1所示：

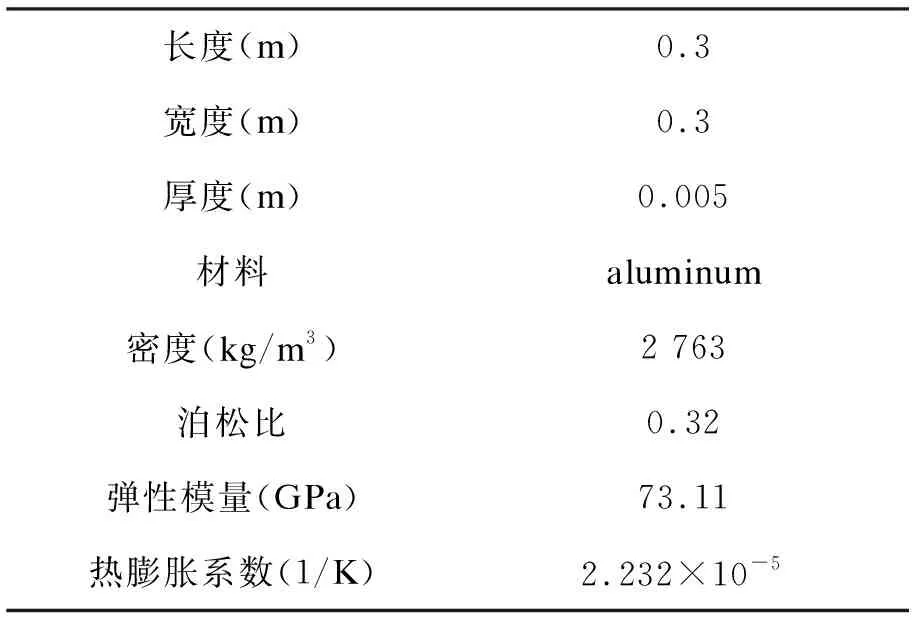
表1 薄壁板与加筋板的几何及材料参数

薄壁板和加筋板的固有模态频率和临界屈曲温度，如表2、表3所示：

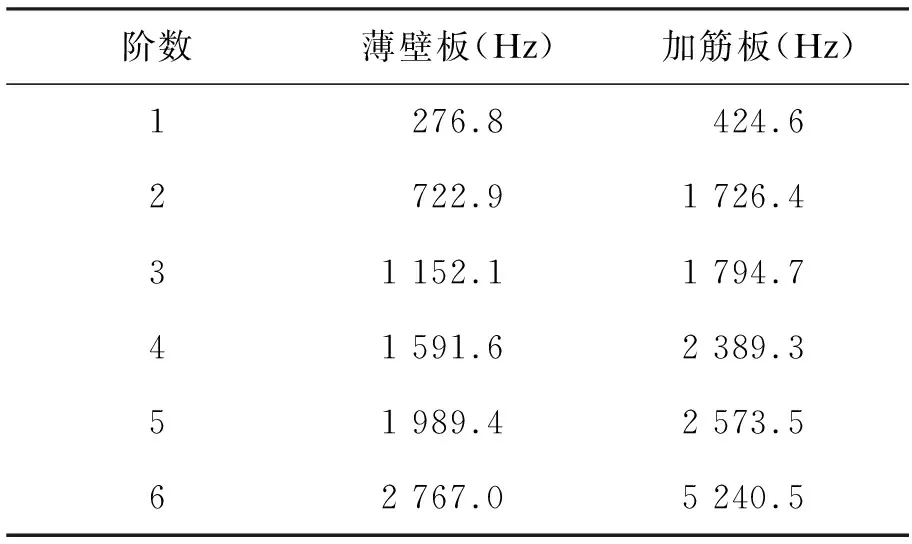
表2 薄壁板和加筋板前6阶模态频率

表3 薄壁板和加筋板前6阶临界屈曲温度

载荷条件取第一阶临界屈曲温度薄壁板为Tc1=15.5 ℃，加筋板为Tc2=56.6 ℃。本文主要讨论的载荷环境为空间均匀分布的高斯白噪声SPL170dB、频率范围0～1 500 Hz，屈曲系数分别取S=0，S=0.7，S=1，S=1.4，S=2.1，分析了该载荷环境下加筋板典型节点位置，即如图1中心点a和点b位置的非线性动态响应。

2.2 数值分析

本文采用FEM，得到了声压级SPL=170 dB下屈曲系数S分别取S=0，S=0.7，S=1，S=1.4，S=2.1的薄壁板与加筋板横向位移时间历程，其中横坐标为时间，纵坐标为无量纲位移，无量纲位移=实际位移/厚度。热声激励下加筋板的典型运动：(1)屈曲前，围绕初始平衡位置的随机振动；(2)屈曲后，围绕两个屈曲后平衡位置的跳变运动；(3)屈曲后，围绕一个屈曲后平衡位置的随机振动，如图2～图6所示。

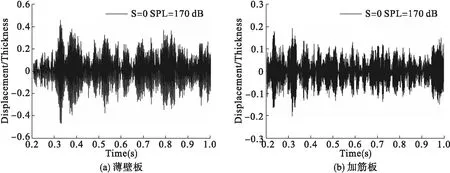
图2 板中心点位置处横向位移时间历程图(S=0，SPL=170 dB)

由图可知，标准温度时，即S=0时，两种结构围绕初始位置进行随机振动，振动幅值较小，其中，薄壁板最大横向位移约为±0.5，加筋板最大横向位移约为±0.2。

随着温度载荷的增加，当S=0.7时，比标准温度载荷时相比，两种结构振动幅值均增大，薄壁板最大横向位移约为±0.7，加筋板最大横向位移约为±1，且薄壁板的时间历程曲线与加筋板相比显得更为稀疏，说明此时在同一热声条件下，薄壁板的振动频率降低的速度明显大于加筋板。

当S=1时，薄壁板最大横向位移约为±0.8，加筋板最大横向位移约为±1.4，此时为临界屈曲状态，加筋板的时间历程曲线也变得较屈曲前稀疏，但薄壁板的变化程度还是更为明显。

图3 板中心点位置处横向位移时间历程图(S=0.7,SPL=170 dB)

图4 板中心点位置处横向位移时间历程图(S=1,SPL=170 dB)

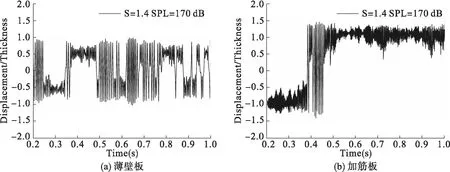
图5 板中心点位置处横向位移时间历程图(S=1.4,SPL=170 dB)

当S=1.4时，两种结构的运动形式发生了很大的改变，都围绕屈曲后两个平衡位置进行跳变运动，振幅也明显增大。但屈曲系数S相同时，薄壁板的跳变频率非常频繁，可见加筋板的稳定性更好。

当S=2.1时，两种结构均围绕屈曲后一个平衡位置进行随机振动。

位移响应均方根值如表4所示。

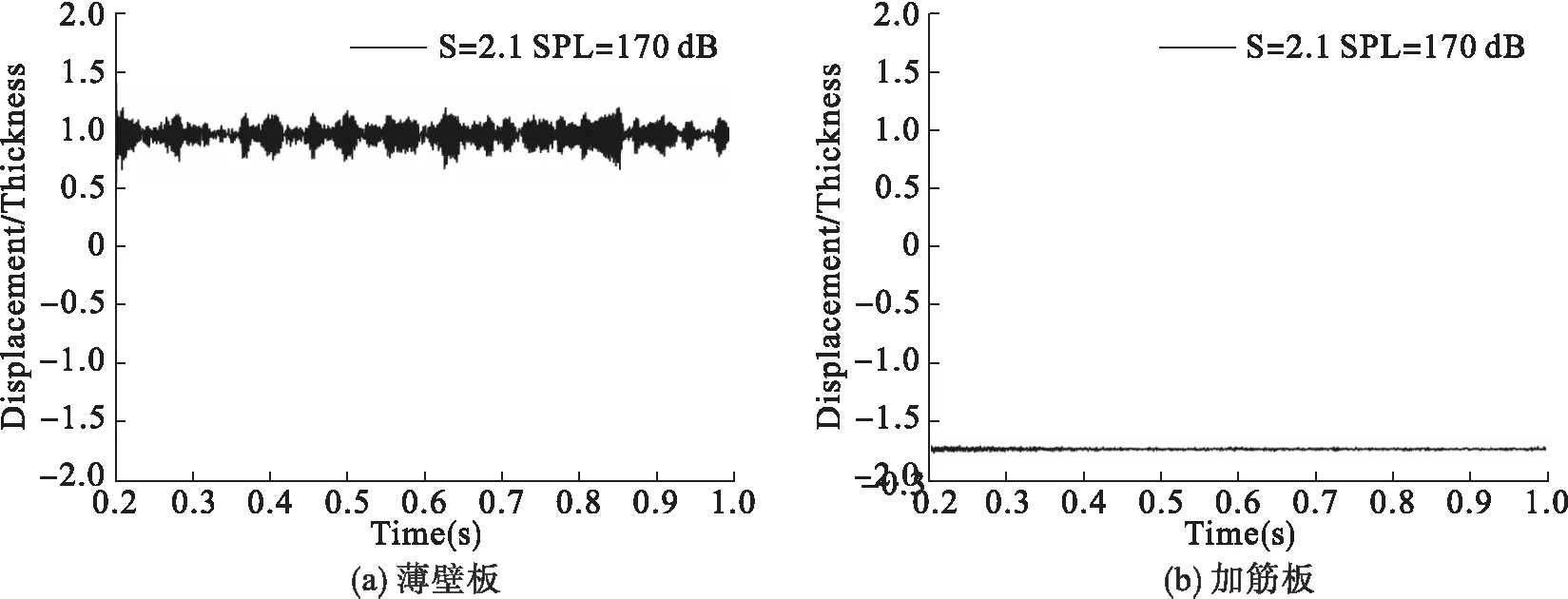
图6 板中心点位置处横向位移时间历程图(S=2.1,SPL=170 dB)

表4 薄壁板与加筋板横向位移均方根

不同温度载荷作用下，加筋板的横向位移概率密度分布如图7-图10所示。

图7 加筋板的横向位移概率密度分布图(S=0)

图8 加筋板的横向位移概率密度分布图(S=1)

图9 加筋板的横向位移概率密度分布图(S=1.4)

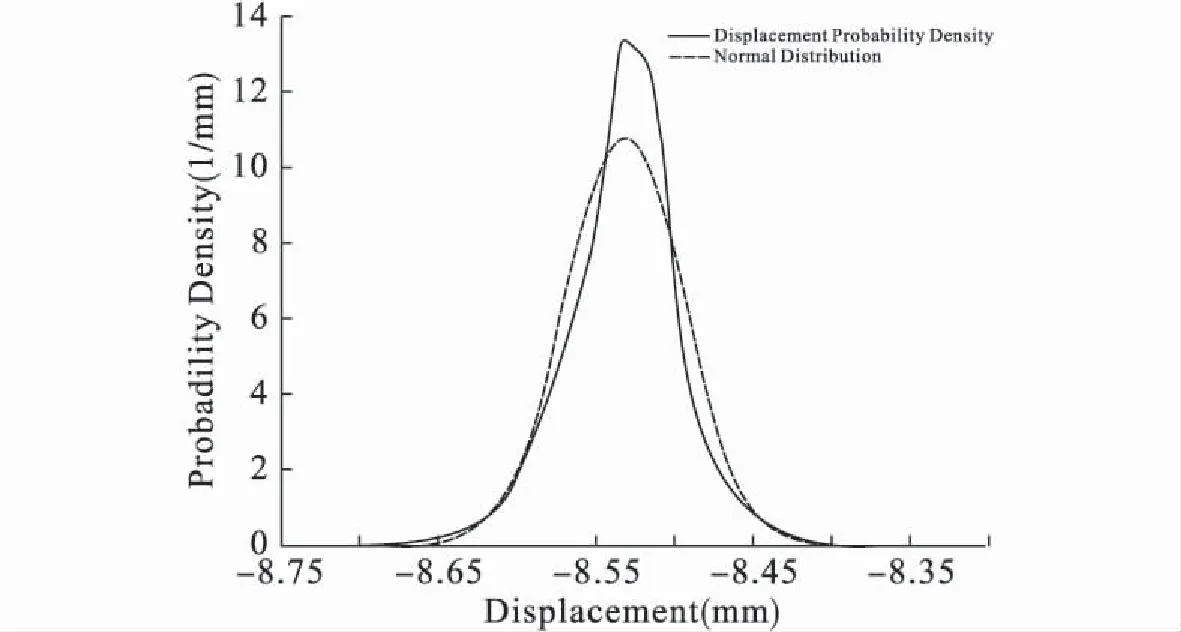
图10 加筋板的横向位移概率密度分布图(S=2.1)

热声激励下，位移响应概率密度分布不再服从高斯分布，随着温度载荷的增加，位移概率密度分布变化较大，没有一定的规律性。屈曲系数S=1.4时，位移概率密度分布具有“双峰”特点，当跳变运动消失后，位移概率密度分布再次呈“单峰”状。

3 结论

本文采用FEM研究了热声激励下薄壁光板和加筋板的动态响应特性，计算了四边简支铝合金薄壁板与加筋板在同一声压级，不同温度下的大挠度随机响应，通过分析比较可知：

(1)热声载荷作用下，薄壁结构具有复杂的动态响应形式，包括屈曲前围绕初始平衡位置的随机振动，屈曲后的跳变运动，以及屈曲后围绕一个平衡位置的随机振动，严重影响着结构的疲劳寿命；

(2)热声激励作用下，加筋板进行大挠度非线性运动，位移响应概率密度分布不再服从高斯分布,并随温度上升作无规则的变化；

(3)计算了四边简支铝合金薄壁板与加筋板在同一声压级，不同温度下的大挠度随机响应，加筋板的热屈曲温度明显高于薄壁平板，且相同载荷环境下，加筋板结构的应力水平较低，振幅较小，承受载荷能力更强。

参考文献(References)：

[1] 沙云东,郭小鹏,廖连芳,等.随机声载荷作用下的复杂薄壁结Von Mises应力概率分布研究[J].振动与冲击,2011,30(1):137-141.

[2] McEwan,M I,Wright,J R,Cooper,J E,et al.A Finite Element/Modal Technique for Nonlinear Plate and Stiffened Panel Response Prediction[R].AAIA-2001-15955-2001.

[3] 张涛,刘土光,赵耀.加筋板大挠度弯曲变形分析[J].中国造船,2001,42(2):40-47.

[4] 沙云东,闻邦椿,屈伸.薄壁板在随机声载荷作用下的振动响应谱估算[J].振动与冲击,2007,26(6):63-66.

[5] Rizzi.S A,Robinson.J H,Chiang C K.Dynamic Response and Sonic Fatigue Analysis at NASA Langley for Hypersonic Vehicle Structures[R],AIAA-92-5019.

[6] 张洪波.加筋板结构稳定优化设计研究[J].山西建筑,2011,37(3):44-45.

[7] Mei C,Prasad C B.Effects of Nonlinear Damping on Random Response of Beams to Acoustic Loading:the Proceeding of Structures,Structural Dynamics and Materials Conference,27th,San Antonio,TX,May，19-21,196[C].AIAA,1986.

[8] Ng C F,Clevenson S S.High-Intensity Acoustic Tests of a Thermal Environments[J].Journal of Aircraft 1991,28(4):275-281.

[9] Ng C F.Design Guide for Predicting Nonlinear Random Response(Including Snap-through)of Buckled Plates,NASA-CR-181877[R].Old Dominion University,1989.

[10] SHA Yundong,WEI Jing,GAO Zhijun.Nonlinear response and fatigue life prediction of thin-walled structures under thermo-acoustic loadings[J].Applied Mechanics and Materials,2012,157-158:1204-1211.

[11] 沙云东,闻邦椿,屈伸,等.航空薄壁结构在随机噪声载荷作用下的振动响应研究[J].机械制造,2006,45(509):23-26.

[12] 李纪永,沙云东,唐金,等.声载荷作用下高温薄壁结构响应特性分析[J].沈阳航空工业学院学报,2010,27(5),23-28.

[13] SHA Yundong,GAO Zhijun,XU Fei.Influences of thermal loads on nonlinear response of thin-walled structures in thermo-acoustic environment[J].Applied Mechanics and Materials,2012,105-107:220-226.

[14] 张涛,刘土光,周晶晶,等.受面内冲击载荷下加筋板的非线性动态屈曲[J].固体力学学报,2003,24(4):391-398.

[15] Tzou H S,Zhou Y H.Nonlinear piezo thermal elasticity and multi-field actuation,Part2;Control of nonlinear defection buckling and dynamics[J].Transaction of the ASME:The Journal and Acoustics,1997,119：382-389.

[16] 张春月,沙云东,王英.航空薄壁板结构高温声疲劳分析[J].航空发动机，2008,34(2):22-26.