异形截面轴心受压铝合金构件屈曲性能试验研究

王培军，黄 权，管谟达，王 康，邱学军，孙鲁鲁

（山东大学 土建与水利学院，济南 250061）

铝合金构件的截面设计，需同时考虑其结构性能和围护性能。从结构性能方面要求构件有足够的承载能力，防止构件发生整体屈曲，畸变屈曲和局部屈曲；从围护性能方面要求构件的截面设置与围护材料如FRP采光板等直接连接的槽口，截面由许多开口板件和闭口板件等组成，如图1所示，受力性能非常复杂。在20世纪70年代，欧洲钢结构协会（ECCS）和美国铝业协会就已经分别制定了《欧洲铝合金结构建议》［1］和《铝合金结构规范》［2］。中国近年也对铝合金结构进行了一系列的研究。沈祖炎等［3］对中国铝合金结构研究现状作了简述。郭小农等［4－5］对铝合金构件的稳定问题进行了理论和试验研究，石永久等［6］对铝合金受弯构件进行了试验和理论研究，张铮等［7］研究了H型铝合金压弯构件平面内的稳定承载力，王元清等［8］对铝合金均匀受压板件的屈曲问题作了探讨，但其研究对象的截面类型是圆管、H型及槽型，对其他截面形状更复杂的异形截面构件尚缺乏相关研究成果。

图1 常见铝合金构件截面

异形截面铝合金轴压构件，根据构件端部约束条件、截面形式、截面尺寸、构件长度不同，除发生常见的局部屈曲、整体弯曲屈曲和整体扭转屈曲外，还易发生畸变屈曲。畸变屈曲指截面中带卷边翼缘与腹板的交线发生转动，导致截面形状的改变，但腹板与翼缘间的角度保持不变，从而腹板产生局部弯曲变形，构件沿纵向出现类似于局部屈曲的畸变屈曲变形。腹板和翼缘以相同的屈曲半波弯曲，卷边和翼缘的交线不再为直线。畸变屈曲波长介于局部屈曲和整体屈曲波长之间。目前与薄壁构件相关的规范除了对局部屈曲和整体屈曲有较为详尽的描述且有相关设计公式［2，9］外，对畸变屈曲却缺乏系统研究。相关的试验和理论分析［10－11］表明，对某些截面畸变屈曲是控制承载力的决定因素。姚行友和李元齐等［10］的试验研究表明，冷弯薄壁型钢卷边槽形截面在轴压作用下可能发生畸变屈曲，郑敦和余绍锋［11］研究了开孔薄壁卷边槽钢的畸变屈曲性能；罗洪光等［12］提出了计算薄壁卷边槽钢的畸变屈曲承载力的直接强度法；Luo等［13］研究了薄壁槽型截面构件绕弱轴的弯曲时的畸变屈曲性能；Nandini等［14］，Camotim 和 Dinis［15－16］研究了局部屈曲、整体屈曲和畸变屈曲的相关作用。当发生畸变屈曲时，会导致构件承载能力明显降低并危及结构的整体安全，因此需对薄壁构件的畸变屈曲进行系统的试验研究和数值模拟。

本文对异形截面铝合金构件在轴向压力作用下的屈曲性能进行了试验研究，为安全经济设计铝合金结构提供实验数据。并对试验结果进行了有限元模拟，以验证有限元模型的正确性。

1 试验研究

异形截面铝合金构件轴心受力试验采用50t液压伺服试验机进行，轴力大小及构件轴向变形试验机自动记录。试验构件材料为6063铝合金，由铝棒通过模具热拉拔而成（T5状态）。

1.1 轴心受拉试验研究

为确定试验构件所用铝合金的材料性能，对图2所示截面的铝合金构件进行拉伸试验（T01a和T01b），试验后构件变形如图3所示，断口处有明显的颈缩现象，表明6063（T5）铝合金材料具有良好的塑性性能。材料的弹性模量和强度的试验结果见表1。屈服强度最小值为193.1MPa，大于《铝合金结构设计规范》（GB 50429—2007）［9］给出的屈服强度设计值150MPa；弹性模量为67.1GPa，小于《铝合金结构设计规范》［15］给出的屈服强度设计值70GPa。应力应变关系如图4所示，表明铝合金材料具有良好的塑性性能。

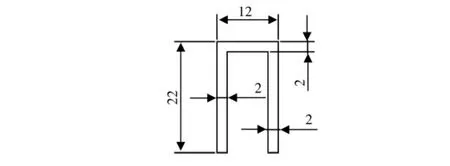
图2 拉伸试验构件

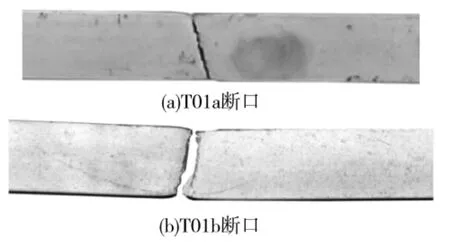
图3 铝合金受拉构件断口处变形

表1 轴心受拉试验结果

图4 铝合金材料的应力应变关系

1.2 轴心受压试验研究

对图1所示截面铝合金构件在轴压作用下的屈曲性能进行了试验研究，并通过设置不同方向的初弯曲，使构件产生不同的屈曲破坏模式。限于篇幅，本文仅给出截面B构件的试验结果。构件长度350mm，共进行了4次试验。试验结果见表2；构件轴力轴向变形曲线如图5所示；试验后构件变形如图6所示。

试验构件为开口截面且无对称轴，在轴压作用下发生扭转屈曲和畸变屈曲。轴力达到极值点前，随着轴向变形的增加，轴力逐渐增加；当轴力达到极值点时，构件发生屈曲，轴向变形继续增大，但为维持构件的平衡状态，必须减小轴力。随着轴力的增加，试件截面中的悬臂板件首先发生局部屈曲；同时悬臂板件绕板件交线扭转，截面形状改变，即发生畸变屈曲；随后构件挠度突然增大，发生整体的弯扭屈曲，轴力达到最大值。构件的轴力轴向变形曲线如图5所示。由于构件长度仅为350mm，上述板件局部屈曲、截面畸变屈曲和构件整体屈曲基本同时发生。试验构件的屈曲变形如图6所示。构件的屈曲方向对承载力基本无影响，试验构件B01和B04弯曲方向为Y＋方向，屈曲承载力平均值为64.2kN；构件B02和B03弯曲方向为Y＋方向，屈曲承载力平均值为68.2kN。两者基本相同。构件屈曲方向和屈曲承载力试验结果见表2，可偏安全取试验构件的屈曲荷载为63.1kN。

表2 屈曲承载力

图5 轴力竖向变形曲线试验与有限元分析结果

2 数值模拟

利用有限元程序ABAQUS对试验构件进行模拟，构件编号见表3，铝合金应力应变关系采用图4所示的试验结果，数值分析采用位移加载模式。轴心受压构件非线性屈曲分析时，需引入初弯曲；且如果初弯曲过小，构件仅发生强度破坏，如果初弯曲过大，导致屈曲荷载计算值偏低。有限元分析模型通过调整初弯曲大小，综合考虑以上各缺陷。初弯曲大小参数敏感性分析表明，当最大初始弯曲小于0.1mm时，构件仅发生强度破坏。取最大初始缺陷为0.7mm，并通过调整节点坐标引入初始几何缺陷。单元采用S4R壳单元，网格大小为5mm×5mm。有限元模型中构件两端分别设置刚性加载板模拟压力试验机的实际加载过程。加载板与构件端部采用ABAQUS的接触算法。采用位移加载法求解构件非线性屈曲轴力轴向变形曲线。

图6 试验构件B01～B04试验后变形图

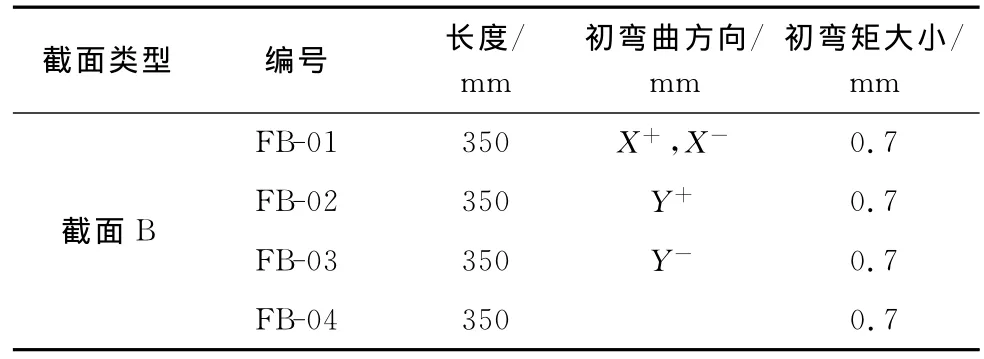
表3 有限元模拟轴心受压构件编号

构件屈曲变形的有限元模拟结果如图7所示，同时包含局部屈曲，整体屈曲和畸变屈曲。与图6试验结果一致。屈曲后截面变形的模拟结果如图8所示，截面既有整体弯曲和扭转，也有板件的局部弯曲和扭转，因此对异性截面铝合金构件的承载力计算，必须考虑各种破坏模态，以及破坏模态之间的耦合作用。表4给出了截面B构件屈曲承载力的有限元分析结果，初弯曲方向对构件的屈曲承载力无影响。但初弯曲方向对构件屈曲时的截面应力分布有显著影响，如图9所示。初弯曲方向为X轴正向、X轴负向和Y轴正向时，构件受压板件明显发生了局部屈曲。

图7 FB－01、FB－02、FB－03、FB－04变形有限元分析结果

图8 构件畸变屈曲后跨中截面的变形

图9 构件屈曲时截面应力分析结果

3 规范公式承载力计算及比较

采用《铝合金结构设计规范》［9］给出的轴压构件承载力的计算方法，该计算方法未考虑局板件局部屈曲和截面畸变屈曲的影响。截面B构件轴心受压屈曲承载力的计算结果见表5。表5同时给出了截面B构件屈曲承载力的试验结果与有限元分析结果。《铝合金结构设计规范》［9］低于试验结果和有限元模拟结果，两者相差约10%。规范对本文所研究的异形截面铝合金构件没有区分屈曲破坏类型的影响，屈曲承载力的计算结果偏小；有限元分析结果与试验结果吻合较好，可用于后续异形截面铝合金屈曲性能的参数分析。

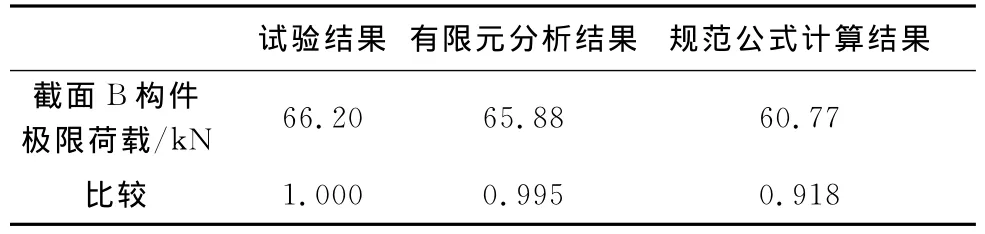
表5 轴心受压铝合金构件屈曲承载力比较

4 结 论

1）给出了图1所示B截面构件屈曲性能的试验和有限元分析结果。由于组成截面的开口板件和闭口板件不同，导致不同板件边界支撑条件不同，影响各板件屈曲发展过程。与B截面试件相比，截面A、C和D试件发生板件局部屈曲和截面畸变屈曲后，轴力仍可持续增加，随后发生整体弯扭屈曲，构件发生破坏。

2）将B截面构件屈曲性能的试验结果，数值模拟结果以及《铝合金结构设计规范》中相关公式的计算结果进行了对比。结果表明，数值模拟可以准确计算异形截面铝合金构件的屈曲承载力。薄壁铝合金构件可能发生整体屈曲，局部屈曲和畸变屈曲，且各屈曲破坏模态可能同时存在。规范对本文所研究异形截面铝合金构件没有区分屈曲破坏类型的影响，屈曲承载力的计算结果偏小。

［1］Aluminum association.Specification for aluminum structures［S］.1st ed.London，1976.

［2］ECCS.European recommendations for aluminum alloy structures［S］.1st ed.London，1978.

［3］沈祖炎，郭小农，李元齐.铝合金结构研究现状简述［J］.建筑结构学报，2007，28（6）：100－109.Shen Z Y，Guo X N，Li Y Q.State－of－arts of research of aluminum alloy structures ［J］.Journal of Building Structures，2007，28（6）：100－109.

［4］郭小农，沈祖炎，李元齐，等.铝合金受弯构件理论和试验研究［J］.建筑结构学报，2007，28（6）：129－135，146.Guo X N，Shen Z Y，Li Y Q，et al.Theoretical and experimental research on aluminum alloy beams［J］.Journal of Building Structures，2007，28（6）：129－135，146.

［5］郭小农，沈祖炎，李元齐，等.铝合金偏心受压构件理论和试验研究［J］.建筑结构学报，2007，28（6）：136－146.Guo X N，Shen Z Y，Li Y Q，et al.Theoretical and experimental research on aluminum alloy members under eccentric compression ［J］.Journal of Building Structures，2007，28（6）：136－146.

［6］石永久，王元清，程明，等.铝合金梁中腹板受弯屈曲的设计方法［J］.土木建筑与环境工程，2009，31（4）：1－5.Shi Y J，Wang Y Q，Cheng M，et al.Design method for bending buckling of web in aluminum beam［J］.Journal of Civil，Architectural ＆ Environmental Engineering，2009，31（4）：1－5.

［7］张铮，张其林.H形截面铝合金压弯构件平面内稳定承载力的试验及理论研究［J］.建筑结构学报，2006，27（5）：9－15.Zhang Z，Zhang Q L.Experimental and theoretical research on in－plane stability capacity of H－section aluminum beam－columns ［J］.Journal of Building Structures，2006，27（5）：9－15.

［8］王元清，石永久，袁焕鑫，等.铝合金板件的受压屈曲分析［J］.武汉大学学报：工学版，2011，44（1）：74－78.Wang Y Q，Shi Y J，Yuan H X，et al.Compressive buckling of aluminum alloy plates ［J］.Engineering Journal of Wuhan University，2011，44（1）：74－78.

［9］中华人民共和国建设部.GB 50429－2007铝合金结构设计规范［S］.北京：中国计划出版社，2007.

［10］李元齐，刘翔，沈祖炎，等.高强冷弯薄壁型钢卷边槽形截面轴压构件畸变屈曲控制试验研究［J］.建筑结构学报，2010，31（11）：10－16.Li Y Q，Liu X，Shen Z Y，et al.Experimental study on distortional buckling control for high－strength coldformed thin－walled steel lipped channel columns subject to axial compression［J］.Journal of Building Structures，2010，31（11）：10－16.

［11］郑敦，余绍锋.开孔冷弯薄壁卷边槽钢畸变屈曲性能分析［J］.建筑钢结构进展，2010，12（4）：32－37.Zheng D，Yu S F.Analysis of distortional buckling performance of cold－formed lipped－channel with perforations［J］.Progress in Steel Building Structures，2010，12（4）：32－37.

［12］罗洪光，郭耀杰，刘华琛.冷弯薄壁轴压柱畸变屈曲直接强度法和有效面积法对比分析［J］.建筑结构，2011，41（2）：56－58 Luo H G，Guo Y J，Liu H C.Comparisons of DSM and EAM of distortional buckling of cold－formed thin－wall columns under axial pressure［J］.Building Structure，2011，41（2）：56－58.

［13］Luo H G，Guo Y J，Ma S C.Distortional buckling of thin－walled inclined lipped channel beams bending about the minor axis ［J］.Journal of Constructional Steel Research，2011，67（12）：1884－1889.

［14］Nandini P，Kalyanaraman V.Strength of cold－formed lipped channel beams under interaction of local，distortional and lateral torsional buckling ［J］.Thin－Walled Structures，2010，48（10／11）：872－877.

［15］Dinis P B，Camotim D.Local／distortional mode interaction in cold－formed steel lipped channel beams［J］.Thin－Walled Structures，2010，48（10／11）：771－785.

［16］Camotim D，Dinis P B.Coupled instabilities with distortional buckling in cold－formed steel lipped channel columns［J］.Thin－Walled Structures，2011，49（5）：562－575.