比特排序的低复杂度K-best检测算法

周 茜，楼喜中，陈燕敏

（中国计量学院 信息工程学院，浙江 杭州310018）

多入多出（multiple-input multiple-output，MIMO）技术是无线通信领域智能天线技术的重大突破.MIMO技术在不增加带宽的情况下成倍地提高通信系统的容量和频谱利用率［1］，是新一代移动通信系统必须采用的关键技术.而MIMO无线通信系统中的信号检测即“MIMO检测”，是MIMO系统研究中不可回避的关键技术问题.如何以尽可能低的检测复杂度，有效地抑制MIMO系统中的同信道干扰并恢复出发送信号，是一项具有挑战性的研究任务.

目前国内外主要的MIMO检测算法有：最大似然（maximum likelihood，ML）检测算法［2］，线性检测算法和树形搜索检测算法等.ML检测算法是通过搜索整个发送信号空间来实现最优的检测性能，但其运算复杂度随调制阶数和天线数目的增多呈指数增长，在实际系统中难以实现.线性检测算法主要包括迫零（zero forcing，ZF）检测算法和最小均方误差（minimum mean-square error，MMSE）检测算法等，这类算法实现原理简单，但性能较差，通常不会单独使用.树形搜索检测算法是利用不同的搜索策略来缩小求解空间，它可以获得接近ML算法的检测性能且算法复杂度较低，因而备受研究者们的关注.常见的树形搜索检测算法主要有：球形译码（sphere decoding，SD）［3-4］算法和 K-best算法［5-6］.SD算法是通过设定一个译码半径r，在以r为半径的球体范围内搜索最优解，如果r的值合适，则会在降低复杂度的同时获得最优的检测性能.SD算法可以采取深度优先策略和广度优先策略进行树形搜索.深度优先策略的SD算法和ML算法性能一致，但不可预测的可变的复杂度使其应用困难；广度优先策略SD算法就是K-best算法.K-best算法不同于传统SD算法的是：它在树形搜索过程中，每一层只保留固定的K条最小路径，从而减小搜索空间、降低计算复杂度.随着搜索范围的扩大，K-best算法也可以获得次优的检测性能，而且具有固定的复杂度的优点使其在实际中被应用成为可能.

通常，K-best算法需要先对每一层的候选路径进行排序，然后从中选出K条最短的路径保留.常用的排序算法有冒泡排序、归并排序和插入排序等，这些算法在硬件实现中需要耗费计算资源和能量比较多.为了降低K-best算法中排序操作的复杂度，本文提出一种基于硬件中比特计数思想的比特排序（bit-sort，BS）算法，该BS K-best算法并不需要对这些路径进行严格次序的排列，它通过依次查找每条路径权重值的各比特位，从而快速的找出所要保留的K条最短路径.此外，在BS算法的基础上，我们又提出了一种动态比特排序（dynamic bit-sort，DBS）算法.该DBS K-best算法不再找出固定的K条最小路径，而是根据当前路径权重值的大小，找出不大于K条的最小路径，从而进一步降低了K-best算法的计算复杂度.

本文的内容安排如下：第一节介绍系统模型，传统的硬判决检测和软判决检测K-best算法；第二节提出改进的BS K-best算法和DBS K-best算法的具体方案；第三节给出相关的仿真结果及计算复杂度的分析；第四节总结全文，提出结论.

1 传统的K-best算法

1.1 系统模型

考虑一个具有Nt根发送天线和Nr根接收天线的MIMO系统，信道为瑞利平坦衰落无线信道，则信道模型可表示为：

通常，将式（1）中的复数模型转化成实数形式y＝Hs＋n表示，即：

1.2 硬判决检测和软判决检测的K-best算法

根据检测器输出信息形式的不同，MIMO检测可分为硬判决检测和软判决检测.硬判决检测是根据欧氏距离最近原则选取距离接收符号最近的星座点作为检测结果，检测器输出的是二进制序列；而软判决检测是计算接收符号对应每个星座点的概率——对数似然比（log likelihood ratio，LLR），然后选取最大后验概率对应的星座点作为检测结果，检测器输出的是表示每位比特为0或1的可能性大小的概率序列.

1.2.1 硬判决K-best检测算法 MIMO硬判决检测就是要查找距离接收信号最近的星座点，将其作为判决结果，即：

将信道矩阵H进行QR分解得到H＝QR，其中Q是一个2 Nr×2 Nt的酉矩阵，R是一个2 Nr×2 Nt且对角元素都是正实数的上三角矩阵；然后将式（2）的左右两端同乘上QT得到：

其中i＝2 Nt…1，距离增量｜ei（s（i））｜2为：

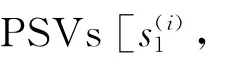
广度优先搜索的K-best球形译码算法树形搜索的顺序是从第2 Nt层依次到第1层.假设当前第i层保留了K 条路径，对应K个则在第i-1层需要对这K个PSVs节点作扩展，每个PSV节点可以扩展出Mc个子节点，这样第i-1层就有了K×Mc条候选路径；利用式（6）计算这K×Mc条路径的PEDs di，然后对这些PEDs（只取球形半径r内部的路径）进行排序，从中选出K条最短的路径保留，其余的路径删除；这样重复以上步骤，直到最后一层i＝1时，同样计算K×Mc个节点的PED，但只从中选出具有最小PED的路径所对应的PSV作为发送信号的估计.

1.2.2 软判决K-best检测算法 软判决MIMO检测是将检测器与信道译码器相结合，检测器根据信道译码器反馈的外信息（对检测器来说是先验信息，记为LA）计算得到外信息LE，并将LE传送给信道译码器用于各对应比特的判决和计算新的LA.

根据贝叶斯定理和最大对数近似的方法，可以得到外信息LE的计算公式：

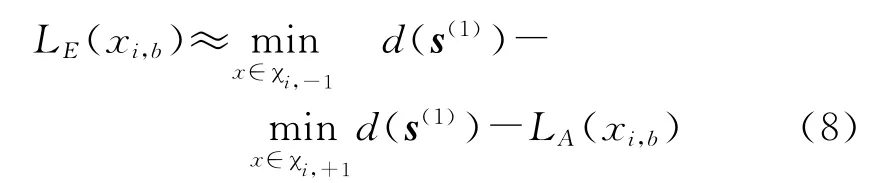
其中xi，b表示第i层的符号xi的第b个比特，且xi，b＝±1，χi，＋1和χi，-1分别表示第i层中xi，b等于＋1和-1的符号集合，i＝1…2 Nt，b＝1／2log2M.d（s（1））可由式（6）和（7）计算得到，LA（xi，b）在第一次迭代时为0.

由式（8）可知，软判决K-best算法与硬判决K-best算法的计算过程十分相似，两者中间的搜索过程基本一致，只在最后一步对输出结果的处理方法有所不同.软判决K-best算法的树形搜索过程从第2 Nt层依次到第1层，每层保留K条最短路径，那么第1层就可以得到K×Mc条路径，最后从这K×Mc条路径集中查找并计算每个比特对应的外信息LE.通常，为确保式（8）中每个比特xi，b对应的 minx∈χi，＋1d（s（1））和 minx∈χi，-1d（s（1））都能查找到，软判决K-best算法要求具有比硬判决K-best算法更大的K值.在最后产生的K×Mc条路径集中，如果所有的路径对应的某个比特均为＋1或-1，那么式（8）中的两个min项就有一个查找不到.此时，可以采取两种近似方法［7］：一种是将第i层第b位xi，b＝＋1（xi，b＝-1）时对应的最大（或最小）PED与最小（或最大）PED相减得到的差值作为该比特的外信息LE（xi，b）；另一种是预先设定一个足够大的LLR值来代替.然而不论哪种近似方法，都会导致检测性能的损失，只有增大K值才能减少引起这种性能损失的概率，系统的检测性能也会越好，但K值越大，检测器需要计算的路径PED数量和PEDs排序操作的次数就越多，从而导致系统的复杂度增加.

从以上硬判决和软判决K-best算法的搜索过程可以看出，算法的复杂度主要集中在PEDs的计算和排序操作上，PEDs的计算复杂度可以通过选择合适的译码半径r来减少所要计算的节点数，这在深度优先SD算法中已经有了很好的改进；对于PEDs的排序复杂度，文献［8］虽然提出在不同层选择不同的K值的方法，但它需要经过多次仿真才能确定最优的K值序列，效果并不够理想.对于调制星座尺寸为Mc的K-best树形检测器，每层需要计算和排序的PEDs数量为K×Mc，当K和Mc增大时，计算的复杂度呈指数形式增长，在硬件上难以实现.

2 改进的K-best排序算法

为了降低K-best算法排序的复杂度，本文提出一种基于硬件中比特计数操作思想的排序算法——BS算法，和一种进一步简化BS算法计算复杂度的动态排序算法——DBS算法.这两种方法均可以用在硬判决K-best算法和软判决K-best算法中.

2.1 改进的BS算法

在该BS算法中，每条路径的PED以二进制的形式存储在一个长度N的寄存单元中，通过查找每条路径PED的比特值，从而快速地找出K条最短路径.PEDs的存储结构如图1所示.

图1中的比特个数N的值是由PEDs的大小和所采用的量化方法决定的.该BS算法从每个存储单元的最高位比特bN-1开始依次向低位比特查找，直到找出K条最短路径.假设当前查找到了第n个比特bn，候选路径的数量为L条，其中bn＝0对应的路径数量为kn，需要保留的最短路径数量为k（0＜k≤K）条.初始时，n＝N-1，k＝K，L＝k×Mc，则BS K-best算法查找K条最短路径的步骤如下.

图1 PEDs的存储形式Figure 1 Storage structure of PEDs

a）查找L条候选路径的PEDs的第n个比特bn，并选出比特bn＝0的路径，其数量记为kn（kn≥0）.

b）根据kn的大小分类考虑：

如果kn＝0，则更新n＝n-1，然后判断：若n≥0，返回a）继续查找，否则跳至c）；

如果kn＞k，则删除bn＝1的路径，将选出的kn条路径作为新的查找范围，并更新L＝kn，n＝n-1，然后判断：若n≥0，返回a）继续查找，否则跳至c）；

如果0＜kn＜k，则保留选出的kn条路径为所要查找的K条最短路径的一部分，并将bn＝1的路径作为新的查找范围，更新k＝k-kn，L＝kn＋1-kn，n＝n-1，然后判断：若n≥0，返回a）继续查找，否则跳至c）；

如果kn＝k，则保留选出的kn条路径到所要查找的K条最短路径中，然后结束该BS算法.

c）此时认为剩余的L条路径的PEDs相等，从中任意选取k条保留，然后结束该BS算法.

从以上步骤可以看出，BS K-best算法通过对PEDs的比特值查找并计数，可以快速的找出K条最短路径，并不需要对候选路径进行严格的次序排列，这样就大大降低了传统K-best算法中排序操作的复杂度.该BS K-best算法的比特计数操作次数主要由PEDs的比特位数N决定，最坏的情况是需要执行N次比特计数操作.通常，所有天线上的发送符号都做了归一化处理，因此PEDs的值都比较小，N的值也就比较小，但随着调制阶数的增大，求解空间的星座点更加密集，所需要查找的比特位数会有所增加.

2.2 改进的DBS算法

在BS算法中，当0＜kn＜K时，当前的kn条最短路径保留，然后需要再查找其余的K-kn条最短路径，这样会增加新的计算量，因此我们又提出一种动态比特排序（DBS）算法来简化这部分计算量.在DBS算法中，假设符号L和kn与BS算法中的L和kn具有相同的意义和初始值，则该DBS K-best算法查找不大于K条最短路径的步骤如下.

a）查找L条候选路径的PEDs的第n个比特bn，并选出bn＝0的路径，其数量记为kn.

b）根据kn的大小分类考虑：

如果kn＝0，则更新n＝n-1，然后判断：若n≥0，返回a）继续查找，否则跳至c）；

如果kn＞K，则删除bn＝1的路径，将选出的kn条路径作为新的查找范围，并更新L＝kn，n＝n-1，然后判断：若n≥0，返回a）继续查找，否则跳至c）；

如果0＜kn≤K，则保留当前选出的kn条路径为所要查找的最短路径，然后结束该DBS算法.

c）此时认为剩余的L条路径的PEDs相等，从中任意选取K条保留，然后结束该DBS算法.

从以上步骤可以看出，当0＜kn＜K 时，该DBS算法只保留当前kn条最短路径并结束算法，不再查找其余的K-kn条路径.因此，DBS K-best算法通过保存动态的K条路径简化了需要保存固定K条路径的传统K-best算法和BS K-best算法的计算复杂度.另外，在K-best树形搜索中，最后一层（第i层）不再保留K条路径，而是只保留最短的一条路径，因此，为了降低计算复杂度，我们先用DBS算法找出最后一层的动态K条最短路径，然后再用传统排序算法从这动态K条路径中找出最短的一条.

3 仿真与分析

采用4×4收发天线，64-QAM和16QAM调制，5／6码率的 Turbo信道编码，Bahl Cocke Jelinek Raviv（BCJR）译码，TGn C类信道模型的MIMO系统［9-10］.信道矩阵 H 采用sorted-QR（SQR）分解，每根接收天线上的信噪比（signalto-noise，SNR）SNR＝NTEs／N0，其 中 Es＝E［｜sk｜2］（∀k），E［·］代表取期望值.

3.1 算法的性能

图2和图3分别给出了16-QAM和64-QAM调制下SD算法、BS K-best算法和DBS K-best算法硬判决检测时的误码率（BER）曲线.图4和图5分别给出了16-QAM和64-QAM调制下以上三种算法软判决检测时的BER曲线.本文提出的BS K-best算法和DBS K-best算法是对路径权重PEDs排序的过程进行简化，其BER性能和传统K-best算法的一致，没有性能损失，因此仿真图形中不再给出传统K-best算法的BER曲线.另外，以下仿真中，将次优的硬判决SD算法和软输入软输出（SISO）单树搜索（STS）SD算法的BER曲线作为K-best算法性能的参考标准.

图2 16-QAM调制时硬判决检测算法的BER性能Figure 2 BER performance of hard decision detection algorithm in 16-QAM constellation

图3 64-QAM调制时硬判决检测算法的BER性能Figure 3 BER performance of hard decision detection algorithm in 16-QAM constellation

图4 16-QAM调制时软检测算法的BER性能Figure 4 BER performance of SISO detection algorithm in 16-QAM constellation

图5 64-QAM调制时软检测算法的BER性能Figure 5 BER performance of SISO detection algorithm in 64-QAM constellation

从图2中可以看出，随着K值的增大，BS K-best算法和DBS K-best算法的BER性能都越来越好.当K＝16时，BS K-best算法和DBS K-best算法的BER曲线均与硬判决SD算法的曲线基本重合，即这两种算法的性能都达到了稳定，即使再增大K值也不会有性能的提升了.图3中64-QAM调制时，同样，K值越大，两种改进的K-best算法的性能越好.当K＝48时，BS K-best算法可以得到与硬判决SD算法一致的BER性能，而DBS K-best算法的性能还有一定的损失，需要K≤64时才能与硬判决SD算法一致.因此，BS K-best算法和DBS K-best算法在合适的K值下均可以达到次优的硬判决SD算法的BER性能.

由图4和图5中可知，由于信道译码的增益，在BER＝10-5时，16-QAM和64-QAM调制下，同样K值的BS K-best软判决算法比硬判决算法分别有8.2dB和7.5dB的性能提升；SISO K-best检测第三次迭代后的BER曲线比第一次迭代后的BER曲线性能提升大约0.5～2dB，且K值越大、调制阶数越高提升越明显.在16-QAM和64-QAM调制时，硬判决BS K-best算法分别在K＝16和K＝48时已逼近次优的硬判决SD算法的BER性能，而软判决BS K-best算法的性能还有非常大的提升空间，随着K值的继续增大，硬判决检测的性能保持稳定，软判决迭代检测的性能将会显著提高.但是由于K-best树形搜索每层只保留K条路径，软判决K-best算法需要足够大的K值才能逼近次优的软输出SD算法的性能.

3.2 算法的复杂度

在传统的K-best算法中，需要进行一个（s，t）的排序操作：从t个元素中选出最小的s个元素，这个过程至少需要t-s＋∑t＋1-s＜j≤tlog2j■ 次元素的成对比较操作.而BS K-best算法和DBS K-best算法是通过对PEDs的比特位进行计数，从而快速的找出最短的K条路径，所需的比特计数操作次数主要由PEDs和K值的大小决定.通常，在硬件操作中，比特计数操作要比元素成对比较操作要简单的多.

在软判决 K-best算法中，式（8）中的一个min项由最后第i＝1层的最短路径（和硬判决K-best算法的一致）决定，另一个min项的查找相当于每次在（K×Mc-1）个数据集中查找一个最大值或最小值，其复杂度并不高，因此，以下只讨论硬判决BS K-best算法和DBS K-best算法的复杂度与传统K-best算法的比较.表1给出了16-QAM（Mc＝4）和64-QAM（Mc＝8）调制时，不同K值的传统K-best算法，硬判决BS K-best算法和DBS K-best算法中每一层找出K条最短路径所需要的搜索复杂度.

表1 复杂度分析Table 1 Complexity analysis

表1中的数据表明，传统K-best算法要从K×Mc条候选路径中找出K 条最短的路径需要花费较多次数的元素比较操作，且K值越大、调制阶数越高，所需要的比较次数就越多.本文提出的BS K-best算法和DBS K-best算法所需要的比特计数次数也会随着K值和调制阶数的增大而增多，但他们所需要的比特计数次数远远小于传统K-best算法的元素比较次数，从而大大降低了K-best算法的搜索复杂度.另外，在第i＝1层，我们先采用BS算法（或DBS算法）快速地找出K（或≤K）条最短路径，然后再用元素比较的方法找出最短的一条路径作为发送信号的估计，这样可以有效的降低第i＝1层的搜索复杂度.在DBS K-best算法中，当算法第一次计数到小于或等于K条路径时就结束了搜索，因此它所需要的比特计数操作计数比BS K-best算法更少.此外，DBS K-best算法保留的动态K条路径数量的均值要比固定的K 值小，例如：16-QAM调制K＝16时，K均值为12.26；64-QAM调制K＝64时，K均值为44.93，所以DBS K-best算法进一步降低了BS K-best检测算法的计算复杂度.

4 结 语

本文针对MIMO系统中，当采用了较多天线或高阶调制时，K-best检测算法为保证性能而引入的大量复杂度问题进行探讨.为了降低K-best算法中候选路径排序的复杂度，我们提出了一种基于硬件中的比特计数思想的BS K-best算法和一种基于BS K-best算法的DBS K-best算法.仿真结果和复杂度分析表明，在K取值合适时硬判决BS K-best算法和DBS K-best算法都可以达到次优的硬判决SD算法的检测性能，软判决K-best算法的性能随着K值的增大而不断改善，且它们都大大降低了传统K-best算法的计算复杂度；此外，DBS K-best算法通过选择动态的K条最短路径，进一步简化了BS K-best算法的计算，更加有利于MIMO系统中K-best检测算法的硬件实现.

［1］Telatar I E.Capacity of multi-antenna Gaussian channels［J］.European Transactions on Telecommunications，1999，10（6）：585-595.

［2］Zhu Xu，Murch R D.Performance analysis of maximum likelyhood detection in a MIMO antenna system［J］.IEEE Transactions on Communications，2002，50（2）：187-191.

［3］Studer C，Burg A，Bolcskei H.Soft-output sphere decoding：Algorithms and VLSI implementation ［J］.IEEE Journal on Selected Areas in Communications，2008，26（2）：290-300.

［4］Studer C，Bolcskei H.Soft-input soft-output single treesearch sphere decoding［J］.IEEE Transactions on Information Theory，2010，56（10）：4827-4842.

［5］Guo Zhan，Nilsson P.Algorithm and implementation of the K-Best sphere decoding for MIMO detection［J］.IEEE Journal on Selected Areas in Communications，2006，24（3）：491-503.

［6］Shabany M，Gulak P G.Scalable VLSI Architecture for KBest lattice decoders［C］／／IEEE International Symposium on Circuits and Systems（ISCAS）2008.Seattle，WA：IEEE Press，2008：940-943.

［7］鞠春晖.高性能软输出K-BestMIMO检测器的设计与实现［D］.上海：上海交通大学，2012.Ju Chunhui.Design and implementation for high performance soft-output K-best MIMO detector［D］.Shanghai：Shanghai Jiaotong University，2012.

［8］Jin Ning，Jin Xiaoping，Ying Yingguo，et al.Research on low-complexity breadth-first detection for multiple-symbol differential unitary space-time modulation systems［J］.IET Communications，2011，5（13）：1868-1878.

［9］Erceg V，Schumacher L，Kyritsi P，et al.IEEE 802.11-03／940r4，TGn channel model［M／OL］.New York：IEEE Press，（2004-05-10）［2007-10-09］.http：／／www.ece.arizona. edu／～ yanli／files／11-03-0940-04-000n-tgn-channelmodels.doc.

［10］Studer C.SISO＿sim＿v1.01［DB／OL］.Houston：Rice U-niversity.（2011-06-25）［2012-03-10］.http：／／www.ece.rice.edu／～cs32／software＿sisostssd.html／SISO＿sim＿v1.01.zip.