80°／65°双三角翼滚转稳定特性预测研究

陶 洋，赵忠良，李 浩，杨海泳，李玉平

（中国空气动力研究与发展中心 空气动力学国家重点试验室，四川 绵阳 621000）

0 引 言

大后掠机翼在大迎角飞行时由于滚转阻尼下降、飞行器前体涡、侧缘涡诱导、气动力非线性、气动力滞后和激波诱导的分离等都会诱发机翼摇滚（wing rock）或其他非指令的自激运动，同时由于纵横向自由度的耦合，严重影响了飞机的安全性和操纵性，大大限制了飞行器的机动性和敏捷性发挥［1-3］。

本研究旨在加深现代飞机大迎角飞行时的滚转特性及相应的流动机理的理解。用80°／65°双三角翼模型作为现代飞机边条翼加大后掠机翼构型的简化模型。探索通过飞行器的定常／准定常气动力数据对飞行器阻尼振幅衰减、机翼摇滚、分叉等滚转特性预测的方法判据。

分别通过静态测力试验及动导数试验获得了双三角翼模型在大迎角条件下的滚转力矩特性以及动导数特性，从而对双三角翼大迎角条件下的滚转运动特性进行了预测，最后通过自由摇滚试验对预测结果进行了验证。

1 试验设备和模型

1.1 风洞

试验在中国空气动力研究与发展中心FL-23风洞中完成。FL-23风洞系试验段横截面为0.6m×0.6m 的半回流暂冲式跨声速风洞。试验马赫数范围为0.3～4.5，马赫数控制精度：±0.005。迎角范围：-10°～50°，试验段上下壁面为开孔率4.2%的60°斜孔壁，两侧为实壁［4］。

1.2 模型

双三角翼模型试验采用尾部支撑，利用中心体与天平连接，中心体外径32mm。为了减轻结构重量及转动惯量，双三角翼模型为铝质（LC4）材料加工，其底边边长200.88mm，厚度6mm。模型净重0.807kg，体轴的摇滚主惯性矩为3.2×10-4kg·m2。具体模型参数见表1。

表1 双三角翼模型主要参数Table 1 The key parameters of the double-delta wing models

1.3 其他设备

自由摇滚装置采用精密机械球轴承支撑，通过联接装置与单支臂大迎角机构相联，通过12位绝对式轴角编码器来测量模型的角位移，测量精度可达0.088°，支撑装置中的微型电磁离合器用于控制模型的锁定及释放，试验数据的采集由PXI-4472B 动态信号采集模块完成，最高采样频率为100K。模型在风洞中的安装情况见图2。

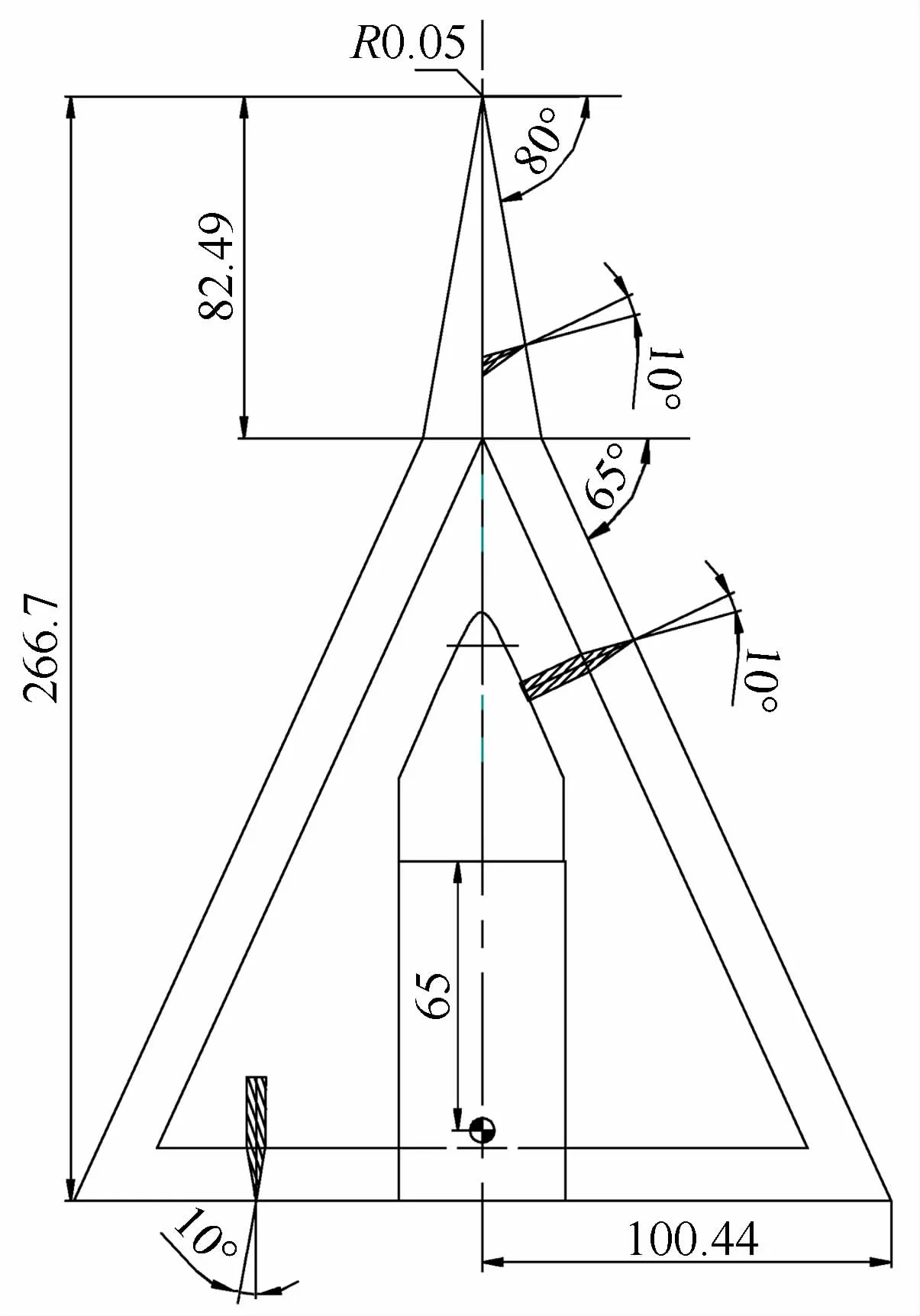
图1 80°／65°双三角翼示意图Fig.1 The schematic of 80°／65°double-delta wing

滚转动导数试验装置采用一台110BC380B步进电机作动力，通过一个机械运动转换机构，将电机的连续转动转换为尾支杆的滚转振动运动，其振动角位移幅值为1.5°，电机转速由计算机、STD 系统控制。动导数测试系统主要包括放大器、数据采集系统等，测试系统采用HP公司基于VXI总线结构的数据采集系统，该系统是完全并行的具有16位分辨率的8通道数据采集模板，其相位误差小于0.1°，能够为各种动导数试验提供可靠的原始数据。

图2 试验风洞及模型Fig.2 The wind tunnel and the testing model

为了提高滚转力矩测量精度，测力及动导数试验采用小滚转力矩量程的五分量天平测量（天平编号2N5-21A），天平量程见表2。

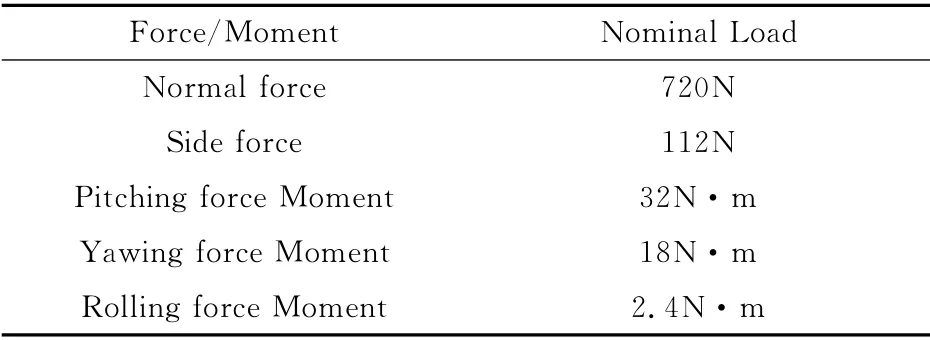
表2 五分量天平Table 2 The nominal loads of 5-components internal force balance

2 试验结果与讨论

2.1 测力试验结果

测力试验条件为马赫数0.3，雷诺数为2.7×105，参考长度为中心体直径。通过静态测力试验获得了不同迎角下的静态滚转力矩系数，具体情况见图3。从图示可见，在迎角20°和25°时，φ=0°附近滚转力矩对滚转角的斜率为负，说明在φ=0°附近模型静态稳定，该点为模型的一个静态平衡点或者摇滚的平衡点，即为一点吸引子或者极限环吸引子。当30°≤α≤35°时φ=0°附近滚转力矩导数大于零，即静导数大于零，所以在该滚转角下模型不稳定，在这些迎角条件下从滚转力矩曲线上判断，过零且斜率小于零的点为稳定点，出现在φ=±15°附近，从而可以判断在φ=±15°附近会出现侧偏的平衡或者侧滚。随着迎角的增加，在38°≤α≤45°区间，整个滚转角范围内，只出现了一个稳定的过零点即φ=0°，所以判断该点为点吸引子或者极限环吸引子。

图3 静态测力滚转力矩系数Fig.3 Static roll moment coefficients

2.2 动导数试验结果

图4给出了双三角翼的动导数结果，从图中可见，φ=0°时在迎角25°以下动导数均小于零，同时从前面的静态测力结果可知在φ=0°处斜率小于零，说明在该状态下模型动稳定且静稳定，从而判断模型在该处的稳定形态为点吸引子。在迎角30°≤α≤35°附近，φ=0°时模型动稳定但静不稳定，说明该点不是一个稳定的平衡点，模型不能稳定在该点或围绕该点做极限环振动，α=40°时，φ=0°处的动导数大于零，同时从测力结果可知φ=0°处的斜率小于零，从而可以判断φ=0°为该迎角条件下的一个极限环吸引子，会出现摇滚运动。

图4 双三角翼动导数（φ=0°）Fig.4 Dynamic stability derivative of double-delta wing

2.3 自由摇滚试验

马赫数0.3时，三角翼的滚转特性随迎角的变化明显分为几个区域，图5为马赫数0.3时双三角翼的滚转角随时间的变化历程。

在迎角小于30°之前，模型是静稳定的，在滚转角0°附近小幅振荡，引起振荡的原因主要是气流的不均匀。在迎角35°时形成具有两个平衡位置的摇滚运动，平衡滚转角位置分别位于±15°附近，在迎角40°形成绕0°平衡位置的摇滚运动，振幅在15°左右。这些状态完全验证了前面通过静态测力结果与动导数试验结果对运动形态的分析。验证了预测方法的正确性。

图5 M=0.3时滚转运动的时间历程Fig.5 Time histories of rolling for M=0.3

图6给出了M=0.3时的相图，形成摇滚后两个典型的状态。35°迎角相图呈现蝴蝶状，40°相图呈准极限环振荡。

图6 M=0.3时滚转运动的相图Fig.6 Phase planes for M=0.3

3 结 论

通过研究得出以下结论：

（1）80°／65°双三角翼模型随迎角的增加，摇滚运动形态为静稳定，多平衡点摇滚，单平衡点摇滚；

（2）通过静态气动力及动导数试验结果可以对双三角翼模型的滚转动态特性进行较好地预测，包括滚转运动形态及对应的迎角范围等，预测结果与自由滚转试验结果吻合良好。

［1］ 刘伟，张涵信.细长机翼摇滚的数值模拟及物理特性分析［J］.力学学报，2005，37（4）：385-392.

［2］ ERISSON L E.Wing rock generated by forebode vortices［J］.J.Aircraft，1989，26（2）：110-116.

［3］ 伍开元，李其畅.面向先进飞行器设计的非定常空气动力学［J］.流体力学实验与测量，1997，11（2）：14-18.

［4］ 樊开导.0.6m×0.6m 跨超声速风洞性能与使用［R］.CARDC-2，1990.

［5］ TREVOR J，BIRCH L.Aerodynamic characteristics of a square cross-section missile configuration at supersonic speeds［R］.AIAA 2004-5197.

［6］ TRICKEY C M，EDWARDS J A，SHAW S.Experimental and computational assessment of the dynamic stability of a supersonic square section missile［R］.AIAA 2004-5454.

［7］ STUART McIlwain，MAHMOOD Khalid.Computations of square and elliptical section missiles using WIND［R］.AIAA 2004-5455.

［8］ 袁先旭.非定常流动数值模拟及飞行器动态特性分析研究［D］.［博士学位论文］.中国空气动力研究与发展中心，2002.

［9］ BURT G E.A description of a forced-oscillation test mechanism for measuring dynamic stability derivatives in roll［R］.AD762258，1973.