基于ARIMA模型上海市生活垃圾的预测与分析
2013-11-15曹昱东
曹昱东,王 浩
(北京师范大学珠海分校,广东珠海,519085)
0 引言
随着经济的不断发展,城市生活垃圾产生量也越来越多,这些生活垃圾严重阻碍了城市的发展,带来了一系列经济、社会、环境问题。全国大部分城市都面临着垃圾快速增长而处理垃圾的设施多年不变的局面。几乎2/3的城市已经被垃圾所包围,而且这种情况日益严峻。城市生活垃圾问题也受到政府的强烈关注,准确的预测未来城市生活垃圾产生量是解决城市生活垃圾问题的第一步,也是关键一步。
1 ARIMA模型介绍
1.1 ARIMA模型的性质
ARIMA模型的全称是求和自回归移动平均模型,ARIMA(p,d,q)模型。使用 ARIMA 模型去做预测,通俗的讲,就是将需要预测的对象随时间变化的数据作为一个随机序列,然后分析出这个序列的特点与性质,从而通过时间序列过去的数值来推测未来的走势。ARIMA(p,d,q)模型具有以下三条性质:
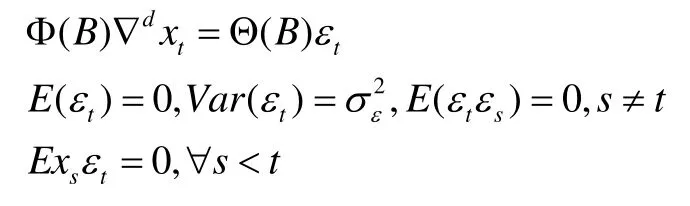
1.2 ARIMA模型的建模步骤
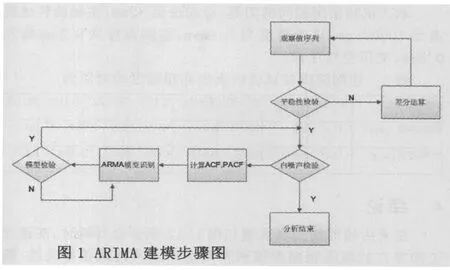
在获取一个观察值序列之后,首先是判断它的平稳性,通过平稳性检验,可以把序列分为平稳序列和非平稳序列两种,要用ARIMA模型进行数据分析,所分析的序列必须是平稳序列,而非平稳的序列则不能直接通过ARIMA模型计算,需要将非平稳序列转化为平稳序列。这里转化的过程就是一种有效提取序列中蕴含的确定性信息的过程。对序列进行差分运算则是一种常用的转化过程。差分运算的实质是使用自回归的方式提取确定性信息。由于差分运算的这种强大提取信息的能力,许多非平稳序列差分之后会显示出平稳序列的性质,对差分后平稳序列可以使用ARIMA模型进行拟合,从而去分析序列的特点。
而具体进行ARIMA模型分析的时候,通过计算ACF,PACF可以有效的确定出ARIMA(p,d,q)中各参数p,d,q的具体数值,从而最终拟合序列并进行预测。具体的ARIMA建模流程图如图1.
2 ARIMA模型在上海市生活垃圾预测中的应用
2.1 数据收集与整理
根据上海市绿化和市容管理局提供的数据,做出1978年到2011年上海市生活垃圾产生量表1。
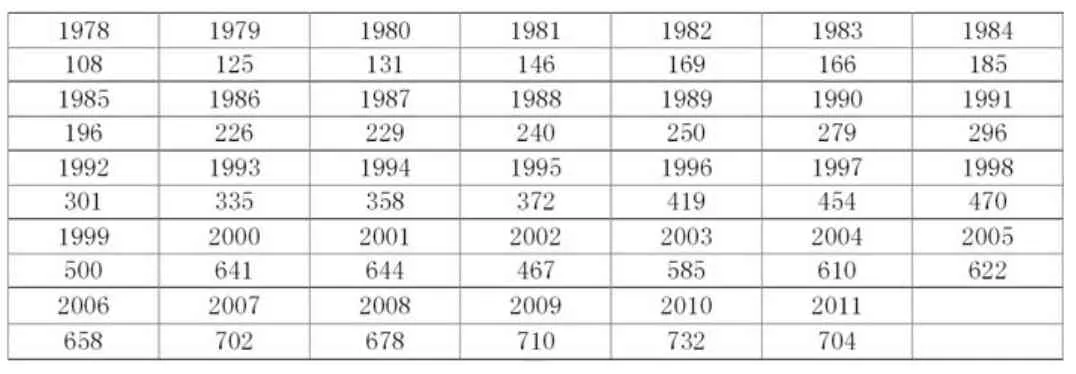
1978到2011年上海市生活垃圾产生量表(单位:万吨)
在SAS软件中,绘制出该序列的时序图图2
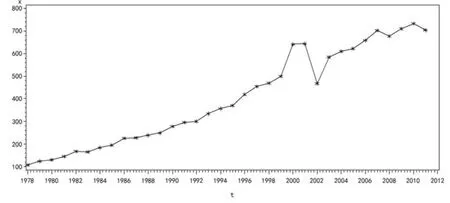
图2:上海市生活垃圾产生量时序图
由图2可看出,随着经济的发展与人口的增加,自1978年来,上海市垃圾产生量大体上呈递增趋势,除了2000年到2002年有一个短暂的回落。垃圾产生量从开始的100万增长到700万,增长的幅度比较块,平均每年增长幅度超过20%。整个图像具有显著的趋势,站在时间序列的角度来说,该序列是典型的非平稳序列。
因为时序图明显非平稳,所以对数据进行一阶差分处理,一阶差分后自相关图和白噪声检验图见图3.

图3:一阶差分自相关、白噪声检验图
由图3可以看出,原序列进过差分运算后,已经向平稳序列方向发展,但是p=0.0341 还是大于标准值0.005,所以我们对该序列继续做差分运算。
进过二阶差分,序列在均值附近比较稳定的波动,白噪声检验如图3。

图3:二阶差分后的白噪声检验图
图3 显示,差分后序列在均值附近比较稳定的波动,p值<0.005,可以认为序列平稳。所以对二阶差分后的数列进行分析。
2.2 ARIMA模型的识别
由偏自相关系数图4可得在延迟期数大于等于4后,偏自相关系数就基本保持在两倍标准差之内。对序列进行相对最优定阶,得到最小信息量结果为图5.
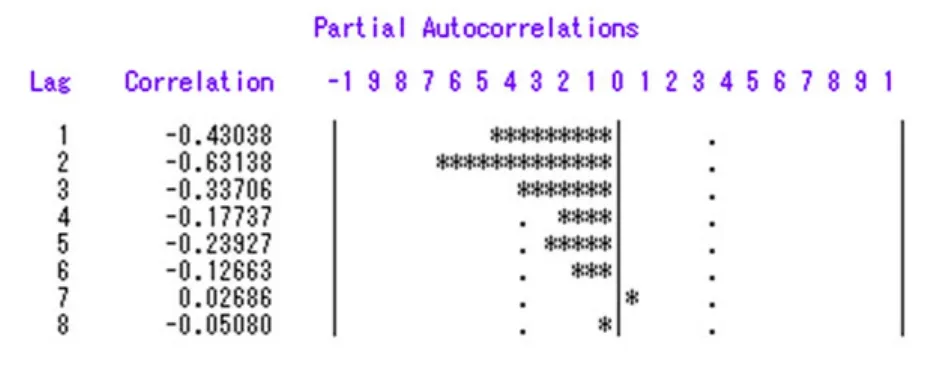
图4:二阶差分后偏自相关图
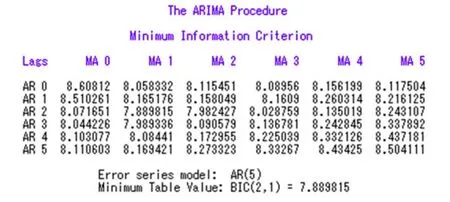
图5:相对最优定价图
图5 显示,在自相关系数小于等于5,移动平均延迟系数小于等于5的所有ARMA(p,q)模型中,BIC信息量相对最小的是 ARMA(2,1)模型,也就是 ARIMA(2,2,1)模型。
2.3 ARIMA模型的检验
对2阶差分后的序列进行残差自相关分析,残差自相关检验结果如图6:

图6:残差白噪声检验图
由于p显然大于0.05,所以残差序列为白噪声序列,拟合模型显著成立,模型检验通过。
所以拟合模型为: 1 + 0.72298B + 0.65197,具体预测数值表2

表2:上海市生活垃圾产生量7期预测(单位:万吨)
最终得到上海市垃圾产生量走势预测图7:
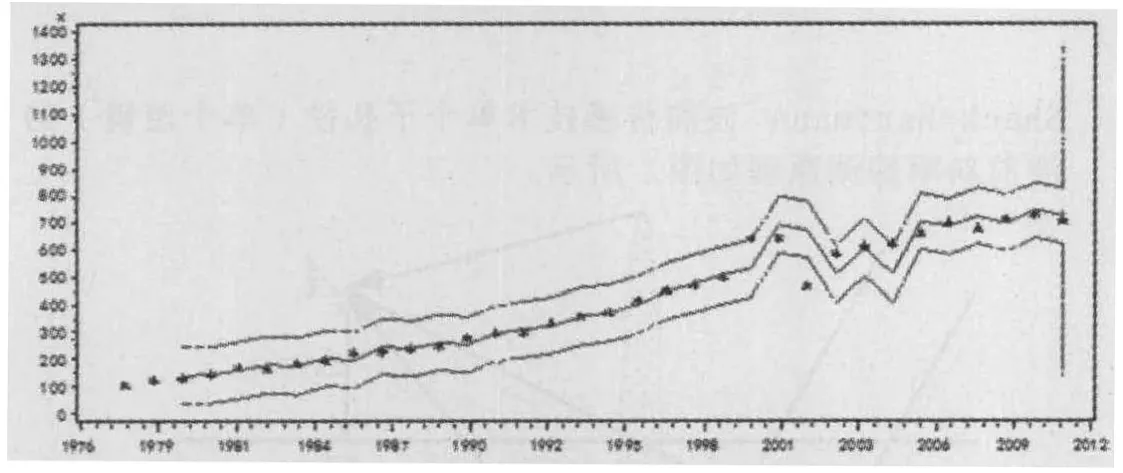
图7:上海市生活垃圾产生量走势预测图
2.4 ARIMA模型优缺点分析
运用ARIMA模型对序列进行预测时,预测的准确度随着时间的推移呈发散的趋势,所以ARIMA模型只适合短期预测。而且由于ARIMA模型基本使用纯数学方法来提取序列中的有效因素,不能从机理上来解释生活垃圾产生量快速增加的原因,从而不利于对垃圾产生做出具体分析,从源头上解决垃圾产生问题。
但是ARIMA模型在预测分析中,理论比较成熟,而且垃圾产生量常常是自相关非平稳的,所以运用ARIMA模型比较合理,且得出的结论可信度较高。
3 结语
垃圾治理问题关系到城市发展的方方面面,是重要的城市建设问题之一。本文通过分析过去几十年的数据,运用ARIMA(2,2,1)模型对上海市未来7年的生活垃圾产生量做了具体的预测,具有一定的应用价值。
[1]徐礼来,崔胜辉,闫祯,等.城市生活垃圾产生预测的核心问题探讨[J].环境科学与技术,2013,36(002):184-190.
[2]芮少权,匡安乐.高速公路月度交通量 ARIMA 预测模型[J].长安大学学报:自然科学版,2010,30(4):82-85.
[3]王燕.应用时间序列分析[M].中国人民大学出版社,2008.
[4]上海统计年鉴:2012[M].中国统计出版社, 2012.
[5]赵鑫,郭嘉,吴建川.ARIMA 模型和 GM (1,1)与 ARMA(p, q)组合模型在滑坡短期预报中的对比分析[J].安全与环境工程,2012,19(3):24-28.
