基于改进BP神经网络的镁还原率预报研究

华建社，薛 臣，刘明华，李 芳

(西安建筑科技大学冶金工程学院，陕西西安 710055)

镁及镁合金具有比刚度和比强度好、导电性和电磁屏蔽性优良、抗震、阻尼性好、节能环保等优良特性，被广泛应用于交通运输工业、航空航天工业、3C产业和精密机械工业等领域，被材料专家誉为21世纪最具开发和应用潜力的绿色工程材料[1-2]。

与铝、塑料等轻量化材料相比，较高的成本限制了镁及镁合金的进一步推广。镁还原率直接影响着镁生产成本，通过优化工艺参数组合提高镁还原率，是镁冶炼工艺研究的一个重要方向。皮江法炼镁工艺生产过程是一个非常复杂的非线性过程，镁还原率的影响因素多，时变性强，机理复杂，很难通过常规的数学模型进行精确描述。

人工神经网络(ANN)是由大量处理单元经广泛互连而组成的用来模仿人脑神经细胞结构和功能的系统，通过模拟脑神经元的学习功能，无需建立复杂的物理模型就能够映射任何复杂的非线性关系，可以很好地解决影响因素较多、规律不明显的非线性问题[3]。误差反向传播(BP)神经网络利用误差反向传播算法对网络进行训练，是目前应用最广泛的人工神经网络。

1 遗传算法优化BP神经网络原理及流程

BP神经网络具有较强的非线性映射能力、泛化能力、容错能力和联想记忆能力，适合处理一些内部机制复杂的非线性问题。学习过程包括工作信号的正向传播和误差信号的反向传播[4]。输入信号从输入层经隐含层，传向输出层，在输出端产生输出信号。

如果在输出层不能得到期望的输出，则转入误差信号反向传播。通过权值的不断修正使网络的实际输出更接近期望输出。

输出层的权值调整公式：

(1)

隐含层的权值调整公式：

(2)

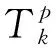
BP神经网络为局部搜索算法，存在收敛速率慢、易陷入局部极小值等缺陷[4-6]，利用遗传算法优化有利于提高收敛速度和预测精度[7-9]。

遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，具有良好的全局搜索能力，可以快速地将解空间中的全体解搜索出，不易陷入局部最优解的快速下降陷阱，在非规则的或有噪音的情况下，也能以很大的概率找到全局最优解，利用它的隐含并行性，可以方便地进行分布式计算，加快求解速度[10-11]。

其实现步骤如下。

1)编码，生成初始种群。遗传算法不能直接处理问题空间的参数，因此需要通过编码将其表示成遗传里的染色体结构。常用的编码方式有二进制编码、实数编码、符号编码等。本文采用实数编码方式对网络中每层的权值和阈值进行编码。对问题空间进行编码后会产生多个染色体，由这些染色体构成初始种群。

2)个体适应度评价。适应度函数用来表征种群中每个个体对其生存环境的适应能力，每个个体具有一个适应度。适应度是群体中个体生存机会的唯一确定性指标。本文采用BP神经网络训练样本的误差平方和E(i)的倒数作为个体适应度F(i)，即

(3)

式中：E(i)为个体i的误差平方和，F(i)为个体i的适应度。

3)选择。选择操作遵循优胜劣汰机制，从旧群体中以一定的概率选择优良个体组成的新种群，以繁殖得到下一代个体。适应度高的个体被遗传到下一代群体的几率大。选择操作有轮盘赌法、锦标赛法等多种方法，本文采用轮盘赌法，即基于适应度比例的选择策略[12]。个体i被选中的概率为

(4)

4)交叉。交叉就是互换随机2个染色体某些位上的基因，把父串的优秀特征遗传给子串，从而产生新的优秀个体。

5)变异。变异就是改变群体中随机选择的一个染色体某个(些)位上的基因，从而产生新的优秀个体。

利用遗传算法优化BP神经网络，使其既具有BP神经网络的鲁棒性和自学习能力，又具有遗传算法的全局搜索能力[13]。BP神经网络基于梯度下降方法进行权值的修正，结果随着赋予的初始权值变化而变化。在训练过程中，相关的网络参数完全凭借经验确定，易引起网络震荡，使收敛速度过慢。权值沿局部改善的方向逐渐进行调整，易收敛到局部极小点无法得到最优化的权值分布，降低网络的泛化能力。运用遗传算法的良好的全局寻优能力，进行全局搜索，获得最优权值和阈值，再导入BP神经网络进行精确求解，可以有效地缩短BP神经网络的收敛时间，提高预测结果的泛化精度。图1为遗传算法优化的BP神经网络流程图。本文遗传算法的基本参数为种群规模sizepop=30，遗传代数maxgen=50，交叉概率pcross=0.4，变异概率pmutation=0.1。

图1 遗传算法优化的BP神经网络流程图 Fig.1 Flow chart of BP neural network optimized by genetic algorithm

2 网络建立及数据处理

2.1 网络变量的选择

皮江法炼镁工艺是中国主要的制镁方法，是以硅铁为还原剂，在高温、真空条件下还原煅白中的氧化镁制取金属镁的工艺[14-15]，其工艺流程如图2所示。

图2 皮江法炼镁工艺流程Fig.2 Extraction process of magnesium by pidgeon

反应式为

2(MgO·CaO)+ Si = 2Mg+ 2CaO·SiO2。

镁还原率的计算公式：

(5)

式中：m为产镁量；a为球团质量；b为球团中煅白含量；c为煅白中MgO含量；q1为镁原子质量；q2为MgO分子质量。

真空热还原反应中镁还原率与工艺参数的关

系可以表示为

ηMg=f(Ac,tc,MSi,d,Pr,t,T,Pe，…)。

(6)

式中：Ac为煅白活性度；tc为煅白储存时间；MSi为配硅比；d为料粉粒度；Pr为制球压力；t为还原时间；T为还原温度；Pe为真空度。

本文选取煅白活性度、配硅比、制球压力、还原时间、还原温度和真空度等工艺参数作为输入变量，镁还原率作为输出变量。工业生产中各工艺参数的取值范围如表1所示。

表1 工艺参数取值范围Tab.1 Value ranges of process parameters

2.2 网络结构确定

BP神经网络拓扑结构通常包括输入层、一个或多个隐含层和输出层。隐含层的层数及其单元数的确定对整个网络模型的建立起着至关重要的作用。数学理论证明带有一个隐含层的BP神经网络可以以任意精度逼近任一连续函数。本研究选择含有一个隐含层的3层BP神经网络结构。隐含层单元数采用经验公式(7)确定[16]：

(7)

式中：p为隐含层单元数；n为输入层单元数；q为输出层单元数；a为1～10之间的整数。经过多次尝试，隐含层单元数选取为10，网络结构为6×10×1，如图3所示。

图3 三层BP神经网络结构图Fig.3 Three layer structure of BP neural network

2.3 样本数据收集及处理

样本数据来自某镁厂的生产数据。结合实际生产经验，对采集的数据进行筛选整理，剔除误差较大的数据，提取完整且具有一定分布的数据，尽可能全局反映各参数的变化规律。最后获得200组样本数据，随机采用其中150组用于网络训练，50组用于网络预测。

为平衡各训练参数，提高训练效率，需要对筛选后的数据进行归一化处理，使样本数据归一化到[0, 1]之间。归一化函数式[17]为

(8)

式中：y为归一化后的数据；x为归一化前的数据；xmax为归一化前数据的最大值；xmin为归一化前数据的最小值。

3 网络训练及结果分析

训练过程在MATLAB神经网络工具箱中进行，采用LM训练算法[18]，训练函数为trainlm，隐含层神经元的传递函数选用S型传递函数tansig，输出层神经元传递函数选择线性传递函数purelin。网络的学习因子Ir=0.1，训练次数为1 000，训练精度为0.000 1。

确定神经网络结构和参数后进行训练建立预报模型。为了确立模型的真实性和有效性，需用预测样本对网络进行测试和验证。图4 a)为标准BP神经网络预报模型镁还原率预测值和实际值对应情况，图4 b)为遗传算法优化的BP神经网络预报模型镁还原率预测值与实际值对应情况，图5为两种模型镁还原率预测值和实际值的误差曲线。误差分布见表2。

图4 镁还原率预测结果Fig.4 Prediction results of magnesium reduction degree

图5 镁还原率误差曲线Fig.5 Error curves of magnesium reduction degree

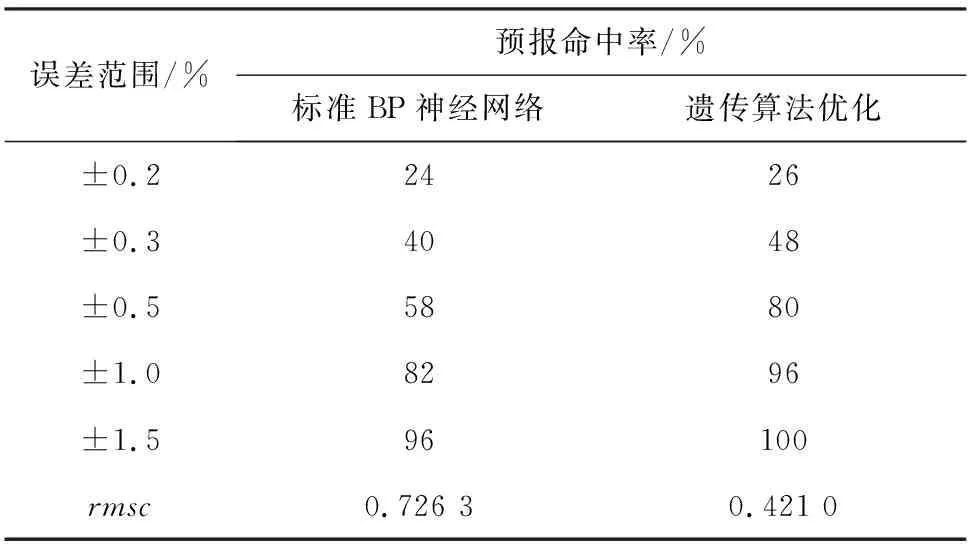
表2 镁还原率预测误差分布Tab.2 Error distribution of magnesium reduction degree

由表2可知，镁还原率预测值与实际值误差在±0.2%的范围内，标准BP神经网络预报命中率为24%，遗传算法优化的BP神经网络模型预报命中率为26%；误差在±0.5%的范围内，前者预报命中率为58%，后者为80%；误差在±1.0%的范围内，前者预报命中率为82%，后者达到96%。rmsc表示镁还原率预测值与实际值的均方根误差，遗传算法优化的BP神经网络预报模型的rmsc=0.421 0，与标准BP神经网络预报模型相比，具有更高的预测精度。

煅白活性度、配硅比、制球压力、还原温度、还原时间、真空度等是影响皮江法炼镁工艺镁还原率的重要因素，关系到吨镁能耗、污染物排放及生产成本。通过预报模型指导镁生产中工艺参数的组合问题，寻找最优的工艺参数组合，获得较高的镁还原率，有利于降低资源和能源消耗，降低生产成本，减少污染物排放，实现镁工业的节能与环保，提升镁工业的市场竞争力和环境相容性。

4 结 论

基于遗传算法优化的BP神经网络镁还原率预报模型能够较精确地预测皮江法炼镁工艺中的镁还原率，预报精度高，泛化能力强。镁还原率预测值与实际值误差在±0.2%的范围内，遗传算法优化的BP神经网络模型预报命中率为26%；误差在±0.5%的范围内，命中率为80%；误差在±1.0%的范围内，命中率达到96%，最大误差小于1.3%，均方根误差rmsc=0.421 0。

参考文献/References:

[1] MORDIKE B L, ENER T. Magnesium properties-application-potential[J]. Materials Science Engineering A, 2001, 302：37-45.

[2] 许并社, 李明照. 镁冶炼与镁合金熔炼工艺[M]. 北京：化学工业出版社,2006.

XU Bingshe,LI Mingzhao. Magnesium Smelting and Magnesium Alloys Melting Process[M]. Beijing: Chemical Industry Press, 2006.

[3] 华建社, 赵小龙, 刘明华. 基于BP神经网络的中厚板层流冷却终冷温度预报[J]. 南方金属， 2011(5)：8-11.

HUA Jianshe,ZHAO Xiaolong,LIU Minghua. Prediction of final cooling temperature of laminar cooling of plate based on BP neural networks[J]. Southern Metals, 2011(5)：8-11.

[4] 高 隽. 人工神经网络原理及仿真实例[M]. 北京：机械工业出版社,2008.

GAO Juan. Artificial Neural Network Principle and Simulation Examples[M]. Beijing： China Machine Press, 2008.

[5] SRINIVAS V, RAMANJANEYULU K. An integrated approach for optimum design of bridge decks using genetic algorithms and artificial neural networks[J]. Advances in Engineering Software, 2007,38(7)：475-487.

[6] 陈金辉,赵雷振,杨宗宵,等. 改进的BP神经网络在故障诊断中的应用[J]. 河北科技大学学报，2011,32(5)：455-459.

CHEN Jinhui, ZHAO Leizhen, YANG Zongxiao, et al. Application of improved BP neural network in fault diagnosis[J]. Journal of Hebei University of Science and Technology, 2011,32(5)：455-459.

[7] 苏力争,齐乐华,周计鹏,等. 基于GA-BP混合算法的液固挤压工艺组合参数逆向设计[J]. 塑性工程学报，2009,16(5)：5-9.

SU Lizheng, QI Lehua, ZHOU Jipeng, et al. Reversing design on combined parameters of liquid-solid extrusion process based on the predictive model using hybrid GA-BP algorithm[J]. Journal of Plasticity Engneering, 2009,16(5)：5-9.

[8] 李 松,罗 勇,张铭锐. 遗传算法优化BP神经网络的混沌时间序列预测[J]. 计算机工程与应用，2011,47(29)：52-55.

LI Song,LUO Yong, ZHANG Mingrui. Prediction method for chaotic time series of optimized BP neural network based on genetic algorithm[J]. Computer Engineering and Applications, 2011,47(29)：52-55.

[9] 王生全,刘柏根,张召召,等. 遗传算法的BP网络模型进行瓦斯涌出量预测[J]. 西安科技大学学报，2012,32(1)：51-56.

WANG Shengquan, LIU Baigen, ZHANG Zhaozhao, et al. Prediction of gas emission quantity of mining faces based on genetic BP neutral network optimal model[J]. Journal of Xi'an University of Science and Technology, 2012,32(1)：51-56.

[10] 韩锐锋. 遗传算法原理与应用实例[M]. 北京：兵器工业出版社，2010.

HAN Ruifeng. Genetic Algorithm Principle and Application Examples[M]. Beijing: Weapon Industry Press，2010.

[11] 肖庆玲,于军琪,王海峰. 基于遗传算法的蓄热式镁还原炉温度控制优化[J]. 西安建筑科技大学学报(自然科学版)，2012,44(4)：605-608.

XIAO Qingling, YU Junqi, WANG Haifeng. Optimization of temperature control of regenerative magnesium reducing furnace based on genetic algorithm[J]. Journal of Xi'an University of Architecture and Technology(Natural Science Edition), 2012,44(4)：605-608.

[12] 解丹蕊,薛惠锋,韩建新. 基于遗传算法的西安邮政配送路线优化研究[J]. 河北科技大学学报，2008,29(3)：214-218.

XIE Danrui, XUE Huifeng, HAN Jianxin. Study on optimization of Xi'an post logistics distribution routing by genetic algorithm[J]. Journal of Hebei University of Science and Technology，2008,29(3)：214-218.

[13] 赵子豪. 基于遗传算法-BP神经网络方法对疲劳短裂纹演化规律的分析[D].大连：大连理工大学，2011.

ZHAO Zihao. Analysis on the Law of Short Fatigue Crack Based on Genetic Algorithm and BP Neural Network[D]. Dalian：Dalian University of Technology,2011.

[14] 任 玲,夏德宏,任春晓. XR-Ⅱ新型蓄热式金属镁还原炉[J]. 有色金属工程，2012(2)：33-36.

REN Ling, XIA Dehong, REN Chunxiao. XR-Ⅱ new regenerative magnesium reduction furnace[J]. Nonferrous Metals Engineering, 2012(2)：33-36.

[15] 韩继龙,孙庆国. 金属镁生产工艺进展[J]. 盐湖研究，2008,16(4)：59-65.

HAN Jilong, SUN Qingguo. Progress of magnesium production process[J]. Journal of Salt Lake Research，2008,16(4)：59-65.

[16] 常运合,曾 智,张家泉,等. 基于BP神经网络的大方坯质量在线预报模型[J]. 钢铁，2011,46(5)：33-37.

CHANG Yunhe, ZENG Zhi, ZHANG Jiaquan, et al. Online quality prediction system of bloom castings based on BP neural network[J]. Iron and Steel, 2011,46(5)：33-37.

[17] 侯延辉,刘志义,柏 松,等．Al-Cu-Mg-Ag 合金时效强化的神经网络预测模型[J]． 材料热处理学报，2009,30(3)：203-208．

HOU Yanhui, LIU Zhiyi, BAI Song, et al．Prediction of aging strengthening of Al-Cu-Mg-Ag alloy based on neural network[J]．Transactions of Materials and Heat Treatment，2009，30(3)：203-208．

[18] HAGAN M T, MENHAJ M. Training feedforward networks with the Marquardt algorithm[J]. IEEE Transactions on Neural Networks, 1994, 5(6)：989-993.