弯曲海底峡谷中浊流的三维流动及沉积的初步研究①
2013-11-13张家年吴昊雨黄河清
黄 璐 张家年 吴昊雨 黄河清
(安徽工业大学环境流体研究所 安徽马鞍山 243002)
0 引言
浊流是在诸如地震、海底滑坡等触发机制下诱发的由水流湍流支撑的载有颗粒的、重力驱动的底流,是将大陆架上的碎屑沉积物迁移到深海的主要作用力之一[1,2]。海底浊流具有极大的破坏作用,可造成海底电缆的折断和一些海底设备及仪表的破坏[3]。浊流传播过程中会引发海底地形演变,形成沟渠、堤坝和海底扇沉积系统。同时海底浊流在运动过程中也会发生沉积,可能会形成含有油藏的浊积砂体[2,4]。近20年来,国内外和古代浊流沉积相关的深水油气探测已经取得了很大的进展,在南美、墨西哥湾、北海以及澳大利亚西北大陆架等海域的浊积岩中相继发现了许多大型海底油气田,勘探领域已扩展到以西非、巴西坎波斯盆地和墨西哥湾这3大热点地区为代表的水深3 000 m 以上的深海区[5,6]。
由于对浊流及其沉积的研究具有重要的经济、环境意义,国内外对其都十分重视。21世纪以来,浊流的三维研究逐渐增多。Peakall等[7]用一系列物理实验研究了具有恒定宽度的弯曲海底峡谷的沉积模式,发现在相同的地形条件下,海底弯曲峡谷中内岸的点坝反而比河流中的点坝所处的位置更远。Huang等[8]分析了横剖面为梯形的海底直峡谷中浊流的流动形态及沉积,通过数值模拟再现了海底浊流的自我建堤过程,并发现浊流沉积物平均粒径云图和沉积厚度云图在形状上相似,但在峡谷方向上略有延长。Amos等[9]通过在沉积物底床上释放盐水流的方式产生浊流,进行了不同弯曲度下的浊流流动实验,发现弯曲度足够大时,上游的溢流会重新进入下游的渠道中,产生异常的流动和沉积模式。Straub等[10]通过一系列实验,模拟了弯曲海底峡谷中浊流的流动和沉积,提出了一个控制浊流在峡谷内流动的速度最大值公式。尽管这一系列的实验研究对加深海底浊流的理解有帮助,但实验室实验由于规模和实验条件的限制,模型常常过于简化,一般模拟渠道的长度都不超过10 m;同时实验模拟耗资大,不易模拟大尺度的浊流。数值计算模拟海底浊流的三维流动形态及其沉积,有利于缩小模型与自然界真实浊流的差距,加深我们对自然界浊流的理解,同时具有相对于实验模拟的经济性和简便性。
本文采用一经多项实验数据验证的计算模型对深海中横剖面为圆弧形的弯曲海底峡谷中的浊流进行模拟并分析浊流在峡谷内部和漫滩上的流动、密度变化以及二次流和一些沉积特征。这些特征对于我们根据对浊流的沉积观察推测其形成环境及油气储层的调查等方面有一定的帮助作用。
1 模型概述
如图1所示,浊流流经的海底峡谷地形多为弯曲状,和地表的河流有许多相似之处(Wynne等,2007[11])。

图1 典型的海底峡谷示意图(据Wynn等,2007[11])Fig.1 Schematic diagram of typical submarine canyon(after Wynn,et al.,2007)
根据Straub等、Langbein和Leopold及Pirmez的对地表及水下渠道的观察及实验研究[10,12,13],本研究采用可以很好地模拟典型地面和水下渠道的理想正弦曲线[10,12,13]作为模型弯道的峡谷中心线,该曲线由两个波长为50 m的弯道组成,弯曲度为1.028,底坡坡度设置为0.001 5°。在弯道上游设有70 m的直道,以使浊流能以接近自然的状态进入弯道。两个弯道后的下游与100 m左右长的直道相连。计算模型与原型的长度比尺为1∶100,如图2所示,整个模型模拟的区域长约270 m,宽为170 m,峡谷的两边为漫滩;峡谷横剖面为曲率半径为10 m的圆弧,圆弧顶宽为10 m。计算模型可看作模拟一个在小坡度的弯曲峡谷内流动的海底浊流,计算区域沿x(流向)、y(垂向)、z(横向)方向的网格数分别为 100,40,120,共含4.8×105个计算网格点。
深海中浊流流速小到不足1 m/s,大到十几米/秒[1]。Prior等[14]对位于英国哥伦比亚的比特岛入口一个细长的渠道扇系统内长达1年的检测得出的数据表明,浊流最大速度为 3.35 m/s,Xu等[15]于2004年观测到浊流的速度最大值为1.9 m/s。从1929年纽芬兰大浅滩浊流事件对浊流的破坏估计的头部最大速度约为19 m/s[3],并且观察到的浊流中的颗粒物体积比浓度一般都较低,为0.1% ~7%[2]。在数值模拟计算中,应用密度弗雷德数相似准则,当长度比为1∶100时,设入口处的流速为0.26 m/s,入流含比重为2.65平均粒径为25 μm沉积物的体积比浓度为2%,相当于原型浊流的平均流速为2.6 m/s,在顶宽1 km,长约27 km弯曲峡谷内以同等的沉积物体积比流动,和上面提到的自然界中观察到的浊流速度接近。计算模拟的一些主要参数见表1。模拟浊流流动时间为600 s,入流面面积为6.40 m2,占峡谷横剖面面积的70.62%,位于峡谷横剖面的底部。
2 计算模型简述
含低密度沉积物的海底浊流可将其视为不可压缩的连续体,并应用鲍辛尼斯克假设(Boussinesq assumption)对其进行模拟[8]。在上述条件下模型的雷诺平均质量和动量方程如下:

图2 模型设置图(a).整个峡谷的俯视图及横剖面分布;(b).峡谷横剖面图;(c).峡谷处(b)图中的方框部分的放大图Fig.2 Schematic diagram of the model(a).Planform view of the canyon and the location of the cross-sections,(b).a transect of the canyon,(c).Close-up view of the rectangular part in(b)

表1 计算模拟主要参数Table 1 Main parameters of numerical simulation
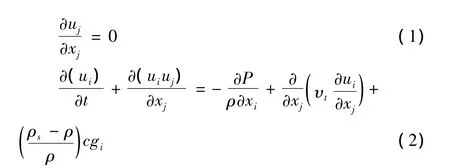
其中,ui,uj为 x1,xj方向上的雷诺平均速度,P为雷诺平均压力,ρ,ρs分别为环境流体和沉积物密度,c为悬浮沉积物的雷诺平均体积比浓度,gi为重力加速度。υi为涡黏度系数,通过求解经浮力项修正的如下湍流k-ε模型,得

式中k为湍流动能,ε为湍流动能耗散率。沉积物质量守恒方程为

式中,υs为沉积物颗粒的下降速度,δj2为克罗内克符,Sct为施密特系数。在模型中假设悬浮沉积物随流体一同流动,但在垂直方向有一下降速度,此速度根据由实验确定的经验方程来计算。
假定到达航道入口的船舶数量为一个计数过程,每艘船舶到达时间是相互独立的,而且在充分短的时间区间上最多只到达一艘船舶。在数学上,这一过程一般采用泊松分布来描述,其中单位时间到达的船舶数量用参数λ表示。
本模型计算模拟海底浊流的几乎所有重要的物理过程,在河床的底部边界采用Exner方程模拟由于沉积物的沉积、夹带和推移质搬运导致的底床平面的改变[16]。沉积物沉积速度根据由方程(4)计算的河床底部沉积物体积比浓度与沉积物沉降速度相乘得出,沉积物夹带速度和推移质搬运分别根据Smith和Mclean[17]以及 van Rijn[18]实验得出的经验公式计算,详细请参见所给出的参考文献。
应用了基于非正交网格的有限体积法来对上述模型方程进行数值求解,具体解法请参见参考文献8及16。此模型经实验的连续入流的水下盐水密度流、含单粒径及多粒径浊流、突然释放型的重力流以及三维直渠道内的浊流流动及沉积验证,均取得了理想的模拟结果[8,16,19,20]。
3 模拟结果及讨论
应用上述数值计算模型模拟了参数如表1所示的浊流在如图2所示水下弯曲渠道内的流动,观察到的浊流在海底峡谷水平面上的密度分布、峡谷横剖面的直道及弯道顶点中心沿流向速度分布、直道及弯道顶点处的密度分布、弯道顶点处的二次流特征等如下。
3.1 海底峡谷水平面上的浊流密度分布
浊流的驱动力来自于与环境流体的密度差,浊流在流动过程中会逐渐形成密度分层,还会伴随着颗粒沉积及夹带,形成一些类似于河流点坝的沉积形态。图3显示了峡谷顶部上方0.005 m处的密度分布云图,从图中可以看出:
(1)在弯道前的直道尾部,流体已经有明显的外溢,因为浊流在运动过程中不断夹带上层周围流体,使浊流厚度不断增加,当浊流厚度超过峡谷深度时就会外溢,到达漫滩区域,其中的悬浮沉积物将在漫滩上沉积;
(2)在弯道顶点外岸处,浊流发生了明显的流动剥离(Kassem和Irman[21]将流体由于离心力导致的在弯道处溢出峡谷外称为“剥离(stripping)”,将峡谷任意处由于与周围流体的夹带带来的流体厚度的增加所导致的流体溢出峡谷外称为“溢流(spilling)”,在这里我们也采用此种说法),使浊流产生大量的动量和密度损失,从而使峡谷内的沉积型浊流的速度和密度减小;
(3)弯道外岸和内岸产生了明显的密度差,弯道内岸基本保持了与环境流体相近的密度,而在弯道外岸,浊流密度明显增大。每个弯道顶点处,漫滩区域的流体密度在靠近弯道外岸处达到最大,其中无量纲过量密度最大可达入流的37.5%,然后随着与外岸距离的增加而减小;
(4)随着沿流向距离的增加,浊流剥离产生的密度损失越来越小,由区域B至E,最大无量纲过量密度从入流的37.5%逐渐减小为18.8%。区域A的特殊性是因为刚进入弯道时流体所受的离心力较小,导致剥离较少。
这些模拟结果和美国的Straub等[10]以及英国的Kane等[22]的实验观察基本是一致的。
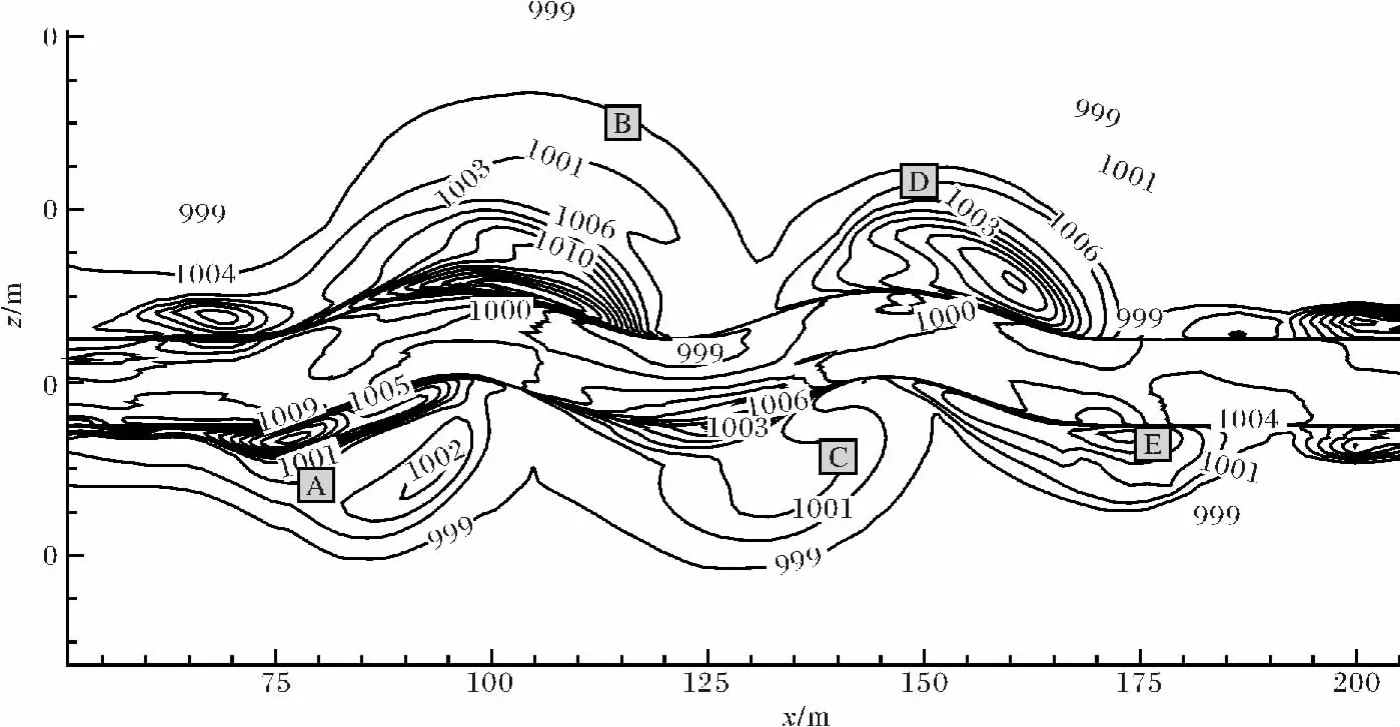
图3 峡谷顶部上方0.005 m处的密度(kg/m3)云图Fig.3 Density(kg/m3)contour of the current at 0.005 m above the canyon top
3.2 峡谷横剖面直道及弯道顶点中心沿流向速度分布
图4显示了峡谷直道末端x=70 m处和三个弯道顶点,即x=95,120,145 m处的横剖面中心线的纵向速度结构(对应图2a横剖面2~5),横坐标表示浊流水平速度,纵坐标表示距峡谷底部的高度。直道上浊流的纵向速度结构与实验室测得的直渠道内浊流基本一致,即在距底部不远处,存在一速度极大值,其下为壁面边界层流,其上为自由剪切层流[23]。但在三个弯道顶点处,最大速度上方部分,速度结构曲线平滑,最大值下方,流向速度曲线出现一明显的可能是由于二次流引起的波动,与Kane等[22]的实验观测值一致;并且有越往下游的弯道顶点处沿流向最大速度越小,其下波动位置越往上移的特征,反映了沉积型浊流渐渐减弱的特性。第一个弯道顶点处中心线的最大流速较前面直道上的要大,是因为浊流的运动受到离心力影响,流体整体朝外岸倾斜,外弯部分的流体速度密度都比内弯大,因此峡谷中心线的速度相对于直道上有所增大。
3.3 弯道顶点处的浊流密度分布
浊流与环境流体的密度差相对较小,所以在弯道处浊流在外岸处的升高会比明渠流中的水要高得多。Keevil等[24]于2006年用实验说明了控制海底和河流峡谷的演化和迁移的流动过程可能存在极大的差异,并指出海底峡谷的形成和演化也可能显示出与具有相似地形的河流峡谷不同的特征。图5a~d所示的图2中1,3,4,5横剖面的密度云图(图中I表示内弯,O表示外弯)有如下特征:

图4 三个弯道转换处的横剖面中心线处的纵向速度结构Fig.4 Longitudinal velocity profile at the canyon centerline of each apex of the three bends
(1)直道内的浊流基本上是对称的(图5a);
(2)浊流在弯道处峡谷上部显示出向着外岸倾斜的特征,在和岸高相同的水平高度处弯道外弯的密度明显比内弯的大(图5b,c,d),这与图3所显示的密度分布特征是一致的;
(3)在峡谷的底部,浊流密度显示了与上部不同的分布特征,靠近弯道内弯处底部的密度要高一些(图5b,d),这是由于受到下节所分析的弯道中的二次流影响的原因;
(4)流体自上而下出现密度分层,密度层具有越往底部密度增加越快的特征,这是由于受到颗粒沉积的影响。密度层上层等高线厚度逐渐增加,这是因为浊流在运动过程中不断夹带周围流体,与周围流体进行交换,使本身密度减小。
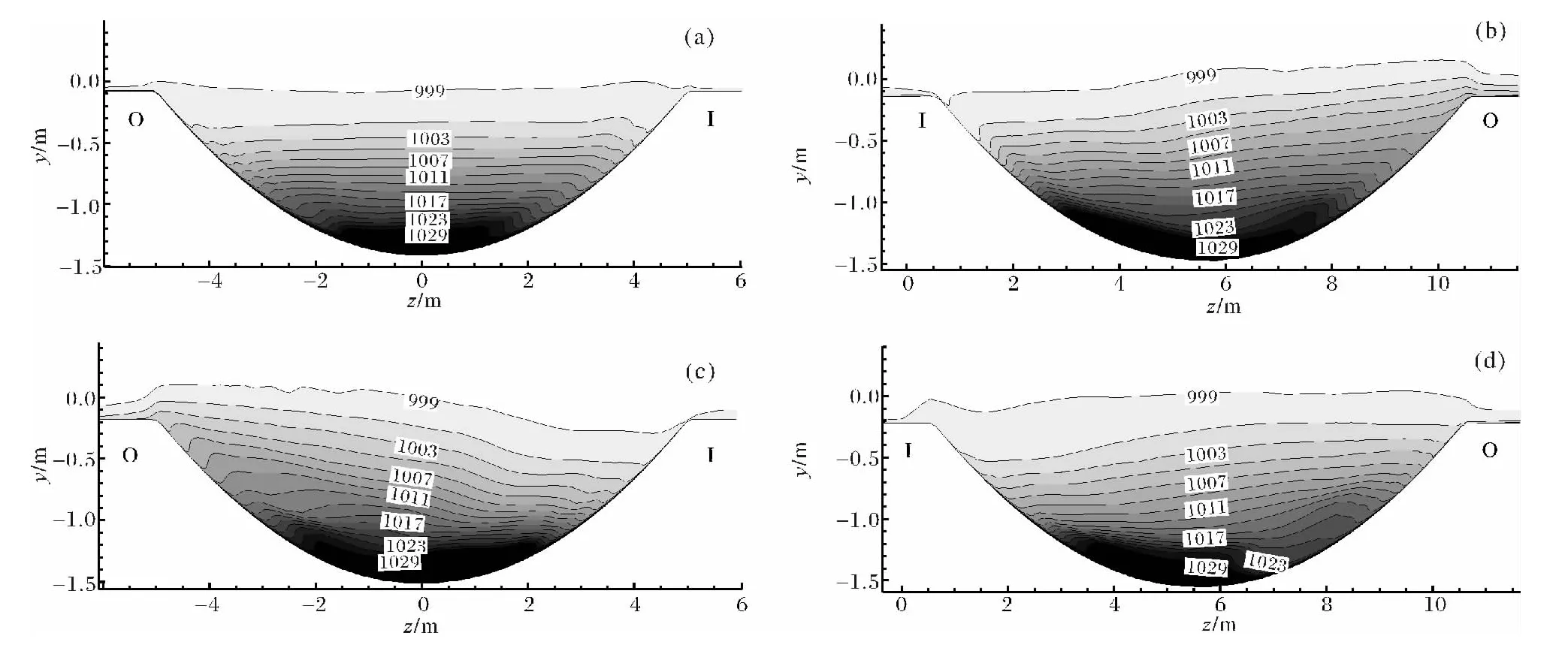
图5 直道1(a)及弯道横剖面3-5(b,c,d)的密度(kg/m3)云图Fig.5 Density(kg/m3)contours of cross-section 1(a)and cross-sections 3 to 5(b,c,d)
3.4 弯道顶点处的二次流特征
浊流在弯曲峡谷中的二次流非常明显,最近有一系列关于水下重力流在弯曲峡谷内的二次流的实验、计算模拟及理论分析论文,讨论弯道顶点处的浊流流动方向究竟和河流一样还是相反[25~28],Abad 等[27]根据实验和理论分析得出弯曲矩形渠道内的盐水重力流二次流的方向会因为流态的不同而不同,Serchi等[28]则指出二次流的方向会因为坡度的变化发生改变。图6a和图6b表示第一个弯道顶点(x=95 m)处峡谷横剖面以及弯道外岸峡谷和漫滩交界处的速度矢量图(I表示内岸,O表示外岸),由图中可见:
(1)对于我们所模拟的小坡度、低弯曲度的圆弧形峡谷来说,弯道顶点底部的二次流是和河流类似的顺时针方向的(图6a),而在 Serchi等[28]的模拟结果中也曾提到在低坡度下,弯曲渠道中的二次流方向是与河流中的一致的,Kassem和Irman[21]所模拟的小坡度矩形水下弯曲渠道中的二次流方向也是如此,和我们的模拟结果相符合;Corney等[25,26]论及的水下浊流在弯道顶点处是二次流和河流相反的观点可能并不具一般性;
(2)图6b显示:弯道外岸,浊流在峡谷与漫滩交界处发生分流,一部分沿着峡谷边壁向下流动,另一部分则流向漫滩;
(3)正是由于底部二次流动的方向指向内岸,从而在弯道顶点处使底部高密度浊流向内弯倾斜,和顶部浊流的向外岸倾斜不同(参见图5b,d)。
图6 第一个弯道顶点(x=95 m)横剖面(a)及其外岸局部(b)的速度矢量图Fig.6 Velocity vector of the first bend apex cross-section(a)and a close-up of its outer bank region(b)
总的说来,根据我们模拟的结果及综合其它的实验和模拟结果[25~28]来看,海底浊流在弯曲峡谷内的二次流的方向及形态不仅和流态而且和峡谷的形状及宽深比等都有一定的关系,不可一概而论。
3.5 基本沉积特征
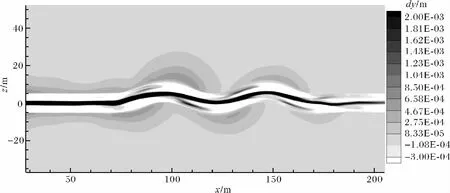
图7 t=600 s时的底床上颗粒物沉积厚度Fig.7 Sedimentary thickness over the bed at t=600 s
浊流中的悬浮沉积物在运动迁移过程中会发生沉积,同时快速流动的浊流会侵蚀底床,重塑底床形态。图7显示了所模拟浊流在t=600 s时的沉积厚度分布。峡谷底部中心线附近两边有较多的沉积,由于边壁较陡,峡谷边壁上则出现小规模的侵蚀,这将造成峡谷横剖面形状的轻微改变;进入弯道前,直道上的沉积厚度分布基本是对称的;峡谷外漫滩部分由于浊流有外溢,也产生了少量的沉积,并随着与峡谷中心线距离的增加而递减;进入弯道后,在弯道内部,每个弯道顶点外岸上游,即内岸下游处有明显的由于迴流导致的沉积,而在外岸下游处则发生侵蚀,与A-mos等[9]实验观测到的一致,长期的内岸下游沉积和外岸下游侵蚀会造成峡谷整体形状的变化,即弯曲度和峡谷宽度的变化,以及峡谷轴线的迁移。在峡谷弯道顶点的外岸漫滩及其下游方向上,由于离心力的作用产生较多的沉积,并呈由上游向下游逐渐递减的趋势。本研究给出了海底弯曲峡谷中一次浊流事件的基本沉积特征,可见其趋势与实验观察及海底实测的一些研究相符合[9~11],今后我们将进一步研究多次浊流事件所形成的沉积序列。
4 总结
本研究对圆弧形弯曲海底峡谷中的浊流的流动及其沉积进行了三维数值计算模拟和分析,得到如下主要结论:浊流在运动过程中不断夹带周围流体使浊流厚度增加,随着浊流厚度超过峡谷深度,产生溢出;浊流到达弯道部后,由于离心力的作用会产生更多的溢出,其最大过量密度可达入流的37.5%;弯道顶点横剖面处的二次流在峡谷底部形成了一个类似于河流二次流的循环,靠近底床处的方向从外岸指向内岸;弯道外弯处岸边观察到分流。观察到的浊流在水下弯曲峡谷的沉积特征为:每个弯道顶点内岸下游处有由于回流产生的沉积,而在外岸下游处则发生侵蚀,在峡谷弯道顶点的外岸漫滩及其下游方向上,由于离心力的作用产生较多的沉积,并呈现由上游向下游逐渐递减的趋势。本研究的模拟结果不仅确认了一些已知的实验事实,并且提供了浊流在海底峡谷内流动及沉积相关联的一些新的信息,有助于进一步加深对浊流运动和沉积关系的理解和认识。
References)
1 Middleton G V.Sediment deposition from turbidity currents[J].Annual Review of Earth and Planetary Sciences,1993,21:89-114
2 Meiberg E,Kneller B.Turbidity currents and their deposits[J].Annual Review of Fluid Mechanisms,2010,42:135-156
3 Heezen C B,Ewing M.Turbidity currents and submarine slumps,and the 1929 Grand Banks earthquake[J].American Journal of Science,1952,250:849-873
4 姜辉.浊流沉积的动力学机制与响应[J].石油与天然气地质,2010,31(4):428-435[Jiang Hui.Dynamical mechanism and depositional responses of turbidity current sedimentation[J].Oil& Gas Geology,2010,31(4):428-435]
5 杨川恒,杜栩,潘和顺,等.国外深水领域油气勘探新进展及我国南海北部陆坡深水区油气勘探潜力[J].地学前缘,2000,7(3):247-256[Yang Chuanheng,Du Xu,Pan Heshun,et al.Advances in worldwide deep water hydrocarbon exploration and oil and gas exploration potential in the northen continental slope in South China Sea[J].Earth Science Frontiers,2000,7(3):247-256]
6 何家雄,夏斌,施小斌,等.世界深水油气勘探进展与南海深水油气勘探前景[J].天然气地球科学,2006,17(6):747-752[He Jiaxiong,Xia Bin,Shi Xiaobin,et al.Prospect and progress for oil and gas in deep waters of the world,and the potential and prospect foreground for oil and gas in deep waters of the South China Sea[J].Natural Gas Geoscience,2006,17(6):747-752]
7 Peakall J,Amos K J,Keevil G M,et al.Flow processes and sedimentation in submarine channel bends[J].Marine and Petroleum Geology,2007,24:470-486
8 Huang H Q,Imran J,Pirmez C.Numerical model of turbidity currents with a deforming bottom boundary[J].Journal of Hydraulic Engineer-ing,2005,131(4):283-293
9 Amos K J,Peakall J,Bradbury P W,et al.The influence of bend amplitude and planform morphology on flow and sedimentation in submarine channels[J].Marine and Petroleum Geology,2010,27:1431-1447
10 Straub K M,Mohrig D,Buttles J,et al.Quantifying the influence of Channel sinuosity on the depositional mechanics of channelized turbidity currents:A laboratory study[J].Marine and Petroleum Geology,2011,28:744-760
11 Wynn R B,Cronin B T,Peakall J.Sinuous deep-water channels:Genesis,geometry and architecture[J].Marine and Petroleum Geology,2007,24:341-387
12 Leopold L B,Langbein W B.River meanders[J].Geological Society of America Bulletin,1966,71:769-793
13 Pirmez C.Growth of a submarine meandering channel-Levee system on the Amazon Fan[D].New York:Columbia University,1994
14 Prior D B,Bornhold B D,Wiseman W J,et al.Turbidity current activity in a British Columbia Fjord[J].Science,1987,237:1330-1333
15 XU J P,Noble A M,Rosenfeld K L.In-situ measurements of velocity structure within turbidity currents[J].Geophysical Research Letters,2004,31:1-4
16 Huang H Q,Imran J,Pirmez C.Numerical modeling of poorly sorted depositional turbidity currents[J].Journal of Geophysical Research,2007,112:1-15
17 Smith J D,McLean S R.Spatially averaged flow over a wavy surface[J].Journal of Geophysical Research,1977,82(12):1735-1746
18 Rijn,L C van.Sediment transport,part II:suspended load transport[J].Journal of Hydraulic Engineering,1984,110(11):1613-1641
19 Huang H Q,Imran J,Pirmez C.Numerical study of turbidity currents with sudden-release and sustained-inflow mechanisms[J].Journal of Hydraulic Engineering,2008,134(9):1199-1209
20 Huang H Q,Imran J,Pirmez C.The depositional characteristics of turbidity currents in submarine sinuous channels[J/OL].Marine Geology,2012,329-331:93-102
21 Kassem A,Irman J.Three-dimensional modeling of density current.II.Flow in sinuous confined and unconfined channels[J].Journal of Hydraulic Research,2004,42(6):591-602
22 Kane A I,McCaffrey W D,Peakall J,et al.Submarine channel levee shape and sediment waves from physical experiments[J].Sedimentary Geology,2010,223:75-85
23 Garcia M H.Depositional turbidity currents laden with poorly sorted sediment[J].Journal of Hydraulic Engineering,1994,120(11):1240-1263
24 Keevil G M,Peakall J,Best J L,et al.Flow structure in sinuous submarine channels:velocity and turbulence structure of an experimental submarine channel turbulence structure of an experimental submarine channel[J].Marine Geology,2006,229:241-257
25 Corney K P,Peakall J,Parsons D R,et al.Reply to discussion of Imran et al.on"the orientation of helical flow in curved channels"by Corney et al.,Sedimentology,53,249-257[J].Sedimentology,2008,55:241-247
26 Corney K P,Peakall J,Parsons D R,et al.The orientation of helical flow in curved channels[J].Sedimentology,2006,53:249-257
27 Abad J D,Sequeiros O E,Spinewine B,et al.Secondary current of saline underflow in a highly meandering channel:experiments and theory[J].Journal of Sedimentary Research,2011,81:787-813
28 Serchi G F,Peakall J,Ingham B D,et al.A unifying computational fluid dynamics investigation on the rive-like secondary circulation in submarine channel bends[J].Journal of Geophysical Research,2011,116:1-19
