井下核磁共振测井仪微弱信号处理算法设计

宋公仆 张嘉伟 薛志波 王光伟

（中海油田服务股份有限公司油技事业部 油田技术研究院，中国 北京 101149）

0 引言

核磁共振测井方法可直接测量地层孔隙中可动流体的信息，可定量确定自由流体、束缚水、渗透率及孔径分布，其孔隙测量不受岩石骨架矿物成分的影响，因此目前颇受测井行业的广泛应用[1]。与此同时，通过核磁共振测井采集到的地层回波信号相当微弱，其幅度值大概在40nV～2uV之间，几乎不可能通过常规测试手段直接检测到相应信号。本文重点介绍了两种微弱信号的提取算法，通过这两种算法可以有效地从采集到的微弱回波信号中快速提取相关信号幅度与相位信息，因此目前普遍应用于核磁共振微弱信号的提取处理上。

1 微弱信号处理算法分析

1.1 相敏检波算法（DPSD）分析

目前，对于纳伏级（nV）微弱信号电压的测量仪器主要有锁定放大器和取样积分器两类。前者是物质表面组份分析和表面电子能态研究的重要手段；后者使得核磁共振技术得以真正实现。这两类微弱信号检测仪器可测量到淹没在强噪声中的μV～nV量级的电压信号[2]。不过由于测量系统以及各种外界干扰引入的各种噪声使得噪声强度高出有用信号几十倍，一些常规的电压测量方法无法测量淹没在强噪声中的电压信号。对于这些信噪比低至-30～-60db范围的混于噪声中的微弱信号的测量均采用基于最大似然估计的互相关方法[3]。下面重点对互相关法的一种DPSD相敏检波算法进行详细介绍。

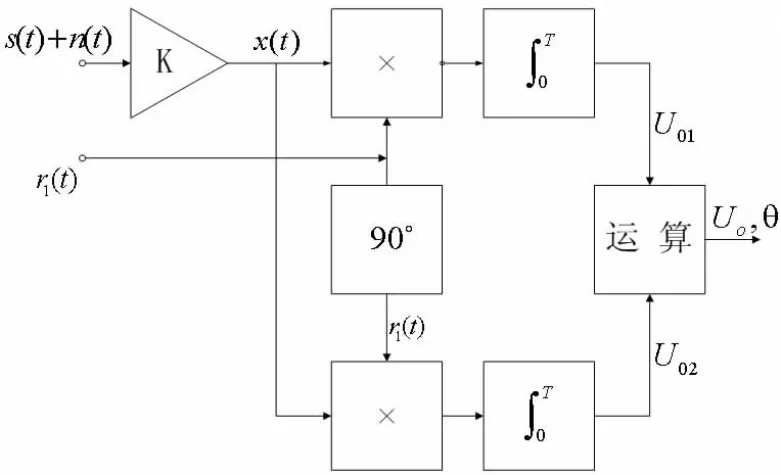
图1 双通道互相关器检测方法-DPSD算法结构图

图1中清晰列出了相敏检波算法的结构图，其中设被测信号x（t）为：

式（1）中 K 为测量电路放大器增益，n（t）为零均值高斯噪声。图1中对应的输出值为对正弦信号x（t）的幅值Us以及相位θ的最大似然估计。其中

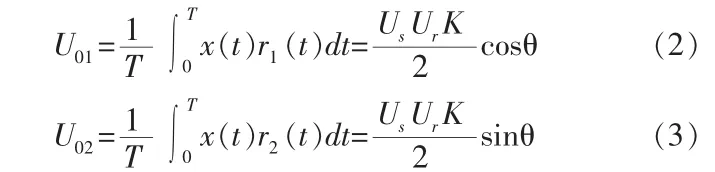
式（2）、（3）中参考信号 r1（t）及 r2（t）为相互正交且与 x（t）同频的正弦信号。 r1（t）=Urcosωt，r2（t）=Ursinωt。

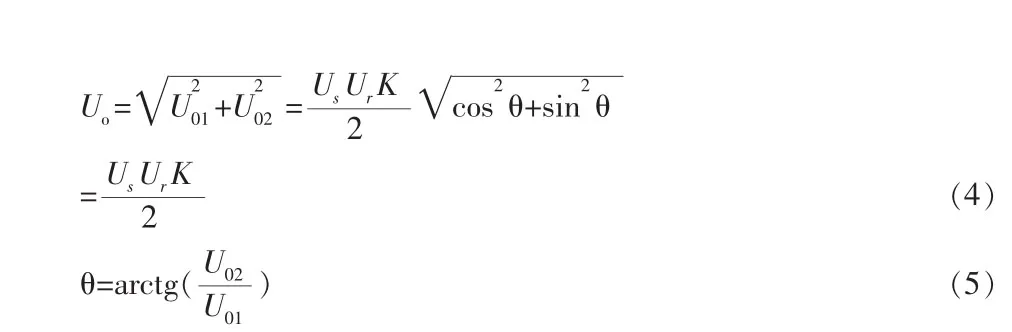
已经证明，由最大似然估计得到的正弦信号幅度及相位属于一致、有效估计。但是当被测正弦信号为纳伏量级时，测量系统噪声是信噪比低至-30db～-60db，则在有限测量时间T以内，U01和U02的测量结果会有较大的起伏波动，从而严重妨碍了正弦参量Us以及θ的精确测量。显然，如何选择合适的测量电路以及参数是微弱正弦信号检测的关键技术[4]。

而DPSD算法（数字相敏检波算法）是指利用计算机或DSP芯片实现式（2）以及（3）的相敏解调算法。将以上二式数字化后，可写成

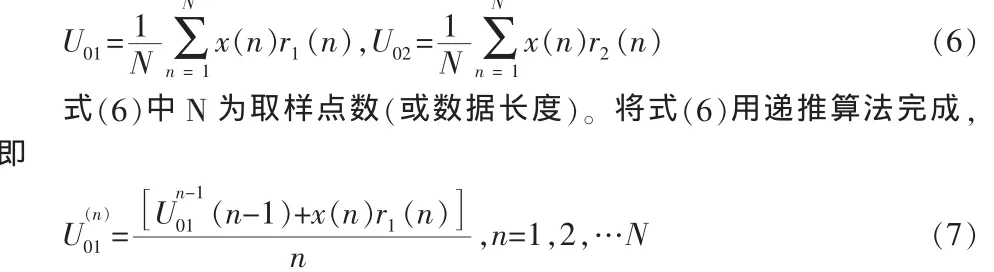
式中的 U01（n）为第 n 次取样后的计算平均值。 r2（n）与 r1（n）相位差90°（如图 1），故r2（n）可以通过 r1（n）来产生，但由于 r1（n）是取样信号，故要求r1（n）一周期内的取样点数与原频率之比为4的整倍数，即m为4的整倍数。fs为采样频率（r（n）采样频率必须等于x（n）采样频率）。在预先存储中可以先让Ur为1，最后通过计算得出的相位是采样起始点处的初相[5-6]。最后利用式（4）和（5）求出回波的幅值和相位。

以下是参考信号 r1（n）与 r2（n）和 U（n）02的相关计算公式。

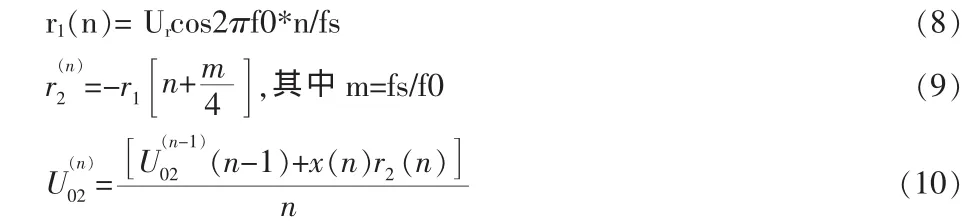
为了验证以上算法我们输入标准正弦信号并加入噪声后如下图2左边所示，可以看出信号淹没在噪声中，利用DPSD算法进行提取后其提取结果如图2右边所示：

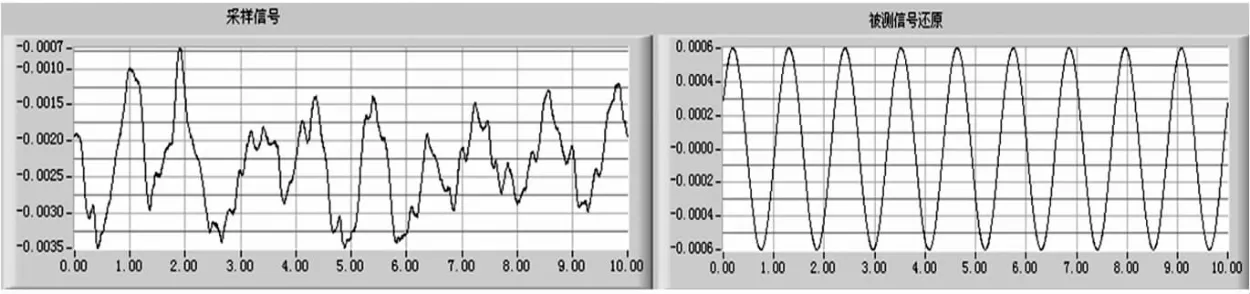
图2 DPSD算法提取信号试验测试结果

从上图2中，我们可以清晰地看到原始输入信号混入白噪声后形状已经失真，无法直观辨别输入信号的实际形状。将混入噪声的输入信号进行上述DPSD相敏检波算法处理后得到图2右边所示的原始信号波形。从图中我们可以直观看到通过DPSD算法处理后，利用该算法选频特性好的特点成功地将信号从噪声中提取出来。

1.2 小波提取算法设计

小波变换在当前微弱信号处理中应用越来越多，它是时间（空间）频率的局部化分析，通过伸缩平移运算对信号（函数）逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了Fourier变换的困难问题，成为继Fourier变换以来在科学方法上的重大突破[3]。有人把小波变换称为“数学显微镜”。

1.2.1 含噪信号的小波域表述

假定待提取的信号是一个有用信号与噪声的叠加效果，通过一种正交小波变换，可以最大程度的消除了信号的相关性，将能量集中到少数的小波系数上，从而达到滤除噪声的目的。首先来分析其中噪声小波域的分布规律。平稳白噪声的正交小波变换仍然是平稳的白噪声，其小波系数仍是互不相关的，分布在各个尺度下的所有时间轴上。假设 n（t）是一个方差为 σ2的宽平稳白噪声，ψ（t）是一个小波函数，则白噪声n（t）的小波变换的期望值为：

上式（11）中Ws为小波变换系数因子。上式（11）表明，随小波变换尺度S的增加，白噪声的小波变换幅值的均值E{|Wsn（t）|2}在减少，其衰减正比于1/S。若白噪声n（t）是高斯白噪声，在变换尺度S上，其小波变换模的平均密度为：

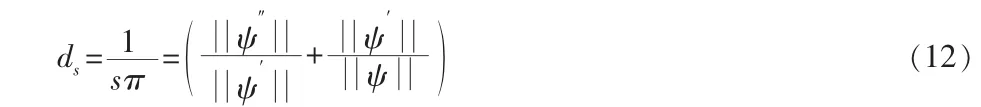
上式（12）说明，高斯白噪声的小波变换模值的平均密度正比于1/S，随着分解尺度S的增大，其密度减小。由上述两式性质可知，随着分解尺度S的增加，噪声的小波谱因幅度和密度的逐渐减少而将逐渐消失，从而达到滤出噪声的目的。下面来分析信号的小波域表述。设信号f（t）是光滑且P次连续可微的函数，ψ（t）是具有p阶消失矩的实正交小波，其支撑为[c，d]，有下式（13）所示关系：

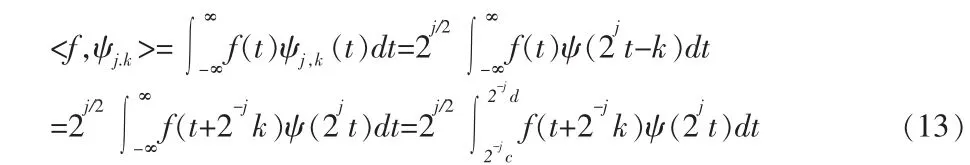
若上式（13）中 j足够大，ψjk（t）变得足够窄，将 f（t+2-jk）用其在 2-jk处的p阶泰勒级数展开近似表示，即：

1.2.2 提升小波算法

小波分析在实际工程中的应用主要通过以下三种方式：MALLAT算法、多孔算法以及提升算法[5]。前两种算法均建立在经典小波分析基础之上，其核心是基于二进平移和伸缩思想的小波变换和多分辨率分析，而经典小波分析则由傅里叶变换发展而来，因此MALLAT算法和多孔算法或多或少都会受傅里叶变换的影响。而提升小波算法相比基于经典多分辨率分析的小波（第一代小波）最主要优点是：改进了第一代小波算法，使其更易于实现。提升算法不存在卷积运算，节省了大量的计算时间和程序空间，计算量只有MALLAT算法的一半且避免了卷积计算存在的边界问题；计算过程简单明确，易于实现，可以采用原位计算，只需申请少量的额外存储单元，节省了存储空间；摆脱了傅里叶变换的束缚，可在第一代小波基的基础上较为方便的设计满足需要的小波基，尽管不能发现新的小波基，但可以改善现有小波基的特性，如消失矩特性等。小波滤波器组中滤波器h可以表示为式（16）所示的多相位形式，式中 he（z）和 ho（z）如式（17）所示，分别包含了 h（z）的偶系数和奇系数[7]。

上式（18）中称P（z）为多相位矩阵。小波分解重构的多相位表示如图3所示。

图3 小波分解重构的多相位表示

Daubechies和Swedens在此基础上提出了多相位矩阵因子分解的定理：若 P（z）的行列式等于 1，则总存在 Laurent多项式 ui（z）和 pi（z）以及非零常数 K，使得

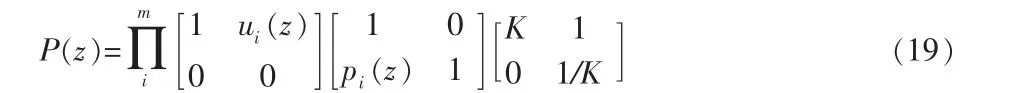
上式（19）中pm（z）=0。根据多相位矩阵的因式分解以及图4所示小波分解重构的多相位表示，得到下式（20）和式（21）：

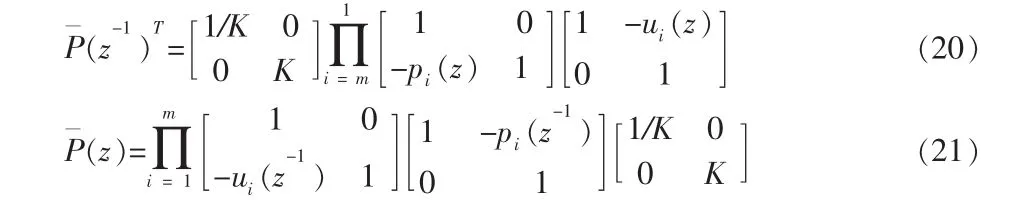
进一步得到如图4所示的小波分解过程的提升算法流程图以及图5所示的小波重构过程的提升算法流程图如下：

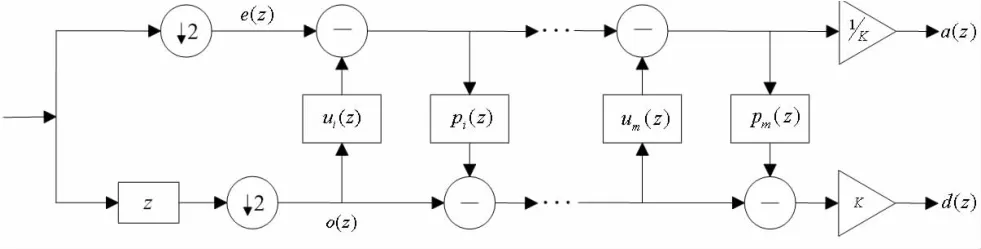
图4 小波分解过程的提升算法流程图

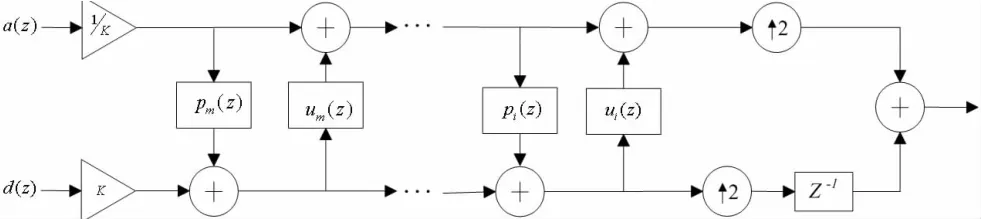
图5 小波重构过程的提升算法流程图

上图4所示为一层提升小波分解流程图，得到近似系数a（z）与细节系数d（z），在反复按照图4所示进行多层提升小波分解最终得到最底层的近似系数与细节系数。图5为一层小波重构过程的提升算法流程图，它是提升小波分解的逆运算，通过反复执行提升小波重构过程从而使分解的小波信号重构成去噪后的有用信号。

2 结束语

本文论述了在核磁共振测井中微弱信号提取的两种实现算法（DPSD）相敏检波算法与小波提取算法，对这两种算法进行了详细的介绍与分析。在核磁共振测井中，很多都利用这两种提取算法对采集到的回波串信号进行信号提取处理，其有着很好的噪声抑制和信号提取的能力[8]。这两种微弱信号提取算法已经成功应用在实际核磁共振测井仪器上，并取得了很好的应用效果。

［1］George Coates，肖立志，Manfred Prammer.核磁共振测井原理与应用[M].孟繁莹，译.北京：石油工业出版社，2007.

［2］邵维志，庄升，丁娱娇.一种新型核磁共振测井仪：MREx[J].石油仪器，2004.

［3］Pollak V L and Slater R R.Input Circuit for PulsedNMR[J].The Review of Scientif ic Instruments，1966.

［4］华中科技大学.微弱信号检测技术资料[Z].

［5］戴逸松.微弱信号检测方法及仪器[M].北京：国防工业出版社，1994.

［6］张新发，刘富，戴逸松.DPSD算法性能研究及参数选择[J].吉林工业大学学报，1998，3（28）：40-45.

［7］戴逸松.测量低信噪比电压的数字相敏解调算法及性能分析[J].计量学报，1997，18（2）：126-132.

［8］肖立志.核磁共振成像测井与岩石核磁共振及其应用[M].北京：科学出版社，1998.