分数阶微分算子增强图像边缘和纹理
2013-11-12周昌雄陶文林颜廷秦马国军
周昌雄,陶文林,尚 丽,颜廷秦,2,马国军
(1.苏州市职业大学电子信息工程系,江苏苏州215104;2.苏州市数字化设计与制造技术重点实验室,江苏苏州215104;3.江苏科技大学电子信息学院,江苏镇江212003)
1 引言
图像是记录和传递信息的重要载体和手段,由于多种原因,图像在生成、传输和变换的过程中会产生质量下降和特征淹没现象,对图像分析和识别带来困难[1-3]。因此,突出图像中的有用信息,扩大图像中不同物体特征之间的差别,从而改善图像的视觉效果是图像增强的目的。目前,人们提出了很多图像增强的算法,如基于直方图的增强和基于空域或频域的增强等。采用基于空域的传统整数阶微分方法增强图像的纹理信息,其微分结果约等于零,必然会使纹理细节大幅衰减,造成图像的纹理细节和边缘模糊不清[4-6]。因此,既要提升图像边缘又要加强纹理细节,成为图像增强研究的热点和难点问题。
分数阶微分是整数阶微分运算的推广,通过对分数阶微分的理论研究发现,在对信号进行分数阶微分运算,当微分阶次小于1时,既能大幅提升信号的高频分量有能加强信号中的低频分量,且对信号的甚低频没有进行大幅衰减。相较传统的整数阶微分图像增强方法,分数阶微分用于图像增强处理将使图像边缘明显增强、图像纹理细节更加清晰并且非线性保留图像平滑区域信息[7-8]。在文献[4]中运用5×5窗口大小,对灰度图像和彩色图像采用不同分数阶微分算子增强,实验结果表明,当微分阶次在0.4~0.6之间图像的增强效果最好,图像的边缘信息和局部纹理细节被加强,当微分阶次大于0.6以后图像中的噪声明显被放大。在文献[9]中,将5×5窗口分数阶微分模板分解为八个不同方向的小模板,求得像素点周围八个方向加权和的最大值作为该像素点的增强值。实验表明,改进方法既增强图像边缘又丰富了图像的纹理细节信息。图像像素邻域内像素点的灰度值具有关联性,分数阶微分算子模板窗口越小,模板窗口内像素点的灰度值关联性越大。本文提出将3×3模板窗口划分成四个方向的小模板,求得中心像素点周围四个方向加权和的最大值作为该中心像素点的增强值,据此增强图像的边缘信息和纹理细节信息能获得较明显效果。
2 分数阶微分原理
2.1 分数阶微分频域性质
对于任意平方可积的能量信号s(t)∈L2(R),设其Fourier变换为S(ω),则ν阶分数微分Dνs(t)的Fourier变换如下:

信号ν阶分数微分Dν算子其特性函数为:

其中,α(ω)和θ(ω)分别为微分Dν算子的幅频特性函数和相频特性函数,其表达式如下:

在式(3)幅频特性函数 α(ω)中,分别取 ν为0.1,0.5,0.8 和1,将 α(ω)数字化如图1 所示。
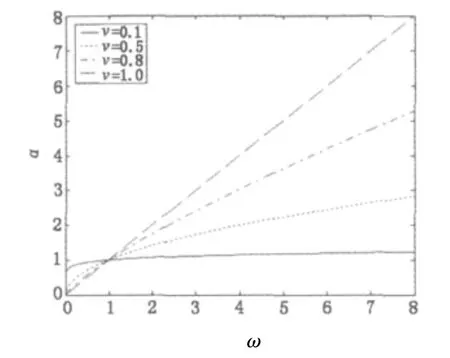
图1 微分算子的幅频特性曲线
从图1中可以看出,微分运算有提升高频信号的作用,并且随频率ω和微分阶次ν的增加,幅频特性曲线呈非线性增长。当ν=1为一阶微分算子,利用一阶微分算子处理图像虽然能大幅增加图像边缘高频成分,但是对图像中灰度变化不大的纹理细节信息中低频部分必然会大幅的线性衰减,其结果约等于零。当0<ν<1时,其特性曲线为分数阶微分特性曲线,与ν=1的直线相比,分数阶微分特性曲线在信号高频成分增幅小于一阶微分算子,而在信号的中频和低频成分增幅大于一阶微分算子。因此,可利用分数阶微分增强图像的边缘,同时增强图像的纹理。
2.2 分数阶微分定义与算子
分数阶微分定义有多种,若信号s(t)∈[a,t](a<t,a∈R,t∈R),当 ν>0 时,信号s(t)非整型 ν阶微分G-L定义表达式:


针对二维数字图像f(x,y),定义坐标轴(x,y)方向上分数阶微分后向差分近似表达式分别为:
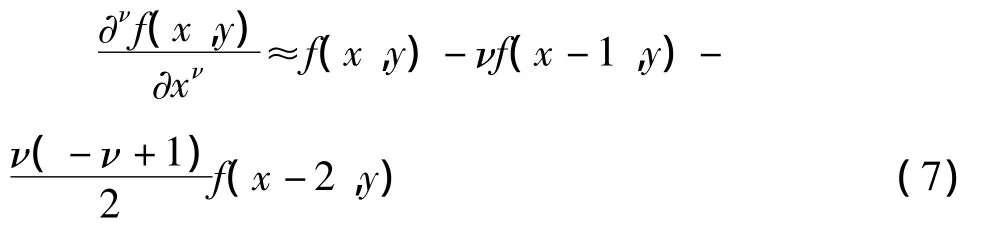
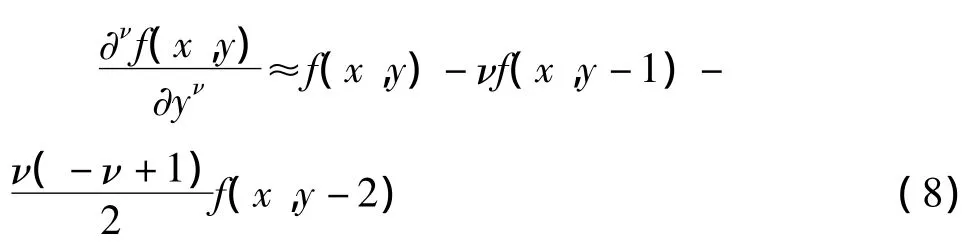
为了实现图像增强,选择分数阶差分定义的前3项作为二阶近似值,采用5×5模板:
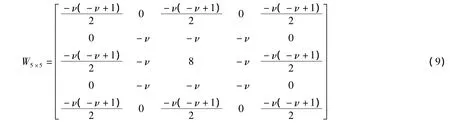
一般来说,对M×N的图像f(x,y)增强,可用m×n大小的模板进行对其线性滤波,增强后的图像g(x,y)表达为:
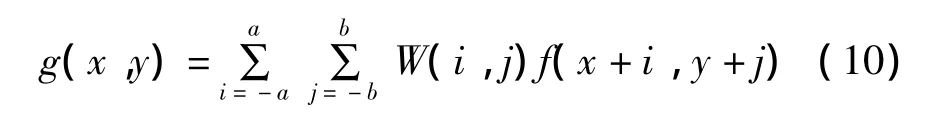
其中,a,b分别为分数阶微分算子模板大小在x,y坐标轴方向上的半径。
2.3 改进分数阶微分算子
根据式(10)分数阶算子增强图像纹理和边缘信息,为了使得增强的图像亮度不发生较大变化,首先将增强算子归一化,即W5×5的每项除以(8-12ν+4ν2),然后用分数阶算子增强算子对图像进行卷积运算。由于在平坦的光滑区域内,相邻点灰度值基本相同属于信号的甚低频部分,增强后输出灰度值的变化很小;在图像纹理区域,相邻点灰度值有变化属于信号的中、低频部分,输出灰度值将加强这种变化;在图像的边缘区域,邻近的灰度值变化较大属于信号的高频部分,输出灰度值将大大加强这种变化。最后利用分数阶微分算子处理后图像灰度值与原图像灰度值相减,得到图像经过分数阶微分增强信息值,通过对比分析说明由此获得的是具有很高信噪比的图像纹理和边缘信息。文献[9]提出将W5×5分成 0°,45°,90°,135°,180°,225°,270°和315°八个方向,例如为0°方向增强算子模板,归一化系数(1-1.5ν+0.5ν2)。将8个增强方向的最大值与W5×5增强值相比较,取其最大值视为增强后的图像。八方向示意图如图2所示。

图2 八方向示意图
对于一阶近似3×3模板W3×3为:
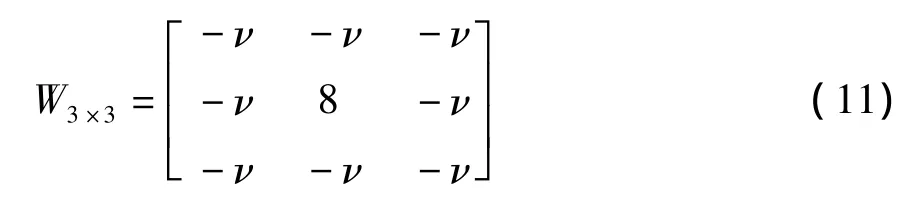
本文在3×3模板上的水平、垂直、正对角线和负对角线四个方向上,分别提出四个小模板分数阶微分算子:
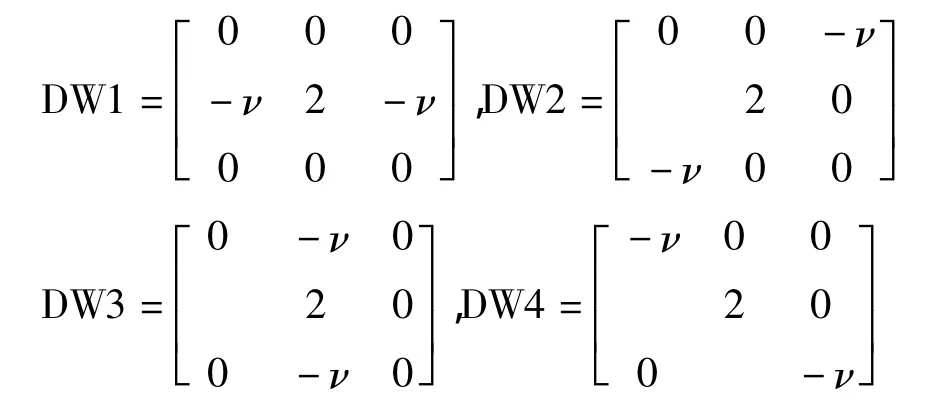
为了使得增强的图像亮度不发生较大变化,首先将增强算子 DW1,DW2,DW3和DW4归一化,即模板的每项除以(2-2ν),各模板中的常系数值“2”所在的坐标(x,y)和待进行分数阶微分的像素f(x,y)的坐标位置必须保持重合,将这4个方向上的模板上的系数值分别与输入的对应像素的灰度值相乘,然后将各自的所有乘积项相加(即加权求和),分别得到在这4个方向上的加权求和值,取4个增强方向的最大值视为增强后的图像。
3 分数阶微分图像增强效果对比
在下面实验中,分别采用文献[4]、文献[9]和本文算法对Lena中进行图像增强,其中分数阶微分为0.55 阶。
文献[4]运用分数阶微分二阶近似模板,在5×5窗口大小内取模板平均值为增强值。文献[9]将5×5模板划为八个方向的小模板,取小模板内加权和的最大值为中心点的增强值。本文改进方法运用分数阶微分一阶近似模板,将3×3窗口内划为四个方向的小模板,取小模板内加权和的最大值为中心点的增强值。从图3可知,图3(b)虽能突出边缘,但对帽子纹理和头发细节增强不够。图3(c)对立柱下方的边缘和帽子纹理和头发细节增强效果明显好于图3(b)。图3(d)对边缘、纹理和细节增强效果最好,尤其在图像右边的小撮头发和白色背景上方的纹理。

由于改进方法与中心点是1邻域,而文献[9]是2邻域。邻域半径愈大的像素,与中心点像素的相关性愈小。距离中心点远的像素会抑制中心点的变化,而距离中心点近的像素会扩大中心点的变化趋势。所以,改进方法增强效果明显好于其他方法。
图4为图3中第180行1~50列(在图3(a)左下方白线位置)的原图像灰度分布和三种方法增强后的图像灰度分布。如图4(a)所示在10~20列之间为立柱左边边缘,由于灰度值变化缓慢,图4(b)虽有增强但增强幅度不大,图4(c)增强效果较好,图4(d)增强效果最好。在第30列附近为立柱右边边缘,其灰度值变化较快,从图4可知,图4(d)增强效果最好,图4(c)增强效果次之,图4(b)也有明显的边缘增强效果。在第40~50列附近为头发细节,图4(d)对头发细节增强效果与灰度值变化较快的边缘增强效果一样且最好,图4(c)增强效果次之,而图4(b)对头发细节的增强效果不如对灰度值变化较快的边缘。
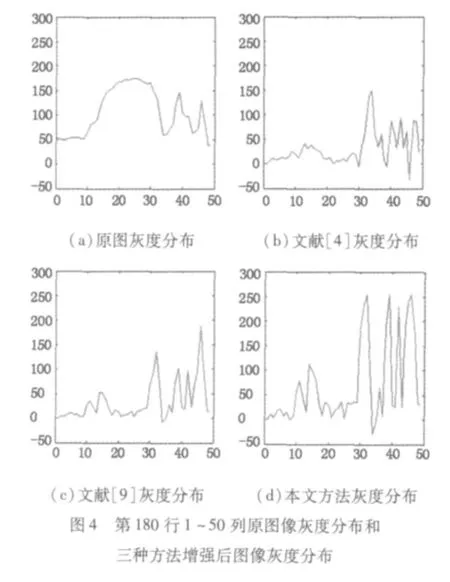
可见在文献[4]的方法中运用分数阶微分5×5模板内平均值为增强值,对边缘增强效果好于对纹理和细节信息的增强效果。由于边缘和纹理具有方向性,文献[9]将5×5模板划为八个方向的小模板,取小模板内加权和的最大值为中心点的增强值,对边缘和纹理细节有同样的增强效果,但增强不明显。考虑到边缘和纹理具有方向性,以及模板窗口越小,模板窗口内像素点的灰度值关联性越大,本文采用3×3模板窗口并将其划为四个方向的小模板,取小模板内加权和的最大值为中心点的增强值,对边缘和纹理细节有同样的增强效果,且增强幅度最大、效果最明显。
为定量评价图像增强效果,本文定义图像清晰度(Definition)如下:

其中,u为各种算法增强后的图像灰度值;m1,n1,m2,n2为窗口坐标。图像清晰度取值越大表明图像增强效果越好。表1为Lena图像以及尺寸为4、方差分别为 0.3,0.5,0.7 高斯模糊后,对模糊图像采用三种增强方法增强后的图像清晰度。从表1可知,三种增强方法对原图增强后,本文算法清晰度最大,文献[9]次之,文献[4]最差,与图3的视觉效果相符。随着高斯模糊方差增加,本文清晰度还是最大,文献[4]最差,但其清晰度相应比对原图增强后清晰度小,增强效果差。
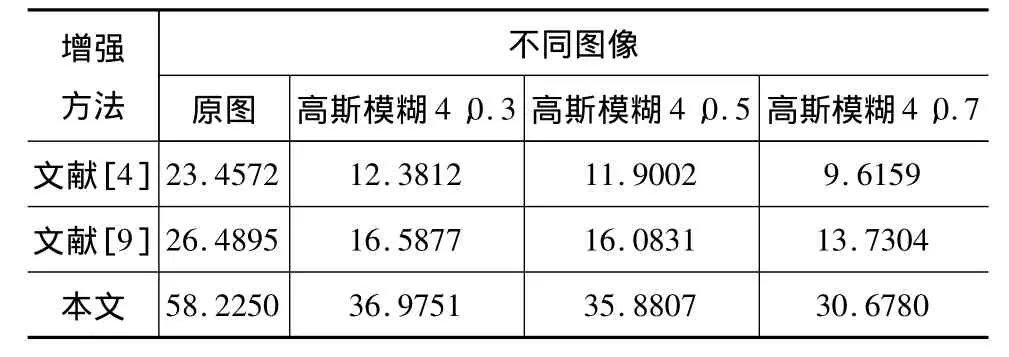
表1 图像清晰度
4 结束语
本文在G-L分数阶微分基础上构造了ν阶分数阶空域微分增强算子,并用数字算法实现了该分数阶微分算子。实验表明,在相同的5×5模板窗口大小中,八方向加权和的最大值增强算法效果优于模板内平均值增强效果;模板窗口越小,模板窗口内像素点的灰度值关联性越大,3×3模板窗口四个方向加权和最大值增强算法效果最好;本文提出的分数阶增强算子能明显地增强图像的纹理和边缘信息,增强后图像清晰度提高,视觉效果明显。
[1] Xu Weichang,HuangWei,Li Yongfeng,et al.Application of low-pass filtering and gray adjusting to image enhancement[J].Laser& Infrared,2012,42(4):458 -462.(in Chinese)
徐卫昌,黄威,李永峰,等.低通滤波与灰度值调整在图像增强中的应用[J].激光与红外,2012,42(4):458-462.
[2] Pu Yifei,Wang Weixing.Fractional differential masks of digital image and their numerical implementation algorithms[J].Acta Automatica Sinica,2007,33(11):1128 -1135.(in Chinese)
蒲亦非,王卫星.数字图像的分数阶微分掩模及其数值运算规则[J].自动化学报,2007,33(11):1128-1135.
[3] Pu Yifei.Application of fractional differential approach to digital image processing[J].Journal of Sichuan University:Engineering Science Edition,2007,39(3):124 -132.(in Chinese)
蒲亦非.将分数阶微分演算引入数字图像处理[J].四川大学学报:工程科学版,2007,39(3):124-132.
[4] Yang Zhuzhong,Zhou Jiliu,Yan Xiangyu,et al.Image enhancement based on fractional differentials[J].Journal of Computer-Aided Design & Computer Graphics,2008,20(3):43 -348.(in Chinese)
杨柱中,周激流,晏祥玉,等.基于分数阶微分的图像增强[J].计算机辅助设计与图形学学报,2008,20(3):43-348.
[5] Pu Yifei,Zhou Jiliu,Yuan Xiao.Fractional differentia mask:a fractional differential-based approach for multiscale texture enhancement[J].IEEE Transactions on Image Processing,2010,19(2):491 -511.
[6] Pu Yifei.Research on application of fractional calculus to latest signal analysis and processing[D].Chengdu:Sichuan University,2006.(in Chinese)
蒲亦非.分数阶微积分在现代信号分析与处理中应用的研究[D].成都:四川大学,2006.
[7] Wang Chengliang,Lan Libin,Zhou Shangbo.Adaptive fractional differential and its application to image texture enhancement[J].Journal of Chongqing University,2011,34(2):32 -36.(in Chinese)
汪成亮,兰利彬,周尚波.自适应分数阶微分在图像纹理增强中的应用[J].重庆大学学报,2011,34(2):32-36.
[8] Yan Xiangyu,Zhou Jiliu.Fractional calculus applied to medical image processing [J].Journal of Chengdu University of Information Technology,2008,23(1):39 - 41.(in Chinese)
晏祥玉,周激流.分数阶微积分在医学图像处理中的应用[J].成都信息工程学院学报,2008,23(1):39-41.
[9] Wang Weixing,Yu Xin,Lai Jun.An improved fractional differentialmask[J].Pattern Recognition and Artificial Intelligence,2010,23(2):171 -175.(in Chinese)
王卫星,于鑫,赖均.一种改进的分数阶微分掩模算子[J].模式识别与人工智能,2010,23(2):171 -175.
