永磁直线电机扰动力的在线辨识与补偿
2013-11-12孙静娜葛晓宇潘佩琦
孙静娜,肖 勇,葛晓宇,潘佩琦
(沈阳化工大学 信息工程学院,辽宁 沈阳 110142)
高精度运动系统的永磁直线电机(PMLM)采用高能永磁体,具有推力强度高、损耗低、电气时间常数小、响应速度快等特点,因此,在高档数控机床进给驱动中得到了广泛的应用,并成为新一代数控机床的主要标志之一[1].针对数控机床中的高精度和微进给要求,在运动控制过程中,需要充分考虑若干非确定性扰动因素的影响,尤其是扰动力的存在会增大系统的同步误差.因此,本文首先建立直线电机及扰动力的数学模型,其次运用递归最小二乘法对电机参数及扰动力的参数进行在线辨识,最后设计了扰动力的前馈补偿器,以降低扰动对系统同步性能的影响.
1 PMLM 建模
典型永磁直线电机可以分为线性部分和不定非线性部分,如图1 所示.其动力学方程可以表示为[2]:

这里y(t)和u(t)分别表示电机位置输出和控制输入,Ia表示电枢电流,Va是粘度常数,Ra表示电枢电阻,La表示电枢电感,Kf表示电机输出能量系数,Kβ表示电磁场的返回电压,Ku表示放大器增益,m 是滑块质量,Fd为系统干扰,包括模型不确定因素,如扰动力、摩擦力及负载等.
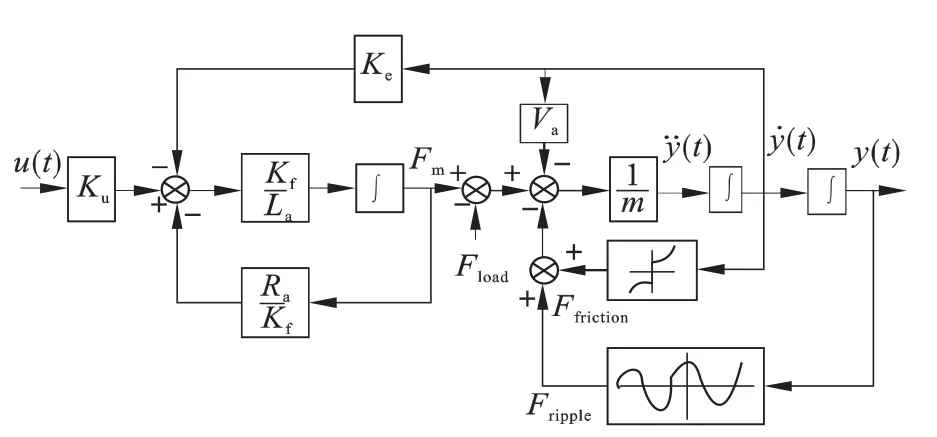
图1 PMLM 框图Fig.1 Block diagram of the PMLM
定义

则式(1)可简写为

电机的阶跃响应曲线如图2 所示.显然,电机速度的扰动是电机位置信号的周期性函数,波动频率为恒值,而幅值随电机控制输入的变化而变化[3].因此,扰动力的一阶模型可由下式描述:
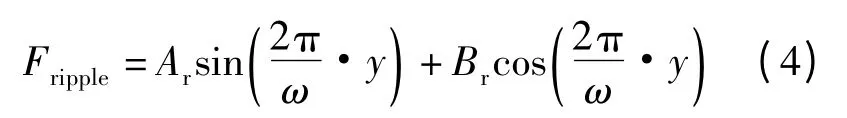
这里Ar、Br代表扰动力振幅,ω 为扰动力频率.

图2 永磁直线电机的速度与位置关系Fig.2 The relationship of velocity and position of PMLM
2 系统辨识及前馈补偿
通过不同输入的阶跃响应测试,可以估计出扰动力固有频率[4]:ω1=2π/0.074 4 和ω2=2π/0.051.在此不考虑摩擦力和负载力,这样系统模型可进一步简化为:

这里i=1,2 表示系统的电机序号,延迟时间t1=0.001 6 s 和t2=0.000 8 s.为了避免速度vi(t)的微分求解,在式(6)中引入了稳定的滤波器Hf,例如=(sHf)vi(t),使得式(6)可转化为:

其中,yfi=Hf˙yi(t),vfi=Hfui(t-ti).
分别定义未知参数向量和回归向量为:

则系统参数的递归最小二乘辨识算法可描述如下:

其中滤波器Hf选择这样随着系统的运行,就可以在线辨识出系统未知参数和扰动力幅值.由于扰动力会降低系统的运动性能,因此,一个简单而有效的解决方法就是引人一个对消项,即扰动补偿[5].由扰动力模型可知,通过测试PMLM 的动态特性,逐点测试可得出扰动力的非线性曲线,这样扰动辨识模型与系统参数b的商构成扰动补偿器.用Δu 表示扰动力前馈补偿部分,其计算公式如下:

其中Fripple中的参数Ari、Bri及系统的参数b 均来自在线参数辨识结果.
在控制输入端嵌入扰动力前馈补偿器,对扰动力进行动态补偿,以消除扰动力对系统同步性能的影响[6],其控制框图如图3 所示,此系统包含了两个独立运行的直线电机.
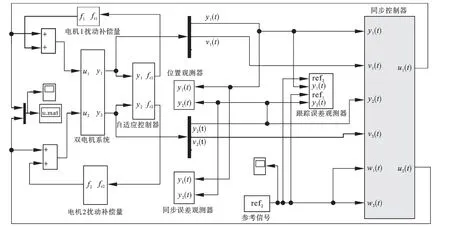
图3 同步控制系统仿真Fig.3 Simulation of synchronous control system
3 仿真实验结果
实验所选电机1 和电机2 的参数分别为:M1=10 kg,B1=1.2 N·s/m,Kf1=25 N/m,Fln1=40 N,M2=5.4 kg,B2=20.8 N·s/m,Kf2=130 N/m,Fln2=26 N.为了满足位置跟踪超调小和稳态静差小的要求,设置预测控制器参数为:预测域Np=10,控制域Nu=5,控制输入权重系数λ=0.02,同步系数ϑ=1.表1 为系统参数辨识结果.图4 为无扰动补偿时系统的输入仿真结果,图5 为有前馈补偿时系统的位置输入仿真结果.由此可见,系统在扰动补偿后,控制输入没有明显的波动,变化较为平滑,系统具有很强的抗干扰能力.图6 为有、无前馈补偿时2 个电机之间的同步误差曲线,通过前馈补偿,系统的同步性能也得到了较大的提升,同步误差从1 μm 左右减小到0.1 μm 左右,同时增强了系统的鲁棒性.

表1 系统参数辨识结果Table 1 The identfication of system parameters

图4 无前馈补偿时控制输入电压Fig.4 The control input without feed-forward compensation

图5 有前馈补偿时控制输入电压Fig.5 The control input with feed-forward compensation
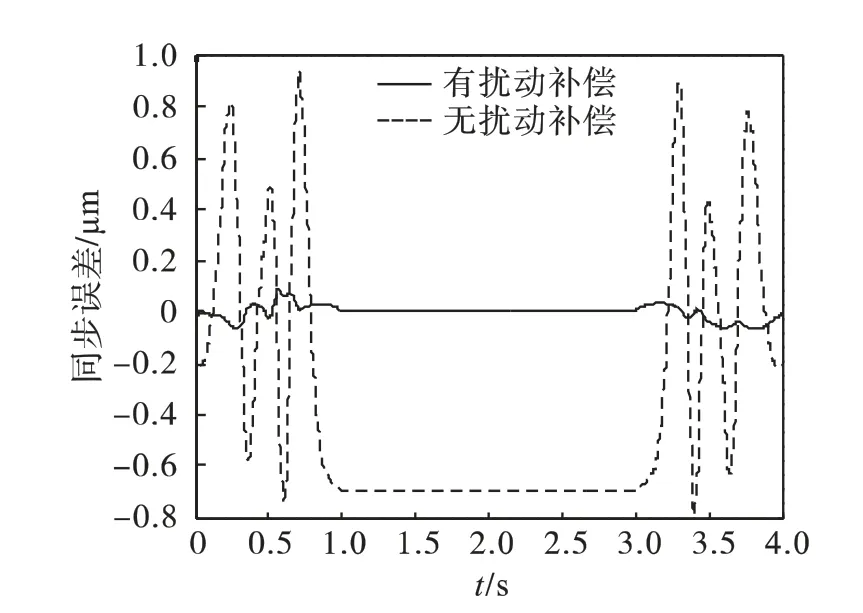
图6 有无前馈补偿时同步误差比较Fig.6 Comparison of the synchronous error with/without feed-forward compensation
4 结束语
提出了基于参数辨识和扰动力前馈补偿的PMLM 的位置控制器,其仿真结果表明:所设计的控制系统能实现对位置参考信号的快速无超调跟踪,同时将两个电机的同步误差从1 μm 左右进一步缩小到0.1 μm,且稳态误差大幅度减小.因此,系统能够自动适应环境参数的变化和增强抗扰动能力,以满足高精度、微进给永磁直线电机驱动系统的高控制性能要求.
[1]XIAO Y,ZHU K Y,ZHANG C,et al.Stabilizing Synchronization Control of Magnetic Bearing-based Flywheel Energy Storage Systems[C].Kunming:PROCEEDINGS OF THE 8th International Conference on Control,Automation,Robotics and Vision,2004:1711-1716.
[2]YEH S S,HSU P L.Analysis and Design of Integrated Control for Multi-axis Motion Systems[J].IEEE Transactions on Control System Technology,2003,11(3):375-382.
[3]QIN S J,BADGWELL T A.A Survey of Industrial Model Predictive Control Technology [J].Control Engineering Practice,2003,11(7):733-764.
[4]XIAO Y,ZHU K Y,LIAW H C.Generalized Synchronization Control of Multi-axis Motion Systems[J].Control Engineering Practice,2005,13(7):809-819.
[5]XIAO Y,ZHU K Y,ZHANG C,et al.Stabilizing Synchronization Control of Rotor-magnetic Bearing Systems[J].Journal of Systems and Control Engineering,2005,219(7):499-510.
[6]TAN K K,LEE T H,DOU H F,et al.Precision Motion Control:Design and Implementation (Advances in Industrial Control)[M].London:Springer-verlag,2001:25-36.
