BP神经网络估计IRT参数的比较研究

刘 文 边玉芳 陈玲丽 阳碧云

1 引言

与经典测量理论相比，项目反应理论（IRT）采用非线性的模型建立被试在项目上的得分与潜在特质之间的关系，具有题目参数的跨群体不变性、能力参数与项目难度参数定义在同一个量表上等优良性质，这为项目反应理论的推广应用奠定坚实的基础。但是由于项目反应理论模型的复杂性，带来相应的参数（题目参数、能力参数）估计相对困难，在进行参数估计时通常要经过多次复杂的迭代运算，进行运算时通常要求较大的样本容量，并且还有可能的情况是得到的结果不收敛。

人工神经网络（Artificial Neural Networks，ANN）也称为“神经网络”或类神经网络，是一种应用类似于人类大脑神经突触联接的方式进行信息处理的数学模型，它是以对大脑的胜利研究成果为基础，通过模拟大脑的某些机制，从而实现特定的功能，它是当前国内外研究的一个前沿领域。人工神经元是人工神经网络基本的信息处理单元，人工神经网络通过对大量人工神经元按照一定的拓扑结构组织起来，形成群体并行式处理的计算结构。神经网络已经应用于模式识别、图像处理、控制和优化、预报和智能信息管理、通信、空间科学等领域，显示出无可比拟的优势和应用前景。BP神经网络是一种多层前馈型神经网络，可以实现从输入值到输出值的任意非线性映射，其权值的调整采用反向转播学习算法，目前在神经网络的实际应用中，绝大部分的神经网络模型都采用BP网络及其变化形式。在IRT参数估计时，也有学者运用神经网络进行IRT的参数估计[1-4]，神经网络对于小样本的参数估计也能适用[5，6]，这些方法在使用神经网络时通常以经典测量理论中的通过率P作为难度的输入值、点二列相关系数rpb作为区分度的输入值、题目平均得分作为能力的输入值，相应的IRT参数b、a、θ作为神经网络的输出值来训练神经网络，然后使用训练好的神经网络进行新项目的参数估计，采用训练好的神经网络进行IRT的参数估计也能达到一定的误差要求。

文中提出根据经典测量理论计算的难度、区分度进行相应的转换，在BP神经网络中运用与前人研究不同的输入值估计IRT的项目参数的新方法，试图减少参数估计的误差，提高参数估计的精度。

2 IRT模型

项目反应理论通常使用一定的数学模型来刻画被试的得分与潜在特质的关系，项目反应理论模型通常分为二值记分的模型和多值记分的模型，其中最常用的是二值记分（0-1）的模型，二值记分的模型又分为单参数、双参数和三参数模型，二值记分的三参数的 logistic 模型为：pi（θ）=ci+（1-ci）/（1+exp[-Dai（θ-bi）]），这里D=1.702，θ为被试的能力值，ai表示项目 i的区分度、bi表示项目 i的难度、ci表示项目i的猜测参数，pi（θ）表示能力为θ的被试答对区分度为a、难度为b、猜测参数为c的项目i的概率，当被试答对该题时，得分为1，否则为0。在该模型中，当ci=0时为双参数模型，当ci=0、ai=1时为单参数模型。假设有N个考生参加由m个项目组成的测验，所有考生对各个项目的反应就组成一个Nm的得分矩阵U，参数估计就是寻找一组项目参数和被试的能力参数，代入IRT模型后，能够与项目反应得分矩阵U拟合得很好，在该矩阵中有N+3m个参数需要估计，这显然是一件非常困难的事情。伯恩鲍姆（1968）建议先计算能力参数、项目参数的初值，然后分两步进行迭代计算[7]：第一步，先假定能力参数为已知，求出项目参数的估计值；第二步，将项目参数的估计值看做项目参数的“真值”，求能力参数的估计值，这样前后两步称为一轮。如果满足收敛准则，则得到的项目参数和能力参数为所求的结果；否则，将这些值看做新一轮的初值，再进行下一轮的两步迭代，直到结果满足收敛准则为止。目前的参数估计方法例如MLE、EM、MCMC等都是根据伯恩鲍姆的这一思想进行的。

3 基于神经网络的IRT参数估计方法

文中设a、b、θ服从如下分布：能力参数θ～N（0，1），即生成被试的能力参数θ服从均值为0，方差为1的正态分布；ln a～N（0，1），b～N（0，1）。使用MATLABR2007b软件模拟生成N个被试作答m个项目的数据，a、b、θ满足上述条件。研究中采用四层的神经网络，节点数依次为10、7、3、1，前三层采用S型函数（tansig），最后一层采用线性函数（purelin）[2]。为了便于描述，以下只分两种方法进行介绍，方法一为分别以经典测量理论的通过率、点二列相关系数和平均得分作为网络输入估计a、b、θ，方法二为分别以IRT模型参数估计的初值作为网络输入估计a、b、θ。

3.1 能力参数θ的估计

方法一：利用平均得分率作为网络输入，IRT的θ为输出值，训练并测试网络。

（1）模拟。根据模拟生成的N个被试能力参数和m个项目参数计算 pi（θ），使用蒙特卡罗方法生成被试得分矩阵U，当rij≤pij时，uij=1，否则uij=0。随机生成30个得分矩阵。

（2）降维。根据得分矩阵U，计算每名被试对m个项目的平均得分（x/m）作为神经网络的输入向量，以模拟被试的能力θ为神经网络的输出值训练神经网络。将30个平均得分向量作为网络输入训练30个网络。

（3）测试。模拟生成N1个被试能力参数和m1个项目参数计算，生成得分矩阵，计算每名被试对m1个项目反应的平均得分（x1/m1）作为神经网络的输入向量，测试训练好的神经网络进行被试能力输出。分别测试训练好的30个神经网络。计算每次测试网络输出值与模拟数据的能力值的误差，即error=yy-θT，yy为神经网络的输出值，θT为模拟生成的N1个被试的能力值。

方法二：利用N-R迭代求能力参数的极大似然估计的初值θ0作为网络输入，IRT的θ为输出值，训练并测试网络。

（1）模拟。与3.1.1方法一模拟相同。

（2）降维。与3.1.1方法一的区别是输入向量不同，输入向量为每名被试对m个项目的得分（x）与失分（m-x）之比的自然对数ln[ ]x/（m-x）作为神经网络的输入向量（对总分为满分和零分的被试进行预处理，依据Conquest软件的处理方法，满分则减去0.3，0分则加上0.3）。

（3）测试。与3.1.1方法一的区别是输入向量不同，ln[x1/（m1-x1）]作为神经网络的输入向量进行测试。

项目参数a、b的两种估计方法与能力的两种估计方法类似。

3.2 项目参数a的估计

方法一：利用每个项目与总分的点二列相关系数作为网络输入，IRT的a为输出值，训练并测试网络。

（1）模拟。与3.1.1方法一模拟相同。

（2）降维。计算项目得分矩阵U中每个项目与总分的点二列相关系数

（3）测试。与3.1.1方法一的区别是输入向量不同，点二列相关作为神经网络的输入向量进行测试。

方法二：利用IRT参数估计的初值aj作为网络输入，IRT的a为输出值，训练并测试网络。

（1）模拟。与3.1.1方法一模拟相同。

（2）降维。与3.2.1方法一的区别是网络输入的初值为aj，aj通过点二列相关转化得到，具体为：根据得分矩阵U计算每个项目的通过率pj，并根据通过率pj转化为标准正态分数zj，即根据计算出zj。再把点二列相关rpb转化为二列相关rb，其公式为最后，求得输入向量aj，即利用aj作为网络输入向量训练网络。

（3）测试。与3.2.1方法一的区别是输入向量不同，aj作为神经网络的输入向量进行测试。

3.3 项目参数b的估计

方法一：利用每个项目的通过率作为网络输入，IRT的b为输出值，训练并测试网络。

方法二：区别在于计算网络输入向量bj时，公式为bj=zj/rbj，利用bj作为网络输入，IRT的b为输出值，训练并测试网络。

4 实验结果

评价参数估计精确性的指标通常采用均方根误差（Root Mean Squared Error，RMSE）（有些文献称为RMSD）和平均绝对偏差（Mean Absolute Bias，MAB）（有些文献称为ABS）这两个指标，表示估计值的个数，r表示网络数。MAB指标反映了估计值与真值的绝对偏差的平均。MAB值越小，估计的准确性越高；RMSE指标反映的是估计值与真值偏差的离散程度。RMSE值也是越小越好。

实验中训练网络时，训练项目数分别取10、20、30、…、590、600（共60种实验条件），训练人数为100人；测试网络时，测试时项目数为20题，人数为100人。每种实验条件是循环30次后结果的平均值。

以MAB和RMSE作为不同方法估计精确度的指标，分别比较两种方法在估计IRT两参数模型中能力参数和项目参数的差异。

4.1 MAB指标分析结果

神经网络不同输入向量对能力参数和项目参数估计的MAB指标分析结果见表1。

表1 能力参数和项目参数估计的MAB指标描述统计分析结果

从表1可以看出，对于难度的估计以通过率作为神经网络的输入值比经过转换后的输入值能得到更好的结果，而区分度和能力值的估计则是经过转换后的输入值的结果更精确。

4.2 RMSE指标分析结果

神经网络不同输入向量对能力参数和项目参数估计的RMSE指标分析结果见表2。

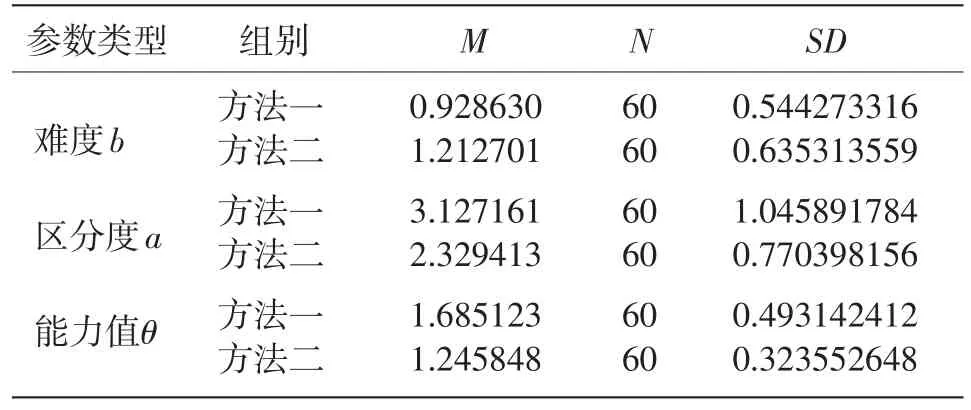
表2 能力参数和项目参数估计的RMSE指标描述统计分析结果

从表2可以看出，对于难度的估计以通过率作为神经网络的输入值比经过转换后的输入值能得到更好的结果，而区分度和能力值的估计则是经过转换后的输入值的结果更精确。

综合表1、表2的结果，表明MAB和RMSE的结论具有一致性。

5 结束语

实验表明，基于经典测量理论基础上转换后的输入值的区分度和能力参数的估计，神经网络参数估计的方法具有较高的精确度与稳定性；而难度参数的估计则是通过率占优。但对于神经网络模型来说，估计的精确性不仅与网络的输入值有关同时还与神经网络的类型也有关系，例如采用径向基网络进行模拟训练可能会得到不同的实验结论，这些需要进一步的研究证据支持。由于研究中主要探讨两参数的项目反应模型，这个结论是否适用于三参数的项目反应模型仍需相关证据。同时，研究采用的是简单的0-1评分的模型，对于多值评分的模型如何使用神经网络进行估计也值得探讨。

[1]谭云兰，丁树良，辛锐铭，等.基于IRT模型参数的BP神经网络估计[J].计算机工程与应用，2004（17）:56-57，108.

[2]谭云兰，丁树良，辛锐铭.基于IRT模型的BP神经网络降维法参数估计及其应用[J].江西师范大学学报（自然科学版），2004，28（6）:485-488.

[3]汪存友，余嘉元.一种新的基于神经网络的IRT项目参数估计模型[J].计算机应用，2006，26（4）:992-994.

[4]余嘉元，陈淑燕.运用径向基网络估计项目反应模型参数的研究[J].中国考试（研究版），2005（4）:24-26.

[5]余嘉元，汪存友.小样本标准参照测验中项目参数估计的GRNN方法[J].广西师范大学学报（自然科学版），2006，24（4）:107-110.

[6]朱隆尹，丁树良，涂冬波，等.基于小样本容量的IRT参数估计方法比较研究[J].心理学探新，2009，113（5）:72-76.

[7]漆书青，戴海崎，丁树良.现代教育与心理测量学原理[M].北京:高等教育出版社.2002.