钢丝绳结构测量及三维建模

2013-11-06虞强

机电工程技术 2013年11期

虞强

（攀钢集团攀枝花钢钒有限公司，四川攀枝花 617000）

0 前言

钢丝绳是起重机的重要零部件，也是易损件，做好钢丝绳的维护保养，提高钢丝绳使用过程中安全性，减少由钢丝绳引发的起重机械伤害事故，保障人员的安全，减少经济损失显得尤为重要。本文以起重机钢丝绳解体观察、测量和校核参数为基础，建立了钢丝绳曲线方程，利用Pro/E软件实现了钢丝绳三维空间模型的建立，便于工程技术人员能更好地掌握钢丝绳结构。

1 钢丝绳拆股测量

将新制钢丝绳36NAT 6*19W+IWR-ZS在长度上截取1米（如图1），清洗干净，进行拆股解体观察和测量。钢丝绳直径和股径的测量采用宽口钳游标卡尺，钢丝直径的测量采用游标卡尺，钢丝绳及各股的捻距测量采用卷尺。

1.1 钢丝绳结构测量

1.1.1 绳芯中心股结构测量

图1 截取钢丝绳的外形图

拆股后，观察发现钢丝绳绳芯中心股由6根钢丝围绕1根中心丝左向旋转而成，用卷尺测量其捻距t≈50.4 mm（如图2）。中心股的断面图见图2，可以看出中心股为单捻股结构形式，即只由一层钢丝捻制而成，其结构为6+1结构形式。用游标卡尺分别测量中心股和芯丝的直径，中心股直径D1=4.1 mm，中心丝半径R1=0.75 mm，外丝半径R2=0.65 mm。

1.1.2 绳芯的绳股结构测量

拆股解体后，发现钢丝绳绳芯外股由6股钢丝绳围绕中心股左向旋转，绳芯断面图见图3。绳芯外股每股钢丝绳围绕1根中心丝左向旋转而成，可见为单捻股结构形式，结构为6+1形式，其断面图见图4。

测得绳芯股绳的钢丝半径如下：

中心股直径D3=4.1 mm；

中心丝半径R5=0.75 mm；

外丝半径R6=0.65 mm。

测得绳芯外股和股绳的捻距如下：

绳芯外股捻距110 mm；

绳芯外股股绳捻距50.4 mm。

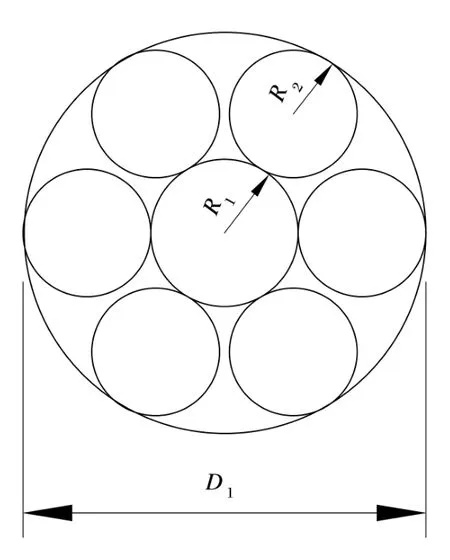
图2 中心股断面图

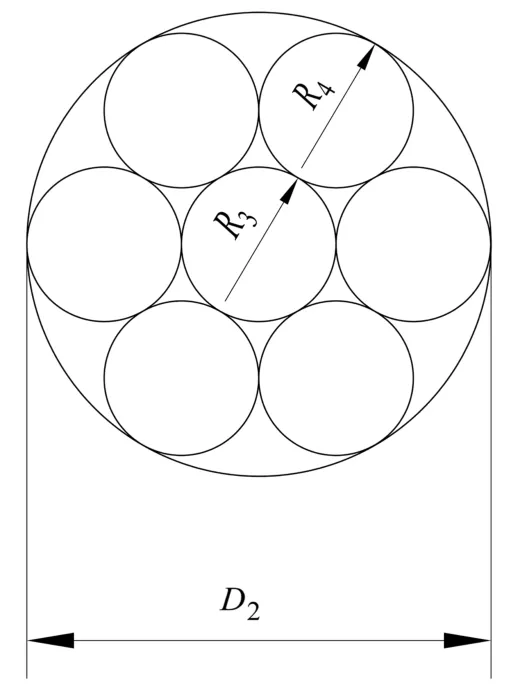
图3 绳芯绳股断面图

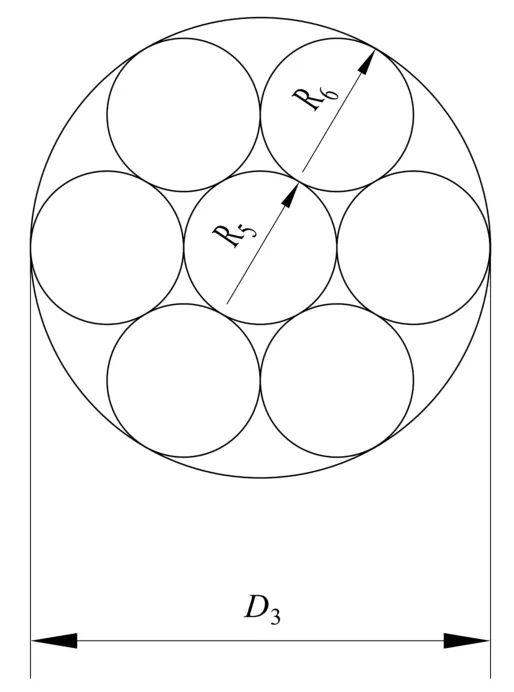
图4 绳芯侧股断面图

1.1.3 钢丝绳的外股结构测量

拆股观察可以看出，钢丝绳由6股绕中心钢芯左向旋转而成（如图5），每股钢丝绳股由3层钢丝组成，外层由6根粗丝和6根细丝交替组成，中间层右6根相同直径的钢丝组成，内层由1根钢丝构成，外层和中间层钢丝绕内层钢丝右向旋转，钢丝绳外股断面如图6。

测得外股的钢丝半径如下：

中心丝半径R9=1.3 mm；

第二层丝半径R10=1.25 mm；

第三层细丝半径R11=1.175 mm；

第三层粗丝半径R12=1.35 mm。

测得绳芯外股和股绳的捻距如下：

钢丝绳外股捻距210 mm；

钢丝绳股绳捻距120 mm。

从以上拆股观察的结果来看，该钢丝绳的断面图如图7，钢丝绳为双捻钢丝绳，外层由6股右捻的1×19单捻钢丝绳绕内层钢芯左向旋转，每股结构为1+6+6/6，内层钢芯由6股左捻的1×7单捻钢丝绳绕内层1×7左捻的钢丝绳左向旋转，每股结构为6+1，钢丝总数为163（外层114，钢芯49）。

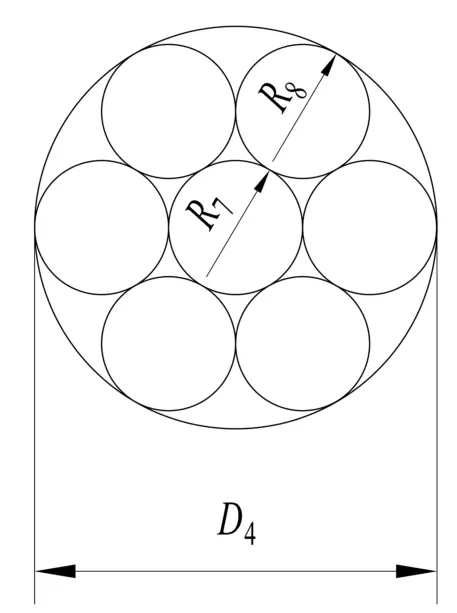
图5 钢丝绳股绳断面图

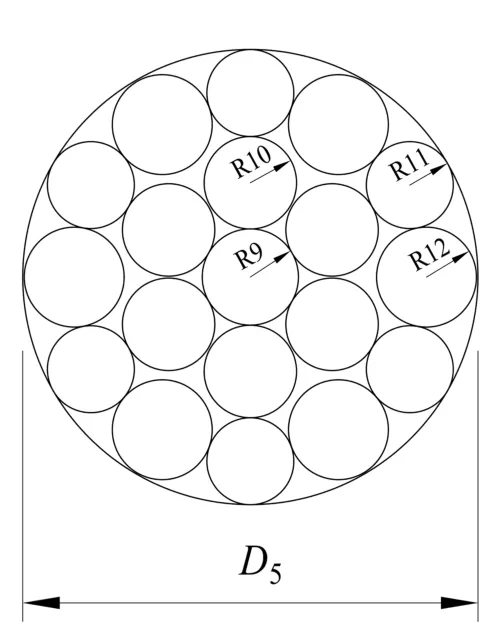
图6 钢丝绳外股断面图

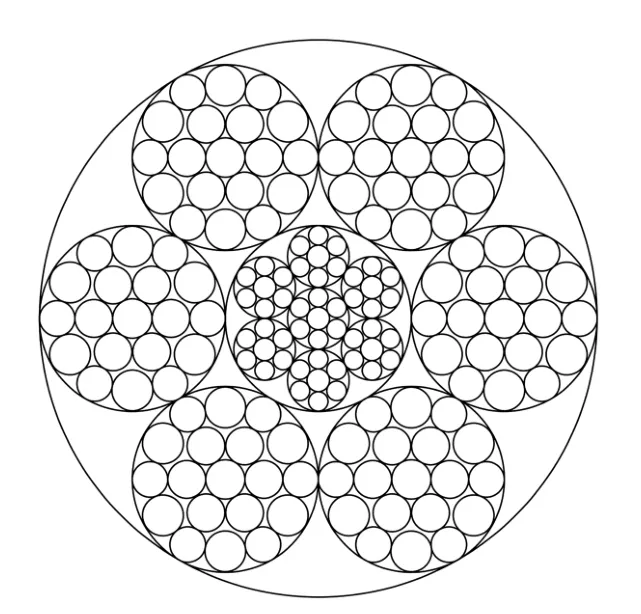
图7 钢丝绳断面图

1.2 设计捻距校核

1.2.1 绳芯捻距校核

由于中心股的捻距测量值t≈50.4 mm，中心股的直径d=4.1 mm。由文献[1]公式1-2知：

k=t/d=50.4/4.1=12.29

式中：k——股的捻距倍数；

t——股绳捻距；

d——股绳直径。

设计时捻距倍数一般为整数，因此取整后捻距倍数为12。

则设计捻距为：12×4.1=49.2 mm。

同理，计算出钢芯外股捻距倍数为9，校核后的设计捻距为110.7 mm。

1.2.2 其余捻距校核

采用2.2.1的计算方法，计算出钢丝绳外股捻距倍数为10，校核后的设计捻距为118.5 mm。钢丝绳外股捻距倍数为6，校核后的设计捻距为216 mm。

1.3 捻角计算

1.3.1 绳芯外丝捻角计算

1.3.2 其余捻角计算

采用2.3.1的计算方法，求得绳芯外股的捻角为13.094°，钢丝绳外股钢丝的捻角为18.2499°，钢丝绳外股的捻角为20.837°。

1.4 钢丝绳曲线方程

1.4.1 钢丝绳各钢丝的曲线公式推导

以右交互捻的钢丝绳为例，建立如图8所示的钢丝空间曲线矢量图[2]。在整体坐标系（O，X，Y，Z）中，若一次螺旋线上的点q的位置用Q表示，二次螺旋线上的点p的位置用P表示。由图8知，矢量P可表达为

由一般螺旋线定义可知，矢量Q的表达为

式（2）中：R——一次螺旋线的半径；

θ——为q点在一次螺旋线中的极角；

α——一次螺旋线的螺旋升角。

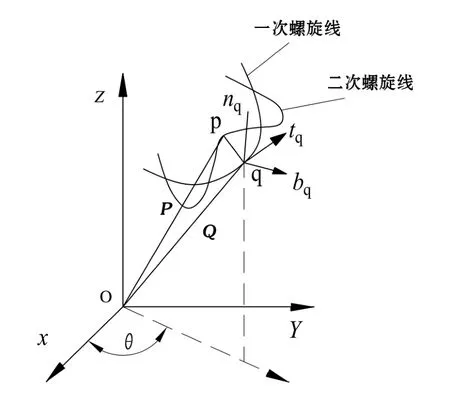
图8 钢丝空间曲线矢量图

建立一次螺旋线上q点的Frenet标架nq-bq-tq，nq平行于O，X，Y平面。外层钢丝与钢丝绳的旋向相反，因此，矢量PQ在此Frenet标架中的表达式为：

式（3）中：r——二次螺旋线的半径；

φ——P点在二次螺旋线的极角。

由式（3）求解可得矢量PQ在整个（O，X，Y，Z）中的表达式为：

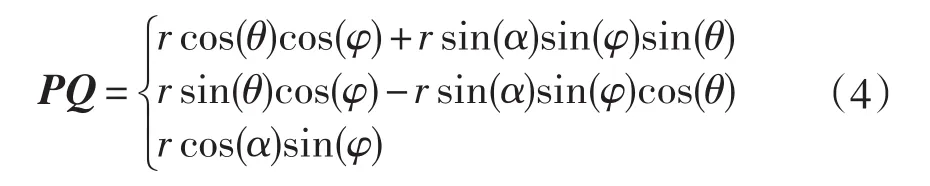
由公式（1）、（2）和（4）求解可得矢量P的表达式为：

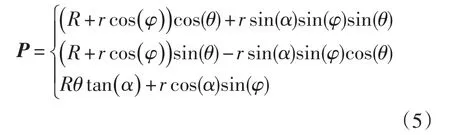
公式（5）即为右交互捻钢丝绳钢丝中心曲线方程。改变公式（3）矢量PQ的表达式，推导可得左交互捻钢丝绳钢丝中心曲线方程。

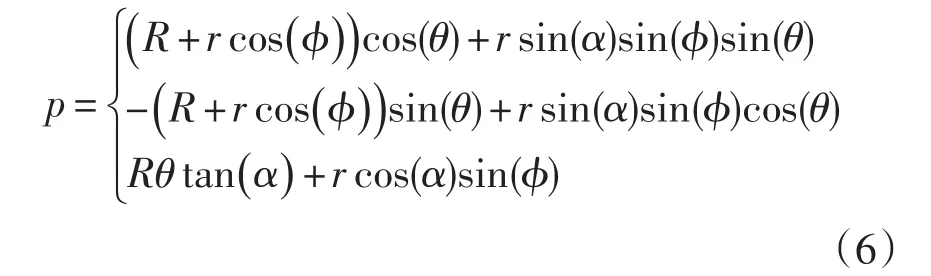
1.4.2 各钢丝的迪卡尔坐标系方程式

因Pro/E插入曲线时只支持迪卡尔、圆柱和球坐标系，为此需将钢丝的空间曲线转换为笛卡尔坐标系[3-4]，各钢丝的笛卡尔坐标系方程式如下：

（1）钢芯中心股中心丝

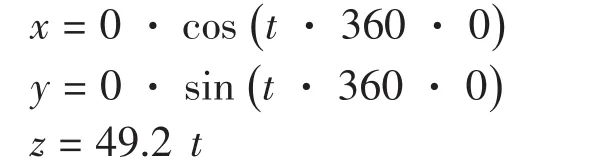
（2）钢芯中心股侧丝

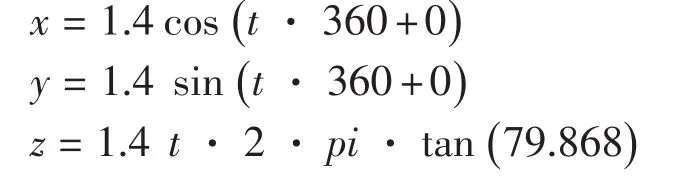
（3）钢芯外股中心丝

（4）钢芯外股侧丝

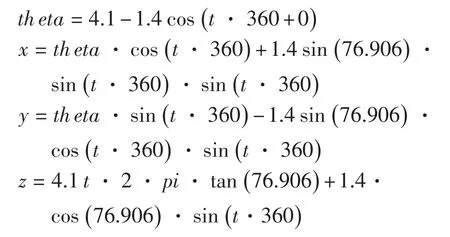
（5）钢丝绳外股中心丝

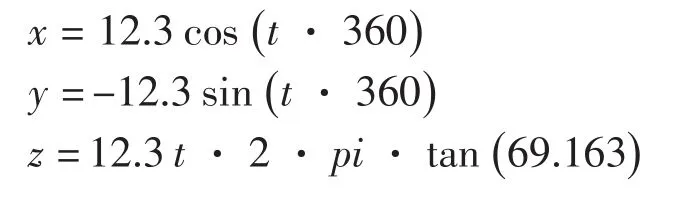
（6）钢丝绳外股第2层丝

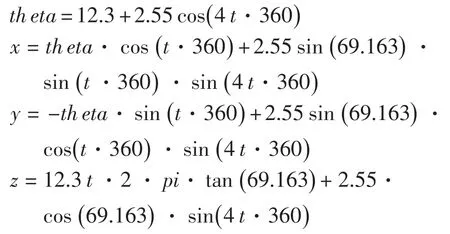
（7）钢丝绳外股第3层粗丝

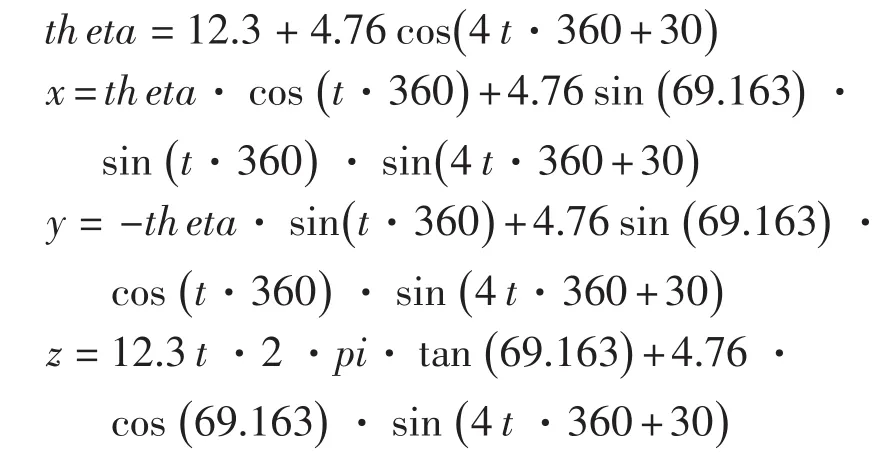
（8）钢丝绳外股第3层细丝

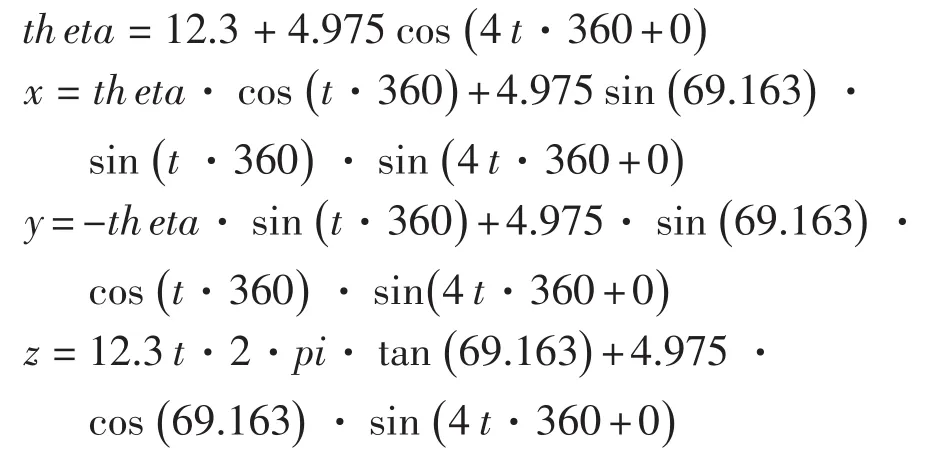
改变相关的几何参数，可得到钢丝绳每根钢丝在笛卡尔坐标系中的方程式。

2 模型的建立

利用Pro/E支持公式插入曲线的功能，插入钢丝绳曲线方程得到各钢丝的曲线，从而完成钢丝绳各钢丝的空间三维曲线。

打开Pro/E，新建实体，选择菜单，单击插入，选择模型基准，插入基准曲线，从方程，完成，选取迪卡尔坐标系，进入方程编辑，输入曲线x，y，z方程式，即完成钢丝曲线的创建。

经过上述过程，分别输入各钢丝完成钢丝绳各钢丝的曲线x，y，z方程式。即可完成钢丝绳各钢丝的曲线创建，如图9。然后选菜单，插入，可变截面扫描，参照，选取轨迹，在图形中选取单根钢丝的曲线，进入草绘模式，根据单根钢丝的位置、直径等绘制草图，完成单根钢丝的创建。用同样的方法完成其他钢丝的创建，从而完成钢丝绳的三维实体建模，钢丝绳的三维实体模型如图10。