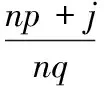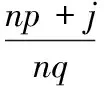一个数论命题及其应用
2013-11-06宋述刚长江大学信息与数学学院湖北荆州434023
宋述刚 (长江大学信息与数学学院,湖北 荆州 434023)
文昌敏 (荆州市沙市教育科学院,湖北 荆州 434000)
一个数论命题及其应用
宋述刚 (长江大学信息与数学学院,湖北 荆州 434023)
文昌敏 (荆州市沙市教育科学院,湖北 荆州 434000)
建立了如下数论命题:设p,q∈N+,0 互素; 整除 ;有界函数 在华东师范大学数学系编写的《数学分析》有如下一道习题[1]: 例1设: 证明:∀x0∈(0,1)与δ>0,满足(x0-δ,x0+δ)⊂(0,1),都有函数f(x)在(x0-δ,x0+δ)上无界。此处(p,q)表示p,q的最大公约数,(p,q)=1表示p,q互素。 由此,笔者考虑如下数论命题。 猜想1设p,q∈N+, 0 (mp+j,mq)=1 但遗憾的是,此猜想并不成立,有如下反例。 例2[2-3]取p=3,q=7,m=6!×5=3600,可以计算: (3×3600+1,7×3600)=7 (3×3600+2,7×3600)=2 (3×3600+3,7×3600)=3 (3×3600+4,7×3600)=4 (3×3600+5,7×3600)=5 (3×3600+6,7×3600)=6 即: (3×3600+j,7×3600)≠1 (j=1,2,3,4,5,6) 既然此猜想对所有正整数不成立,是否对无穷大的或无穷多个正整数n成立呢?进而,笔者将上述猜想进行改进。 引理1设p,q,e∈N,e|p,e|q,则∀m,n∈N,有e|(mp+nq)。 命题1设p,q∈N+,0 (np+j,nq)=1 证明取n=qx,其中x是正整数,使得qx>N,令j=q-1,则必有(qxp+q-1,qxq)=1。 事实上,若: (qxp+q-1,qx+1)=e 则e|(qxp+q-1),e|qx+1,从而由引理1有: e|[q(qxp+q-1)-pqx+1] 即: e|q(q-1) 同理: e|[qx-1q(q-1)-qx+1] 即: e|qx 再由e|q(q-1),e|qx可得: e|[qx-2q(q-1)-qx] 即: e|qx-1 由归纳法可得e|q0,即e|1,故e=1。得证。 根据前述命题,∃j:0 f(xn)=nq(q>1) 由于n可充分大,故f(x)在(x0-δ,x0+δ)无上界,从而f(x)是(x0-δ,x0+δ)上的无界函数。 [1]华东师大数学系.数学分析[M].第4版. 北京:高等教育出版社,2010. [2]冯克勤.初等数论及其应用[M]. 北京:北京师范大学出版社, 2003. [3]潘承洞,潘承彪.初等数论[M].第3版.北京:北京大学出版社,2013. [编辑] 洪云飞 O174;O156 A 1673-1409(2013)25-0012-02 2013-06-13 宋述刚(1961-),男,教授,现主要从事函数论及数学史方面的教学与研究工作。