匹配追踪保幅地震AVF剖面及同频率剖面的构建
2013-11-05张繁昌李传辉
张繁昌,李传辉
(中国石油大学(华东)地球科学与技术学院,山东青岛 266580)
地震资料分频解释技术利用地震信号丰富的频率信息,减少了常规解释的不确定性,在薄储层及小尺度地质目标的识别中起到了重要作用。唐湘蓉等利用地震波的高频信息进行了薄砂体预测[1];胥德平等探讨了基于广义S变换分频技术的储层识别方法[2];张志让等将频谱成像技术应用于特殊地质体的储层预测[3]。此外,不同频率下的振幅响应(AVF)剖面还携带有储层物性信息,Haitao等根据Biot饱和流体孔隙介质地震波的传播理论,设计了具有不同岩石物性参数(孔隙度、含油气饱和度、渗透率等)的模型,并研究储层地震响应在低频、中频和高频的变化规律与机理[4];并参照AVO 类型的划分,将AVF类型划分为3类[5],为利用AVF 规律进行储层物性解释提供了理论指导。
目前地震资料处理中通常采用两种分频技术,一种是带通滤波分频,一种是利用Morlet小波变换的多分辨特性进行分频。由于Morlet小波变换具有优良的时频局部化性质,可以将地震信号分解为一系列具有中心频率的窄带信号,较好地实现不同尺度地震信号的分离,近年来被广泛应用于地震分频处理之中[6-9]。
虽然小波分频技术在地震资料处理中得到广泛应用,但是Morlet小波变换方法得到的AVF剖面从低频到高频存在同相轴树形分叉、上下漂移等现象,难以追踪某一同相轴的振幅随频率变化规律。此外,Morlet小波变换得到的同频率剖面存在调谐效应,产生平行同相轴等假象。
Mallatt等提出的匹配追踪方法[10-11]具有很多优势,由匹配追踪得到的地震信号瞬时谱聚焦性最高[12-13],具有比Morlet小波变换更高的时间或频率分辨率。地震信号经匹配追踪分解后,可表示为一系列时频原子的组合,所以由匹配追踪时频原子完全重构地震信号非常简单,但利用时频原子构建AVF剖面和给定频率的同频率剖面却是研究的难点。
1 方法原理
匹配追踪分解算法通过创建超完备时频原子库,根据信号自身的特点将信号在时频原子库中展开,以实现信号的自适应分解。
设地震信号为s(t),D为进行信号分解的超完备时频原子库,D中的每个时频原子gγ均满足有限支撑性质。匹配追踪算法通过一步步重复迭代,将信号s(t)垂直投影到D的时频原子上。经过匹配追踪分解后,地震信号表示为不同振幅、中心时间、主频和相位的时频原子的线性组合[10]:

其中,an,tn,fn,φn分别表示第n个时频原子的幅度、中心时间、主频和相位。将第n个时频原子用gγn(t)表示,即grn(t)=gr(t-tn,fn,φn),则(1)式表示为
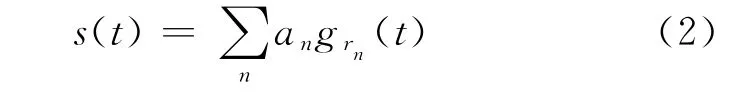
公式(2)说明地震信号经过匹配追踪分解后,就可以用一系列时频原子的线性组合来进行重构,但该式只能进行地震信号的完全重构,而不能重构给定频率的同频率信号。要利用时频原子构建同频率信号,需借助匹配追踪瞬时谱来实现。
目前,匹配追踪瞬时谱的计算普遍用各时频原子的Wigner-Ville分布表示[10,14],但这种表示方式只能提供地震信号的振幅分布。要利用匹配追踪时频原子构建同频率剖面,实现地震数据的分频处理,需要构建包含相位信息的瞬时谱形式,而不仅仅是振幅信息。
由于时频原子具有良好的有限支撑性质,其能量集中在以中心时间和主频为中心的时频点附近。设时频原子gγn(t)的频谱为Gγn(f),振幅包络为env[gγn(t)],将振幅包络在频率方向按照其频谱Gγn(f)加权,就得到该时频原子的瞬时谱
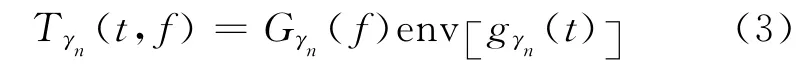
通过匹配追踪分解,地震信号被分解成一系列时频原子gγn(t),所有原子瞬时谱的叠加即为地震信号的匹配追踪瞬时谱:
回溯古时,有庄周不断扪心自问,在人生路途中寻觅到自己人生的意义。在他人都痛拍栏杆,嗟叹世道不公,意欲吞吐天地时,他却疑惑、思索。充耳为蜗角虚名,满目为勾心斗角,他毅然转身,洞察了超然物我之外的“蝴蝶”,发现了抟扶摇而上的“大鹏”,了悟了生死荣辱之外的至理。生而为庄周,他在一路探寻中摸索,在摸索中得到答案。《道德经》有言:“夫唯不争,故天下莫能与之争。”庄子以其“不争”之人生,活出了独特的风骨,发现了自己的人生意义。
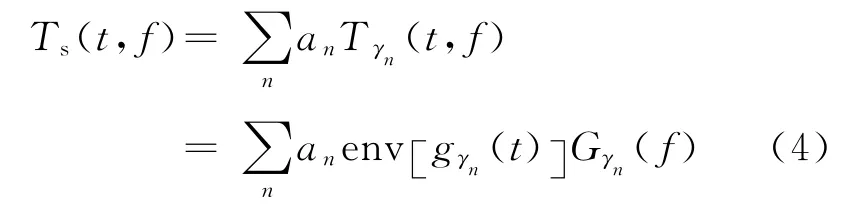
与Wigner-Ville分布计算匹配追踪瞬时谱的方法相比,(4)式表达的匹配追踪瞬时谱不但计算简洁,而且同时包含了振幅及相位信息。
同理,将所有时频原子gγn(t)的波形在频率方向按照Gγn(f)加权,即可以得到地震信号的AVF剖面:

该式反映了地震信号的振幅随频率变化规律。将(5)式沿频率方向积分,得:
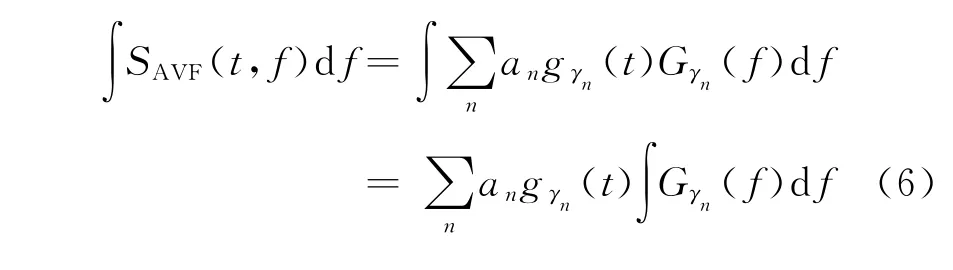
AVF剖面沿频率方向的积分应当为原地震信号,但比较(6)式和(2)式发现,二者并不相等,(6)式多了这一项,说明由(6)式重构的地震信号的振幅大小与原始地震信号并不相同,换句话说,(6)式不能实现地震信号的保幅重构。
为了实现地震信号的保幅重构,将(5)式改为

即在计算AVF 剖面时,首先对Gγn(f)进行归一化。这样,将(7)式对频率积分,得
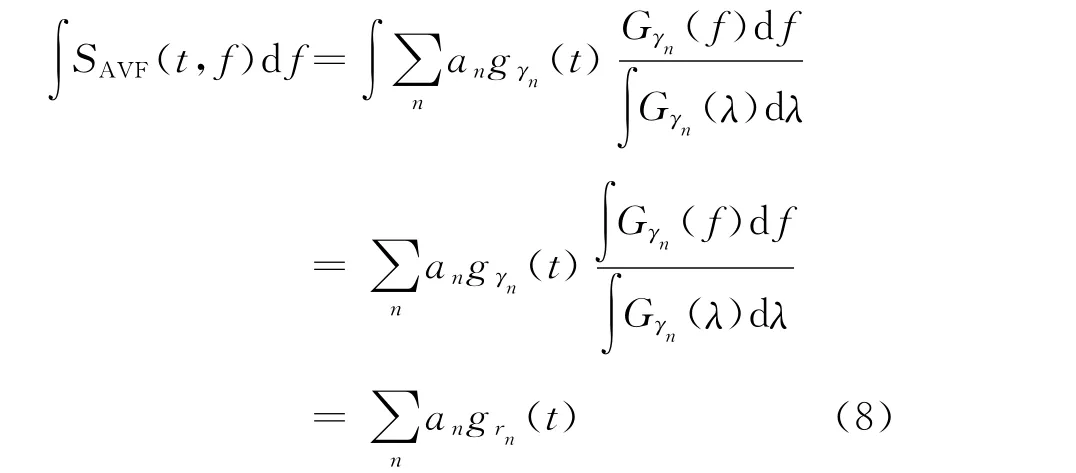
对比(8)式和(2)式,可见按照(8)式重构的信号就是原来的地震信号,实现了地震信号的保幅重构。
由(7)式得到振幅保持的地震AVF 剖面后,给定某一频率fj,就可以提取该频率的同频率信号DF(t,fj):

与(2)式不同的是,(9)式表示在重构过程中,虽然所有时频原子均参与计算,但每个时频原子被赋予不同的权重,其大小由频率fj位置处各自的频谱值决定。(9)式所表示的同频率信号构建方法由于包含了所有时频原子而使得频带较宽,同时,不同时频原子根据其位于fj频率处的谱值大小,对同频率信号的贡献有主次之分,使地震信号的主要能量集中在频率fj附近。地震剖面在匹配追踪分解后,每一道都按(9)式进行计算,就得到频率为fj时的同频率剖面。
2 方法测试
匹配追踪将地震信号分解成众多时频原子,各时频原子均有不同的主频、中心时间、振幅和相位,这些时频原子按照(2)式就可以完全重构原来的地震信号。那么,要利用匹配追踪结果对地震信号进行分频处理,即有选择地构建给定频率的信号,是否可以通过将此频率范围内的时频原子也按(2)式实现呢?根据这个设想,对图1a所示的实际地震剖面先进行匹配追踪分解,然后利用主频为30 Hz的时频原子构建了30 Hz同频率剖面(图1b)。分析发现,图1b的同频率剖面出现很多空白区,同相轴时连时断,不能很好地保持原地震剖面的地质特征,说明仅由给定频率的时频原子并不能合理地构建同频率剖面。
图1c为利用图1a地震剖面匹配追踪分解的时频原子按(9)式得到的30 Hz同频率剖面,通过与图1b的对比可见,由(9)式计算的同频率剖面不存在空白区,很好地保持了原地震剖面的特征。

图1 地震剖面及不同方法得到的30 Hz同频率剖面
3 结果对比
3.1 瞬时谱的对比
从图1a的地震剖面中任取一道地震信号,例如第10道,显示于图2a左侧,对其进行匹配追踪分解,然后利用(4)式计算此地震道的瞬时谱,其振幅分布如图2a右侧所示。为了对比,将该地震信号匹配追踪结果利用Wigner-Ville分布方法计算其振幅分布(图2b)。对比图2a和图2b可见,利用(4)式得到的瞬时谱,无论是在时频分辨率还是在能量聚集性上与Wigner-Ville分布方法的计算结果都几乎完全相同,说明了(4)式的正确性。
3.2 AVF剖面的对比
仍以图2a左侧的地震信号为例。利用(7)式计算得到该地震信号的AVF 剖面(图3a右侧)。图3b为同一地震信号利用Morlet小波变换得到的AVF剖面。由图3 可以看出,两种分频结果的主要能量分布一致,但是沿频率方向,图3b的AVF剖面表现出“树形分叉”现象,同相轴弯曲、分叉,难以追踪某一同相轴的振幅随频率变化规律;而在图3a中的匹配追踪AVF剖面上,同相轴平直,没有上下漂移现象,可以方便地进行AVF分析。
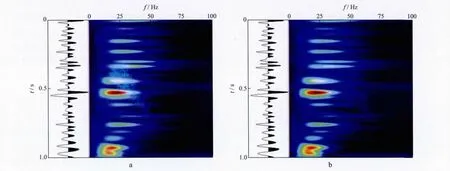
图2 不同方法得到的瞬时谱对比

图3 不同方法得到的AVF剖面对比
3.3 同频率剖面的对比
对图1a所示的地震剖面进行匹配追踪,利用(9)式的同频率信号构建方法对地震剖面逐道分频,得到每个地震道的AVF剖面,图4a为不同地震道的AVF剖面。经过匹配追踪分频处理后,得到三维频率数据体,再沿频率方向逐道取出特定频率的信号,便得到同频率剖面,图4b为不同频率的剖面排列在一起的三维显示。

图4 匹配追踪分频处理获得的三维频率数据体
图5为从图4b中取出的15,30和50 Hz的匹配追踪同频率剖面。为了对比,图6 给出了Morlet小波变换得到的对应频率剖面。可以看出,匹配追踪分频方法与Morlet小波变换一样具有多分辨率特性,能够分离出不同尺度的地震信号,利用不同频率的剖面可以揭示不同厚度、不同规模的地层反射特征。
进一步对比发现,图6所示的Morlet小波变换同频率剖面中存在平行同相轴假象,这是由于滤波造成的调谐效应。而在图5 的匹配追踪同频率剖面上则不存在这种调谐效应,不同频率的剖面很好地保持了图1a原地震剖面的反射特征。
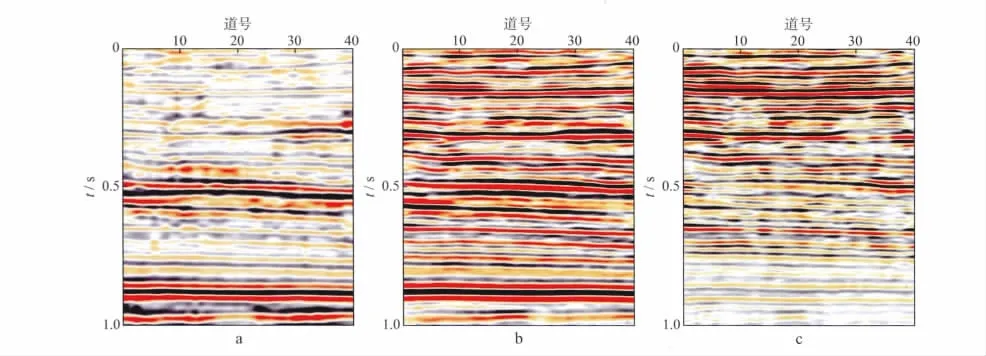
图5 匹配追踪同频率剖面
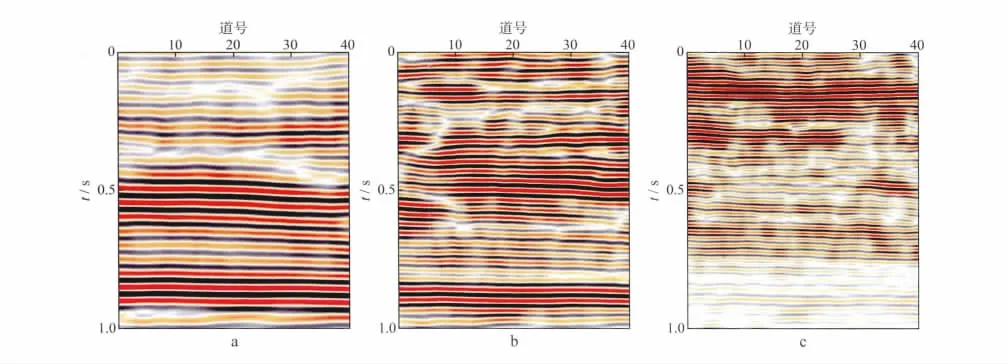
图6 Morlet小波变换同频率剖面
观察图5和图6还可以看出,15Hz低频剖面表现为浅层较弱、深层较强;而50 Hz高频剖面表现为深层较弱、浅层较强;只有30 Hz剖面深浅层反射能量比较均衡。这是由于地震波在地下传播过程中,高频成分衰减较快,而地震资料处理通常是依据地震波的优势频带进行,不能很好地兼顾高、低频成分。将图5a和图5c分别进行Q扫描[14-15]等处理,得到如图7所示的结果。可以看出,不同频率成分的剖面上,浅、中、深层能量都保持均衡。

图7 对图5数据进行剩余补偿后的同频率剖面
4 结束语
匹配追踪分解方法得到的瞬时谱具有极高的聚焦性,如何利用高聚焦性的时频原子构建AVF剖面及给定频率的剖面却是研究的难点。我们在匹配追踪算法的基础上,提出了一种保幅AVF剖面构建方法。该方法将所有时频原子在频率方向上按其归一化频谱加权,即可得到地震信号的AVF 剖面。同Morlet小波变换得到的AVF剖面相比,本方法得到的AVF 剖面上没有出现同相轴弯曲和分叉现象。
在取得AVF 剖面的基础上,进一步构建了匹配追踪同频率剖面,即利用匹配追踪时频原子对给定频率进行地震同频率信号的构建,构建过程中所有时频原子均参与计算,其贡献大小由该频率位置处各时频原子的谱值决定。利用该方法提取的同频率剖面,有效避免了以滤波机制为基础的分频方法造成的平行同相轴假象,分频效果更理想。由此解决了匹配追踪分频重构技术难题。
[1]唐湘蓉,蔡涵鹏,贺振华.地震波高频信息在薄层砂体预测中的应用[J].石油物探,2012,51(3):244-250 Tang X R,Cai H P,He Z H.Thin-bed sand body prediction based on seismic wave high-frequency information[J].Geophysical Prospecting for Petroleum,2012,51(3):244-250
[2]胥德平,郭科,文晓涛,等.基于广义S变换和JADE算法的储层识别[J].石油物探,2011,50(4):319-323 Xu D P,Guo K,Wen X T,et al.Reservoir identification based on GST and JADE algorithm[J].Geophysical Prospecting for Petroleum,2011,50(4):319-323
[3]张志让,杨建勋,李梅,等.频谱成像技术在特殊地质体储层预测中的应用研究[J].石油物探,2011,50(1):69-75 Zhang Z R,Yang J X,Li M,et al.Application of frequency spectrum imaging technique for reservoir prediction of special geological bodies[J].Geophysical Prospecting for Petroleum,2011,50(1):69-75
[4]Haitao R,Gennady G,Fred H.Amplitude versus frequency variations in thinly layered porous rocks[J].Expanded Abstracts of 78thAnnual Internat SEG Mtg,2008,1744-1748
[5]Haitao R,Gennady G,Fred H.Poroelastic analysis of amplitude-versus-frequency variations[J].Geophysics,2009,74(6):41-48
[6]Avijit C,David O.Frequency-time decomposition of seismic data using wavelet-based methods[J].Geophysics,1995,60(6):1906-1916
[7]龚洪林,王振卿,李录明,等.应用地震分频技术预测碳酸盐岩储层[J].地球物理学进展,2008,23(1):129-135 Gong H L,Wang Z Q,Li L M,et al.Predicting carbonate reservoir by applying seismic spectral decomposition technique[J].Progress in Geophysics,2008,23(1):129-135
[8]魏文,王小杰,李红梅.基于叠前道集小波域Q 值求取方法研究[J].石油物探,2011,50(4):355-360 Wei W,Wang X J,Li H M.Study on extraction method for Q based on pre-stack gather in wavelet domain[J].Geophysical Prospecting for Petroleum,2011,50(4):355-360
[9]Marcilio C M,Kurt J M,Paulo R S,et al.Wavelet transform Teager-Kaiser energy applied to a carbonate field in Brazil[J].The Leading Edge,2009,28(3):708-713
[10]Mallat S,Zhang Z.Matching pursuit with time-frequency dictionaries[J].IEEE transactions on signal processing,1993,41(12):3397-3415
[11]张繁昌,李传辉.基于正交时频原子的地震信号快速匹配追踪[J].地球物理学报,2012,55(1):277-283 Zhang F C,Li C H.Orthogonal time-frequency atom based fast matching pursuit for seismic signals[J].Chinese Journal of Geophysics(in Chinese),2012,55(1):277-283
[12]Castagna J P,Sun S J,Siegfried R W.Instantaneous spectral analysis:Detection of low-frequency shadows associated with hydrocarbons[J].The Leading Edge,2003,22(2):120-127
[13]李传辉,张繁昌.地震信号可变分辨率匹配追踪频谱成像方法[J].石油物探,2012,51(3):213-218 Li C H,Zhang F C.Variable resolution matching pursuit spectrum imaging of seismic signals[J].Geophysical Prospecting for Petroleum,2012,51(3):213-218
[14]Wang Y H.Seismic time-frequency spectral decomposition by matching pursuit[J].Geophysics,2007,72(1):13-20
[15]魏文,王兴谋,李红梅,等.基于地震波衰减的特征属性重构方法[J].石油物探,2012,51(3):219-225 Wei W,Wang X M,Li H M,et al.Method of characteristics attributes reconstruction based on seismic wave attenuation[J].Geophysical Prospecting for Petroleum,2012,51(3):219-225
