多子波分解与重构中子波的优选

黄 跃，许 多，文雪康

（1.中国石油化工股份有限公司多波地震技术重点实验室，四川德阳 618000；2.中国石油化工股份有限公司西南油气分公司，四川成都 610016；3.中国石油化工股份有限公司西南油气分公司勘探开发研究院德阳分院，四川德阳 618000；4.中国石油化工股份有限公司西南油气分公司监理中心，四川德阳 618000）

地震道多子波分解（简称多子波分解）就是将地震道分解为各种不同主频、不同宽度以及不同时间位置的子波。将这些子波简单叠加在一起即可精确地恢复原有的地震道。针对目标层位精细构造解释或油气藏特征描述的需要，可以有选择地对分解后的子波进行叠加，重构新的地震道，以突出相应的波场和波组特征。Castagna等［1］将多子波分解所获得的瞬时谱的低频阴影用于含气性检测取得了较好的效果；赵爽等［2］应用该方法进行含气性检测；王昕等［3］将该方法应用于储层预测。

目前多子波分解方法主要采用确定性子波进行地震道分解，人们对于子波的选择以及不同子波类型对地震重构信号分辨率、连续性等方面的影响尚不够重视。事实上，在实际地震资料的多子波分解与重构过程中，选择不同的子波能够突出不同的地震属性特征。以复数Paul子波和复数Morlet子波为例，理论上复数Paul子波具有更好的时间分辨率，适合处理信噪比高但相位变化快的信号；而复数Morlet子波具有更好的频率分辨率，时间分辨率相对较差，适合地震波吸收衰减研究。有鉴于此，根据不同的地质任务和研究目的合理进行子波选择无疑是十分必要的。我们从多子波分解常用的匹配追踪算法出发，通过理论计算和实际资料处理，对比分析Paul子波和Morlet子波对重构信号的分辨率及连续性等方面的影响，探讨子波选择的重要性，以期为多子波分解方法的应用，尤其是子波选取，提供指导和借鉴。

1 基本原理

地震道多子波分解中最常用的算法是匹配追踪算法，它通过迭代将地震道分解成一系列与其时频特征相匹配的子波［4－8］，是从一系列连续小波集合（子波字典）基函数中选取出与地震信号相匹配的一系列子波（也称为子波原子）的运算过程。在此过程中，每一次迭代均可获得一个最优的子波，经过N次迭代之后，地震道S（t）被分解为N个最优子波的代数和［9－14］，即

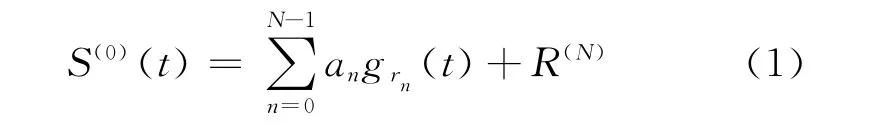
式中：an是第n个小波grn的振幅值；R（N）为残差；S（0）为初始地震道，R（0）＝S（0）。

对于每一个小波，可以用设定的4个参数γ＝｛u，σ，ω，φ｝来刻画，其中，u是时移，σ是时间轴尺度，ω是中心频率，φ是相移。具体匹配追踪过程如下。

1）对实际地震道进行Hilbert变换后，构建复地震道，将复地震道最大振幅包络处所对应的时间un当作时移，用其相应时刻的瞬时频率和瞬时相位作为中心频率ωn和相移φn。地震道经Hilbert变换后构建的解析信号为

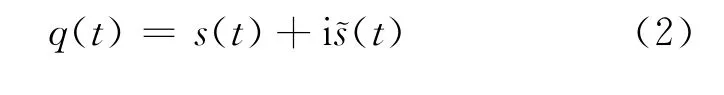
其振幅包络为

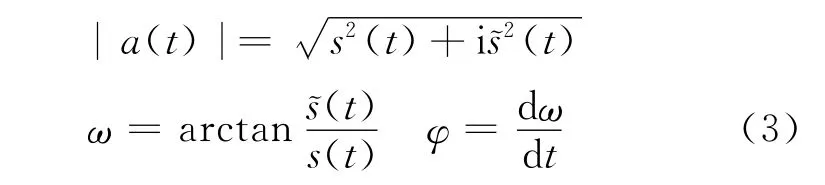
2）在相应的时间范围内利用

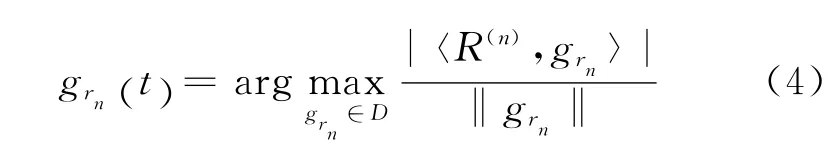
求取尺度控制参数σn。其中，D＝｛gr（t）｝γ∈Γ是一系列连续小波的集合（子波字典）；〈s，g〉表示函数s和g的内积；为子波grn的标准化。在参数un，ωn，φn确定后，在一定范围内选取σn进行扫描，当满足公式（4）最大值条件时停止，此时的σn就是最佳值。当｛u，σ，ω，φ｝确定后，对每一个参数给定一较小的扰动范围及固定的变化步长，再次利用公式（4）对其进行优化。

3）通过下式来估算最佳小波grn的振幅值：

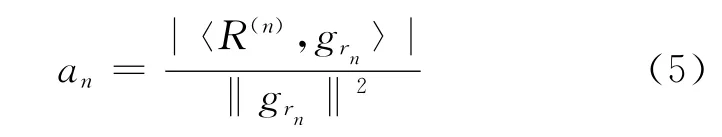
对于当前迭代分解和正交投影而言，R（n）＝angrn＋R（n＋1），其 中，grn与R（n＋1）是正交函数。选取使最大，即最小时的grn。在经过全部的N次迭代之后，最终所得的最小残差R（N）（t）被当作噪声。

由于复数Paul子波和复数Morlet子波的速度频散和振幅衰减属性与地震子波相似，因此，通常选择这两种子波来进行多子波分解与重构［1－3］。复数Paul子波和复数Morlet子波的表达式 为［1，8］

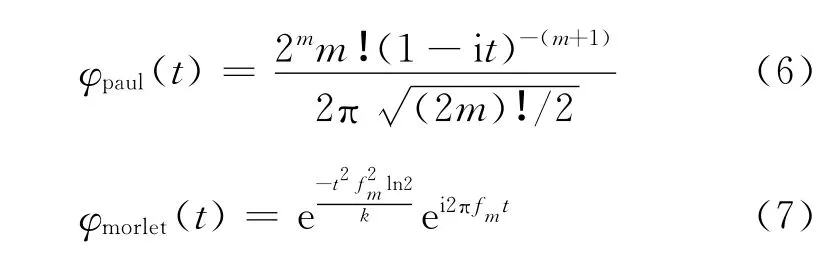
式中：m为控制Paul子波宽度的参数；k为控制Morlet子波宽度的参数；fm为主频。

在实际的匹配追踪算法中，复数Paul子波和复数Morlet子波的选择对算法本身无任何影响，但在迭代匹配的过程中，选择不同类型的子波对最终结果有一定影响——每次迭代分离出的子波在形状上稍有差异，因此，利用这些子波重构的剖面也有所不同。

2 不同子波分辨率差异性理论分析

为了说明不同子波类型对地震重构信号分辨率影响的差异性，我们利用公式（6）和公式（7），通过理论计算来分析复数Paul子波和复数Morlet子波对重构信号频率分辨率的影响。

所谓频率分辨率是指将两个相邻谱峰分开的能力。对单个子波而言，可以用子波谱的宽度来描述。复数Paul子波和复数Morlet子波的表达式中都有一个控制子波宽度的参数，子波的宽度与分辨率有关，宽度越小说明频率分辨率越高。

2.1 复数Paul子波

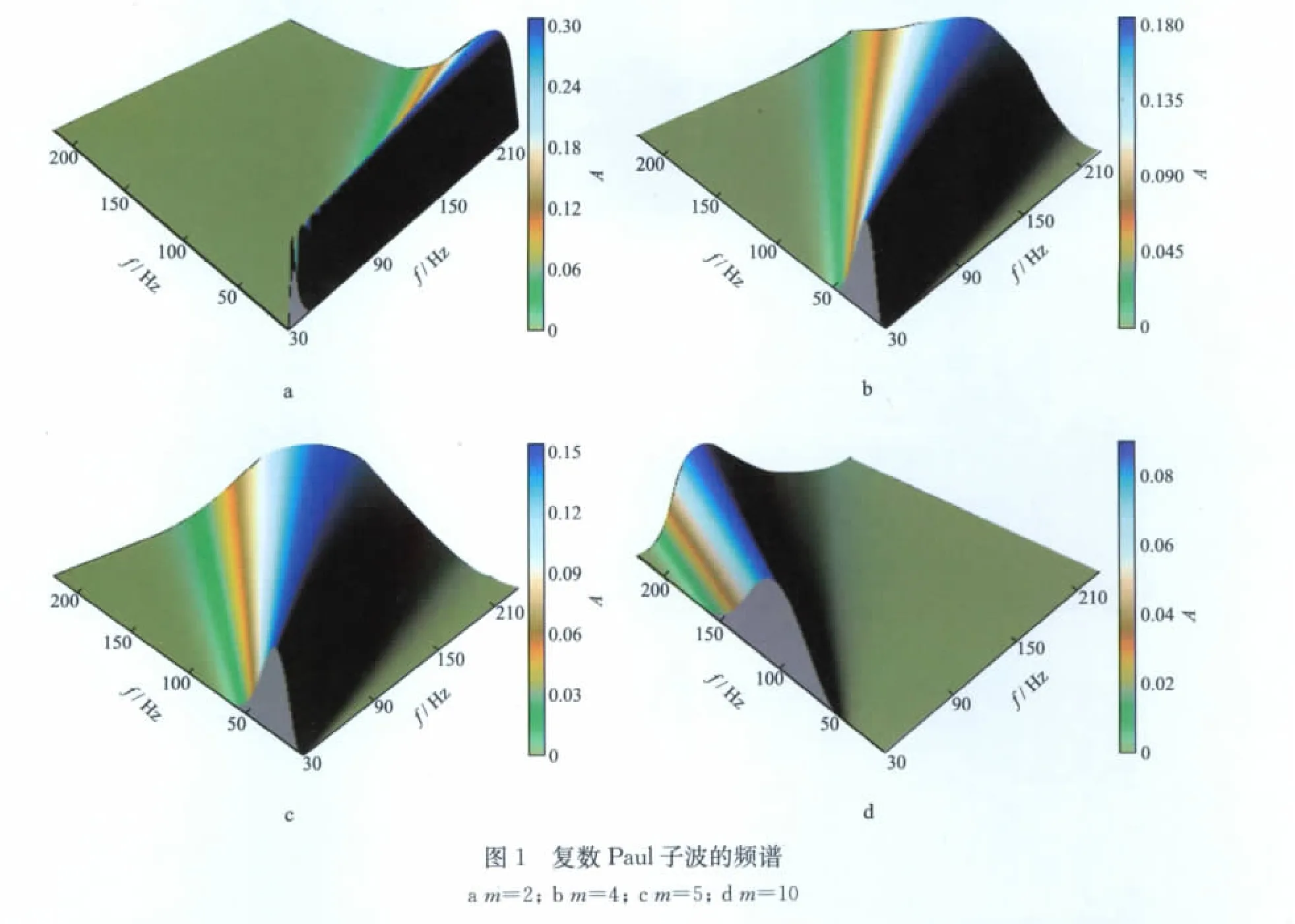
m为控制Paul子波频率分辨率的参数，因此，通过改变m值计算具有不同m值的Paul子波频谱，利用子波谱的宽度来讨论它的频率域分辨率。图1分别给出了m值分别为2，4，5，10四种情形下复数Paul子波的三维频谱。为便于子波频谱形态和宽度的对比分析，部分图的频率轴从30Hz开始显示。

从图1可见，当m较小时（图1a，m＝2），尽管Paul子波频谱在频率域的宽度相对较小，也就是说频率域分辨率相对较高，但因其频谱宽度很窄，在低频固定频率切片上接近一个脉冲形状。由公式（6）可知，m太小时，子波宽度几乎为零，不能形成完整的振幅谱曲线，因此，其三维频谱上显示不完整，有数据的缺失。当m较大时（图1c，图1d；m＝5，10），子波宽度很大，显示出较低的频率分辨率，且子波谱形状会发生畸变。特别是图1d中所显示的子波谱形状，与理想的光滑对称子波谱相去甚远，存在严重扭曲现象，若利用这种子波进行地震道多子波分解与重构，必将导致地震信号的严重失真。

通过m的改变可以看出，随着m的增加，子波从窄变化到宽，但m太大时子波形状会发生畸变。因此，在实际应用中，m值的选择必须适中。通过对m值的连续扫描分析，理论上我们认为，m＝4是Paul子波频率分辨率的最佳控制参数（图1b）。

2.2 复数Morlet子波

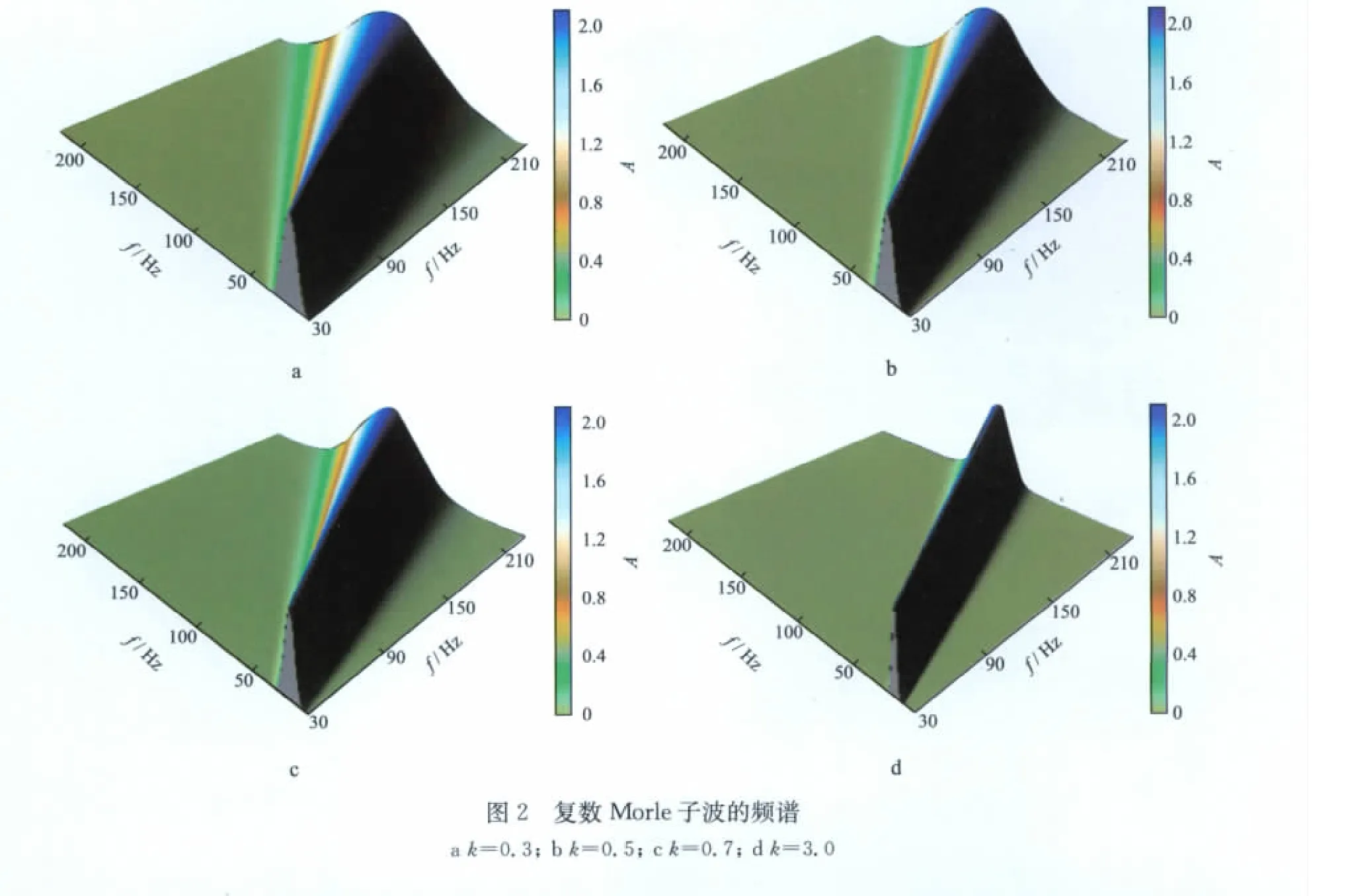
k为控制Morlet子波频率分辨率的参数，通过改变k值可以计算不同k值的Morlet子波频谱（图2）。

图2显示了k值分别为0.3，0.5，0.7和3.0时，复数Morlet子波的三维频谱。从图2可以看出，随着k值增大，子波的宽度越来越小，说明复数Morlet子波在频率域的分辨率越来越高，时间分辨率越来越低，用复数Morlet子波对地震信号分析时既要考虑频率分辨率也要考虑时间分辨率。通过对图2 进行对比分析，理论上我们认为，k＝0.5是Morlet子波频率分辨率的最佳控制参数。

3 实际应用效果对比分析

为了更好地揭示子波选择对地震道分解与重构的重要性，采用匹配追踪算法，选择复数Paul子波、复数Morlet子波分别对四川新场工区实测地震资料进行了多子波分解重构处理和对比分析。

图3为不同m值复数Paul子波分解所得主频为45～55 Hz的高频子波重构地震剖面（m＝2，4，5，10）。通过对比分析可知，当m＝2时，剖面连续性很好，低频成分明显，视觉上与子波主频不一致。其主要原因是m＝2时子波的低频能量缺失，导致最终结果低频能量明显增强。当m＝10时，重构剖面主频似乎很高，但信噪比极差，几乎看不到有效信号。m＝5时与m＝4重构信号有些相似，仅连续性较差。m＝4时，子波谱形状的对称性和完整性都很好，并且重构剖面也比较符合实际；m＝5时子波形状有一些扭变。通过综合分析认为，m＝4为最佳参数，这与理论分析的结果（图1）一致。

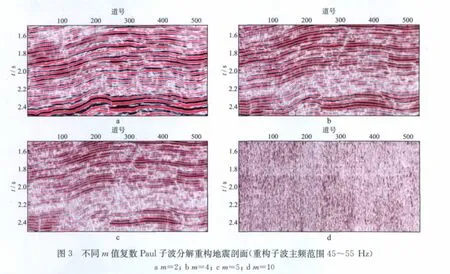
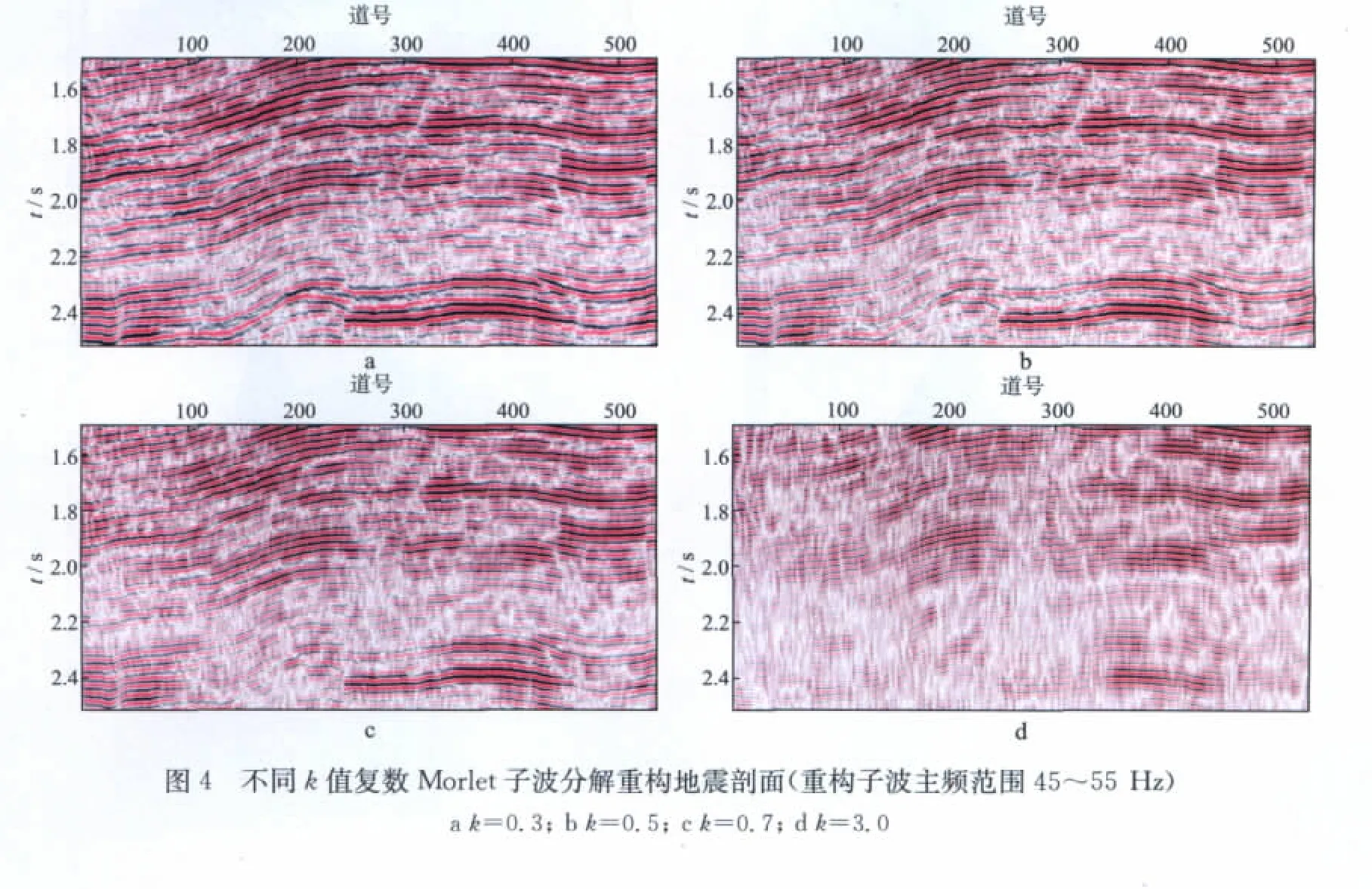
图4 给出了不同k值复数Morlet子波分解所得主频为45～55 Hz的高频子波重构地震剖面（k＝0.3，0.5，0.7，3.0）。对比可见，当k＝3.0时，由于重构子波频谱宽度很窄（图2d），导致重构地震信号的信噪比和连续性较差，一些强同相轴明显变弱（图4d）。而当k为0.7时，重构信号虽然在连续性上要好于k＝3.0，但与k＝0.5（图4b）相比仍然有信号失真现象（图4c）。当k＝0.3时（图4a），虽然重构信号的连续性和信噪比都要高于k＝0.5，但考虑到子波主频为45～55 Hz，有部分低频信号的缺失才是合理的，再对比复数Morlet子波频谱，分析认为k＝0.5 为复数Morlet子波的最佳分辨率参数。

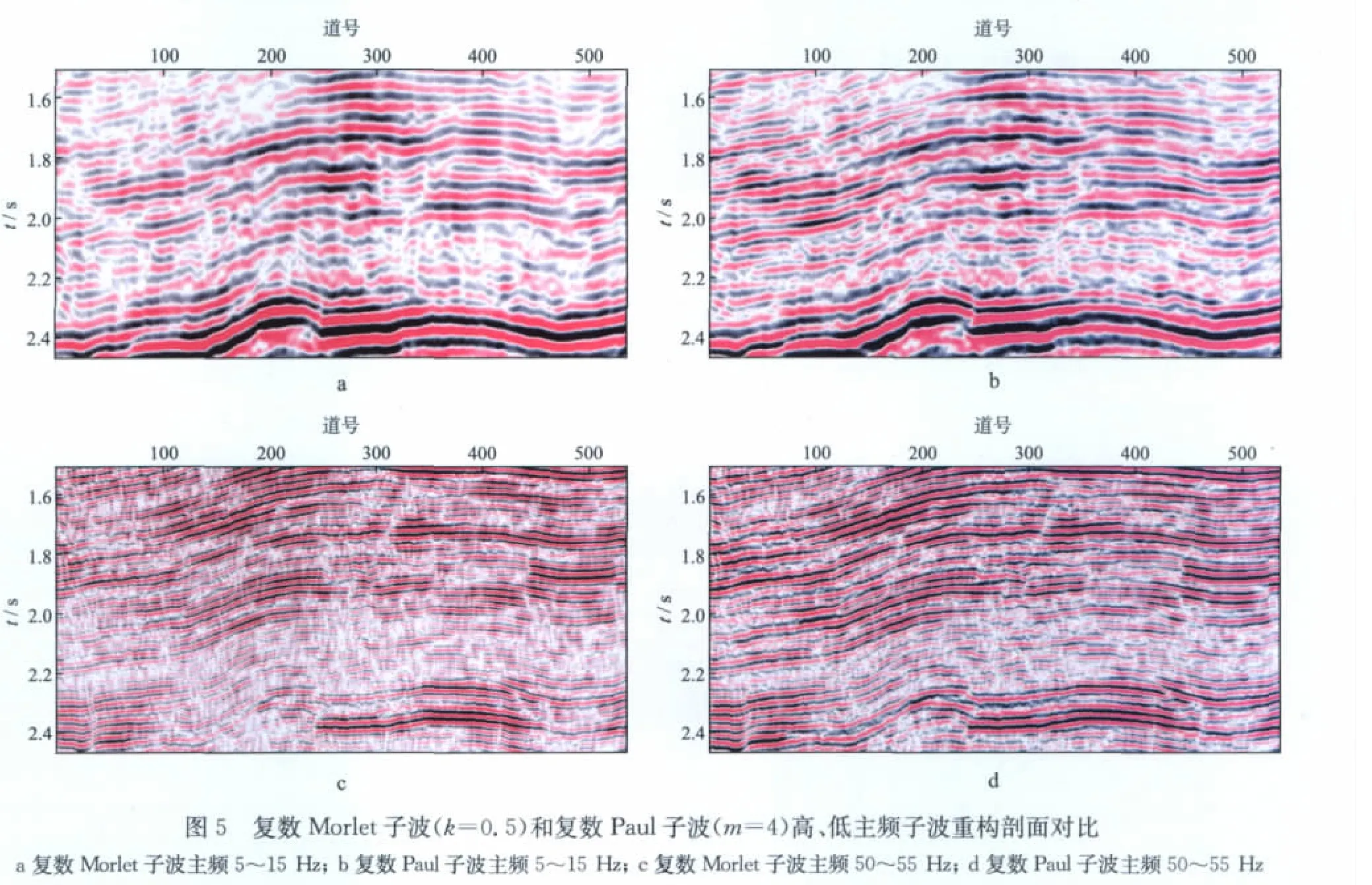
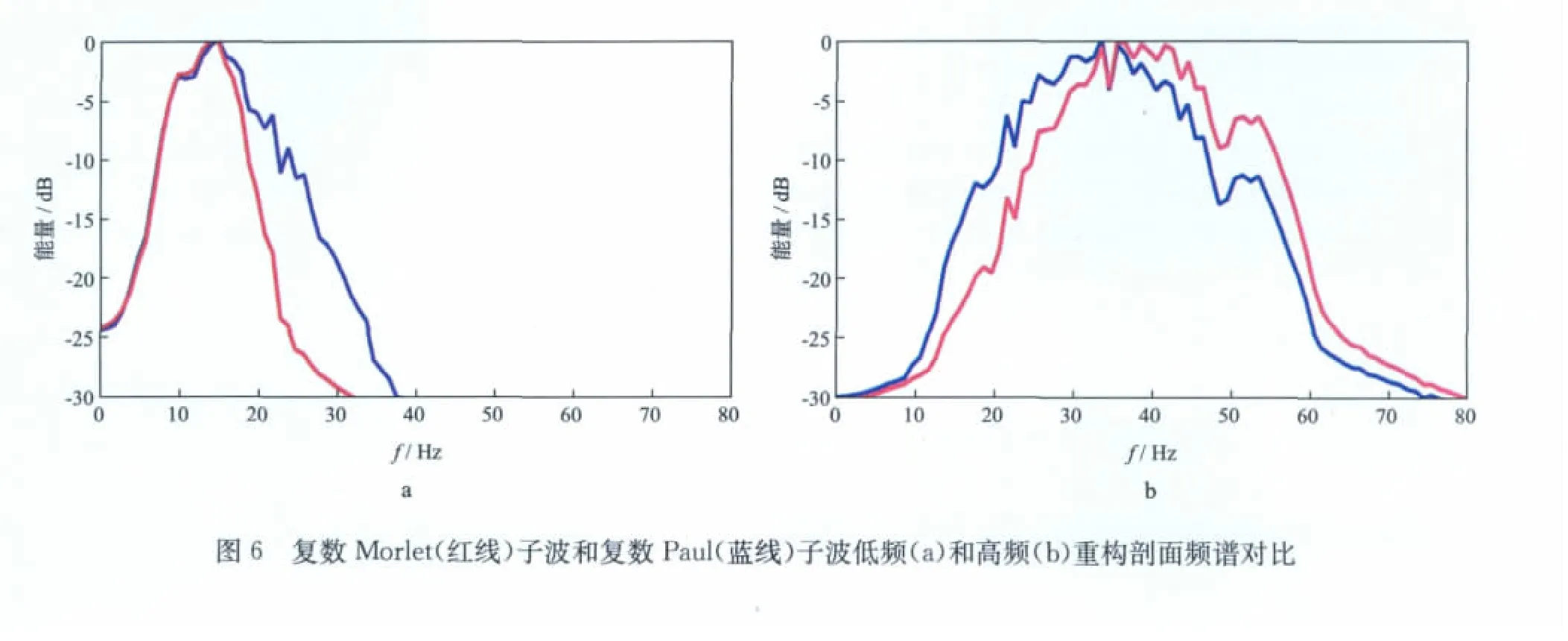
为了进一步对比分析基于复数Morlet子波（k＝0.5）和复数Paul子波（m＝4）分解重构结果的差异性，图5 和图6 分别给出了高、低频复数Morlet子波和复数Paul子波的重构剖面及其频谱。通过对比不难看出，复数Paul子波重构剖面的连续性和分辨率均优于复数Morlet子波重构剖面。低主频情形下复数Paul子波重构剖面包含了更多的高频信息（图6a）；高主频情形下复数Paul子波重构剖面具有相对较好的抗噪性。究其原因，可能是由于复数Paul子波重构对高频噪声的放大作用较弱所致（图6b）。

4 结论

通过理论和实际应用效果对比分析，得到如下认识：①m＝4是Paul子波最佳频率域分辨率控制参数，k＝0.5为Morlet子波最佳频率域分辨率控制参数；②复数Paul子波能使重构剖面保留更多的低频能量，同相轴更连续，构造更清晰，而复数Morlet子波高低频频谱差异大，重构剖面同相轴连续性相对较差。因此，基于复数Paul子波的重构剖面适合反射同相轴连续的地下构造研究，基于复数Morlet子波的重构剖面适合地震波吸收衰减研究。

［1］Castagna J P，Sun S J，Siegfried R W.Instantaneous spectral analysis：detection of low－frequency shadows associated with hydrocarbons［J］.The Leading Edge，2003，22（2）：120－127

［2］赵爽，李仲东，许红梅，等.多子波分解技术检测含煤砂岩储层［J］.天然气工业，2007，27（9）：44－47 Zhao S，Li Z D，Xu H M，et al.Using multiple wavelet decomposition technique to detect the sandstone reservoir with coal layer［J］.Natural Gas Industry，2007，27（9）：44－47

［3］王昕，魏刚，刘歆，等.多子波分解与重构技术在复杂储层预测中的应用［J］.断块油气田，2010，17（3）：289－292 Wang X，Wen G，Liu X，et al.Application of seismic trace－wavelet decomposition and reconfiguration technology in complex reservoir prediction［J］.Fault－Block Oil ＆Gas Field，2010，17（3）：289－292

［4］Partyka G，Gridley J，Lopez J.Interpretational applications of spectral decomposition in reservoir characterization［J］.The Leading Edge，1999，18（3）：353－360

［5］Liu J，Wu Y F，Han D H，et al.Time－frequency decomposition based on Ricker wavelet［J］.Expanded Abstracts of 74thAnnual Internat SEG Mtg，2004，1937－1940

［6］Liu J，Marfure K J.Matching pursuit decomposition using Morlet wavelets［J］.Expanded Abstracts of 75thAnnual Internat SEG Mtg，2005，786－789

［7］Wang Y.Multichannel matching pursuit for seismic trace decomposition［J］.Geophysics，2010，75（4）：61－66

［8］Wang Y.Seismic time－frequency spectral decomposition by matching pursuit［J］.Geophysics，2007，72（1）：V13－V20

［9］徐天吉，沈忠民，文雪康.多子波分解与重构技术应用研究［J］.成都理工 大 学学报，2010，37（6）：660－666 Xu T J，Shen Z M，Wen X K.Research and application of multi－wavelet decomposition and reconstructing technology［J］.Journal of Chengdu University of Technology，2010，37（6）：660－666

［10］陈发宇，杨长春.对依据频率的匹配追踪快速算法的改进［J］.石油物探，2009，48（1）：80－83 Chen F Y，Yang C C.An improvement for frequency－dominated fast matching pursuits algorithm［J］.Geophysical Prospecting for Petroleum，2009，48（1）：80－83

［11］陈发宇，杨长春.基于MP方法的地震信号快速分解算法［J］.地球物理学进展，2007，22（6）：1692－1697 Chen F Y，Yang C C.Seismic signal＇s decomposition based on matching pursuits method［J］.Progress in Geophysics，2007，22（6）：1692－1697

［12］马朋善，王继强，刘来祥，等.Morlet小波分频处理在提高地震资料分辨率中的应用［J］.石油物探，2007，46（3）：283－287 Ma P S，Wang J Q，Liu L X，et al.The application of frequency decomposition technique of morlet wavelet in enhancing seismic data resolution［J］.Geophysical Prospecting for Petroleum，2007，46（3）：283－287

［13］高静怀，吴茜，陈文超，等.小波变换域地震资料瞬时频率分析方法［J］.石油物探，2007，46（6）：534－540 Gao J K，Wu Q，Cheng W C，et al.Instantaneous frequency analysis of seismic data in wavelet transform domain［J］.Geophysical Prospecting for Petroleum，2007，46（6）：534－540

［14］邹问，陈爱萍，贺振华，等.基于S变换的地震相分析技术［J］.石油物探，2006，45（1）：48－51 Zhou W，Chen A P，He Z H，et al.Seismic faces analysis based on S transform［J］.Geophysical Prospecting for Petroleum，2006，45（1）：48－51