基于偏最小二乘回归密云森林蓄积量遥感估测

2013-11-05施鹏程彭道黎

江西农业大学学报 2013年4期

施鹏程，彭道黎

(北京林业大学林学院，北京100083)

森林是国家建设的重要资源，森林蓄积量是衡量一个国家森林健康与否的重要指标之一，同时森林蓄积量的消长动态还是林业经济效益的主要标志［1－2］。因此研究森林蓄积量的测定方法在林业系统中具有十分重要的意义。传统的森林蓄积量的调查方法主要通过森林资源一类和二类调查来获取信息，对标准地进行调查，以标准木平均胸径、树高进行估测，人为影响较大。除此，传统的调查方法劳动强度大，调查周期长，耗费大量的人力、物力和财力，而且不能及时反应森林的动态变化［3－4］。因此，为了及时掌握林业资源现状及动态变化，克服传统的森林蓄积量调查所存在的缺点，急需引进新方法和新技术进行森林资源调查。

近年来，随着高空间分辨率遥感技术的发展，GIS 和GPS 技术在森林资源调查和管理中的应用不断深入，国内外不少学者借助GIS、GPS 和RS 及其集成技术进行森林蓄积定量估测［5－8］。诸多研究结果表明，遥感影像灰度值及其经线性组合构成的植被指数与郁闭度和蓄积量等都有很好的相关关系［9－11］，可作为定量因子参与方程估测森林蓄积量。本研究基于偏最小二乘回归针对2006 年北京市密云县森林蓄积量进行遥感估测，得到密云县森林蓄积量遥感估测的最优模型并进行相关的精度评价，为今后进行森林资源的快速监测及其实时变化分析提供理论基础和重要的技术支持。

1 研究区概况

密云县位于北京市的东北部(E116°39'33″－117°30'25″，N40°13'7″ －40°47'57″)，属于燕山山脉与华北平原的交接地，主要以山地为主，土壤类型以褐土为主。密云县气候为温带季风性半干旱气候，具有四季分明、雨热同期、干湿冷暖变化骤烈的特征。无霜期一般在183 ～186 d，年平均气温10.9 ℃。该县平均降水量为660 mm，主要集中在6—8 月份，降雨强度大，侵蚀力强。密云县森林植被主要是针阔混交林森林植被地带，以人工林为主，常见的树种主要为油松(Pinus tabulaeformis)、刺槐(Robinia pseudoacacia)、杨树(Populus)、臭椿(Ailanthus altissima)、侧柏(Platycladus orientalis Franco)及经济林等［12－13］。

2 研究方法

2.1 数据获取及其预处理

调查数据为密云县2006 年森林资源一类调查101 个样地点。遥感影像(2006 年)覆盖研究区，综合考虑了时相、季相、云量及其与一类清查数据的匹配性，影像空间分辨率为30 m。

利用ERDAS 和ARCGIS 等软件，借助密云县行政边界、覆盖研究区的DEM 数据，对影像数据进行辐射校正、几何校正、波段组合和图像裁剪等预处理，校正误差控制在1 个像元以内。

考虑到遥感因子和GIS 因子之间量纲不同的影响，将所有样本数据进行中心标准化，统一量纲［4］，如式(1)所示，

2.2 偏最小二乘回归

偏最小二乘回归是一种新型的多元统计数据的分析方法，由Wola 和Albano 于1983 年首次提出，可以较好的解决自变量之间存在多重相关性的问题，集多元线性回归分析、典型相关分析和主成分分析于一体的分析方法。

记因变量为Y=(y1，y2，…，yq)，自变量为X =(x1，x2，…，xp)，设因变量Y 与自变量X 均有n 个观测值，由此构成了数据表Xn×p和Yn×q。其中:X 为自变量矩阵;Y 为因变量矩阵;n 为样本个数，p 为自变量个数，q 为因变量个数。通过成分提取的方法来达到有效建模的目的。该方法分别在自变量矩阵X和因变量矩阵Y 中提取成分t 和u，提取后的成分t 是x1，x2，...，xp的线性组合，而u 则是y1，y2，...，yq的线性组合。为了回归分析的需要，偏最小二乘回归在提取成分时加上了以下2 个目标［14］:(a)t 和u尽可能多地携带各自数据表中的变异信息;(b)t 和u 的相关程度能够达到最大。满足目标(a)则t 和u可以尽可能好地代表数据表X 和Y，达到目标(b)则自变量的成分t 对因变量的成分u 有很强的解释能力。在对X 和Y 进行一次成分提取后，分别实施X 对t 的回归和Y 对t 的回归。如果回归方程已经达到满意的精度，则停止计算;否则，将X 关于t 回归后的残差矩阵与Y 关于t 回归后的残差矩阵进行新一轮的成分提取。如此反复，直至满足交叉有效性原则规定的条件，最终确定提取潜变量成分的个数，建立偏最小二乘回归方程。

偏最小二乘回归计算过程在MATLAB 软件中进行实现。

3 结果与分析

3.1 特征变量的筛选

回归自变量的筛选是建立回归模型的关键之处。将总样本中异常点进行剔除，从中选取60 个样本作为建模样本，再抽取17 个样本进行模型的精度检验。计算各因子与蓄积量之间的相关性、信息量及方差扩大因子，除去与蓄积量相关性极低的部分因子，分析结果如表1 所示。可以看出，蓄积量与郁闭度呈极显著相关(P≤0.01)，与TM1 和TM2 呈显著相关(P≤0.05)，与其他因子的相关程度不高。可见遥感因子和GIS 因子对蓄积量的独立解释能力不强。除了海拔和坡度外其他因子的方差扩大因子均大于10，可见因子之间存在严重的多重相关性。如果自变量间存在多重共线性，回归系数对样本数据的微小变化将变得非常敏感，如果利用这些因子直接建模，会使模型稳定性变差，还会出现病态特征［15］。因此本文将采用偏最小二乘回归降低变量之间的相关性，建立森林蓄积量估测模型。

表1 入选变量的相关信息Tab.1 Information table about the selected variables

3.2 模型的构建

在MATLAB 里进行偏最小二乘回归计算，得到常量及各变量的系数。建模提取了3 个最佳成分个数，还原到原始变量的回归方程系数，方程为:

式(2)中，Y 表示森林蓄积量，单位:m3/hm2。

3.3 精度检验和适应性评价

根据实测的数据，可以得到蓄积量的均值，为44.49 m3/hm2(表2)，将未参与建模的17 个检验样本的数据代入估测模型，偏最小二乘回归估测均值为37.65 m3/hm2，两者的绝对误差为6.84 m3/hm2，(图2)其中，样地10 的偏差最大。偏最小二乘回归主要针对整体进行预估，对于单一样本的精度还有待提高。对基于偏最小二乘回归所建立的模型进行总体精度验证:精度=1 －［实测值－估测值］/实测值。得到林分蓄积量的估测精度为84.63%。

将蓄积量的实测值与模型估测值进行配对样本T 检验(表2)，可以看出，实测蓄积量与模型反演蓄积量的相关系数为0.555，P=0.021 ＜0.050，因此认为两者存在相关性。回归模型T 值双尾检验概率P=0.187 ＞0.05，故可认为两组数据之间不存在显著差异，表明偏最小二乘回归反演模型具有较强的适用性，可用于估测密云县森林蓄积量。

表2 模型配对样本T 检验Tab.2 The paired samples T-test of the model

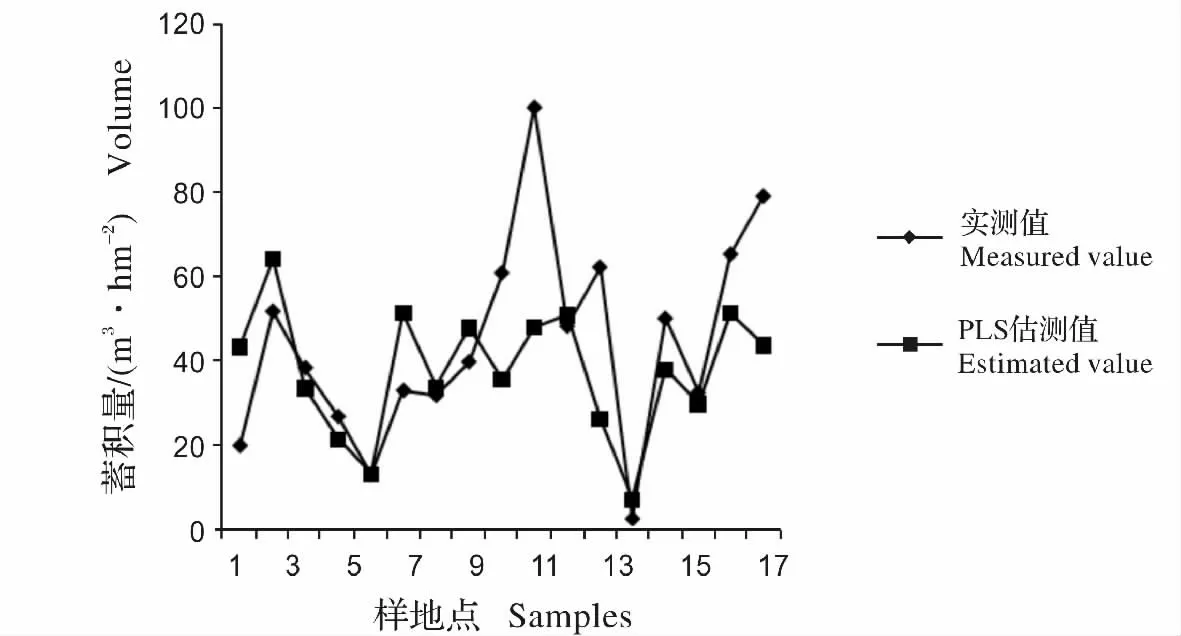
图1 蓄积量模型估算值与实测值拟合图Fig.1 The fitting figure of the estimated values and measured values

4 结论与讨论

遥感数据能提供动态的、综合的植被覆盖信息，它与系统的全国森林资源清查数据相结合丰富了森林资源经营管理的手段，并极大提高了工作效率［17］。本研究基于前人的研究，选取了与森林蓄积量关系较为密切的因子作为自变量，通过运用偏最小二乘回归得到森林蓄积量遥感估测模型。结果表明，该模型的稳健性、适用性均优于一般回归模型，尤其是可以在确保精度的同时克服因子之间的相关性。

(1)优选了16 个遥感因子和地形因子，利用偏最小二乘回归构建蓄积量模型，模型为:Y= －11.880 +85.701 郁闭度－172.850TM1 －97.335TM2 +116.709TM3 +23.468TM4 －65.685TM5 +78.104TM7 －9.825NDVI +0.351RVI －0.630TM7/TM3 +2.778TM4/TM2 －6.656TM437 +4.176TM452 +0.008 海拔+0.309 坡度。

(2)经配对样本T 检验，偏最小二乘回归估测精度为84.63%，实测蓄积量与模型反演蓄积量的相关系数为0.555，两者存在相关性(P ＜0.050)。该精度基本满足预测森林蓄积量模型的要求，因此，可以用少量的样地资料进行遥感蓄积估测代替森林资源一类调查。

［1］孙海鹏，包占青，姜志强.林木蓄积量预测［J］.内蒙古林业调查设计，1999，3:106 －109.

［2］程武学，杨存建，周介铭，等.森林蓄积量遥感定量估测研究综述［J］.安徽农业科学，2009，37(16):1 －2.

［3］李崇贵，赵宪文，李春干，等.森林蓄积量遥感估测理论与实现［M］.北京:科学出版社，2006.

［4］琚存勇，蔡体久.用泛化改进的BP 神经网络估测森林蓄积量［J］.林业科学，2006，51(12):59 －62.

［5］陈楚，关泽群，张鹏林，等.利用RS 和G1S 的森林蓄积量偏最小二乘估测研究［J］.湖北林业科技，2004，(4):5 －28.

［6］黄平，杨燕琼，侯长谋.基于RS、G1S 的杉木林分蓄积量判读模型研究［J］.中南林业调查规划，2003，22(1):25 －27.

［7］李春干，谭必增.历史调查数据参与森林调查因子遥感定量估测的研究［J］.林业资源管理，2003，31(1):58 －61.

［8］袁凯先，陈玉山，包盈智，等.森林蓄积量的遥感估测［J］.林业资源管理，1996，24(3):13 －17.

［9］丛沛桐，祖元刚，王瑞兰，等.GIS 与ANN 整合技术在森林资源蓄积量预测中的应用［J］.地理科学，2004，24(5):591－596.

［10］杨燕琼，吴奕敏，黄平，等.基于RS、GIS 的林分蓄积量估测［J］.华南农业大学学报:自然科学版，2003，24(3):73－77.

［11］刘志华，常禹，陈宏伟.基于遥感、地理信息系统和人工神经网络的呼中林区森林蓄积量估测［J］. 应用生态学报，2008，19(9):1891 －1896.