基于灰色理论的草郊公路桥线形控制

李宏平，汪 鼎

（1.湖北省恩施州建始县地方海事处，建始 445300；2.武汉理工大学道路桥梁与结构工程湖北省重点实验室，武汉 430070）

近些年来，预应力连续刚构桥相对于其他结构桥梁具有变形小、抗震性能好、造价低、行车舒适、美观且施工方便、快捷的优点，因此受到大跨径桥梁设计者的青睐［1］。悬臂施工法是连续刚构桥主要采用的施工方法之一。在悬臂施工过程中桥梁的整体线形会受到材料性能，截面特性，施工荷载和预应力损失，混凝土收缩徐变以及温度等诸多因素的影响［2］。而一座桥梁的成桥线形能否与设计线形尽可能的一致，达到设计规范的要求，对于成桥通车安全起着至关重要的作用。所以对连续刚构桥的线形监控就显得非常的重要了。该文以湖北省引江济汉通航工程中草郊公路桥的线形控制为例，运用灰色预测理论对施工阶段挂篮变形量进行预测，再将预测数据与实测数据进行比较分析，说明了灰色预测理论能够应用于实际施工过程中且具有较高的精度。

1 灰色理论预测模型

在桥梁线形监控过程中，我们监控的目的就是通过现有的数据来预测后续阶段的施工办法并且及时做出调整，以保证桥梁能够正常合拢和成桥线形符合设计要求，灰色理论的特点就是以目前所得到的少量信息为基础，并对这些基础信息数据加以加工和处理，建立灰色模型来预测系统未来的发展变化［3］。灰色系统理论就是利用离散函数序列建立近似的微分方程模型，该模型称之为GM模型，GM（1，1）模型为其中的一种，GM（1，1）模型对样本数目要求较低，所以我们选用GM（1，1）模型来作为线形控制的数学模型。GM（1，1）模型体系［4］建立如下“X（0）＝（X（0）（1），X（0）（2），X（0）（3），.…，X（0）（n））为GM（1，1）模型的原始数列，经过一次累加生成数列

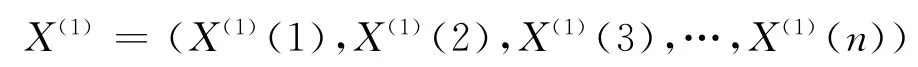
经过累加后，原始数列的规律性增强，为建立动态模型提供了重要的中间信息。

令Z（1）为X（1）的均值数列，即

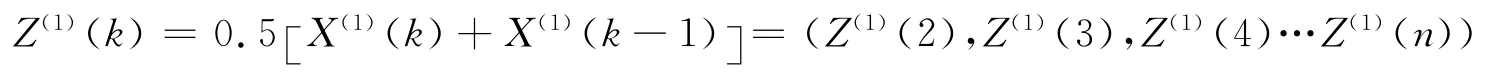
可建立GM（1，1）模型的灰微分方程为

其中，a，b为未知参数，分别称为发展系数和灰色作用量；X（0）（k）为灰导数；Z（1）（k）为白话背景值，对应的白化微分方程

X（0）（1）＝X（1）（1）可以解出白化响应式为

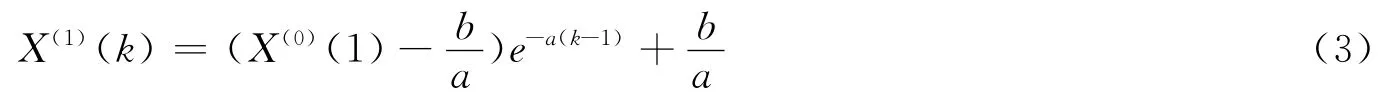
对于上述式子，根据最小二乘法，可以解出参数向量

其中

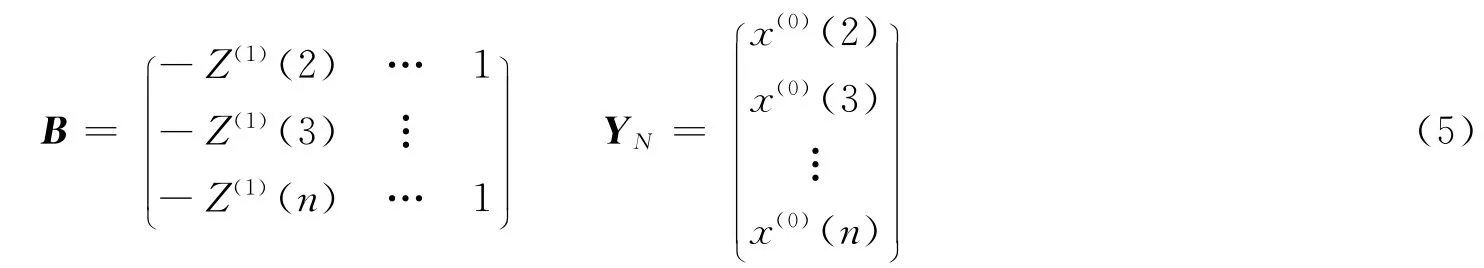
由式（4）求出a，b后，代入到白化响应式中，便可以求得数据X（1）（k＋1），将得到的数列再累加还原生成，可以得到X（0）（k＋1）。

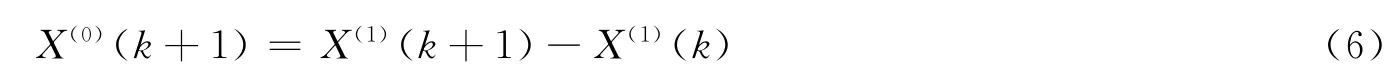
2 灰色理论在草郊公路桥线形控制中的应用

2.1 工程概述

引江济汉通航工程草郊公路桥桩号为K1＋687到K2＋313，为主跨80m 预应力混凝土一联三跨变截面箱梁，全桥长170m。跨径分别为45＋80＋45m。箱梁采用单箱单室箱型截面，箱梁顶板宽12m，底宽6m，顶板悬臂长度3 m，悬臂板端厚20cm，根部厚70cm。箱梁顶设2%的双向横坡。箱梁根部高度4.8m，跨中高度2.3m，箱梁根部底板厚60cm，跨中底板厚28cm。箱梁高度及底板厚度按2.0次抛物线变化。箱梁腹板根部厚80cm，跨中厚50cm，箱梁腹板厚度在腹板变化段按直线段渐变。挂篮悬臂施工，箱梁与主墩10＃墩，11＃墩形成2个T 构。桥梁示意图如图1所示。

2.2 挂篮变形预测

由于篇幅限制，所以该文以11＃墩小里程8＃块施工完毕后的各个工况浇筑前后，张拉前后的实测值与理论值之差作为原始数列建立模型（以10＃墩到11＃墩方向为大里程方向），相关数据如表1所示。

以实测值与理论计算值之差为原始数列建立模型，浇筑前后预测过程如下（单位：mm）：X（0）＝（－1.147，－1.346，－1.397，－1.278），建立GM（1，1）模型。

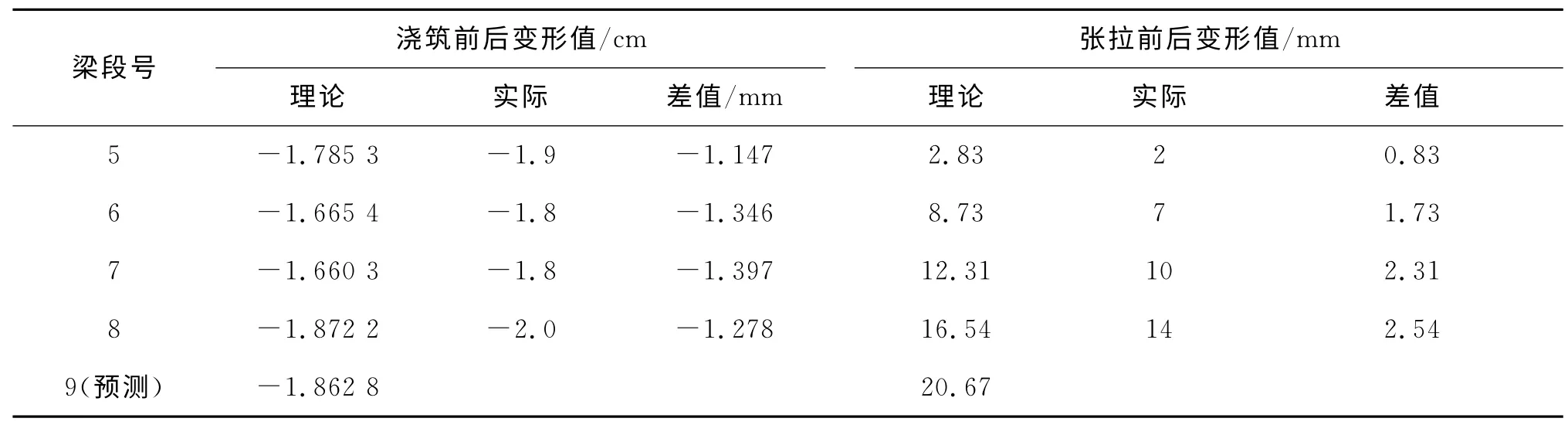
表1 11＃墩小里程8＃块施工完毕后的理论数据与实测数据

作AGO 累加生成数列X（1）＝（－1.147，－2.493，－3.89，－5.168），从而可以得出

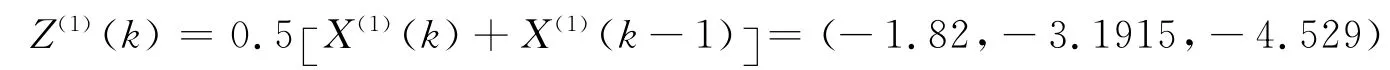
确定B，YN

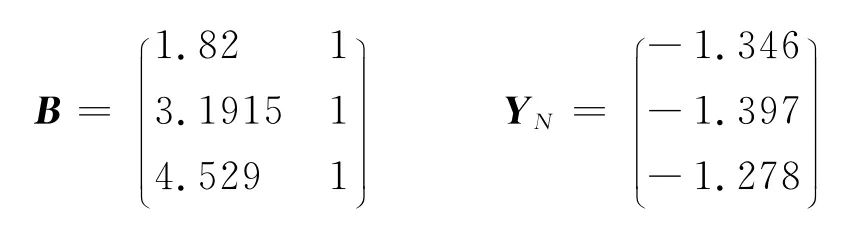
通过matlab编程计算，

可以得出

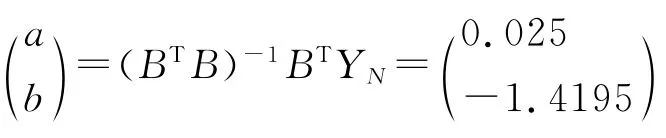
将a，b代入式（3）得出

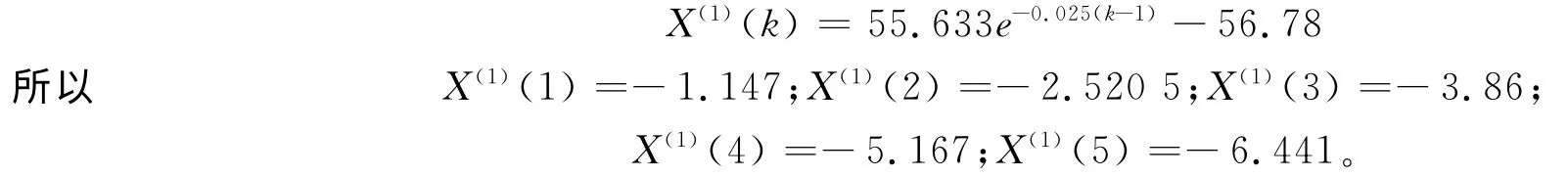
数据还原，累积递减可求出

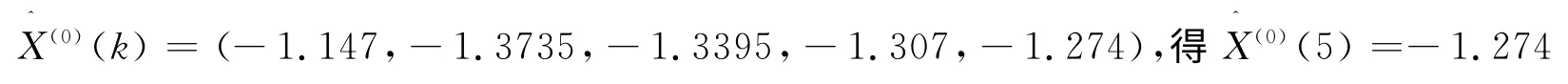
9＃块浇筑前后理论变形值为1.863cm，则9＃块浇筑后挂篮变形值预测值为：1.863＋0.1274＝1.990 4 cm，实测值为2.0cm。同理，张拉前后预测值（单位：mm），以理论计算值与实测值之差为原始数列建立模型。X（0）＝（0.83，1.73，2.31，2.54），建立GM（1，1）模型，经过一次累加可得：

X（1）＝（0.83，2.56，4.87，7.41），从而可以得出Z（1）（k）＝（1.695，3.715，6.14），将上述数据代入式（2），式（3），可以得出a＝－0.179 3，b＝1.502 8，将a，b代入式（3），当k＝1，2，3，4，…时，可以求出X（1）（k）＝（0.83，2.639，4.803，7.3925，10.4896）。

累积递减还原可得：＾X（0）（k）＝（0.83，1.809，2.164，2.589 5，3.097 1），可以得到＾X（0）（5）＝3.097 1，9＃块张拉前后理论变形值为20.67mm，则9＃块张拉前后挂篮变形值预测值为20.67－3.0971＝17.572 9 mm，实测值为17mm。

2.3 模型精度检验

在这里主要运用相对误差检验法进行精度检验［5］，其方法如下：

设按GM（1，1）建模法已经计算出X（1），并将X（1）作一次累减转化为

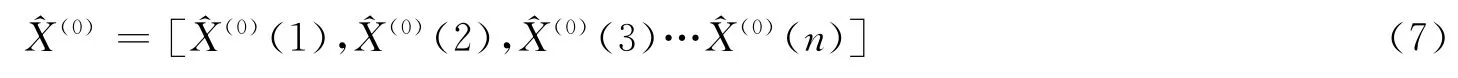
计算残差，可以得出

其中e（k）＝X（0）（k）－＾X（0）（k），k＝1，2，3…n计算相对误差得到

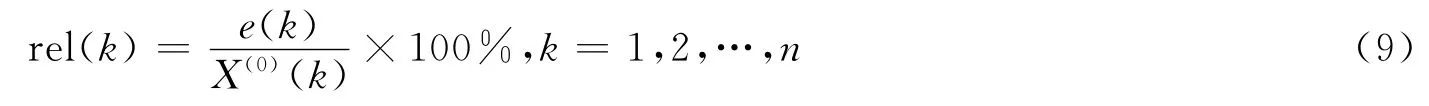
模型精度检验结果如下

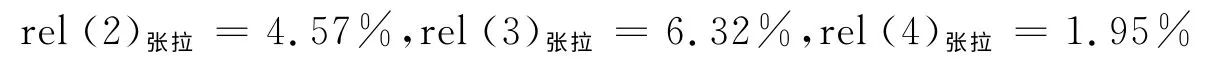
误差百分数均在8%以内，灰色模型与实际值比较吻合，可以用来预测。

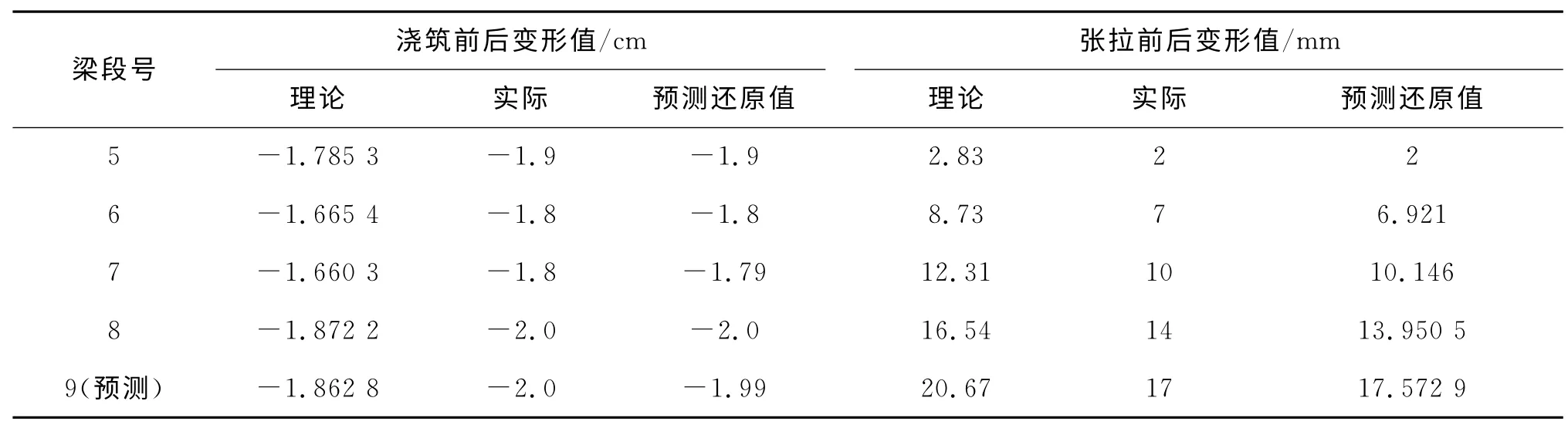
表2 11＃墩小里程8＃块施工完毕后理论值、实测值、预测值

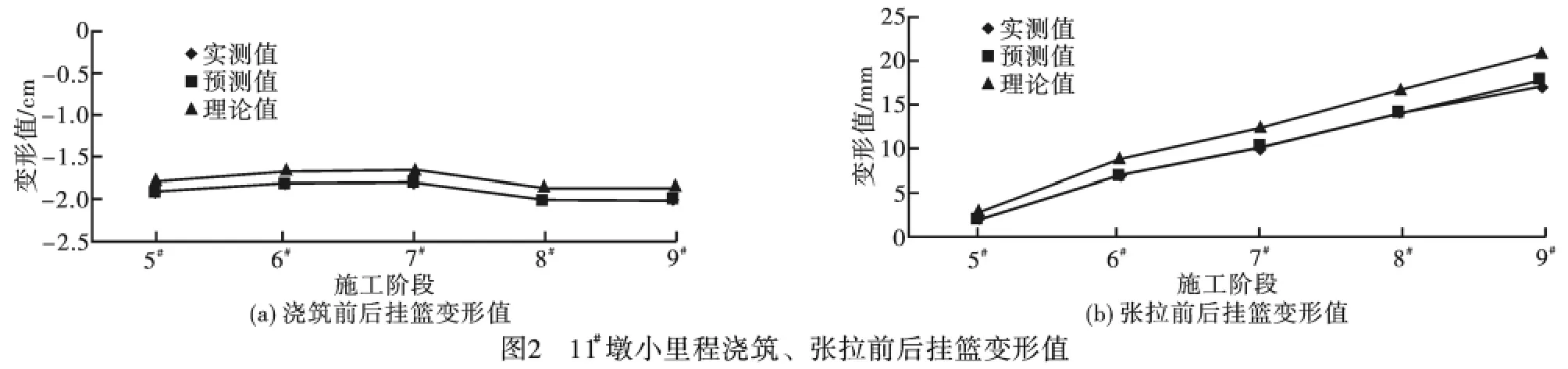
从图2中可以得出各工况挂篮变形预测值与实测值进行比较非常接近，最大误差在1mm 以内，误差相对来讲是非常小的，所以满足国际规范线形控制要求，充分说明了灰色预测理论在连续刚构桥施工线形监控中的应用可行性。

3 结语

经过灰色系统预测理论预测之后，11＃墩小里程测（中跨）的合拢段两侧高差为2mm，完全达到了施工监控的目的。以灰色系统理论建立GM（1，1）模型，对桥梁最后一个阶段浇筑后、张拉后的变形量进行预测，预测结果与实测结果比较接近，可以反映桥梁的施工过程，达到了线形控制的目的。表明：灰色预测理论能够运用于桥梁施工监控中且具有较高的精度。

［1］徐君兰.大跨度桥梁施工控制［M］.北京：人民交通出版社，2000.

［2］葛耀君.分段施工桥梁分析与控制［M］.北京：人民交通出版社，2003.

［3］邓聚龙.灰色系统理论教程［M］.武汉：华中理工大学出版社，1990.

［4］毕效辉，张海东.基于GM（1，1）模型的趋势预测方法及其应用［J］.西南科技大学学报，2003，18（4）：1－4.

［5］汪娟娟.灰色系统理论在大跨径桥梁施工控制中的应用［D］.武汉理工大学，2006.