网络控制系统二维优先级和带宽调度策略研究
2013-11-04张海艳陈其工魏利胜
张海艳,陈其工,魏利胜,江 明
(1.安徽工程大学,安徽 芜湖 241000;2.安徽检测技术与节能装置省级实验室,安徽 芜湖 241000)
引言
随着信息技术的蓬勃发展,传统的点对点控制系统正逐渐被网络控制系统(Networked Control Systems,NCSs)取代。网络化控制系统因其具有布线少、易于扩展和维护、低成本、信息资源共享、高效率和高灵活性等优点[1]被广泛应用于远程控制、国防和航天航空、复杂过程控制和智能交通等领域[2-3]。但是,由于网络的引入给网络控制系统的设计和研究均带来了挑战,网络控制系统中各控制回路的控制性能不仅取决于控制策略的使用,而且也依赖于网络数据的调度算法。特别是在网络带宽资源受限的情况下,合理的网络调度方法对改善系统的整体性能具有重要意义。
目前对于NCSs的研究,主要集中在控制策略、调度算法及控制和调度相结合等方面。褚红燕等[4]提出了包含丢包、时延信息以及量化信息的非线性网络控制系统(NNCS)T-S模糊模型,并采用Lyapunov方法和并行分布式补偿(PDC)方法分析了系统的稳定性。刘念等[5]将模糊控制理论引入反馈调度结构体系中,给出一种基于动态调节优先级和网络带宽分配的集成模糊反馈调度算法,通过在线调整各控制回路的优先级和采样周期,提高了网络控制系统的鲁棒性,同时也使得网络具备较高的服务质量。李祖欣等[6]针对一类通信约束的NCS,设计出一类集成控制和调度的资源约束系统模型,并用一种递增优化序列算法来求解优化的调度策略及其相应的渐近稳定及r指数稳定的H∞控制器。
因此,本文将在现有文献的研究基础上,尝试在调度器的设计过程中,提出一种基于二维优先级和带宽的NCSs反馈调度策略,以根据用户需求实时动态调整网络带宽和优先级,实现网络资源的有效配置,从而改善网络环境,克服了现有调度策略的不足。
1 体系结构
目前,许多网络调度算法的设计基本上都只考虑了优先级和带宽两者中的一项,甚少放在一起综合研究。考虑到现有的优先级调度算法基本上都是一维的,也即NCSs中所有任务的优先级都是在一维线性空间中进行调整,因此其调度策略基本上是由系统自身决定的,用户不能按照自己的需要随意的选择调度方法,这样就很难满足各种任务模型的需求。鉴于此,本文提出一种二维的优先级调度机制,在该机制中用户可以根据需要随意地选择系统中实现的调度策略。该优先级调度的思想是:设NCSs使用两级优先级,将各种典型的调度算法如RM、EDF、DM等作为系统的一级优先级,并且按照系统实际情况将各种算法进行排序(如设EDF的优先级最高,RM其次,DM最低等);然后将各个调度算法自身为任务分配的优先级划定为二级优先级;这样一级优先级和调度算法自身规定的任务优先级就共同决定了系统任务的执行次序。
但是,当高优先级的等候队列中始终有任务时,低优先级的任务可能将一直得不到执行,为此,本文在上述的优先级调度机制中加入了网络带宽资源的分配策略。这样由于受到带宽的限制,当分配给高优先级任务的带宽用尽时,它就不得不将网络的使用权让给较低优先级的任务,使低优先级的任务得到调度[7]。为与优先级调度算法的维数相对应,所提出的带宽分配策略同样设计成二维,其中一级带宽的分配主要是借助于NCSs中带宽与采样周期之间的关系,通过调整控制系统中各控制回路的采样周期间接实现对带宽的调整;二级带宽是受一级带宽分配结果的限制,二级带宽是在一级带宽分配的基础上根据任务的紧急程度按比例分配。二维优先级和带宽调度策略的体系结构如图1所示。由图可见,采用此调度策略以后,NCSs中有限的网络资源可以得到物尽其用,同时优先级的设置机制也充分满足了用户的需求,若所选用的调度策略的带宽分配得当的话,系统不仅能提供一定的硬实时能力,而且还能为其他的信息提供较高的服务质量。
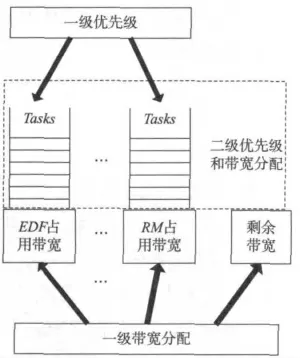
图1 二维优先级和带宽调度策略体系结构
2 二维调度策略的实现和分析
2.1 二维优先级算法描述
假设各控制回路的任务集为{T1,…,Tn},并令Ti,Tj为等候队列中截止期最短的两个任务,截止期分别为Di,Dj,且Dj≥Di。则一级优先级分配规则如图2所示。
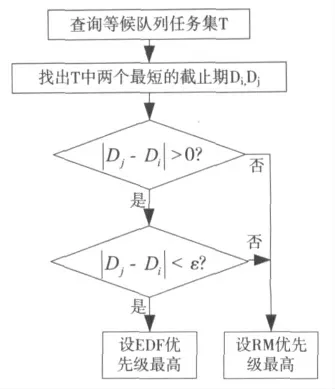
图2 一级优先级分配
当Dj=Di时,设RM调度算法的优先级高于EDF调度算法的优先级。图中的ε为阈值,代表了任务的紧急程度,要根据具体的系统进行确定。当ε=0时,一级优先级分配为RM调度算法高于EDF调度算法;而当ε足够大时,一级优先级分配为EDF调度算法高于RM调度算法。
二级优先级的分配取决于所采用的一级优先级的调度算法,如采用RM调度算法的任务优先级取决于采样周期,采样周期越小,优先级越高;采用EDF调度算法的任务优先级取决于截止期,截止期越短,优先级就越高。
2.2 二维带宽资源分配
假设在NCSs中,各控制回路中传感器到控制器和控制器到执行器的传输时间与控制器的计算时间之和为ei,各回路的采样周期为hi,网络带宽为bi。由文献[8]可知采样周期hi和网络带宽bi满足的关系为:

由式(1)可知,在ei确定的情况下为各控制回路所分配的带宽受限于采样周期。因而可通过调整各控制回路的采样周期来间接地为其分配所需的一级带宽。
假设在某一时刻有n个控制回路采用RM调度,其中第i个控制回路的综合误差为Ei,则该n个控制回路总的综合误差为。在NCSs中当采样周期增加至某个值时,系统性能虽有所下降但还是能保证系统稳定,则该上限被定义为最大允许时延(Maximum Allowable Delay Bound,MADB)[9]。由此可知,MADB即为保证系统稳定的最大采样周期值。RM调度算法的一级带宽分配原则如图3所示。URM可采用文献[10]中的方法计算得出,MADB可采用线性矩阵不等式方法求得[11]。

图3 RM调度算法的一级带宽分配
EDF调度算法的一级带宽分配方式同上。
二级带宽可以按照RM调度算法和EDF调度算法对带宽调度的可调性分析结果进行分配。二级带宽的分配是在一级带宽分配的结果之上进行的,当一级带宽发生改变时,二级带宽只需按照相应的比例改变即可。
2.3 可调度性分析
假设二维调度方法分配给RM调度算法和EDF调度算法的带宽上限分别为URM和UEDF,根据采样周期与带宽之间的关系,可得出带宽调度时所需要满足的可调度性条件。
对于RM调度算法,其可调度性条件[12]为:
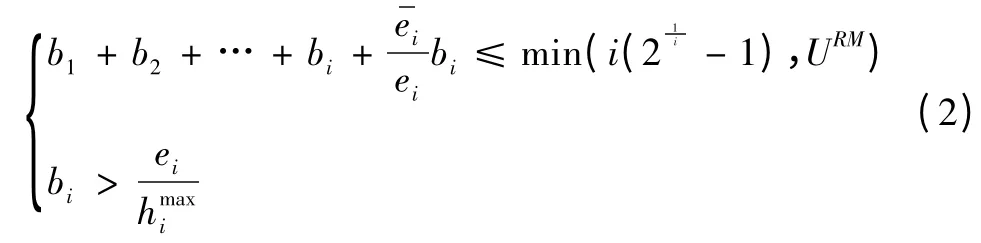
对于EDF调度算法,其可调度性条件[12]为:
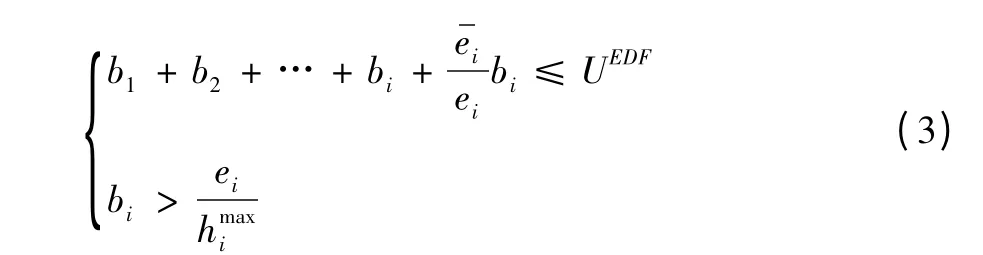
3 实验仿真与结果分析
在实验中考虑一个由4个控制回路和1个干扰节点组成的NCSs,各控制回路中被控对象的传递函数分别为:


利用TrueTime工具箱进行仿真实验。假设各控制器节点的结构相同,且控制器节点和执行器节点均采用事件驱动方式,传感器节点为时间驱动方式,输入参考信号采用阶跃信号。网络选用基于优先权的CAN网,数据传输速率为20 kbps,数据包长度设为5个字节,忽略节点的计算时间。
设含被控对象G1(s)和G2(s)的两个控制回路采用RM调度算法,含被控对象G3(s)和G4(s)的两个控制回路采用EDF调度算法。四个控制回路共用80%的系统带宽,剩余20%带宽被干扰节点占用。为简化过程,规定一级优先级分配为RM调度算法的优先级高于EDF调度算法,二级优先级由各调度算法自身的计算方法来实现;二级带宽分配为含被控对象G1(s)和G2(s)的两个控制回路共用60%,含被控对象G3(s)和G4(s)的两个控制回路共用40%。
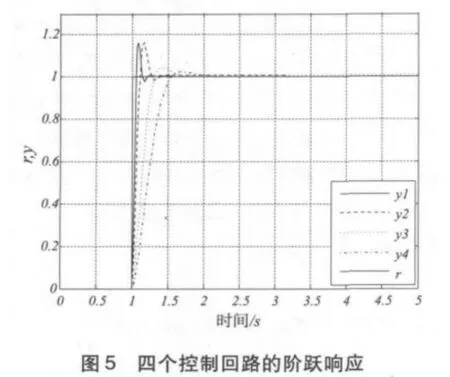
由仿真结果可知,采用本文所提出的调度策略后,各控制回路的IAEi和控制系统总的IAE值较小,系统能够正常稳定地工作,并且具备较好的控制性能。同时从图5可看出,四个控制回路都能够较好地跟踪输入信号,具备较优的响应特性。
4 结束语
本文提出的二维优先级和带宽调度机制,不仅可以进行优先级的二维调度,还可以对网络的带宽资源进行二维调度。采用这种优先级调度机制,系统中任务的执行次序由其调度策略的优先级和任务的优先级共同决定,并且采用相同调度策略的任务根据该调度算法自身规定的优先级顺序执行。在优先级调度机制中加入带宽分配,在一定程度上为其他信息流提供较高的服务质量。仿真结果表明,文中所提出的二维调度策略具有较高的带宽利用率,说明该调度机制是有效的。由于本文只考虑了理想的情况,但实际的网络控制系统是比较复杂的,难以通过计算直接得到控制性能最佳状态时的采样周期和最优带宽分配比例。因此,下一步的工作是结合实际的网络控制系统,采用智能算法来寻优。

[1]Xiong J L,James L.Stabilization of linear systems over networks with bounded packet loss[J].Automatics,2007,43(1):80-87.
[2]Gupta R A,Chow M Y.Networked Control System:overview and research trends[J].IEEE Transactions on Industrial Electronics,2010,57(7):2527-2535.
[3]芮万智,江汉红,侯重远.网络控制系统研究综述与展望[J].信息与控制,2012,41(1):83-88.
[4]褚红燕,费树岷,岳 东.基于T-S模型的非线性网络控制系统的量化保成本控制[J].控制与决策,2010,25(1):31-36.
[5]刘 念,周煦伦,沈彦德.网络控制系统集成模糊反馈调度器的设计[J].控制工程,2011,18(3):429-433.
[6]李祖欣,王万良,雷必成,等.资源约束系统的控制与调度协同优化方法[J].控制理论与应用,2009,26(1):97-102.
[7]谭朋柳,金 海,张明虎.用于开放式系统的二维优先级实时调度[J].电子学报,2006,34(10):1773-1777.
[8]Velasco M,Fuertes JM,Lin C,et al.A control approach to bandwidth management in networked control systems[C]//IEEE Industrial Electronics Society.Proceedings of the 30th IEEEAnnual Conference on Industrial Electronics Society,Barcelona,Spain,November2-6,2004:2343-2348.
[9]Branicky M S,Philips S R,Zhang W.Stability of Networked Control Systems:explicit analysis of delay[C]//AACC.Proceedings of the American Control Conference,Chicago,USA,June 28-30,2000:2352-2357.
[10]赵维佺,李 迪.CAN网络化运动控制系统的动态带宽分配算法[J].华南理工大学学报:自然科学版,2010,38(10):61-67.
[11]Kim D S,Lee Y S,Kwon W H,et al.Maximum allowable delay bound of networked control systems[J].Control Engineering Practice,2003,11(11):1301-1313.
[12]王万良,蒋一波,李祖欣,等.网络控制与调度方法及其应用[M].北京:科学出版社,2009.
