基于K-SVD字典学习的核磁共振图像重建方法

刘平，刘晓曼，朱永贵

(中国传媒大学 理学院，北京 100024)

基于K-SVD字典学习的核磁共振图像重建方法

刘平，刘晓曼，朱永贵

(中国传媒大学 理学院，北京 100024)

基于超完备字典的图像稀疏表示因其具有稀疏性、特征保持性、可分性等特点而被广泛应用于图像处理。本文利用K-SVD字典学习算法并应用于MR图像重建。将字典学习等价于一个二次规划问题，学习得到的字典能有效描述图像特征。基于学习所得的字典，获得图像的稀疏表示，并重建原始图像。实验结果表明，与Zero-filling方法相比，本文的重建结果能更好地保留图像细节信息，获得更高的SNR值。

压缩感知；核磁共振成像；重构算法；K-SVD字典学习方法

1 引言

压缩感知理论[1]是一种充分利用信号稀疏性或者可压缩性的全新信号采样理论。该理论表明，通过采集少量的信号值就可实现稀疏或可压缩信号的精确重建。该理论在信号的获取方式上突破了传统的奈奎斯特采样定理的限制，革命性地实现了对数据获取的同时进行适当的压缩，成功克服了采样数据量巨大、采样时间以及数据存储和传输等物理资源浪费严重的问题。该理论包含三个关键点：稀疏表示、观测采样和信号重建。信号重建是其中关键的一部分，它对于观测采样后信号的精确重建以及采样过程中的准确性验证均有着重要的意义。

目前压缩感知理论已广泛应用到图像处理的各个领域，其中在医学影像的核磁共振成像(MRI)取得了显著的成果。MRI(magnetic resonance imaging)的临床应用开创了影像诊断的新纪元。核磁共振成像是当今最重要的影像学手段之一，它具有组织分辨率高、可任意方向断层、空间分辨率高、对人体无放射性损害等优点。作为一种重要的临床成像方式，MRI的主要不足是它的数据采集时间较长从而导致成像速度较慢。所以此项技术需要解决的问题是：缩短采集时间[2]。通过重建算法研究降低成像所需的数据量，即在仅获得部分成像数据的情况下，通过优化重建算法仍然获得满足临床诊断质量需求的图像[3]。

我们将K-SVD字典学习算法[4]应用到重建算法中，将传统的稀疏表示方法改变为利用字典对图像进行稀疏表示，然后通过数值试验证明，在相同采样率下，本文的重建结果比Zero-filling的重建结果能更好地保留图像细节信息，获得更高的SNR值。

2 基于K-SVD字典学习的MR图像重建

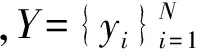
(1)

其中，T0为稀疏表示系数中非零分量的数目上限，即系数向量中的最大差异度。

从误差逼近角度看，K-SVD训练算法的目标方程还可表示为

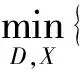
(2)

本质上，式(1)和式(2)是相同的，只是考虑问题的角度不同。论文中采用目标函数为式(1)。

式(1)求解是一个迭代过程。首先，假设字典D是固定的，用MP、OMP或BP等算法可以得到字典D上，Y的稀疏表示的系数矩阵X;然后根据稀疏矩阵X，找到更好的字典D。

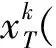
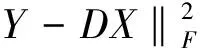
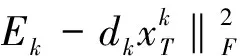
(3)

上式中，乘积DX被分解为K个秩为1的矩阵的和。按照假设其中K-1项是固定的，所剩的一个，也就是要处理的第k个。矩阵Ek代表的是去掉原子dk的成分在所有N个样本中造成的误差。

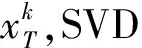
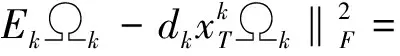
(4)

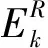
K-SVD算法非常灵活，可以和常见的稀疏分解的最优原子搜索法(如匹配追踪(MP)、正交匹配追踪(OMP)、基追踪(BP)、FOCUSS等)结合使用。本文选用的最优原子搜索算法是正交匹配追踪(OMP)算法。

基于压缩感知以及字典学习的MR图像重建需要具备两个特性：

(1)稀疏性：重建模型需要保证采样数据在字典下被稀疏表示；

(2)特征保持性：重建模型应当尽量避免伪影在重建结果中出现，例如直接对采样数据进行零填充后傅立叶逆变换所出现的现象；一般来说，伪影的出现主要是由于较低的低采样率，以及采样过程中所含带的噪声所引起的。

基于以上因素的考虑，我们给出以下重建模型：

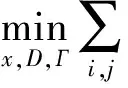
(5)

模型中的第一项是用来保证采样数据在稀疏字典D下有着最佳逼近于原始数据；模型中的第二项保证了重建数据在欠采样下的精确度。系数v的大小取决于噪声的标准差σ，即v=(λ/σ)，此处，λ是一个正常数。这使得模型对噪声有着更好的鲁棒性。这种利用先验信息来确定系数的方法已经在图像去噪中取得很好的应用[5]。本文提出的基于超完备字典学习的重建算法，将字典训练问题转化为一个带边界约束的二次规划问题，并研究适合于大规模运算的解法，使其适用于具有高维特性的图像处理问题。训练得到的字典具有非负性的特征，与采样数据相适应。实验结果表明，基于K-SVD算法训练得到的字典具有很好的去噪能力，能够更好地重建出原始MR图像的特征，重建后具有较高的峰值信噪比。

基于上述模型的MR重建算法包含两个过程：

(1)字典更新：这里，x初始假设是已知固定的，字典和采样数据的稀疏表示交互学习进行更新。

(2)重建过程：此过程中与上一步相反，字典和采样数据的稀疏表示已经得到更新结果，所以此时是已知固定的，而x就是我们要得到的重建结果。

接下来将详细描述这两个步骤。

首先是字典更新，在此步骤中，问题(5)在x固定的前提下进行求解。此时对应的子问题为：

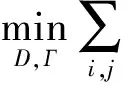
(6)

(6)中已经把稀疏表示的系数进行了误差约束，同样的方法在基于字典学习的去噪算法中也是一样的。我们用采样数据来训练字典，对应的字典中的每一列为规范化的向量。字典学习的过程应用K-SVD算法来进行学习，一旦得到新的字典，对应的稀疏表示系数αij就可确定。

接下来，在重建过程中字典和稀疏表示系数均是固定已知的，对应的重建模型(5)将变化为：

(7)

此时(7)是一个普通的最小二乘问题，接下来对其进行求解。首先对(7)一阶求导后得到的结果如下：

(8)

式中，上标H和T分别代表复数下的共轭转置以及实数下的转置运算。直接对(8)进行求解的计算量是相当大的，因为要对一个P＊P的矩阵进行求逆才可得到重建结果，而此处的P=256×256，这使得求解此问题的时间复杂度达到O(P3)。但是对问题中的各项进行仔细的分析，我们可以利用其结构的特殊性对其计算量进行简化。

接下来，可以利用傅立叶变换的性质对(8)做进一步计算量的简化。首先定义F∈CP×P为一个傅立叶变换编码矩阵，从而有FHF=βIP。将全空间的数据x的傅立叶变换Fx代入到(8)中我们可以得到：

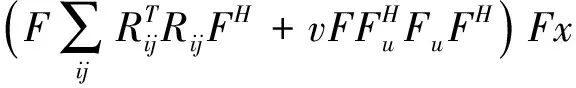
(9)

(9)中的每一小块的求解结果的傅立叶变换域的值我们可以这样来表示：

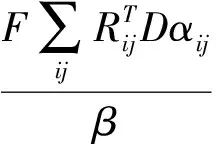
基于以上分析，可以得到(9)的求解结果如下：

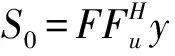
3 数值实验

为了分析本章提出算法的性能，将本章的算法和Zero-filling方法进行比较，其中Zero-filling方法采用逆傅里叶变换的思想求解MR图像重建问题。

实验用图如图1所示的三幅标准MR测试图像，采用上述算法和本文方法对三幅标准MR图像进行重建，用射线性型采样模式进行采样(图2)，采样率取35%。实验结果如下所示：

我们知道，评价图像处理效果最常用的技术指标是峰值信噪比(SNR值，式10)，峰值信噪比越大，表明重建的图像和原图像的差异越小，从而图像的重建效果就越好。针对上述三幅测试图像，对Zero-filling方法和本章方法进行比较。

(10)

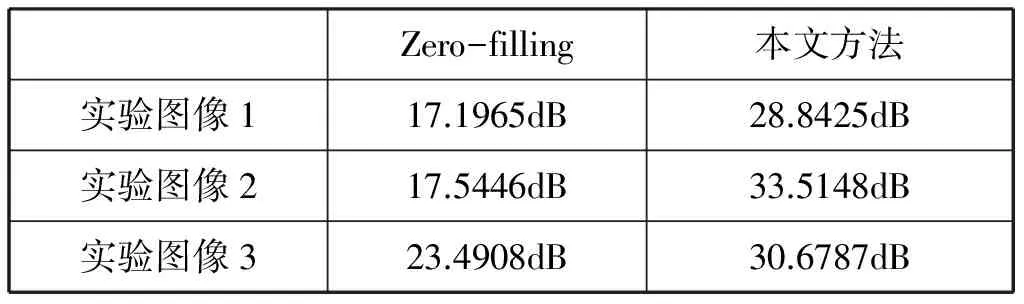
表1 未添加噪声SNR结果：

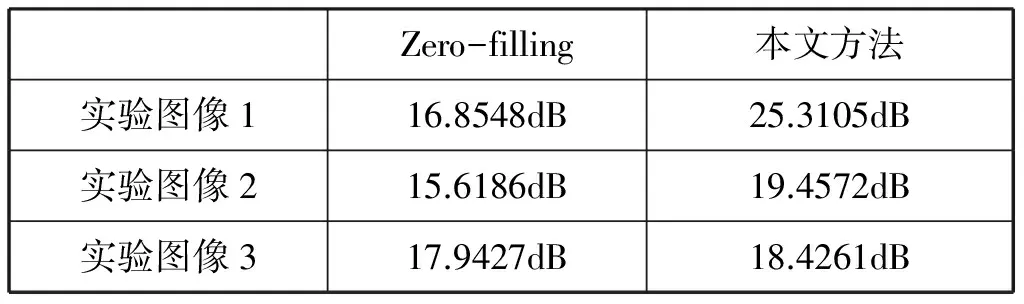
表2 添加σ=10的高斯噪声后的SNR结果

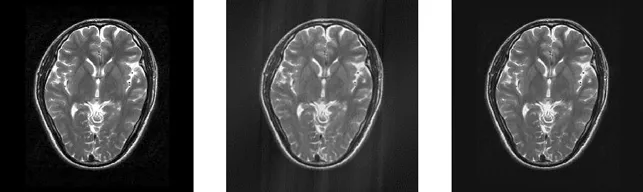
(a)原始图像 (b)Zero-filling方法 (c)本文方法

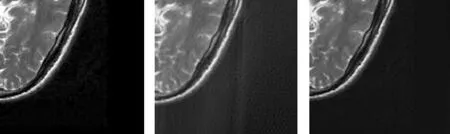
(d)原始图像细节 (e)Zero-filling重建细节 (f)本文方法重建细节

(g)训练得到的字典

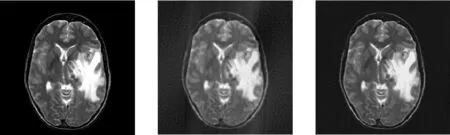
(a)原始图像 (b)Zero-filling方法 (c)本文方法

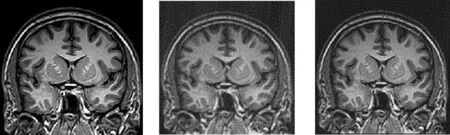
(a)原始图像 (b)Zero-filling方法 (c)本文方法

4 结论

本文基于已有的字典稀疏表示方法以及K-SVD字典学习方法，讨论了新的MR重建模型。并与Zero-filling方法进行了重建结果对比，实验结果表明：在相同采样率下，本章讨论的方法能有效地使重建出的效果好于Zero-filling方法。

[1]D Donoho.Compressed sensing[J].IEEE Trans Inf Theory，vol 52，no 4：1289-1306，Apr.2006.

[2]M Lustig，D Donoho，J Pauly.Sparse MRI：The application of compressed sensing for rapid MR imaging[J].Magn Reson Med，vol 58，no 6：1182-1195，2007.

[3]X Qu，D Guo，Z Chen，C Cai.Compressed sensing MRI based on nonsubsampled contourlet transform[J].in Proc IEEE Int Symp IT Med Edu，2008：693-696.

[4]M Aharon，M Elad，A Bruckstein.K-SVD：An algorithm for designing overcomplete dictionaries for sparse representation[J].IEEE Trans Signal Process，vol 54，no 11：4311-4322，Nov 2006.

[5]M Elad，M Aharon.Image denoising via sparse and redundant representations over learned dictionaries[J].IEEE Trans Image Process，vol 15，no 12：3736-3745，Dec 2006.

MRImageReconstructionBasedonK-SVDDictionaryLearning

LIU Ping，LIU Xiao-man，ZHU Yong-gui

(Department of Applied Mathematics，School of Sciences，Communication University of China，Beijing 100024 China)

Images’ sparse representation using over-complete dictionaries have a wide application in image processing due to the properties of sparsity，integrity and separability.This paper proposes a dictionary learning algorithm which is applied to MR image reconstruction.The dictionary learning problem can be expressed as a box-constrained quadratic problem.The learned dictionary describes the image content effectively.Based on dictionary learning，we propose a model of MR image reconstruction，and compare with the Zero-filling method.The results of numerical experiments show that，under a same sampling rate，the reconstruction by proposed method can keep better reconstructed effect and higher SNRs.

compressed sensing; Magnetic Resonance Imaging; reconstruction algorithm; K-SVD dictionary learning method

2013-06-27

刘平(1988-)，男(汉族)，陕西榆林人，中国传媒大学硕士研究生.E-mail：liupingcuc@163.com

TP391

A

1673-4793(2013)04-0034-06

(责任编辑：宋金宝)