BICM-ID系统下一种基于CE停止准则新的自适应译码算法
2013-11-03齐冀李怀军
齐冀,李怀军
(1.中国传媒大学 信息工程学院,北京 100024;2.国家计算机网络与信息安全管理中心河北分中心,河北 050000)
BICM-ID系统下一种基于CE停止准则新的自适应译码算法
齐冀1,李怀军2
(1.中国传媒大学 信息工程学院,北京 100024;2.国家计算机网络与信息安全管理中心河北分中心,河北 050000)
在BICM-ID系统中,现存的解码算法在复杂度和性能上不能得到很好的折中。Max-Log-MAP算法有较低的计算复杂度,但是在性能方面并不是很好。同时,Log-MAP算法的译码性能相比于MAX-LOG-MAP有很大的提高但是计算复杂度却大大提高。此外,Constant-Log-MAP算法在系统性能和译码复杂度上是在上述两种算法之间的。在本篇论文中,提出了一种在BICM-ID系统下,基于交叉熵(CE)停止准则的自适应译码方案,是一种能够随着信噪比(SNR)的改变采用了上述三种不同的译码算法优势的新算法。
BICM-ID;Log-MAP算法;Max-Log-MAP算法;Constant-Log-MAP算法;自适应译码算法;译码性能;计算复杂度;交叉熵(CE)停止准则
1 引言
比特交织编码调制系统(BICM)是Zehavi[1]在早期的通信系统中引入进来的。随后,为了在瑞利衰落信道下提高系统性能,BICM系统又被Caire深入研究[2]。然而,BICM系统在高斯信道下的性能并不是很理想。为了克服这一难题,提出了比特交织编码调制的迭代译码系统(BICM-ID)[3],该系统无论在瑞利衰落信道下还是高斯信道下都能取得良好的译码性能。但是由于BICM-ID系统的迭代译码次数固定使得计算复杂度比以前大大提高,交叉熵(CE)[4]停止准则的出现攻克了这一难题,该停止准则能够在合适的门限范围内减少迭代次数并能完成正确的译码输出值。
在BICM-ID系统的译码方案中,有常见的三种,分别是:Log-MAP算法、Max-Log-MAP算法和Constant-Log-MAP算法。实际上,Log-MAP算法[5]由于在对数部分保留了全部的信息,所以该算法在性能方面是最可行的。但是存在的缺点就是该算法的计算复杂度太高。随后,为了减小计算复杂度,Max-Log-MAP算法[6]被提出,这种算法相比于Log-MAP算法是将Log-MAP算法对数校正因子进行省略,从而在很大程度上降低了计算复杂度,并且这种方案在高斯信道下的性能损失基本上是可以忽略不计的。然而,当我们把Log-MAP中的对数校正因子定义为一个常数的时候,就出现了Constant-Log-MAP算法[7],该算法无论是在高斯信道还是瑞利衰落信道下,性能都接近于Log-MAP算法,并且也能够在很大程度上降低计算复杂度。
在本篇论文中,我们提出了一种结合上述三种译码算法的自适应译码算法。提出的自适应译码算法是随着信噪比(SNR)增加时,当上述三种译码算法性能相近时,我们选择复杂度相对最低的译码算法。如果在性能上有很大的差别,我们采用相对译码性能较好的译码算法。这种提出的自适应译码算法的优势在于在性能方面,它是最接近于Log-MAP译码算法的。在计算复杂度方面,相比于传统的Log-MAP算法,会有很大程度的降低。
本篇论文的结构如下:第二节,我们对BICM-ID系统的接收端进行了简单介绍,第三节对CE停止准则进行简单描述,第四节中,简单介绍三种已存在的译码算法以及详细描述提出的自适应译码算法,第五节和第六节分别给出了仿真结果和结论。
2 BICM-ID系统的接收端
BICM-ID系统的接收端如图1所示,我们假设复传输信号x经过信道的数学表达式如下:
yk=ρk·xk+nk
(1)

我们先假定搭建的系统模型接收端用卷积码编码和一般的解调方式,并且解码算法利用常规的Log-MAP算法。


(2)

图1 BICM-ID系统模型框架简图


(3)
解映射的输出值在解交织后进入软信息译码器,软信息译码器利用Log-MAP算法计算对数似然比的后验概率,软信息译码器的输出定义为:

(4)

3 交叉熵(CE)停止准则
CE停止准则始于turbo码迭代译码算法中,其停止判决原理是根据每次迭代中软输出译码器的交叉熵值来确定,其作用减少不必要的迭代次数,从而降低总译码的计算复杂度。CE停止准则是在2次软输出译码器连续迭代的对数似然比下,计算近似交叉熵的。如果交叉熵的表达式用T(i)表示,则定义为:
(5)
如果T(i)< (10-2~10-3)T(1),迭代结束。
在文献[8]中,CE停止准则被应用于BICM-ID系统,T(i)定义为:

(6)
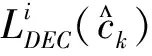
4 几种存在的译码算法和提出的自适应译码算法
4.1 Log-MAP译码算法
网格编码的MAP算法最早由Bahl,Cocke,Jelinek和Raviv[9]及 McAdam,Welch和Weber[10]提出。在文献[5]中,LOG-MAP算法分析了αk-1(s′),βk(s),和γk(s′,s)的值,计算时将对数部分进行雅各比函数变换,定义了前后向递推的数值:
(7)
(8)
在该表达式中,定义:
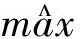
(9)
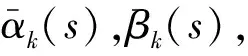
(10)

4.2 Constant-Log-MAP译码算法

=1,2and3
(11)

4.3 Max-Log-MAP译码算法
Max-Log-MAP算法是将公式(9)中的对数部分省去,在文献[6]中有详细介绍。采用该近似方法,译码性能相对于LOG-MAP算法是次优的。但是,此算法省去了对数部分,因此在计算复杂度上比LOG-MAP有很大程度的降低。
4.4 提出的自适应译码算法
本文提出的算法是结合了如上三种算法的优势,既随着信噪比增加,三种译码算法的性能非常接近时,我们采用计算复杂度相对最低的译码算法。反之,当三种译码算法在性能上有很大差别时,我们采用译码性能最好的算法,这样在总体上不仅可以保证较准确的译码性能。复杂度于传统的Log-MAP算法相比,也会有很大的降低。
简言之,该种提出的算法无论在译码性能上还是计算复杂度上都是一个很好的折中。
5 仿真结果
实验汇编语言基于matlab环境,仿真参数定义如下:采用BICM-ID系统,码率为1/2的卷积码,调制方式采用8PSK调制,SP映射,信道条件为瑞利衰落信道,帧长2048,最大迭代次数10次,采用基于交叉熵(CE)停止准则。
图2显示了上述三种译码算法的译码性能。如图3所示,提出的自适应算法的译码性能与Log-MAP算法的译码性能极为接近,并且在复杂度上相比于Log-MAP与Constant-Log-MAP算法都有很大程度的降低。仿真结果表明:当信噪比从0到3时,三种译码算法的性能相似,所以我们采用计算复杂度相对最低的Max-Log-MAP算法。然而,当信噪比区间为3到5时,我们采用Log-MAP算法,因为在性能上,相对于Max-Log-MAP算法可以获得0.6到1.1的编码增益,相对于Constant-Log-MAP算法可以获得0.1到0.3的编码增益。在信噪比区间为5到6时,Constant-Log-MAP算法与Log-MAP算法的译码性能相似,均比Max-Log-MAP算法有0.1到0.6的编码增益。最后,当信噪比为6到8时,由于三种译码性能接近,我们依然采用计算复杂度相对最低的Max-Log-MAP算法。

图2 瑞利衰落信道下三种译码算法性能比较

图3 提出的自适应译码算法性能
6 结论
在本篇论文中,我们在BICM-ID系统中,提出了一种基于CE停止准则的自适应译码算法,这种自适应的译码算法是利用不同的信道环境采用不同的译码算法。在信噪比相对较低或者相对较高时,我们采用上述三种译码算法中计算复杂度相对较低的Max-Log-MAP算法,在信噪比区间相对居中时,我们采用Constant-Log-MAP算法或Log-MAP算法来获得较为准确的译码性能。仿真结果也说明了提出了自适应算法在性能上与Log-MAP算法接近并且相比于Log-MAP算法的复杂度大大降低。
[1]Zehavi E.8-PSK trellis codes for a rayleigh channel[J]. IEEE Trans Commun,1992,40:873-883.
[2]Caire G,Taricco G,BiglieriE.Bit-interleaved coded modulation[J].IEEE Trans Inform Theory,1998,44:927-946.
[3]Li X,Chindapol A,Ritcey J A.Bit interleaved coded modulation with iterative decoding and 8-PSK signaling[J].IEEE Trans Commun,2002,50:1250-1257.
[4]Hagenauer J,Offer E,Papke L.Iterative decoding of binary block and convolutional codes[J].Information Theory,IEEE Transactions ,1996,42(2):429-445.
[5]Robertson P,Hoeher P,Villebrun E.Optimal and sub-optimal maximum a posteriori algorithm suitable for turbo decoding[J].Eur Trans Telecommun,1997,8(2):119-125.
[6]Erfanian J A,Pasupathy S,Gulak G.Reduced complexity symbol detectors with parallel structures for ISI channels[J].IEEE Trans on Communications,1994,42(234):1661-1671.
[7]Papaharalabos,Sweeney S,Evans P.Constant log-MAP decoding algorithm for duo-binary turbo codes[J].Electronics Letters,2006,42:709-710.
[8]Zhang S,J Li,Cai C.A variable iterative decoding scheme for BICM-ID based on crossentropy[C]. WCSP 2009.International Conference,Nov.2009:1-4.
[9]Bahl L R,Cocke J,Jelinek F,Raviv J.Optimal decoding of linear codes for minimizing symbol error rate[J]. IEEE Trans Inform Theory,1974,20:284-287.
[10]McAdam P L,Welch L,Weber C.M A P bit decoding of convolutional codes[C]. Znt Symp on Information Theory,1991.
AnAdaptiveDecodingAlgorithmBasedonCECriterionforBICM-ID
QI Ji1,LI Huai-jun2
(1.School of Information Engineering,Communication University of China,Beijing 100024,China;2.Hebei Branch of National Computer Network and Information Security Management Center,Hebei 050000,China)
The existing decoding schemes in BICM-ID cannot perform well both in the computational complexity and decoding performance.The Max-Log-MAP algorithm has lower computational complexity with worse decoding performance.Meanwhile,the decoding effect of Log-MAP algorithm is greatly improved but it has much computational complexity.Besides,the Constant-Log-MAP algorithm is between the two algorithms mentioned above which can make a balance in the system’s computational complexity and decoding performance.In this paper,we propose an adaptive decoding algorithm based on cross-entropy (CE) stopping criterion for BIDM-ID system.The proposed algorithm employ different decoding algorithm as SNR changes to take advantage of the three algorithms above.
BICM-ID;log-map algorithm;max-log-map algorithm;constant-log-map algorithm;adaptive decoding algorithm;decoding performance;computational complexity;ce stopping criterion;
2013-01-23
齐冀(1989-),男(汉族),辽宁沈阳人,中国传媒大学硕士研究生.Email:qiji_cuc@126.com
TN921
A
1673-4793(2013)02-0024-05
(责任编辑:王 谦)
