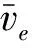无源媒质中电磁波的异常传播
2013-11-03黄志洵
黄志洵
(中国传媒大学 信息工程学院,北京100024)
无源媒质中电磁波的异常传播
黄志洵
(中国传媒大学 信息工程学院,北京100024)
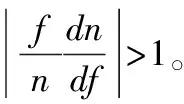

Brillouin的信号速度定义存在问题,数学意义超越物理意义。我们的反驳是,最重要之点在于传播中不失真的波群(波包)。由此出发的理论分析证明,众多NGV研究者已观察到的超光速传播其实就是实现了超光速通信。……超光速群速传播和负群速波传播,这两者各有其用途。科学家们把这与多个领域(如光通信、光场压缩态、量子纠缠)相联系,并得出结论说,高效、低耗的快光的潜在应用是广阔的。
负群时延;负群速;无源媒质;快光
1 引言
如所周知,电磁波的相速指等相位面的传播速度,用vp表示。单色光的情况单纯,整个光波以同一速度传播,即vp=ω/k(k为波矢的大小),通常也写作vp=ω/β(β为相位常数)。但是一个时间上从(-∞)延伸到(+∞)的理想单色波决无实现的可能,实际的波都是已调波,即一个较低频率(Ω=2πF)对较高频率(ω=2πf)的载波进行调制。Fourier分析表明可以把电磁脉冲(f从短波到光频)展开为诸多不同频率的单色波的叠加。在k(或β)与f有关的色散媒质中,各单色波有各不相同的相速,即vp(ω);而整个已调波(电磁脉冲)的速度只能用群速(vg=dω/dk或dω/dβ)来表示。群速定义要求波群中的单色波处于一个窄频带中,亦即当一组ω、β相近的波运动时呈现出仿佛共同的速度,即群速。因此相速的意义非常有限,群速是研究工作中的必要工具和手段。已调波包络也称波包(wavepacket),其传播状况由媒质的色散关系决定。
在20世纪末到21世纪初的期间,人类对光的认识水平和操控能力得到提高和加强。1999年《Nature》发表了在超冷原子气体中把光速减慢到17m/s的研究成果,2001年《Phys.Rev.Lett.》刊发了光速为零(使光停下并储存起来)的文章。与此同时,关于快光(fast light,超光速的光)的文章大量涌现,主要包括两个方面:①对群速超光速(vg>c)的研究和实验;②对真空中光速c本身的探讨。此外有一个重要的动向,即通过实验在各种不同条件下得到了负群速(negative group velocity,NGV)和负群时延(negative group delay,NGD)。我们知道,1914年诞生的Sommerfeld-Brillouin经典波速理论,最先指出当vg比无限大还大时,就进入负群速区域;但在当时提不出相关的实验来说明。现在情况不同了,例如最近几年就出现了以下工作:2006年G.M.Gehring等[1]用掺铒光纤放大器技术在增益系统条件下用反常色散获得vg=-c/4000;2007年Y.Xiang等[2]针对metamaterial的隧穿由计算得到负GHS和负隧穿时间;2009年G.Monti等[3]在微波用环腔耦合微带线分析和实验,得到负群速及负群时延;2010年H.Choi等[4]用负群时延改进电路总体性能;2011年张亮等[5]用10m长单模光纤做实验得到vg=-0.151c;2012年H.Y.Yao等[6]在微波用3段矩形波导级联得到vg=5.29c;2012年A.Carot等[7]在微波用矩形波导、圆波导级联结构在实验中获得负群时延,τg=-2.2μs,负群速vg=-0.03c;2012年R.T.Glasser等[8]在光频实验,采用4波混频技术获得vg=-c/880;……以上搜集的情况肯定是不完全的,却是较重要的进展。
所谓无源媒质(passive media)是相对于增益媒质(gain media)而言的,后者的典型例子是WKD实验[9]中所用的方法——采用一个玻璃小室充入铯气,由外加磁场和2个激光束使铯气成为原子气体、在2个增益线之间创造一个反常色散区。具体讲,这两个pump光束使原子气体处于粒子数反转状态,当探测光束(第3个激光束)通过小室时,铯原子会从pump光束中吸收光子而激发,随后又放出光子。这就使探测光束得到增强,就产生了增益效应(effect of gain);WKD实验也就成了创立增益媒质的实验技术的典型事例。至于近年来采用光纤的NGV实验,如使用了放大器也是增益媒质,否则仍是无源媒质。实际上与增益系统相比,无源、无增益系统较易实现,波形失真也可尽量减小,故越来越多被采用;具体形式如:同轴线、微带线、波导、光纤、双棱镜、玻璃平板、光子晶体、等离子体等都可用。
笔者不久前曾发表论文“负波速研究进展”[10],本文是该文的姊妹篇,进一步从理论和实验方面讨论了相关的发展和发现。两文的内容稍有重复,但主要部分完全不同。
2 波传播中负群时延的电路模拟
设有一理想的恒流源加到并联谐振回路(电阻R0、电感L、电容C并联)两端,is瞬时值为
is=Iscosωt
则电回路电压为
u=Ucos(ωt+Ф)
式中


(1)

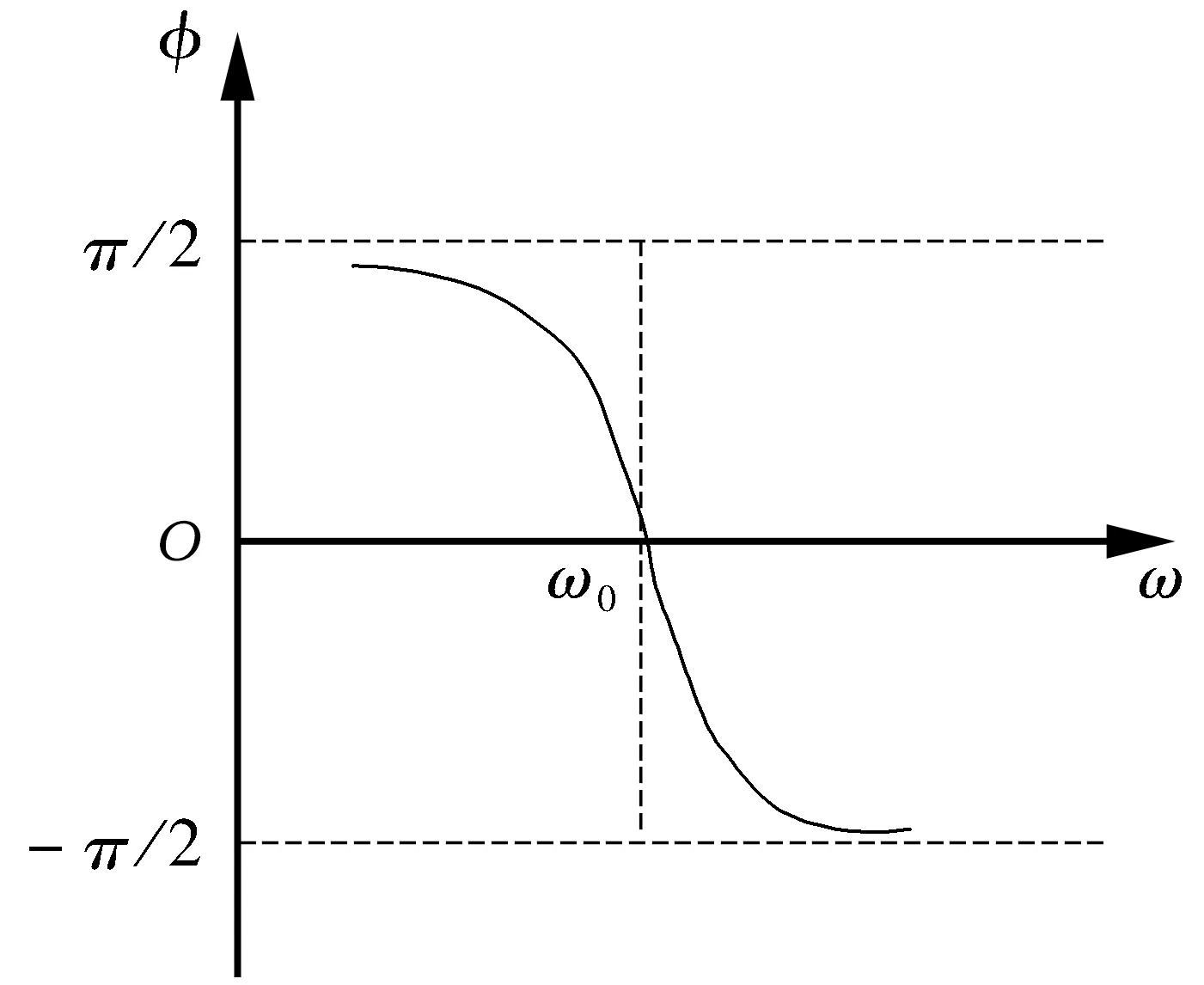
图1 并联谐振回路的相角曲线
(2)
根据谐振回路的相频特性可讨论群时延,此时信号源可假定为调幅波:
is=Is(1+mcos Ωt)cosω0t
而谐振回路仍只对ω0谐振;可以证明,输入信号经过回路的作用,输出波形、谐振频率ω0、调制频率Ω均不变,但包络cos Ωt的相位发生了滞后;表现在u~t波形图上,对应的波峰右移时间间隔τ。采用群时延定义
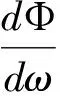
(3)
根据Ф~ω公式,可得
(4)
由此知τ(ω0)=-2Q/ω0,它是相频特性曲线在ω0点的斜率。进一步可证,调幅波通过谐振回路引起的包络延迟时间近似等于谐振回路在ω0的群时延(τ)。另外,在实际工作中希望相频特性是常数,即在一个窄频带内群时延为常数(τ=const.),则不产生相位失真。
以上讨论得出的τ为负值,这是由定义造成的,符合图1中Ф~ω曲线的规律。但在实际上也可这样定义群时延:
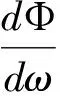
(5)
则不会产生概念上的矛盾——如果我们认定相移造成的时间滞后是正时延,在特殊情况下产生的时间超前为负时延,则如何定义τ(ω)将不成为问题。另外,在英文中,与group delay(群延迟)对应的词是group advance(群超前),后者正是对上述特殊情况的确切表达,并成为世纪之交时科学家们争相研究的课题。
必须指出,虽然基本概念的讨论是在简谐信号(单色波ejωt或e-jωt)条件下进行的,其结果也适用于脉冲信号(它本为多个简谐信号的Fourier合成)。在频域的讨论中,取输入、输出电压为

频域的网络(无源电路或有源放大器)传递函数(transfer function)取为T(ω)时,就有以下线性方程成立。
U0(ω)=T(ω)Ui(ω)=A(ω)ejφ(ω)Ui(ω)
(6)
振幅A(ω)、相移φ(ω)均为实函数。例如,设计一个带反馈回路的带通放大器电路[11](bandpass amplifier with feedback loop),如图2;这个电路的功能转为带阻滤波(band stop filter),并使图1形状的相移频率曲线改变,成为图3中的实线(图中的虚线代表开环增益系数,即A)。由于曲线有极大点(a)和极小点(b),显然存在两个零时延(τg=0,下标g代表group频率,即ω1、ω2);当ω=ω1~ω2,ω增大时Ф增加,dФ/dω>0,这时得到正群时延,是人们习惯的group delay;但当ω<ω1及ω>ω2,dФ/dω<0,得到负群时延,是group advance。因此只用一套简单便宜的运算放大器(带谐振回路及反馈),就可模拟波传播中的负群时延状况。图4是与图3对应的τg~ω曲线形状,横坐标与图3的横坐标是完全对应的。在图4中清楚地显示,τg<0的频域为(0~ω1)及(ω2~∞)。现在可写出反映网络的传输特性的方程:
u0(t)=A(ω0)ejφ(ω0)ui[t-τg(ω0)]
(7)

图2 一种有源带阻滤波电路

图3 图2电路的Ф~ω曲线
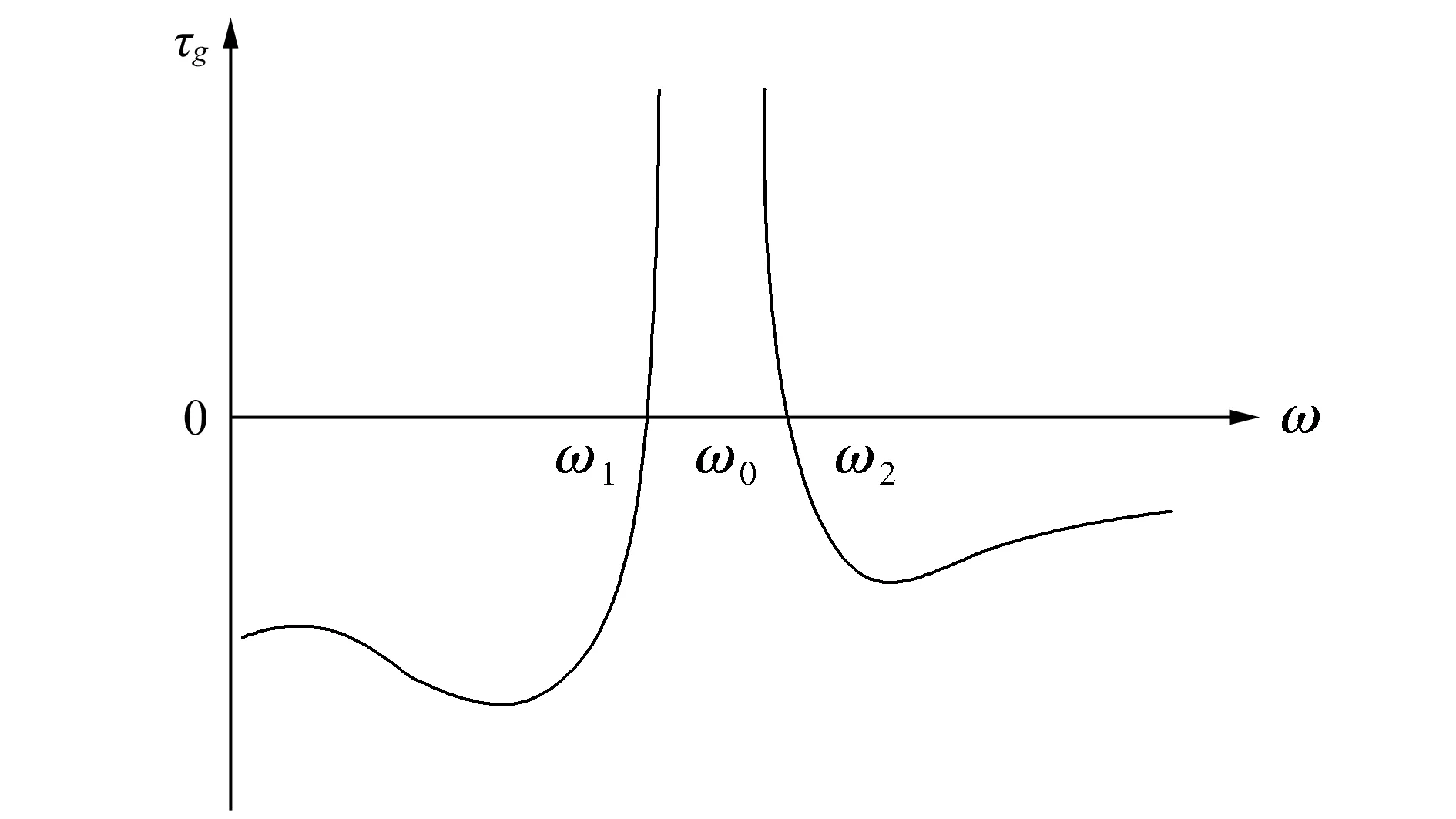
图4 与图3对应的τg~ω曲线
从以上讨论可得到某些规律性的认识;首先,负群时延(为方便起见简称为群超前)是发生在不具有放大作用的阻带(stop band)。其次,输出波形显露在输入波形之前(the origin of output waveform before the input)。图5是波形示例,虚线显示输出波形超前于输入波形——这正是负时延、负群速的特征,亦即group advance的特征。也就是说,所设计的电路可使波形超前,从而在峰值和其他特性到达输入端之前就出现在输出端(amplifier can advance a waveform so that the peak and other features appear at the output before the corresponding features arrive at the input);这是令人惊奇的现象。

图5 图2电路造成的输出波形超前
3 用同轴线级联电路模拟光子晶体
在固体物理学研究中人们常把电子和光子这两种本质上很不相同的粒子作比较,发现它们之间有许多相似的行为。自由电子的波函数是平面波,自由光子的波函数也是平面波(E分量和H分量)。晶体中的电子和晶体中的光子,波函数都是Bloch波。由于人们希望能像控制电子那样制光子,产生了光子晶体(photonic crystal,PC)的想法,在1987年提出了最初的设计。实际上,描写光子在周期性介质结构中运动的方程(Maxwell波方程)与描写电子在周期性势场结构中运动的方程(Schrödinger方程,SE)非常相似,因而在固体物理中适用的求解SE的方法都可用于PC的计算中。简单说,PC是电介质材料周期性排列形成的人工结构,由于周期性,将产生光子能带和光子带隙(band gap)。理论和实验都证明了光子禁带(stop band)的存在,其中没有电磁波传播;这就影响了光与物质相互作用的方式。
然而后来出现了用电路结构以模拟PC的考虑,该结构必须有周期性,其结果是创造出通带(pass band)和阻带(stop band)。特别是,这种结构能提供“反常色散媒质”的特性。2002年,A.Hachè等[12]正是用他称为coaxial photinic crystal(CPC)的结构,实现了较长距离上的群速超光速传播。CPC被认为是光学PC的宏观模型,它是一种有诱惑力的替代品,这是因为它的宏观尺寸和附加的灵活性:电场的相位和幅度可以任意在整个系统的外部或是内部进行测量。尽管是一维的而且没有偏振效应,但是其特性还是可以用Maxwell方程组来进行描述,而一些线性和非线性指标也与曾经有过相关报道的光学光子晶体有相似之处。同轴光子晶体最为显著的一个特性就是其禁带区向低频方向的扩展。在光学光子晶体中,禁带是由于折射率的突变而带来的反射造成的;而在同轴线里,则是由于阻抗的不匹配造成的。当信号到达不同介质的分界处时,就会有一个相移和部分反射,二者的计算由以下两个公式得到:

(8)
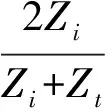
(9)
式中Zi、Zt分别为入射阻抗和传输阻抗。故媒质中阻抗的周期性变化就会对某一波长的信号产生作用。由此而产生的结果是,随着频率的变化通过晶体的相位累计也随之快速地变化。这一点在禁带附近尤其显著,反常色散和超光速都会在这个区域产生。
实验中所用的同轴晶体由几单元组成,每单元都有两个部分:特性阻抗为50Ω的RG58/U电缆和特性阻抗为75Ω的RG59/U电缆。每一部分都有相同的相速0.66c和长度5m。由于不匹配的缘故,在每个接头处都有20%的损耗,将12个这样的单元串接起来共120m。传输的频谱,在9MHz和11MHz之间有一道很深的禁带,在这里传输系数模|T|很小。使用等效折射率(effective index of refraction)概念,其实部为

(10)
式中L为PC的总长度,φ为总相移,并有

(11)
式中m=0,1……,由边界条件决定。
现在,传输系数|T|、折射率n(即nr)、群速vg都是可计算的参量,它们与频率的关系见图6;小圆点线是|T|,f=(9~11)MHz是禁带,|T|很小。用滤波器技术的语言,这是一种带阻滤波器。长虚线是n,显示出只在阻带中才有反常色散特性。实线是vg/c,显示出只在阻带中才有群速超光速特性。
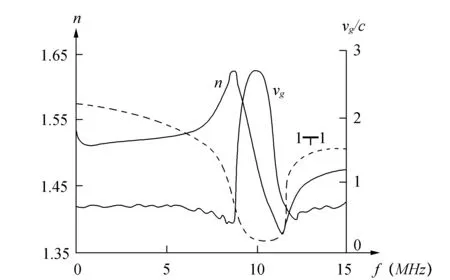
图6 Hachè电路的特性
通过测量脉冲信号在同轴晶体中的传输时间就可以确定传播速度。同一个可编程信号发生器发出Gauss脉冲包络的正弦载波。载频在5~15MHz范围内变化,脉冲宽度为6~2μs,并调节带宽在0.15~0.45MHz保证在一个包络中有30个载波。实验结果与理论计算相符合,在禁带外vg
美国《Appl.Phys.Lett.》杂志在2002年1月发表Hachè文章后,9月又发表J.N.Munday等[13]文章,再次报道相关实验。后者首先指出,不仅增益系统有负群速(NGV)现象,在无源系统中也有。过去的M.W.Mitchell[11]的工作,称为“带阻滤波器的禁带”(forbiden region of a bandstop filter),已由实验清楚地呈现出负群时延。Munday实验采用两种同轴电缆:RG58(50Ω,0.66c)和RG62(93Ω,0.85c),使阻抗失配提高、群时延加大;电缆切割长度分别为6.19m和7.97m,以获得所需周期性。这样,CPC总长L=119.5m。测vg的电路较简单,见图7;SG1产生频率较低的正弦信号(f=110kHz),作为调幅(AM)包络;SG2产生频率稍高(5~15MHz) 的已调信号,实际是AM波(调幅度100%)。两路信号加到双踪数字示波器上,其中一路加有CPC,信号通过是隧穿过程。这个实验以获得NGV为目标,比Hachè实验进了一步。观察到的现象是:脉冲峰通过CPC在时间上提前。

图7 Munday的实验电路
Munday实验中的禁带约为(6.5~9.5MHz),而在禁带边缘处的群速变化是生动有趣的——当f=6.3MHz(尚未进入禁带),vg=0.77c;当f=6.5MHz(已进入禁带),vg=4c;当f=6.8MHz(完全进入禁带),vg=-1.2c。最后一种情况,隧穿脉冲(输出脉冲)比输入脉冲早到0.32±0.02μs(peak of tunneled pulse arrived 0.32±0.02μs prior to the peak of input pulse entering CPC)。显然,在禁带中央n~f曲线斜率最大将使负群速的出现更具有可能性。
我们已在其他文章中给出实现群速超光速和负群速的条件[14],它们可概括为以下两个公式;为使vg>c,要求

(12)
而为使vg<0,要求dn/df<-n/f,亦即要求
(13)
对比以上两式,显然后者要求更高,即|dn/df|应更大些。后一条件表示,为获得NGV要求
(13a)
按照以上原则可以计算Hachè实验的情况,因为其论文给出了n~f曲线的数据。首先算出反常色散区|dn/df|=8.5×10-8Hz-1,而|1-n|/f=5×10-8Hz-1,满足vg>c的条件,故实现了群速超光速。但是
因此不可能有vg<0的结果。Munday实验则不同,其n~f曲线虽未给出,可以判断它更陡峭,达到了要求。
回过头来看2000年的WKD实验[9],反常色散区的折射率变化为1.8×10-6,而频率变化为1.9 MHz,故|dn/df|=9.5×10-13Hz-1;这个值很小,但f很大(光频),故式(13a)可满足;故他们在实验中得到负群速,vg=-c/310。具体计算如下:取λ=852nm=8.52×10-7m,算出f≅3.5×1014Hz,故有

这与WKD论文一致。另外,现在有

充分满足实现vg<0的条件;至于如此“充分”的原因,是由于增益系统的作用。
现介绍中国传媒大学在2003年进行的实验及其结果[15]。阻抗分别为50Ω(RG-58A/U)和75Ω(RG-59B/U)的同轴电缆相互串联组成混合电缆,由于二者的阻抗不匹配从而形成反常色散区。测量经过混合电缆的已调信号与未经混合电缆的基带信号之间的时间差,在已知两路信号所经过的路程长度的其中未经混合电缆的基带信号在传输电缆中传播速度的情况下,由公式计算出电信号在混合电缆中的传播速度。采用图7,取l1=l1a+l1b(l1a=4m,l1b=75m),令
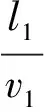
(14)
由此可得所要求的信号在混合电缆中的速度:

(14a)
如l1、l2已知,测出△t即可得v1;用数字式双踪示波器(HP54180A)可以实现测量△t。以上各式下标1表示经过混合电缆的已调信号所经过的路程长度和速度;下标2表示未经混合电缆的基带信号所经过的路程长度和速度,其中v2=0.66c。
实验步骤:①将混合电缆通过转换头接好(共15段,75m),调节信号发生器1(HFG813),使其发生频率为200kHz基带信号用以调制载波,调节信号发生器2(HFG813),使其所发出的载波在6 MHz~13MHz之间变化。②测量固有时间差:按照图7所示连线,将信号发生器1所产生的基带信号分为两路,一路直接进入示波器的一个输入端。另一路接入信号发生器2,用以对载波进行调制;将信号发生器2产生的调制后的信号直接接入示波器的另一个输入端(不经过混合电缆)。在示波器上同时观察两路信号的波形,读出二者的时间差。这个时间差并不是我们所要求的,它的产生有两方面原因:首先是由于两路信号所经过的路程不同,两次基带信号调制载波时也会产生一个触发时延,所以我们称之为固有时间差△t1,为0.1515μs;③重新连接,将信号发生器2产生的已调波通过混合电缆后再接入示波器,这时观察两路信号的时间差△t2,将此时间差与步骤②中所得时间差相减,即可得到公式中所需的时间差△t(△t=△t2-△t1);④调节信号发生器2,在6MHz~13MHz范围内,每200kHz取一个采样点,分别在示波器上测得不同频率点(阻带内和阻带外)上基带信号与载波信号之间的时间差,将结果代入公式(14a),从而得到所对应的频率点的电波在混合电缆中的传播速度;⑤记录数据,再由matlab仿真处理这些数据点,绘制数据曲线。
实验前先按传输线理论作仿真计算。设n段传输线级联,对应电压un、电压in,则连续性边界条件导致有以下两方程成立:
ane-jknz+bnejknz=an+1e-jkn+1z+bn+1ejkn+1z
(15)
-bn+1ejkn+1z)
(16)
式中z为传输方向,an、bn为入射波、反射波振幅,k为波数,Z为特性阻抗。由此编程计算,可求出传输系数T、反射系数ρ、折射率n(nr)乃至群速vg与频率的关系。取Z1=50Ω,Z2=75Ω,n=12;算出的n(虚线)和vg/c(实线)见图8。实验结果是阻带内v1=(1.5-2.4)c,是群速超光速。关于负群速,有一次观察到波包比参考波形超前(调制波落在载波后头);但不很肯定。
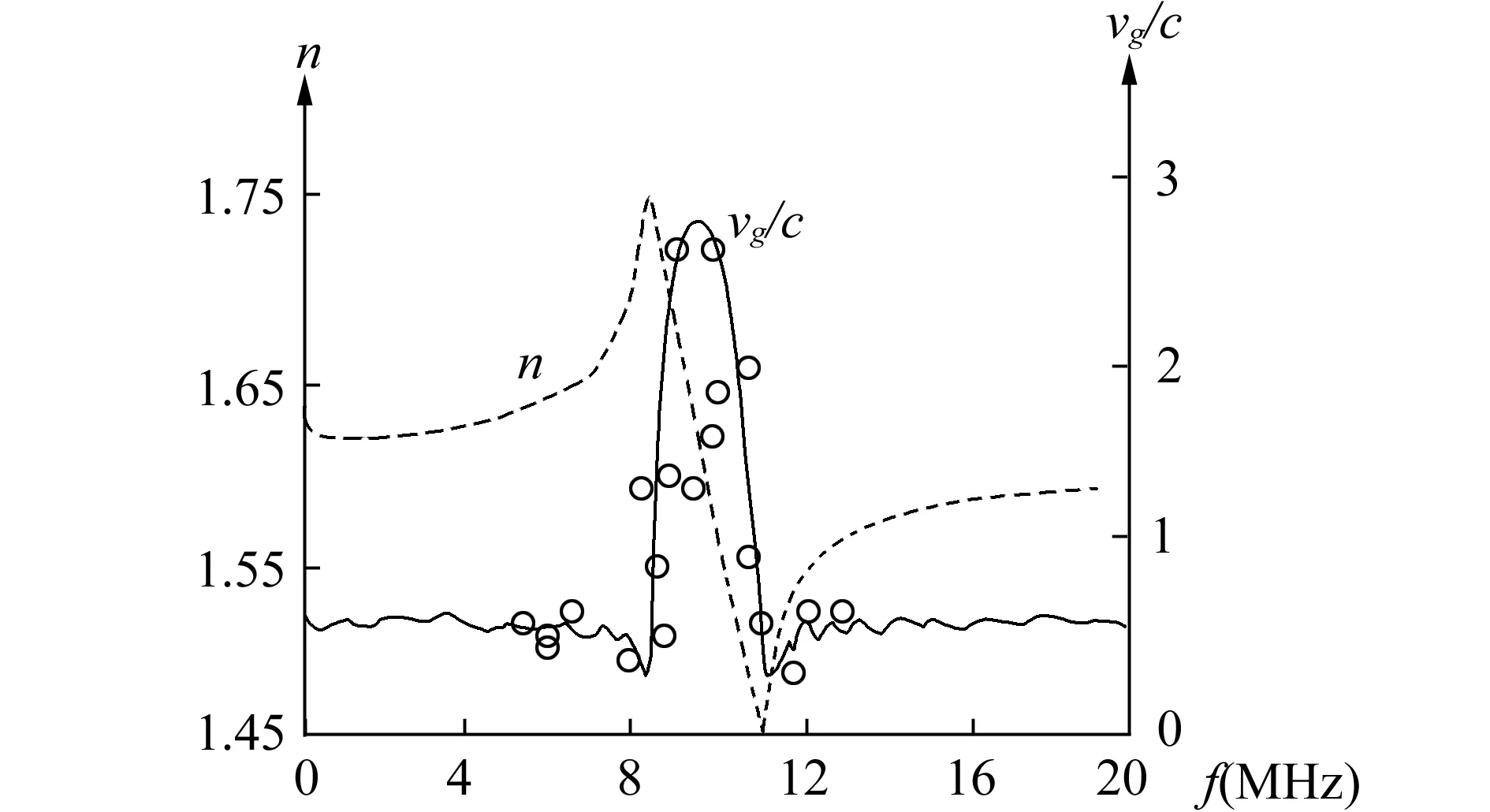
图8 中国传媒大学研究组的计算和实验情况
众所周知光子晶体(PC)是一种周期性结构。现在使用多段(每段长数米)的不同阻抗的同轴线互相级联(cascade),也形成一种周期结构。连接处的不连续性交替、重复出现,对波的传输幅度和相位产生重大影响,这时同轴线内已不是纯粹的TEM波了。反常色散曲线(n~f曲线)的陡峭程度与阻抗比值、短截电缆长度、截段的数目都有关系,改变这些因素可以提高曲线的陡峭度。从Munday实验和我们实验的情况看,同轴光子晶体(CPC)是可以获得负群速(NGV)的方法之一。
现在我们再作核算;中国传媒大学研究组的2003年研究,dn/df≅-1.45×10-7Hz-1;如取n=1.6,f=9.5×106Hz,则有
故不会有vg<0的结果。为了使这个比值大于1,要求|dn/df|>1.68×10-7Hz-1,这比上述值只大14%,应当可以做到。
图9给出数字示波器显示的传输波形:图9(b)、图9(c)是阻带内的波形,与超光速群速相对应;图9(a)、图9(d)是阻带外的波形,与亚光速群速相对应。


图9 实验中的波形观测
2009年周渭等[16]报道了用相同技术做CPC实验的结果,不仅获得了超光速群速而且获得了负群速。两种电缆仍为50Ω和75Ω各一,负群速的获得是靠增加线长。该文与Munday一样,没有电脑软件的仿真计算,而是在实验中测试了6种总长(55.8m,80.6m,105.4m,130.2m,155m,179.8m)的情况,在最后的总长为179.8m时出现了时间差为负的一个点,为(-1.45c)。表1给出4个研究组(分属加拿大、美国、中国)的实验研究情况。

表1 用级联同轴线模拟光子晶体的实验
4 用波导级联结构获得超光速群速及负群时延[6,7,17]
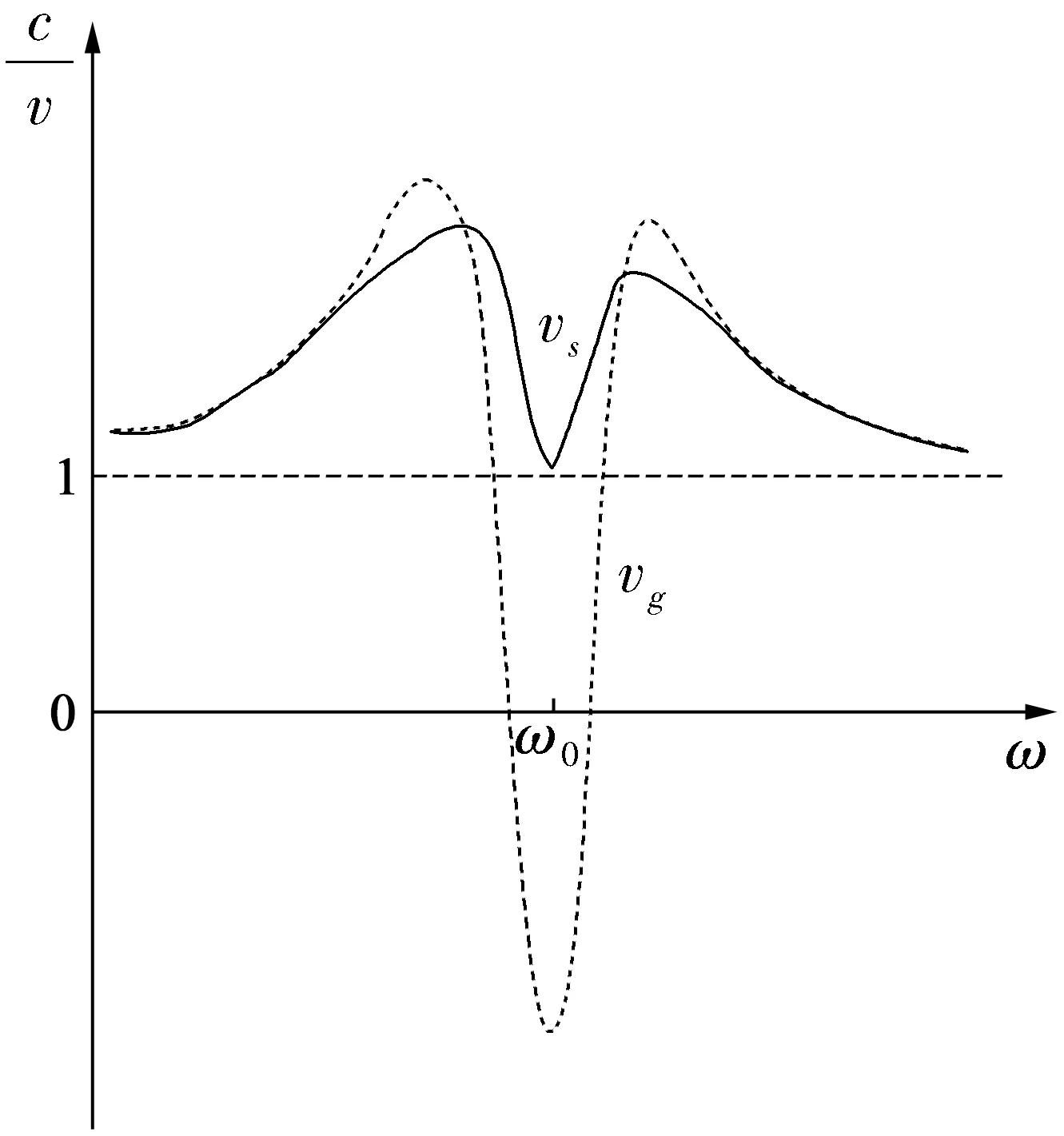
由于有可以用到微波的同轴线,而波导(waveguides)是天然地用于微波的传输线,从表面上看,二者相似。实际上它们很不相同;同轴线中是一种承载TEM波的无色散传输,场解满足Laplace方程,对应标量Helmholtz方程中本征值为零(h=0)的情况,属于非本征值问题。波导则代表一种有截止特性的波动过程,是强色散性的器件(媒质),场解不满足Laplace方程,对应h≠0的情况,是本征值问题。在技术实践中,一根波导可以是多模波导,也可以是单模波导;亦即选择波导尺寸可以使之仅传输一个模式。例如对矩形波导而言,则传输主模TE10的条件是:宽边尺寸a满足λ/2 1985年黄志洵[17]的论文“波导截止现象的量子类比”,比欧美科学家早几年提出了“用量子隧道效应观察和研究波导”,并建立了量子隧穿的等效电路(等效网络)模型。这体现了以Maxwell经典波电磁波方程与描写量子波动的Schrödinger波方程的相似性,消失态(evanescent state)既出现在金属壁波导(当f 图10 三段矩形波导互相级联 2012年出现的两篇论文([6]和[7])引人注目地提出了在微波用波导进行实验的新方法,基本上不是利用消失模。是否可纳入反常色散的框架内而理解?现在还不好说。先看Yao和Chang[6]的工作,所设计的结构是3段矩形波导互相级联,如图10;波导Ⅰ、Ⅲ是相同的WR282波导,宽度a=72.14mm,高度b=34.04mm;据此我们查阅手册,知其主模TE10的工作频率范围f=2.6~3.95GHz,截止频率fc=2.078GHz。波导Ⅱ的型号不变,宽度不变,故fc和原来一样,但高度(人为地)减为3mm,是很薄的结构。作者说,几何结构的改变在边界上引发了模式效应(model effect),即部分的基本工作模式(TE10)需转换为波导的高阶模(TEmn与TMmn),以共同满足结构变化后的金属边界条件。此模式转换过程会导致所操作的TE10波的反射率增加,进而使整个系统形成类1维开口谐振腔(Fabry-Perot open cavity),而电磁波在这个谐振腔中多次反射与互相破坏性干涉过程即被认为是造成群速超光速(实验测得vg=5.29c)的基本原因。图11是实验系统的示意图。 图11 Yao和Chang的实验系统 2012年10月下旬,笔者用电子邮件与H.Y.Yao(姚欣佑)讨论;首先表示我们对其论文很感兴趣,认为工作出色;但提出几个问题:①实验结果可否按反常色散解释?如果可以,为何论文未提及该效应?②三段矩形波导如直接相连,会出现两个小窗口,这就难于进行实验,令人费解;③波导Ⅱ高度只有3mm,波导Ⅰ、Ⅲ高度却有34mm,二者为何如此悬殊?……对此,Yao回答说:“我们的实验没有在波导中填入吸收或增益性物质,故未按反常色散解释超光速现象;如用反常色散解释,可以把两口边界上几何不连续性造成的多次反射等效为电磁波包在一填充材料的波导内传播,并依色散关系而模拟,找出等效折射率nr,它是频率的函数,物理上包含了原来的模式转换及多次反射效应。由于发生超光速现象时,通常透射信号小而反射强,故等效材料会有由于高反射损耗导致的强吸收”。此外,Yao介绍了实验中采取的技术措施。……对此,笔者提出:“我们仍然认为你们的实验可以用反常色散解释。理由是,三段波导阻抗不同,这种失配和相位上的变化,可能造成等效折射率n随频率f增大而下降。现在需要的是理论分析和电脑计算,建议你们试试。另外,你们为什么不进一步努力,争取用此结构测出负群速?当然,这要程度更大的反常色散”。对此,Yao回答说:“用这种等效原理算出的折射率与系统长度有关,这会降低等效折射率的普遍性和实用价值;不管怎样我们会作计算。另外,我们也做负群速研究,预计在某些特殊几何结构的波导中应能观测到该现象,现正在设计实验”。 图12 圆波导的Ф~ω曲线 2012年的A.Carot 等[7]的论文,题为“Negative group velocity and spin-flip in microwave adaptors”;adaptor一词译为“适配器”不妥,在微波技术中有常见的波导—同轴转换器就是adaptor,故译为“转换器”或“转接器”就可以了。因此Carot论文题目的中文应为“微波转换器中的负群速与自旋反转”,从内容可知在这里adaptor有两种:矩形波导/圆波导转换器,圆波导/矩形波导转换器;两种波导均为fc=6.5GHz,而adaptor的工作频段为8.2—12.4 GHz。文章的摘要说,具有两个微波波导adaptor的类Fabry-Perot干涉仪作为反射器造成了一种无源介电媒质,由于极化位移产生了负群时延。通过其中一个adaptor,极化矢量的旋转应变耦合出极大的负群速。在三段级联波导中,Ⅰ、Ⅲ是矩形波导(TE10模),Ⅱ是圆波导(TE11模,L=20m)。文章叙述了螺旋极化的变化,以及由两个不同的圆波导模产生了负群速。……图12是A.Carot等[7]给出的曲线,虚线是常规圆波导(vg=0.68c)的Ф~f变化规律,实线是采取措施以后获得的Ф~f变化规律,相应的圆波导长20m,相当于667个波长。在图中,反映负群时延和负群速的过程发生在f=9.884 GHz附近。图13(a)显示以48kHz信号调制(调幅)微波9.893GHz时的时间延迟,虚线是在20m长波导输入端测得的波形,实线是产生τg≅-2μs(相当于vg/c=-0.03)的快波波形。可以看出负群速的特征——快波最大值在进入波导之前就离开了它(the maxima of fast wave leaves the 20m waveguide before it has entered it)!应指出,这是在无源媒质(passive medium)中实现的。图13(b)显示当一个脉冲信号通过时输出波形(实线)与输入波形(虚线)的比较,用意也是观察负群时延情况及波形失真的大小。 图13 Carot实验获得的时间超前 现在给出波导级联结构造成负群时延的初步理论分析。在图10的Ⅰ、Ⅱ相联端面,传输系数、反射系数、相角为Ti、ρi、Фi,在Ⅱ、Ⅲ相联端面则为T0、ρ0、Ф0;考虑不连续性时,电磁脉冲入射后必然是有部分能量通过、部分能量被反射,故Ⅰ的波函数可写作 ψI=Ei(ejβz+ρe-jβz) (17) 上述写法忽略了波导损耗;而在Ⅲ处仅有传输的(透射的)分量: ψIII=TEiejβz (18) 式中T=|T|ejφt;而反射系数ρ=|ρ|ejφ;并且在无耗条件下有 |T|2+|ρ|2=1 (19) 而双口网络在波传输中发生的总相移(total phase)可写作: φ=βL+φt (20) 由此造成的群时延为 (3a) 这与前面的论述,即公式(3),概念上是一致的。H.G.Winful[20]曾给出以下结果: (21) 式中W=We+Wm是总的对时间平均的能量(We为电能,Wm为磁能);而Pin是对时间平均的入射功率,且Pin∝ε0|Ei|2。总之,τg称为传输群时延(transmission group delay),以便与反射群时延(reflection group delay)相区别;后者的定义为 (22) 2012年,H.Y.Yao和T.H.Chang[6]导出如下公式: (23) 式中φr0表示是Ⅱ的输出端的φr;上式被A.Carot等[7]所引用,并指出当以下不等式成立: (24) 则群时延为负;这只是理论上证明了这种可能性,具体的技术实现尚属困难之事。 Carot等力图以量子理论为基础进行思考,他们回顾了1936年R.A.Beth的工作(Phys.Rev.,50,115,1936),实验为光子角动量即自旋的定量提供了证据;而光子自旋与光子电场的螺旋极化有关,这关系被用来反转在圆极化光束中所有光子的自旋经过2ћ(从-ћ到+ћ)。采用的结构是两个adaptor被圆波导(起FP干涉仪作用)分开;但负群时延现象仅在下述条件下发生:两个转换器的极化互不平行,角度0<α<π时可观测到NGV;圆波导可在0~π/2角度上旋转(实验中L选为0.2m,5m,20m)。最大极化距离达20m;作为对照,电视卫星通信技术中,极化保持在35786km恒定。概括起来,第一个(输入端的)adaptor中的线极化TE10模给出了模式及光子的态矢(state vector),并转换为右旋及左旋的圆极化TE11模。……总之,此论文的原理比较令人费解。 笔者曾用电邮询问A.Carot(博士生)的导师——德国的G.Nimtz教授,他说该文略加修改后将由《Euro.Phys.Lett.》发表,题目改为“Giant negative group time delay by microwave adaptors”(微波转换器造成的巨大负群时延)。该文不再提自旋反转,因为Nimtz说“I don’t see a spin-flip”。最新的结果是:with a circular waveguide and the adaptors tunneling 50m; the signal speed was 1700c!但Nimtz承认说:“I don’t really understand the cause of the strange and strong effet.” 图14 波导等效为多节级联电路 笔者的观点如下:2012年出现的新的方法,本质上是利用波导的周期性相位变化的特性。我们知道,对波导也可建立分布参数等效电路[17]——根据波导的高通滤波器性质,对TM波导,串联电抗为零时发生截止;对TE波导,并联电纳为零时发生截止;对应的级联等效电路见图14,其中(a)是TM波导的情况,(b) 是TE波导的情况。结合本文前述内容(第2节),很容易理解可由波导获得沿长度方向的相角(Ф)周期性变化以及Ф随频率的周期性变化。正确的理解是Ф随z/λ(或l/λ)而变,因此Ф随波导长度变与Ф随信号频率变在概念上是一致的。此外还要运用波导的不连续性(discontinuity)概念;根据波导理论[17],矩形波导(主模TE10)特性阻抗的算式为 (25) Zc与波长(λ)、频率(f)有关表示其色散性质;取fc/f=0.7,则有Zc=528b/a(Ω);对于Yao的论文,波导Ⅰ、Ⅲ的Zc=249.2Ω,波导Ⅱ的Zc=22.2Ω;这可作为进一步计算时的参考。 另一个思考方向是按照光子晶体(PC)来理解,也较简单易懂。总之要采用周期结构,并努力改变相频特性曲线的规律,从而获得负群时延和负群速。 需要说明的是,用波导作为DUT和用同轴线时一样,要靠测量时间差来确定群速vg;设DUT总长为L,真空时波群通过L的时间为L/c,非真空(真实媒质)时波群通过时间为τg,二者之差表示媒质影响:△t=τg-L/c,故有 (14b) 上式与(14a)式相似,如测出△t即可得vg;另外,如△t<0,则vg<0(得到NGV)。 前面所述及的技术发展已导致文献上出现了一个有趣的词语:负群速传输线(NGV transmission line)。因此,人们会设想采用其他传输线形式以获取负群速(NGV)和负群时延(NGD)。在微波,使用微带线(micro-strip line)会比使用波导更廉价和方便。图15是微带线的示意,其中显示了三个部分。理论与实验表明[21],当f≤4GHz,准静态分析得出的特性阻抗公式是可用的;当导体条较窄(w/d≤1),Zc公式为 (26) 式中Z00是真空中波阻抗(Z00=376.62Ω≅377Ω);对于宽条(w/d>1),Zc公式为 (27) 另外,有的微波工程手册依据下式绘制特性阻抗与w/d的关系曲线,用εr作为可变参数从而绘出曲线族: (28) 这些公式和曲线为实验设计带来了方便。 图15 微带线示意 那么是否可以用多段不同阻抗的微带线级联,经由失配创造出反常色散,从而得到NGV?我们认为有可能成功,因为微带线与同轴线并无本质上的不同(都是双导体导波系统,频率不太高时均可传输TEM波)。不过,在实际中尚无人做过有关实验。……2009年G.Monti和L.Tarricone[3]的工作,是针对超材料(metamaterials)的,也叫左手材料(LHM)或负折射材料(NRI),故其中包含开口环形谐振器(split ring resonator,SRR)。图16表示导体条与SRR耦合连接的情况,图17表示SRR数目对性能的影响(S21是复传输系数,用散射矩阵表示;φ21是S21的相角);实线表示总共6个SRR,虚线表示12个SRR。文献[3]的工作证明当一个Gauss脉冲通过人为设计的传输线系统时,可以产生负群速及负群延时;而维持波形不变是可以做到的。 图16 SRR耦合的微带线示意 图17 SRR数量对性能参数的影响 那么能否不用SRR而简单地用不同阻抗的微带线级联?根据用CPC做实验的经验,每段长约(λ0/6~λ0/4);在微波,若f0=8.2GHz(λ0=3.7cm),要求每段长约为(6~8)mm。但这种设计和实验尚无人做过。 1914年由A.Sommerfeld和L.Brillouin[22]提出的经典电磁波波速理论为人们认识波的规律提供了一个重要的入口,即使在今天对其意义和价值不能完全否定。例如正是这个理论最早给出了NGV的定义,使人们认识到:以群速vg行进的波群,如vg比无限大还大就是负群速(NGV)传播。但SB理论并未使波速问题得到最终的解决,今天我们很容易指出它存在的若干问题。SB理论的第一个错误是在Brillouin图的绘制中否定了负相速(NPV)存在的可能。2000年4月,K.Wynne等[23]报道说,在近场太赫装置中产生了120fs的太赫脉冲,用以研究小尺寸金属圆波导(直径50μm、长40μm)的传播,实验测量频段为0~3THz。由于是截止波导状态(f L.Brillouin对群速的认识也有很大的片面性;例如在1960年著作中不加批评地引述了20世纪早期的一个观点:“Natually,the group velocity has a meaning only as it agrees with the signal velocity.The negative parts of group velocity have no physical meaning”。(见:A.Schuster,《Einführung in die theoretische optik》,Leipzig,1907)。这种说法已被百年后的事实所驳倒——21世纪最初10年当中不断有“群速超光速”和“负群速”实验成功的报道,负群速如无意义就不会有这么多科学家研究。负群速并非缺少物理意义,而是内涵非常丰富。 当然,近年来有的文献在谈到对物理现象的应用时流露出一种矛盾的心态。例如WKD实验[9]发表后美国《Science News》杂志将其评为“2000年物理学10大新闻”之一,但研究者却一再声明“群速不是信息速度”,因此不违反因果性(Causality)。Hache实验[12]发表后,在接受媒体采访时他一方面说,目前科学家已不断在实验室中打破了相对论的速度极限,使光脉冲的传输速度超过了光速;现在实验获得了超光速电脉冲,证明光波的规律同样适用于电波;研究成果有助于提高计算机运行速度和远程通信速度。同时又说,能量传输速度并未超光速;而且信号传输速度越快失真越严重,因而从理论上讲尚无法以超光速传输有用信息。……这种矛盾的态度在最近有了改变,例如著名刊物《Phys.Rev.Lett.》在2011年刊出的某论文[5],写出了前所未有的坚定的话语:“Our experiments show that the group velocity of the signal pulse does exceedc,this scheme provides a simple platform for studying superluminal light physics,and provides a new way of opening up superluminal communications via optial fibers”。可以说,随着时间的推移,科学家们对实现超光速通信的期望和信心都在增加。 信息能否以超光速传送当然是人们最关心的问题,以下我们作深入分析。“群速不是信息速度”的说法最早见于Brillouin的1960年著作,原话讲的不是信息速度而是信号速度,是为了声明“The signal velocity is always less than (or at most equal to) the velocity of light in vacuum”。信号速度定义的依据是:“The arrival of the signal can be arbitrarily defined as the moment when the path of integration reaches the polef0”,亦即“信号到达时间可人为地定义为积分路径到达极点jω0的时间”。分析和计算的结果见图18,其中vs是信号速度(为了比较用虚线绘出了群速vg)。总之Brillouin的结果是,在远离ω0附近的区域vs与vg相同,ω0在附近v≠vg;由于c/vs>1,vs 图18 Brillouin图的部分示意 笔者认为这一分析存在问题;首先,定义是纯数学的而非物理的,与人们心目中的信号速度(信息传送的快慢)概念并不符合。事实上没有必要把定义抽象化、数学化;对照信息时代的实践,传送信息的方式是用已调波(modulated waves),即把有用信息用波包的方式(通常频率较低)调制在载波(通常频率较高)之上,并作整体性的输运。人们日常生活所用的收音机、电视机都是如此,因此根本问题在于整个波群的传输,而波包在传送过程中不发生失真才是基本的要求。这意味着调制信号(波包)的形状不随传播时间(t)和空间(z)而变。做到这一点才能保证信息的传输正常化,即不发生错误和缺失。群速在本质上是波包的相速;相对论学者也承认“在波包不变形(不失真)的条件下群速是信号速度”[24 ];况且我们也没有别的更好的定义来描写一个波群(例如一个光脉冲)的运动速度。因此,矛盾聚焦到“波包不失真”这一点上。如做不到不失真,群速也缺乏清晰的物理意义。总之,没有必要寻找看似严谨但却脱离实际的信号速度(或信息速度)定义,注意力要放在波形不变化上;如做得好,群速就是人们关注的信号速度。 因此我们再做一些基本的分析;首先,用ej(ωt-kz)表示一个沿z向传播的行波,并把波矢的模值k按Taylor级数展开: (ω-ω0)2+…… (29) 当ω与基值ω0的差为小量,则可只取两项,故有 ωt-kz=ωt-k(ω0)z-k′(ω0)·(ω-ω0)z (30) 因而 exp[j(ωt-kz)]=exp{j(ω-ω0)[t-k′(ω0)z]}·expj[ω0t-k(ω0)z] (31) 等式右端后者为频率ω0的载波,前者代表包络(波包)。取t-k′(ω0)z=const.,微分后可得包络的相速(即整个波群的速度,群速): (32) 以上讨论的基础是(ω-ω0)为小量,即群速定义适用于中心频率ω0附近的窄频带中。另外,vg=dz/dt的使用表明速度基本定义的普适性,不能说“Newton经典力学不适用于波科学”。 当波群从z=0处传输到z=l处,中间过程无非是遭遇振幅衰减和相位变化。假定波群中各单色波处于△ω=ω1-ω2频域,则规定电场强度为Ez(z,t)时就有 α(ω)≅α(ω0) (33) (34) 这时就可写出 (35) Ez(l,t)= (36) (34)式即相频特性方程β(ω),可写作: β(ω)≅[β(ω)-ω0vg]+vgω (37) 令β(ω0)-ω0vg=a,则有 β(ω)≅a+vgω (37a) 至于群速与能量传播速度(能速ve)的关系,在这方面存在两种极端的看法。19世纪后期,Lord Rayleigh很重视群速,认为“群速代表能量速度”,今天来看这观点并不全对亦不全错。然而近年来有相对论学者强调“群速不代表能量传送速度”,以此贬低群速的意义,又否定群速为负的可能,是走向另一极端。至于SB理论,认为全频域均有ve (38) (39) 这表示只要群速足够大,能速超光速是可能的!这也说明提高群速是有意义的,亦即研究“群速超光速”问题是有意义的。在今天,群速仍具有基础性和重要性。 在国际上“群速超光速”实验虽有不少,其结果常常是vg/c<10;这样的“小超光速”条件,能速一般是亚光速。假定|T|=10-1~10-3,故|T|-2=102~106,可见只有vg是c的百倍乃至百万倍时,能速才可能是超光速的。这种“大超光速”似乎只发生在某些特定条件下,例如引力传播速度[26-28],挠场传播速度[29],量子纠缠态传播速度[30]。 因此我们可以得出以下几点结论:①群速是波群传输过程的最重要参数之一;既然信息是调制在载波之上的波包,绝不能说波群(例如光脉冲)到达了信息却未到达。贬低群速的意义是错误的,简单化地讲“群速不是信息速度”是不妥的。②只要vg、ng在频带△ω中不变化,信号传输不失真条件就得到满足,群速代表信号(以及信息)传送的快慢这一点就不成问题,群速自身定义也更具可靠性。③群速超光速的实验结果,如vg/c足够大,能量传送速度亦可能超光速。④既然负群速比任何正群速(包括无限大速度)都大,从逻辑上讲凡是实现了负群速的实验结果都实现了信息速度超光速。 对于以上各点,最后一条或许会引起争议。其实这与“负温度”概念是相似的。在2009年出版的《大百科全书·物理学》[31]中指出:“负温度状态比正温度状态更热;负温度比正温度要高”;既如此,“负速度比任何正速度更快”也就不难理解了。重要之点在于要看到近年来对负群速及负群时延的实验研究已扩大到宽广的频域,低端可为短波及更低频率,高端可为微波乃至光频。实验既可用增益媒质完成,又可仅靠无源媒质而实现。实验结果往往呈现出共同的规律,无论对超光速研究或物理学中的负参数探索都带来丰富的启迪。 对负群速及负群时延的研究已有漫长历史——如从1914年A.Sommerfeld和L.Brillouin[22]提出经典波速理论算起,至今已将近百年。如从1907年A.Einstein[32]发表否定负速度和超光速信号速度可能性的论文算起,则已超过百年。多年来人们从理论上和实验上作了许多新的研究,其结果不仅证明负群速和负群时延存在,确定了负群速是比超光速群速还要快的波速度。不仅如此,我们的分析表明超光速通信(即信息速度vs>c)不但可能,或许它是在某些负群速实验中已经实现的现实。 2012年9月19日美国《Time》周刊网站称[33]:“NASA actually working on faster-than-light warp drive”( 9月21日中国《参考消息》报刊出时题为“NASA 着手研究超光速曲速引擎”)。这表示美国航天局已经安排专家在研究超光速宇宙航行的问题,证明笔者过去发表的观点是正确的。这就给了我们精神上的鼓舞和科学上的期望。 [1]Gehring G M.Observation of backward pulse propagation through a medium with a negative group velocity[J].Science,2006,312(12 May): 895-897. [2]Xiang Y.Photon tunneling in a frustrated total internal reflection structure with a lossy indefinite metamaterial barrier[J].Appl Phys A,2007,87: 251-257. [3]Monti G,Tarricone L.Negative group velocity in a split ring resonator-coupled microstrip line[J].Prog EM Res,2009,94: 33-47. [4]Choi H.Bandwidth enhancement of an analog feedback amplifier by employing a negative group delay circuit[J].Prog EM Res,2010,105: 253-272. [5]Zhang L.Superluminal propagation at negative group velocity in optical fibers based on Brillouin lasing oscillation[J].Phys Rev Lett,2011,107: 093903 1-5. [6]Yao H Y,Chang T H.Experimental and theoretical studies of a broadband superluminality in Fabry-Perot interferometer[J].Prog EM Res,2012,122: 1-13. [7]Carot A,Aichmann H,Nimtz G.Negative group velocity and spin-flip in microwave adaptors[J].Submitted 4 May 2012,http://arXiv: org/abs/1205.1000.also: Giant negative group time delay by microwave adaptors[J].Euro Phys Lett,2012,96(6):64002 1-4. [8]Glasser R T.Stimulated generation of superluminal light pulses via four-wave mixing [J].arXiv: 1204.0810vl [quant.ph],3 Apr 2012,1-5. [9]Wang L J,Kuzmich A,Dogariu A.Gain-asisted superluminal light propagation[J].Nature,2000,406: 277-279. [10]黄志洵.负波速研究进展[J].前沿科学,2012,6(4):46-66. [11]Mitchell M W,Chiao R Y.Causality and negative group delays in a simple bandpass amplifier[J].Am Jour,1998,66: 14-19. [12]Hachè A,Poirier L.Long range superluminal pulse propagation in coaxial photonic crystal[J].Appl Phys Lett,2002,80(3): 518-520. [13]Munday J N,Robertson W M.Negative group velocity pulse tunneling through a coaxial photonic crystal[J].Appl Phys Lett,2002,81(11): 2127-2129. [14]黄志洵.论电磁波传播中的负速度[J].中国传媒大学学报(自然科学版),2007,14(1): 1-11. [15]Huang Z X,Lu G Z,Guan J.Superluminal and negative group velocity in the electromagnetic wave propagation[J].Eng Sci,2003,1(2): 35-39.又见:Lu G Z,Huang Z X,Guan J.Study on the superluminal group velocity in a coaxial photonic crystal[J].Eng Sci,2004,2(2): 67-69. [16]周渭,李智奇.电领域群速超光速的特性实验[J].北京石油化工学院学报,2009,17(3): 48-53. [17]黄志洵.波导截止现象的量子类比[J].电子科学学刊,1985,7(3):232-237;又见:黄志洵.截止波导理论导论[M].第2版.北京:中国计量出版社,1991. [18]Enders A,Nimtz G.On superluminal barrier trasversal[J].Jour Phys I France,1992,(2): 1693-1698;又见:Nimtz G Heitmann W.Superluminal photonic tunneling and quantum electronics[J].Prog Quant Electr,1997,21(2): 81-108. [19]Pablo A.Propagation speed of evanescent modes[J].Phys Rev E,2000,62(6): 8628-8635. [20]Winful H G.Group delay,stored energy,and the tunneling of evanescent electromagnetic waves[J].Phys Rev E,2003,68: 016615 1-9. [21]黄志洵,王晓金.微波传输线理论与实用技术[M].北京:科学出版社,1996. [22]Sommerfeld A.Uber die fortpflanzung des lichtes in dispergierenden medien[J].Ann d Phys 1914,44(1): 177-182.又见:Brillouin L.Uber die fortpflanzung des lichtes in dispergierenden medien[J].Ann d Phys,1914,44(1): 203-208.also: Brillouin L.Wave propagation and group velocity[M].New York: Academic Press,1960. [23]Wynne K.Tunneling of single cycle terahertz pulse through waveguides[J].Optics communication,2000,176: 429-435. [24]张元仲.反常色散介质‘超光速’现象研究的新进展[J].物理,2001,30(8):456-460. [25]Aguanno G D.Group velocity,energy velocity,and superluminal propagation in finite photonic band-gap structure[J].Phys Rev E,2001,036610 1-5. [26]Eddington A E.Space,time and gravitation[M].Cambridge: Cambridge Univ Press,1920. [27]Flandern T.The speed of gravity: what the experiments say[J].Met Research Bulletin,1997,6(4): 1-10 ;又见:Flandern T.The speed of gravity: what the experiments say[J].Phys Lett 1998,A250: 1-11. [28]黄志洵.引力传播速度研究及有关科学问题[J].中国传媒大学学报(自然科学版),2007,14(3): 1-12. [29]雷锦志,江兴流.电化学异常现象与挠场理论[J].科技导报,2000,6: 3-5. [30]Gisin N.Optical test of quantum nonlocality: from EPR-Bell tests towards experiments with moving observers[J].Ann Phys,2000,9: 831-841.又见:Salart D.Testing the speed of ‘spooky’ action at a distance[J].Nature,2008,454(Aug 14): 861-864. [31]中国大百科全书——物理学[M].北京:中国大百科全书出版社,2009,154. [32]Einstein A.The relativity principle and it’s conclusion[J].Jahr.Der Radioaktivit und Elektronik,1907,4: 411-462 ;中译:关于相对性原理和由此得出的结论[A].范岱年,赵中立,许良英译.爱因斯坦文集·第2卷[C].北京:商务印书馆,1983.150-209. [33]NASA actually working on faster-than-light warp drive.http:// techland.time.com,2012.09.19. AbnormalEM-wavesPropagationinPassiveMedia HUANG Zhi-xun (Information Engineering School,Communication University of China,Beijing 100024) Recently,there has been interest in modifying the group velocity of optical pulses,resulting in stopped,slow,and fast (superluminal)light.According to the physical theory,“fast light” appears in the anomalous dispersion medium,and then it so called “fast light medium”.There are many experimeuts to produce fast light,this situation opens up new perspectives for the so called “dispersion engineering”.For example,signal propagating with a group velocity that exceeds the speed of light in vacuum(c) is intriguing for scientists.And then,the traveling of short wave pulses,microwave pulses and light pulses with group velocityvg,whose values exceed infinity,so called negative group velocity(NGV) propagation.Such circumstance occurs when the peak of a pulse traveling through DUT,exits before the peak of the input pulse has reached the beginning of DUT.This effect is counterintuitive,but it is a discover under the experimental basis.When the group velocity of light in a material is negative,it is the NGV medium. The definition of signal velocity by Brillouin,mathemalical meaning exceeds physical meaning.We argue that undistorted wave group(wave packet) propagation are the first consideration.According to this viewpoint,the theoretical analysis show that superluminal propagation (i.e.superluminal communication) was observed by authors of many NGV researchers.……The superluminal group velocity wave propagation,the negative group velocity wave propagation——each of the two cases has its own use.Now,scientists do research works in these fields: such as optical communication,squeezed light and quantum entanglement.The condusion tell us that,a hight efficiency and low-loss fast light scheme may explore potential applications. negative group delay time; negative group velocity; passive medium; fast light 2012-11-12 黄志洵(1936-),男(汉族),北京市人,中国传媒大学教授、博士生导师,中国科学院电子学研究所客座研究员. O412 A 1673-4793(2013)01-0004-17 (责任编辑:宋金宝)





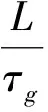
5 使用微带线结构的可能性


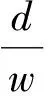



6 实现超光速通信的可能性



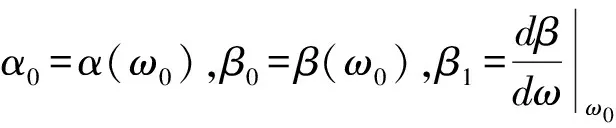




7 结束语