粒子群优化模糊聚类算法在煤气鼓风机组振动故障诊断的应用

赵 欣

(重庆工商大学计算机科学与信息工程学院，重庆400067)

煤气鼓风机组是煤化工厂的重点关键设备，其运行状态是否正常直接关系到焦炉生产的安全和经济运行。由于其设备结构的复杂性和运行环境的特殊性，煤气鼓风机组振动故障率较高，且故障危害性也很大，因此煤气鼓风机组振动状态的监控也越来越受到企业的重视。目前，振动信号的故障诊断大多采用以神经网络、专家系统及模糊聚类算法等智能诊断方法［1-4］。与其他方法相比，模糊技术处理在解决不确定问题上有其特殊的优势，其中最为代表的是FCM模糊聚类算法。但该算法亦存在如下缺点:该算法过分依赖初始中心的选择，若能恰当选择初始中心，则聚类效果好，否则聚类效果将很不理想，甚至会导致无解，且不恰当的初始聚类中心和阈值容易使该算法陷入局部极值而得不到分类。将PSO算法和加权模糊聚类算法相结合，提出一种基于粒子群优化的模糊聚类算法(PSO-WFCM)［5］，该方法利用C均值聚类算法得到的聚类中心作为PSO-WFCM的初始聚类中心，利用WFCM进行加权模糊聚类，然后再利用粒子群(PSO)算法寻找最佳聚类中心。实验结果表明，该算法不仅迭代次数少，而且聚类精确，较大提高了故障诊断的准确率。

1 加权模糊聚类算法

模糊C均值聚类算法(FCM)［6-7］，是由隶属度确定每个数据点属于某个聚类的程度的一种聚类算法。由于FCM算法不考虑不同样本矢量对聚类效果的不同影响，因此提出基于样本加权的FCM算法，即WFCM算法。

假设X={x1，x2，…，xn}为p维实数空间中给定的一个有限样本子集，对于任意给定的类别数c，2≤c≤n，样本集X的加权模糊C均值(WFCM)聚类问题可以表示成如下的数学规划问题:

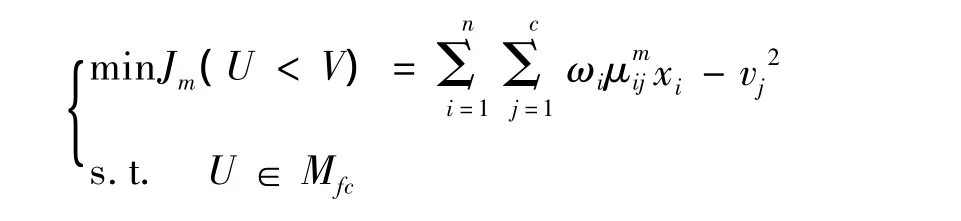
其中，ωi为每个样本的加权系数，且满足概率约束条件=1，U= ［μij］n×c为模糊划分矩阵。

利用拉格朗日乘子法，可以推导出式(1)的优化迭代公式:

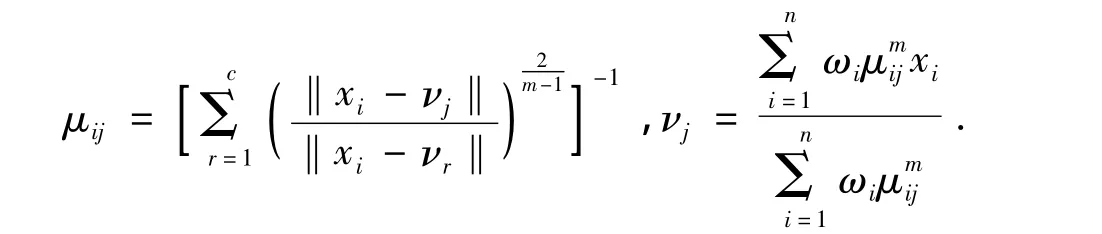
2 粒子群算法

粒子群算法原理:D维空间随机产生一个具有m个粒子数的初始种群，并赋予每个粒子一个随机飞行速度，每个粒子都为优化问题的一个可行解，并由目标函数为之确定一个适应值(fitness value)。其中第i个粒子的位置为=(xi1，xi2，…，xiD)，i=1，2，…，m，其速度=(vi1，vi2，…，viD)。将带入目标函数可计算出其适应值。记第i个粒子搜索到的最优位置为=(pi1，pi2，…，piD)，整个粒子群搜索到的最优位置为，其更新操作如下:

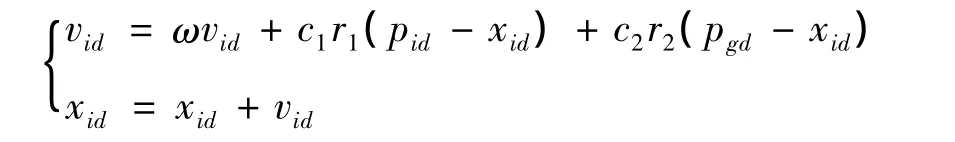
其中，i=1，2，…，n，d=1，2，…D;c1和 c2是加速因子，为正常数;r1和 r2服从［0，1］上的均匀分布随机数;ω为惯性权重函数，公式如下:

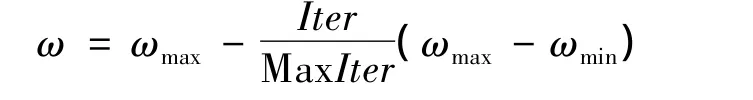
其中，Iter，Max Iter分别是当前迭代步数和最大迭代步数。当达到了设定的最大迭代次数，或粒子群迄今为止搜索到的最优位置满足了设定的最小适应阈值，迭代终止。

计算粒子的适应度值.若当前适应值更优，则令当前适应值为其个体历史最好适应值，并保存当前位置为其个体历史最好位置，对每一个粒子，如果所有粒子的个体历史最好适应值中的最好值好于当前的全局历史最好值，则将该粒子的适应值作为全局历史最好值.即满足:

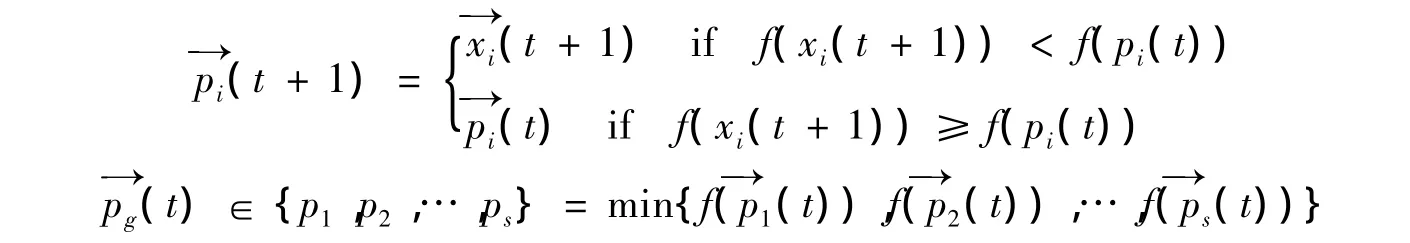
由此可见，粒子群的更新操作包含3个部分，首先是粒子先前的速度，表示对先前速度的一个记忆;其次是粒子的认知部分，是指当前点指向粒子自身最好点的一个方向;第三部分是指当前点指向种群最好点的方向。这三个部分决定了粒子的的空间搜索能力，第一部分可以平衡全局和局部搜索能力，第二部分使粒子具有全局搜索能力，避免局部最小，第三部分实现粒子群体之间的信息共享。

在此提出的基于粒子群优化的加权模糊C均值聚类算法(PSO-WFCM)，可以避免FCM算法陷入局部最优的问题。基本思想是利用C均值聚类算法得到的聚类中心作为 PSO-WFCM的初始聚类中心，用PSO代替FCM算法的梯度下降过程，使算法具有很强的全局搜索能力，避免聚类陷入局部极值。

FCM算法的核心是最佳聚类中心的确定，因此将聚类中pi(i=1，2，…，c)作为PSO算法中的粒子进行编码.对于每个粒子的评价，采用群体适应度方差来描述。设Fi是第i个粒子的适应度，¯F是目前粒子群的平均适应度，σ2为粒子群的群体适应度方差:

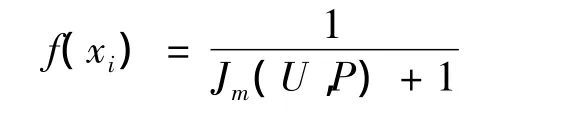
Jm(U，P)为FCM的目标函数值，每个粒子适应度的高低表明了这种聚类中心选取下聚类效果的优劣。

算法步骤如下:

步骤1:读入样本数据，设定聚类数目C和种群规模，每个粒子代表各类的聚类中心，初始化聚类中心，初始化粒子速度和位置信息，设置迭代计数器及迭代次数。

步骤2:根据适应度函数f(xi)，计算每个粒子的适应度值。

步骤3:根据式(1)更新每个粒子新的速度和位置，并限制其不超过边界。

步骤4:根据式(6)更新粒子的个体最佳位置，根据式(7)更新粒子群体最佳位置。

步骤5:如满足迭代终止条件，则算法结束，否则，返回步骤(2)。

3 基于PSO-WFCM的煤气鼓风机组故障诊断

为检验PSO-WFCM算法的聚类有效性，以某钢铁厂的煤气鼓风机组为例将PSO-WFCM与FCM算法进行了诊断比较［8-12］。笔者收集了该厂煤气鼓风机机组8种振动故障的现场试验数据建立故障样本，样本经过预处理且去除噪声，选取其中50组典型数据建立故障样本集，样本维数为8，每维特征分别对应特征频谱0.01f～0.39f、0.40f～0.49f、0.50f、0.51f～0.99f、1.0f、2.0f、3f～5f、＞5f共 8 个频段的幅值，其中 f为工频。用 Y1、Y2、Y3、Y4、Y5、Y6、Y7、Y8 依次代表不平衡、气动力偶、不对中、油膜振动、转子与静摩擦、转子横向裂纹、转子支承系统松动、正常状态8种振动故障类型。表1为2种算法的实验结果比较。将FCM和PSOWFCM分别对样本集进行聚类分析，并找出各故障类型的聚类中心。表1为两种算法的实验结果。表2为优化后的不同频段下的故障聚类中心样本。

表1 两种算法的试验结果

从实验结果可以看出，FCM算法错分样本数很大，聚类结果与实际情况相差较远，PSO-WFCM算法则在收敛速度、诊断正确率、收敛性能方面表现更优，聚类效果显著增强，对机组故障能进行准确有效地辨识与诊断。

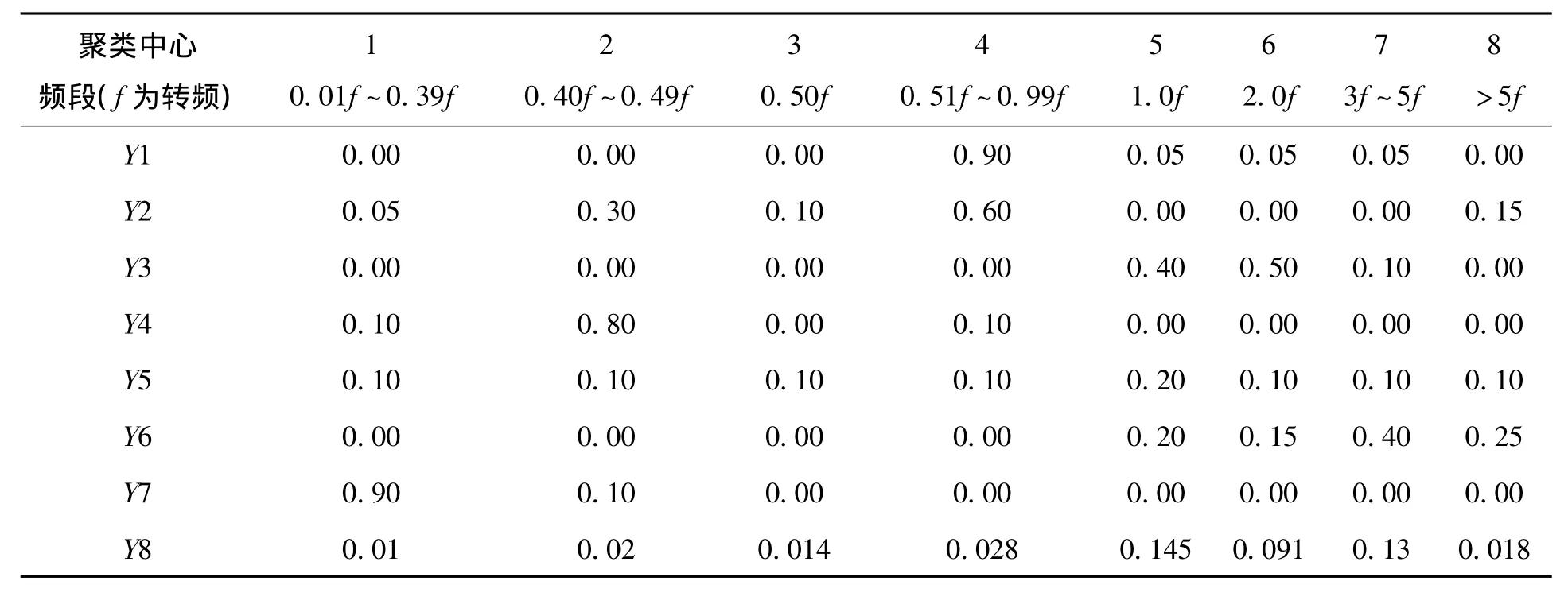
表2 故障聚类中心样本

表3为2个诊断实例的待检故障样本。实例1，汽轮鼓风机组在运行过程中，2瓦、3瓦轴振动超标，对2瓦水平方向采集到的振动频谱进行特征提取并模糊预处理后，得到故障模式x1。实例2，汽轮机经过大修且过了大约1个月后，机组振动异常，相位极不稳定，振动值随转速升高明显加大，振动频谱的主要分量为基频，并带有明显的2f、3f及低频分量。

表3 待检测故障样本

将表3的故障样本x1、x2分别与上述40组标准故障中心(包含表1的8组故障中心样本)一起构成数据集进行聚类分析，故障样本与哪种标准故障中心聚为一类，则说明该故障属于与聚类中心同类的故障，诊断结果如表4所示。

表4 两种算法的诊断结果

对实例1，两种算法诊断结果为:x1与Y3聚为一类，表明该故障属于Y3故障模式，即机组发生了不对中故障，与现场检查结果一致。对实例2，PSO-WFCM诊断结果:x2既属于Y3故障，又属于Y7故障，与现场实际结果相符。FCM诊断结果为x2与Y7聚为一类，其余各中心聚为一类，表明该故障模式属于Y7的故障，即转子支承系统松动故障，与实际结果不符。通过2个诊断实例表明，PSO-WFCM算法比FCM算法诊断更准确。

4 结论

针对FCM算法中聚类结果对初始中心敏感的特性，本文提出的PSO-WFCM算法通过粒子群的迭代搜索达到最优解，具有较强的全局搜索能力，提高了聚类的效果，应用在煤气鼓风机组振动故障诊断中，能充分利用不同倍频下振动数据的属性特征，提高了故障诊断的正确率。

［1］李佳，礼宾，王梦卿.基于神经网络的齿轮故障诊断专家系统［J］.机械传动，2007，31(5):81-83

［2］温重伟，李荣钧.改进的粒子群优化模糊C均值聚类算法［J］.计算机应用研究，2010，27(7):2520-2522

［3］成淼.加权模糊C均值算法在图像分割中的应用［J］.科技信息，2011(5):564-583

［4］石丁丁，潘宏侠.蚁群算法在电机故障诊断中的应用［J］.大电机技术，2009(1):26-30

［5］李飞，夏士雄，牛强.基于改进粒子群优化聚类算法的故障诊断方法［J］.微电子学与计算机，2010，27(8):82-85

［6］ABDEL K，REHAB.Genetically improved PSO algorithm for efficient data clustering［J］.Machine Learning and Computing(ICMLC)，2010 Second International Conference on，2010(2):71-75

［7］BALAFAR M A，RAMLI A R，MASHOHOR S.etal.Compare different spatial based fuzzy-C_mean(FCM)extensions for MRI image segmentation［J］.Computer and Automation Engineering(ICCAE)，2010 The 2nd International Conference on，26-28 Feb.2010:609-611

［8］左爱武.煤气鼓风机振动故障频谱分析［J］.冶金动力，2009(4):43-44

［9］LI A，GU Q，FENG G C，et al.SNN-A neural network based combination of software reliability growth models.2009 1st International Conference on Information Science and Engineering，2009:5109-5112

［10］LGWE P，EMRANI M，ADEEB S，et al.Assessing torso deformity in scoliosis using Self-Organizing Neural Networks(SNN).Ferroelectrics，1994(157):287-292

［11］ALLEN J，NHASAN S B，HODA S，et al.A low-power haar-wavelet preprocessing approach for a SNN olfactory system［C］.Proceedings-IDT＇07 The 2nd International Design and Test Workshop，2007:222-225

［12］胡芳霞，谢志江，岳茂雄.混沌粒子群优化模糊聚类的旋转机械故障诊断［J］.重庆大学学报:自然科学版，2011，34(6):26-30

［13］周荣，孟琦.一种ASON网络的基于业务动态变化的p-cycle保护算法［J］.四川兵工学报，2011，32(1):120-123