基于fluent软件对海绵钛反应器内部温度场的模拟
2013-10-31陈德明谢丽娟陈映志马艳琴
张 静,陈德明,谢丽娟,陈映志,马艳琴
(攀枝花钢企欣宇化工有限公司,四川 攀枝花 617064)
0 引言
目前,海绵钛生产企业主要采用镁热法(Kroll法)生产海绵钛,主要过程是用镁还原TiCl4制取金属钛,包括还原工序与蒸馏工序,其中还原工序是关键环节[1]。镁还原TiCl4的反应是一个强烈的放热反应,如不及时排出反应器内的余热,将使反应器内的温度急剧升高,造成三方面影响:①导致Fe及其他杂质元素渗入海绵钛中(如在1085℃时,Fe与Ti可形成Fe-Ti合金),从而降低海绵钛品级;②不利于后续的蒸馏工艺,易形成硬心,降低海绵钛产品的正品率(攀枝花钢企欣宇化工有限公司钛业分公司2012年1—3月生产的海绵钛质量情况统计表明,单炉海绵钛正品的平均比例为66.7%,而硬心的平均比例为9.0%);③导致大量的镁气化,致使反应器内压力过高,只能通过降低料速的方法进行调节,然而降低料速会造成生产效率降低,生产成本提高。
为了控制还原反应器内的温度,需要分析和研究反应器内温度场的分布情况。本实验采用fluent软件对Kroll法生产海绵钛的反应器内的温度场进行模拟,探索工艺参数对温度场分布的影响规律,寻找工艺改进的方向。
1 模型的建立
1.1 模型假设
计算过程中,假设如下条件成立。
(1)反应器内部的液体部分为连续介质,且所有物性参数在任何部位均一致。
(2)镁还原TiCl4的过程是一个复杂的过程,不仅能生成单质钛,还会生成三价钛及二价钛,为了简化模型,假设反应器内部仅发生如下还原反应:
TiCl4+2Mg=Ti+2MgCl2
(3)加入的TiCl4在液面上方空间完全气化,还原反应仅发生气液反应,且反应均匀地在液面整个表面上进行,反应液面作为还原过程中的热源。
1.2 数学方程
对于fluent软件,求解的能量方程[2]为:
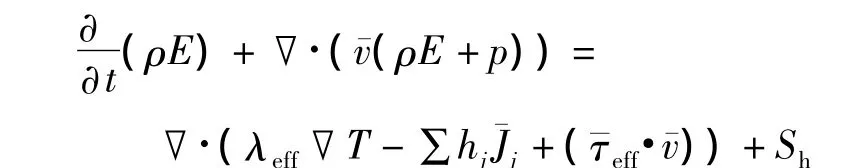
式中:t为时间,s;ρ为密度,kg/m3;E为能量,J;¯为流体运动速度,m/s;p为压力,Pa;λeff为有效导热系数,W/(m·K);T为温度,K;hj为组分j的焓,J;为组分j的扩散通量,mol/(m2·s),为有效粘性耗散系数,与应力张力有关,Pa;方程式右边表示由热传导、组分扩散、粘性耗散而引起的能量转移;Sh包含化学反应放(吸)热以及其他形式定义的体积热源。
本实验中反应器为圆柱形,物理参量根据中心轴对称,因此可选用二维柱状坐标来建立反应器内的数学模型,其热量微分方程的形式[3]可写为:
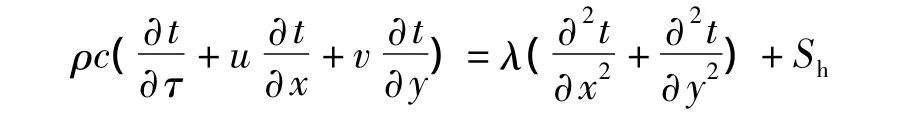
式中:ρ为密度,kg/m3;c为比热容,J·kg/K;t为温度,K;τ为时间,s;x,y分别为二维空间的两个方向;u为物质在x方向上运动速度,m/s;v为物质在y方向上的运动速度,m/s;λ为导热系数,W/(m·K),Sh为由化学反应产生的热源。本文中为简化模型,热源的位置为液面,其能量根据化学反应产生的热流密度进行表征。
1.3 基本物性参数
本实验对反应器内混合液体的基本物性参数进行了一定的简化。密度与粘度通过简单混合定律进行计算,分别如下式所示。
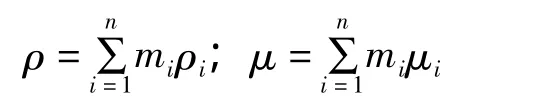
式中:mi为各组分液体的质量分数,ρi与ρ分别为组分i及混合液体的密度,kg/m3;μi与μ分别为组分i及混合液体的粘度,Pa·s。
在还原反应器内,液体的主要组分为原料液镁、还原反应生成的氯化镁以及钛颗粒,在高温状况下,氯化镁的热导率(5 W/(m·K))和钛颗粒的热导率(8 W/(m·K))均明显低于液镁的热导率(97.33 W/(m·K))[4]。因此,采用液镁的热导率代表反应器内液体的热导率。
1.4 几何模型与边界条件
5 t炉反应器内部流体的几何模型如图1所示,为1.8 m×0.4 m的长方形计算区域。长方形底部中心作为坐标的原点,垂直于底面方向为坐标y。计算区域划分为360×180的交错网格。在图1中,长方形上部边界为液面表面,两边边界为反应器壁,底部边界为液体面积的一个截面。
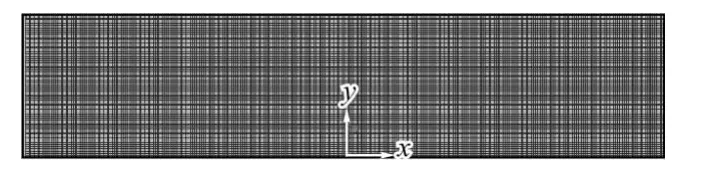
图1 反应器内模型的网格划分Fig.1 Mesh of the model related to reactor
在反应液面处,必须给定整个反应器内的热源参数等相关条件,具体包括初始温度、由化学反应释放出来的热量(热流密度)等。在长方形计算区域边壁上需根据其散热条件分别设置热损失通量,同样在计算域底部边界需根据现场生产状况设置其温度条件。
1.5 散热机理
反应器散热主要是器壁通过空气对流以及辐射散热使反应的余热排出。因此,器壁单位时间散发出的热量为对流传热及辐射传热功率的总和,其关系式如下。
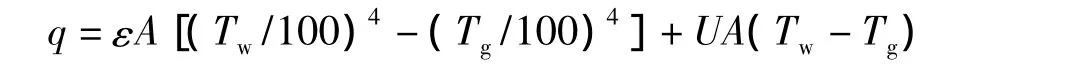
式中:q为对流传热功率及辐射传热功率的总和,W;ε为辐射系数,W/(m2·K4);A为散热面积,m2;Tw为器壁温度,K;Tg为空气室温温度,K;U为对流系数,W/(m2·K)。
1.6 热源设置
还原过程中,反应器内热量主要来源于镁还原TiCl4产生的反应热,其主要化学反应是气化的TiCl4与液态镁在液面反应,主要反应式为:
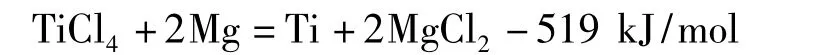
还原过程中该反应连续进行,并假设反应液面为热源位置,根据加料速度的不同,设置不同的热流密度,加料速度为260、300、350、400 kg/h时,设置热流密度为63270、72306、84357、96408 W/m2。
2 结果与分析
2.1 绝热条件下的温度场分布
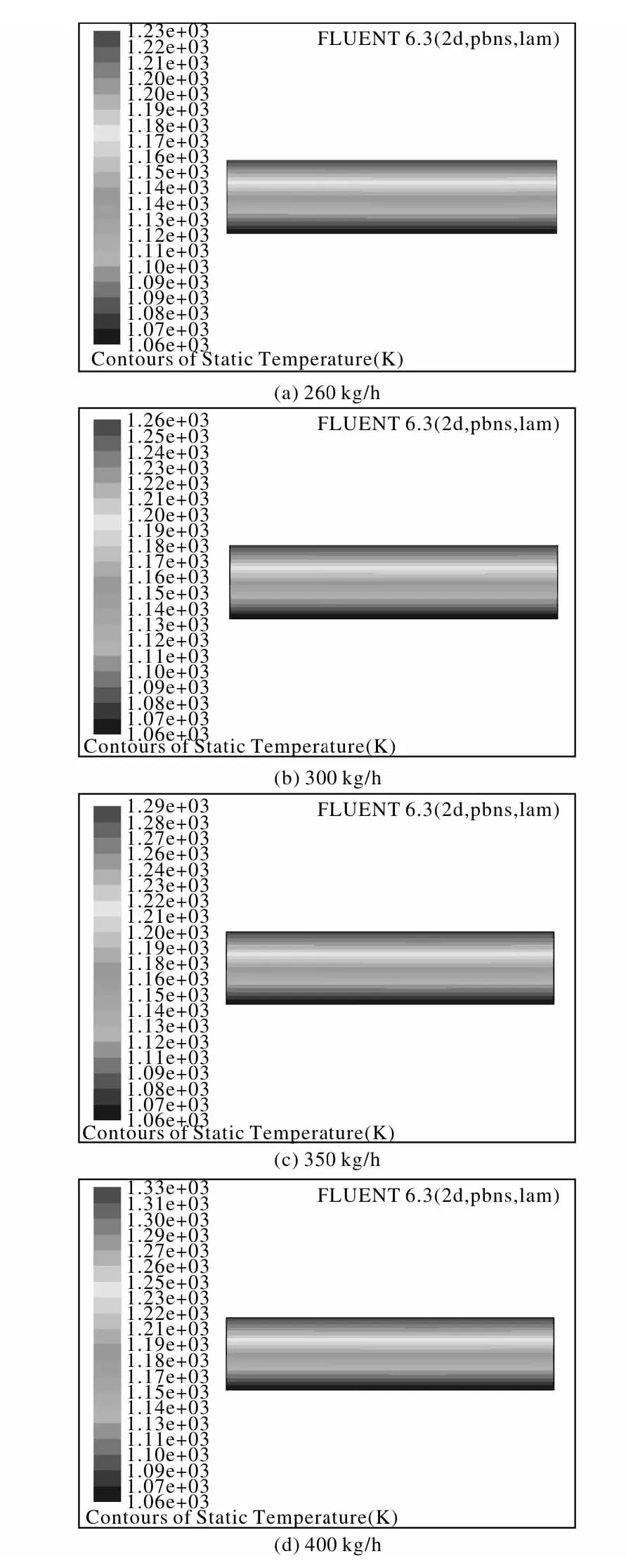
图2 不同加料速度下反应器内温度场的模拟结果Fig.2 The simulation results of temperature field in reactor with different feeding speeds

表1 绝热条件下不同加料速度对应的液面温度Table 1 Temperature of liquid surface in adiabatic condition with different feeding speeds
假设了TiCl4全部气化的情况,反应器内温度场分布如图2所示,具体数据见表1。该模拟结果为开始反应1 h后的温度场分布。从表1可知,随着加料速度的增大,1 h后反应器内的温度升高。在加料速度为400 kg/h时,反应器内的温度比加料速度为260 kg/h时高100℃。由此可知,如果长时间反应会导致反应器内的温度急剧升高,造成超温。为了控制反应器内的温度,将反应过程中的余热排出,需要对反应器进行散热。
2.2 自然风冷条件下的温度场
通过对模型的简化以及物性参数、边界条件的设定,对攀枝花钢企欣宇化工有限公司还蒸车间(反应中期加料速度为260 kg/h)反应器内液体的温度场分布进行模拟,结果见图3。从模拟结果可以看出,在加料速度为260 kg/h时,反应器中心温度为1220 K,反应器壁温度在1040 K左右,与现场所测温度(1019~1039 K)相近,可见该模型可行。
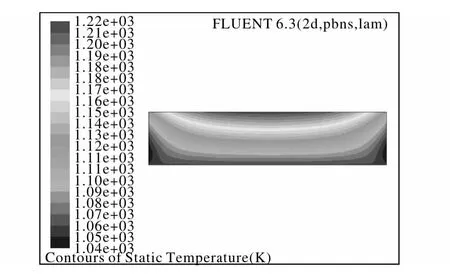
图3 加料速度为260 kg/h时反应器内温度场的模拟结果Fig.3 The simulation result of temperature field in reactor with feeding speed of 260 kg/h
利用该模型对自然风冷条件下,不同加料速度下反应器内部温度场的分布进行模拟。图4为加料速度分别为300、350、400 kg/h时反应器内部温度场模拟的分布情况,具体数据见表2。由图3、图4及表2可以看出,随着加料速度的增加,中心温度与器壁温度均呈现升高的趋势,器壁温度的增幅不大。然而,反应器中心温度随着加料速度的增大,温度由1220 K增至1320 K。可见,加料速度增大后,中心温度急剧升高,极易造成反应器内的温度超温。为获得较好的海绵钛质量及较高的正品率,则需要加大反应器的散热能力,一般可采用强制风冷进行散热。
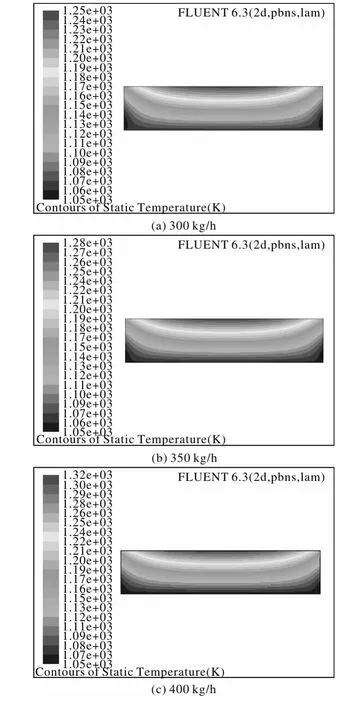
图4 不同加料速度下反应器内温度场的模拟结果Fig.4 The simulation results of temperature field in reactor with different feeding speeds
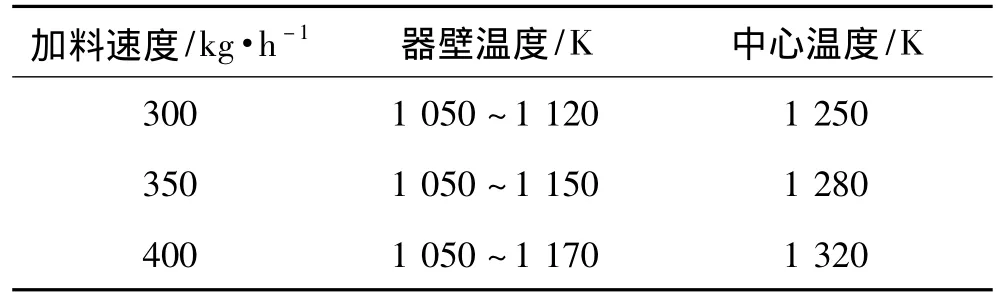
表2 不同加料速度下温度场模拟表征值Table 2 Temperature field characterization with different feeding speeds
2.3 强制风冷条件下的温度场
图5为强制风冷条件下,加料速度为300、350、400 kg/h时的温度场分布。从图中可以看出,提高加料速度后,在强制风冷条件下,反应器内的温度与自然通风条件下加料速度为260 kg/h时的温度场(图3)相近,反应器内的温度有明显的下降。由此可知,采用强制风冷进行散热,可有效对反应器内的温度进行控制。
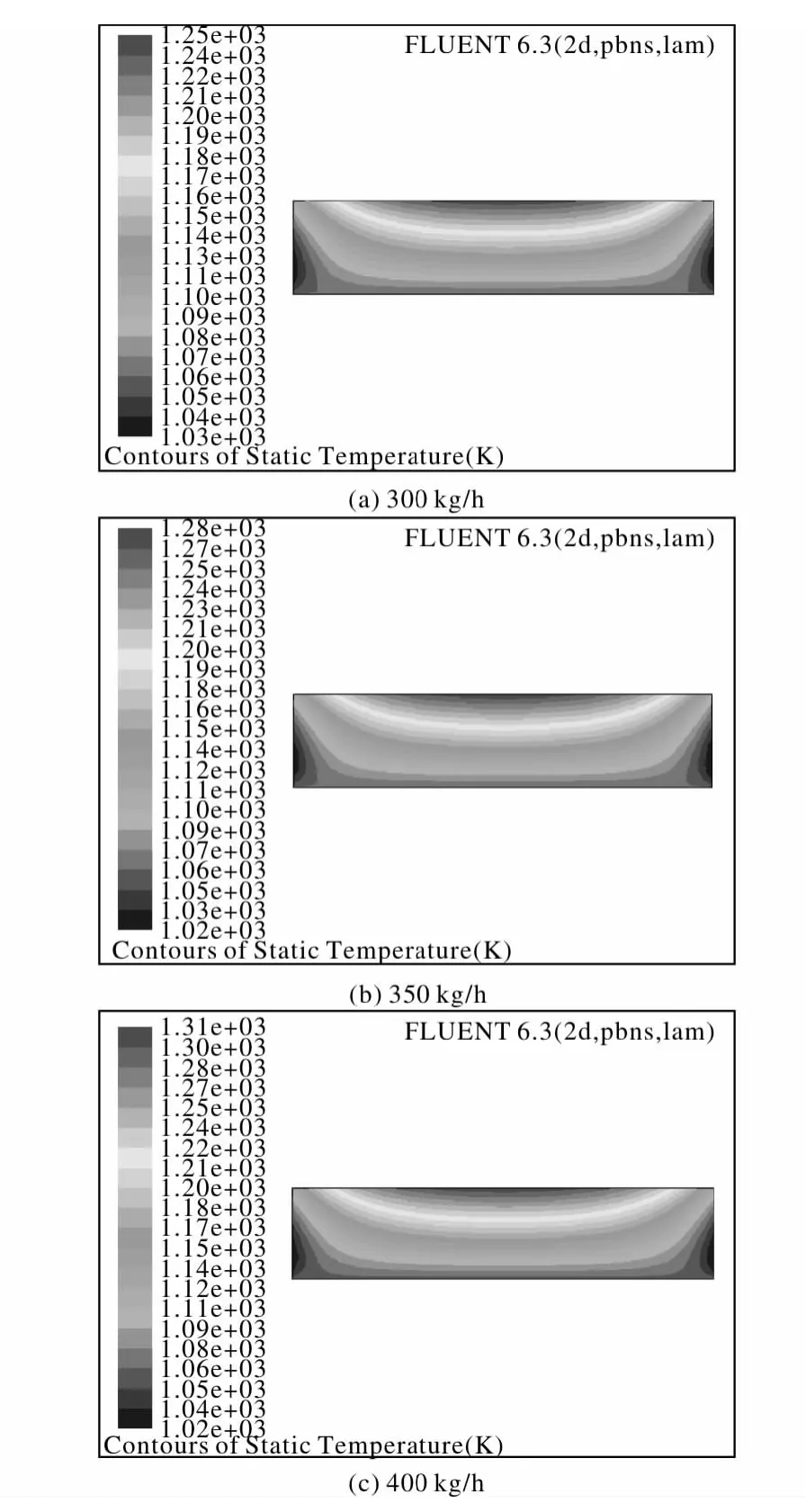
图5 不同加料速度下反应器内温度场的模拟结果Fig.5 The simulation results of temperature field in ractor with different feeding speeds
2.4 加料速度与风量的计算
根据对流传热系数经验公式,强制对流传热系数与流速、换热面积、流体粘度、导热系数、密度、比热容及浮升力相关,对于低粘度流体如空气,通常采用下式计算对流传热系数[7]。
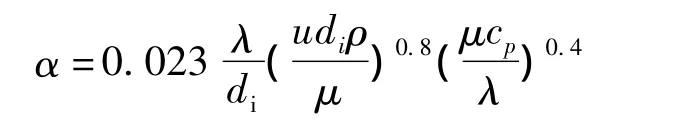
式中,α为传热系数,W/(m2·K);λ为热导率,W/(m·K);d为流体的空间距离,m;u为风速,m/s;μ为粘度,Pa·s;ρ为密度,kg/m3;cp为定压比热容,J·kg/K。
本实验中,由于在强制风冷情况下,采用的流体介质仍为空气,热导率、粘度、空气密度、定压比热容等参数均相同,因此传热系数仅与风速相关。于是对流传热系数公式可简化为:
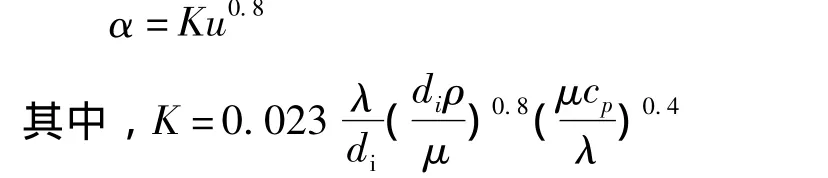
假设进口温度为环境温度(25℃),出口温度通过实测,约为75℃。根据流体力学原理,由温度差造成的风速可采用下式计算。
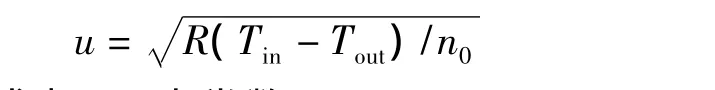
式中:R为常数,8.314 J/mol·K;Tin为入口温度,K;Tout为出口温度,K;n0为空气的单位摩尔质量,kg/mol。
目前,由于使用的还原设备相同,因此通风口的直径及长度为定值,炉壁与反应器壁之间的距离亦为定值,所以不同加料速度下风速的比值与风量的比值应成正比。根据现有还蒸炉通风尺寸、进出口温度等可计算出强制通风条件下的通风量,如表3所示,表中的相对风速为4种加料速度下所需的风速与加料速度为260 kg/h时所需风速的比。
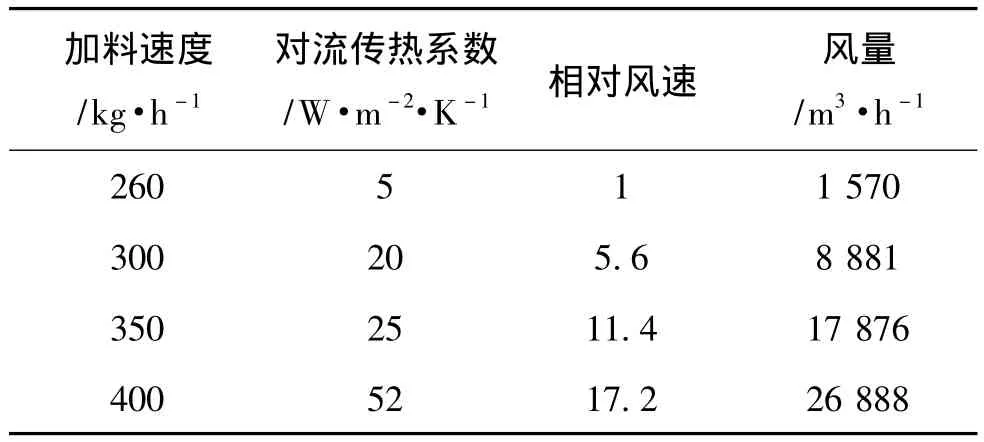
表3 强制风冷条件下的相对风速及风量Table 3 Relative velocity and air volume in forced air cooling condition
根据表3所得数据进行拟合,在加料速度高于260 kg/h时,加料速度与通风量之间的关系,可用下式表示。
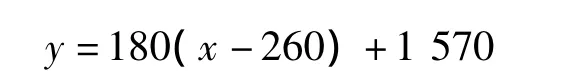
此式示出了通风量(y)与加料速度(x)的数值关系,表明加料速度每提高1 kg/h时,需增加通风量180 m3/h,这对工艺的设计具有一定的指导作用。
3 结论
利用fluent软件对海绵钛还原过程中,反应器内的温度场进行了模拟,得到以下结论。
(1)在绝热条件下,随着加料速度的增大,反应器内温度升高。加料速度为400 kg/h时,反应器内的温度比加料速度为260 kg/h时提高100℃。
(2)在自然风冷条件下,反应器中心温度随着加料速度的增大而提高。在加料速度为260 kg/h条件下,反应器中心温度为1220 K,在加料速度为400 kg/h条件下,反应器中心温度为1320 K。
(3)在强制风冷条件下,加料速度为300、350、400 kg/h时温度场分布与自然风冷条件下加料速度为260 kg/h时的相近,表明通过强制风冷可对反应器内温度进行有效控制,并且加料速度与所需的风量的数值关系可表示为:y=180(x-260)+1570。
[1]狄伟伟,刘正红,孙虎民.镁还原四氯化钛生产海绵钛过程传热分析[J].钛工业进展,2011,28(1):25-29.
[2]FLUENT公司.FLUENT软件应用手册[M].广州:广东旅游出版社,2003.
[3]岑可法,樊建人.燃烧流体力学[M].北京:水利电力出版社,1991.
[4]李金泽.降低海绵钛钛坨上部杂质铁含量的探讨与实践[J].湖南有色金属,2011,27(3):28-29,70.
[5]李鸿斌.还原加料对海绵钛结构的影响及改善措施[J].钛工业进展,2002,19(5):39-41.
[6]蒋维钧,戴猷元,顾惠君.化工原理[M].北京:清华大学出版社,1992.
[7]陈绍波,文江宁,欧阳全胜.海绵钛反应釜内部热场变化的计算机模拟[J].湖南有色金属,2012,28(1):25-26,78.
