粒子群优化算法惯性权重的一种动态调整策略

罗金炎

(闽江学院数学系，福建福州 350108)

粒子群算法(PSO)是Kennedy和Eberhart于1995年提出的一种群体智能演化算法［1］，它源于对简化社会模型的模拟.与其他进化寻优算法相类似，PSO算法也是通过个体间的协作与竞争，实现多维空间中最优解的搜索.它首先生成初始种群，即在可行解空间中随机初始化一群粒子，每个粒子都为寻优问题的一个可行解，并用某个函数计算出相应的适应值，以确定是否达到寻优目标.每个粒子将在解空间中运动，并由一个矢量决定其运动方向和位移.通常粒子将追随当前已知的最优位置，并经逐代搜索，最后得到最优解.在每一进化中，粒子将跟踪两个目标位置，一为粒子本身迄今找到的最优解，代表该粒子自身对寻优方向的认知水平;另一为全种群迄今找到的最优解，代表社会认知水平.粒子群算法已被广泛应用于各种优化问题中，如神经网络训练、调度问题、组合优化等.

为改善粒子群算法的搜索性能，Shi和Eberhart对基本PSO算法进行了改进，在粒子的速度进化方程中引入惯性权重 w［2］.惯性权重 w控制着粒子运动的惯性，使粒子有扩展搜索空间的趋势和开发新区域的能力.惯性权重w的取值对于保证算法的收敛和最优地权衡搜索与开发极其重要，一般地，较大的权重有利于提高算法的全局开发能力，而较小的权重则能增强算法的局部搜索能力.针对惯性权重w的取值问题，国内外的研究人员进行了大量的工作［3-5］，其中线性递减权重法相对简单且收敛速度快，被广泛采用.但是，PSO算法在实际搜索过程中多是高度复杂非线性的，线性递减权重法不能反映实际的优化搜索过程，也有研究人员据此提出了非线性递减法［6-7］和引入其他因素的自适应调整权重法［8］等.本文根据PSO算法惯性权重在优化问题过程中的表现特征，提出了一种基于Logistic模型的动态惯性权重的策略，并与典型的线性递减权重调整策略［3］进行了比较，仿真实验表明:该策略在优化复杂多峰值的问题方面体现了一定的优越性.

1 粒子群优化算法

设第 i个粒子位置为 xi=(xi1，xi2，…，xin)T，其位移为 vi=(vij，vi2，…，vin)T.它迄今搜索到的个体极值为 pi=(pi1，pi2，…，pin)T，而迄今搜索到的种群极值为 pg=(pg1，pg2，…，pgn)T.为使粒子位移变化不致过大，可以设定其上限Vmax，即若 vid＞ Vmax，则令 vid=Vmax，而若 vid＜ -Vmax，也令vid=-Vmax.每一次迭代，粒子通过两个极值pi和pg来更新其速度和位置.粒子在解空间内不断跟踪个体极值和邻域极值进行搜索，直到满足迭代停止条件，即达到规定的迭代次数或满足规定的误差标准.

假设寻优问题为求目标函数f(x)的最小值，那么粒子i的个体极值由下式确定

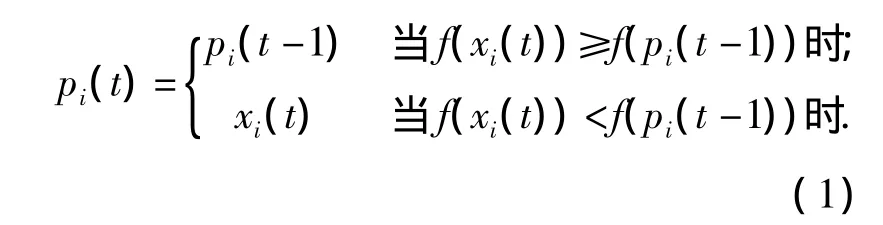
假设群体粒子数为m，则群体粒子的邻域极值为:

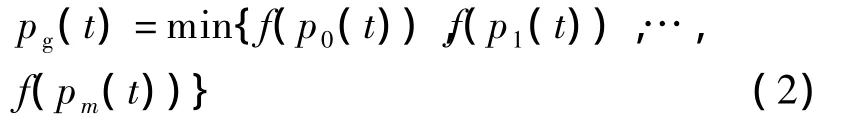
按追随当前已知的最优位置的原理，粒子xi将按式(3)改变位移方向和步长.

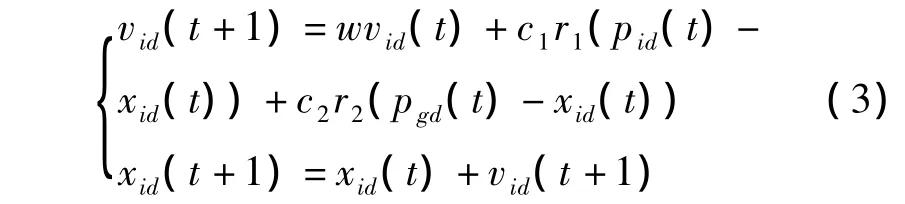
其中:d=1，2，…，n，n 为解空间的维数，即自变量个数，i=1，2，…，m，m 为种群规模，t为进化代数，r1和r2为分布与［0，1］之间的随机数，c1和c2为位移变化的限定因子，通常取为2.0.

w为惯性权重，较大的权重有利于提高算法的全局开发能力，并增加种群的多样性;而较小的权重则能增强算法的局部搜索能力.然而过大的权重将使种群发散，粒子不能改变运动方向以转回需要搜索的指定区域;过小的权重将导致种群的搜索能力丧失，只有很小的惯性从上一步迭代中保存下来，加剧了速度的改变.动态的惯性权重调整通常采用线性递减策略LDIW［9］，即:

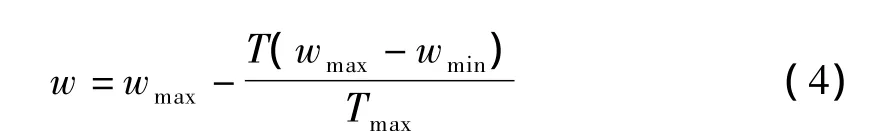
其中T为当前迭代次数，Tmax为最大迭代次数，wmax为初始惯性权值，wmin为进化到最大代数时的惯性权值.

2 非线性权重递减策略

在PSO算法的搜索过程中可以对惯性权重w进行动态调整.在算法开始时，给w选取较大的值，随着搜索的进行，可以动态地递减w的取值，这样可以保证算法在开始时，各粒子能够以较大的速度步长在全局范围内开发较好的种子;而在搜索后期，较小的w值则保证粒子能够在极点周围做精细地搜索，使算法有较大的几率以一定精度收敛于全局最优解.

在标准PSO算法中，存在粒子容易过早收敛于局部极值的早熟现象，在惯性权重线性递减策略中尤为突出.由于仅仅简单地线性减小权重w，使得函数一旦进入局部极值点邻域内就很难跳出，极易收敛到局部极值点.这主要还是因为在搜索过程中，种群中粒子在位置上缺乏多样性导致的早熟.可以考虑在搜索初期尽可能地保持较大的权重w，使种群粒子飞跃整个搜索空间，以获得更好的多样性，从而尽可能摆脱局部极值的干扰;而当种群搜索到全局最优点附近时，及时快速降低权重w，并在搜索后期保持较小的权重w，使得种群以较强的局部搜索能力收敛到全局最优点.据此，根据Logistic函数的特征，提出一种基于Logistic动态调整惯性权重w的策略LgDW算法，惯性权重w将按S形曲线非线性递减，如图1所示.

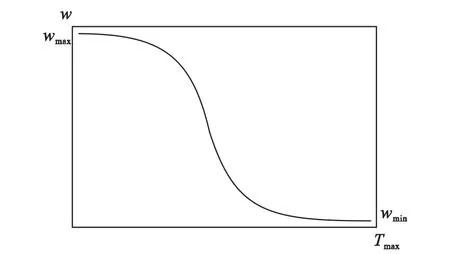
图1 Logistic动态惯性权重w变化趋势Fig.1 The evolution of Logistic dynamic inertia weight

其变化公式为

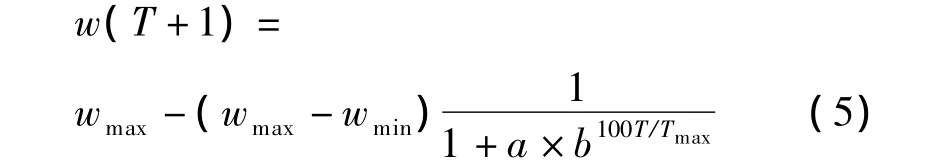
式中:wmax、wmin、Tmax和 T与(4)式一致;a和 b为调整因子，它们的取值范围为a＞0，0＜b＜1.

3 实验分析

为检验Logistic动态惯性权重PSO算法的效率，并分析确定调整因子，现采用优化领域中常用的4个经典函数来测试分析.

Sphere函数:

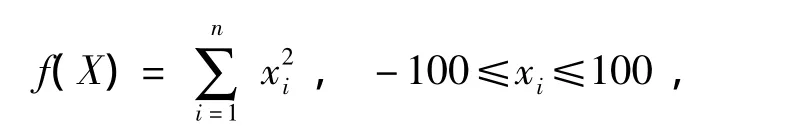
其为非凸、病态函数，在xi=0处达到全局最小值f(X*)=0.

Rastrigrin函数:

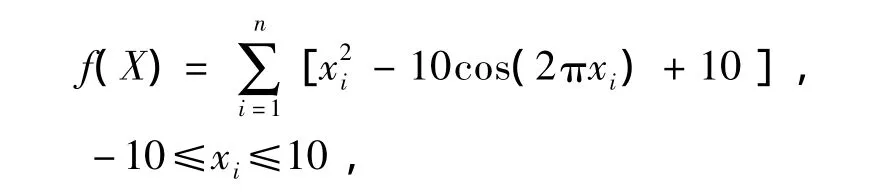
其为多峰函数，在xi=0处达到全局最小值f(X*)=0.

Griewank函数:

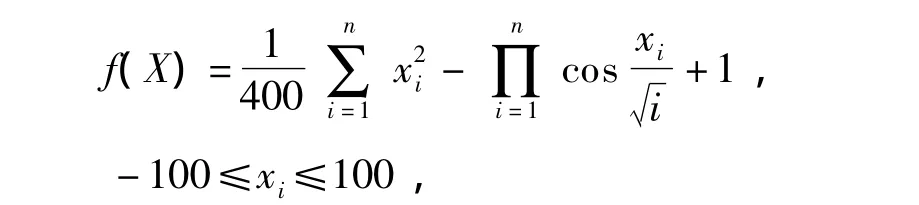
其在xi=0处达到全局最小值f(X*)=0.Schaffer函数:

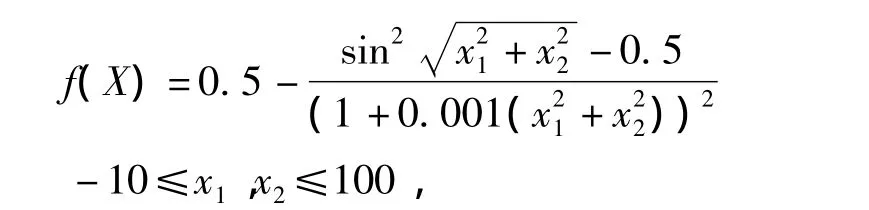
其全局最大值为f(0，0)=1，在距离全局最大点附近存在大量的次全局极大点，函数的强烈震荡使其难于全局最优化.

3.1 调整因子的确定

LgDW算法惯性权重公式(5)中的调整因子a和b可以根据目标函数不同的适应值动态地确定，它们对算法的性能有较大的影响.实验表明:过大的a和b值容易使算法失效，而过小的a和b值则容易使算法陷入局部收敛.它们的取值在10＜a＜50，0.8＜b＜0.93时，算法的性能比较好.表1、表2所示的是在a和b不同取值下对5维Rastrigrin函数的实验结果，实验中算法的每组因子随机运行50次，粒子数为30，要求精度为10-8，最大迭代次数为2 000次.

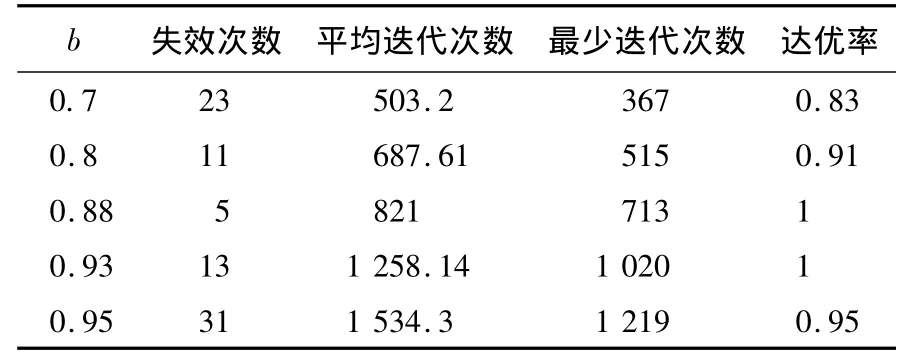
表1 a=30时取不同b值的性能比较Table 1 Comparative results of different b values with a=30

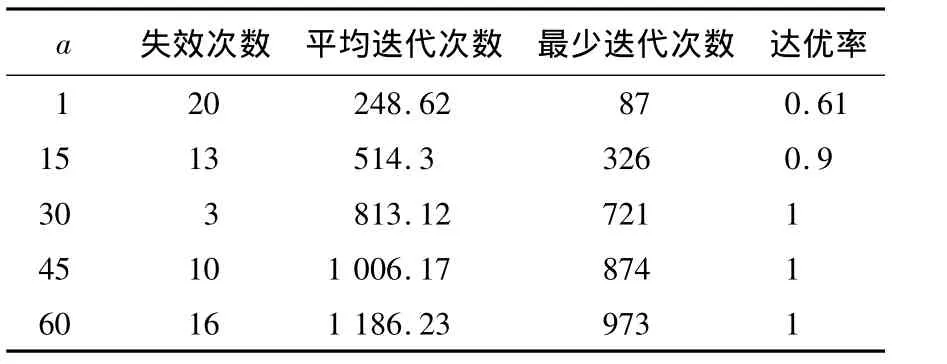
表2 b=0.88时取不同a值的性能比较Table 2 Comparative results of different a values with b=0.88

3.2 数值实验和结果分析

实验中，分别用LDIW策略 PSO算法和LgDW策略PSO算法对4个测试函数进行计算，参数取值 wmax=1.2，wmin=0.1，c1=c2=2.0，a=30，b=0.88，随机运行50次，粒子数为30.实验所得的各测试函数平均最优适应值进化情况如图2～图5所示，数值结果如表3所示.

由进化曲线图可以看出:除了单峰Sphere函数，在优化多峰值的复杂函数(Rastrigrin函数、Griewank函数和Schaffer函数)方面，LgDW策略PSO算法都能较快地收敛于最优解，优于线性递减策略的PSO算法.这主要是较大的惯性权重有利于全局探索，而较小的惯性权重有利于算法的局部开发，加速算法的收敛.

由实验所得的数值结果可以看出:LgDW策略PSO算法对于后面3个多峰函数的优化，最优值、均值及方差均有所改善，其主要原因是在初期较大的惯性权重能增大算法的搜索能力，保持了种群的多样性;而在Sphere函数和高维的Griewank函数改善较小，是因为Sphere函数为单峰函数，而超过15维后Griewank函数特性趋于单峰.说明LgDW策略PSO算法对于多峰值复杂函数具有一定的优越性.

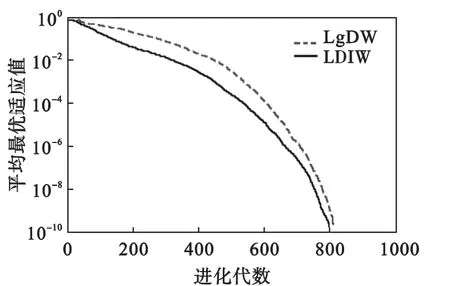
图2 Sphere函数平均最优适应值进化曲线Fig.2 Comparative evolutionary process on Sphere

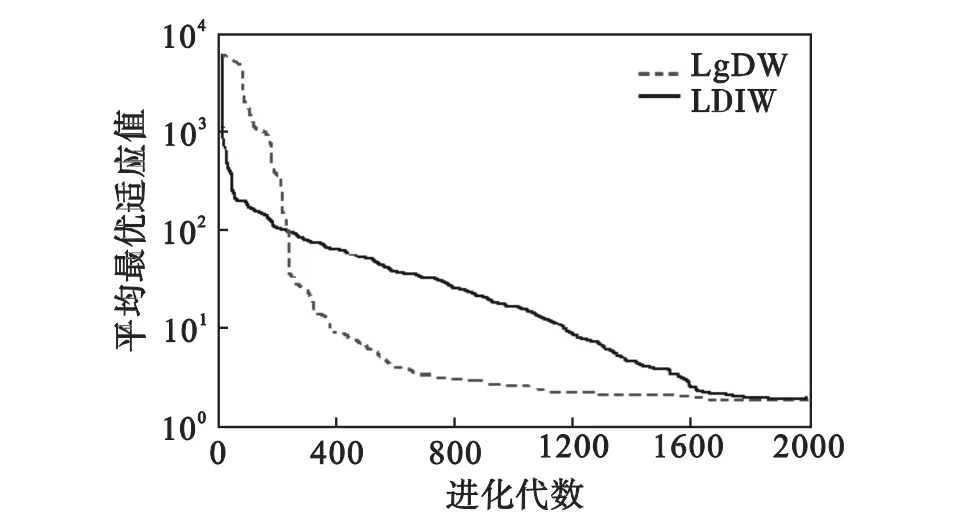
图3 Rastrigrin函数平均最优适应值进化曲线Fig.3 Comparative evolutionary process on Rastrigrin

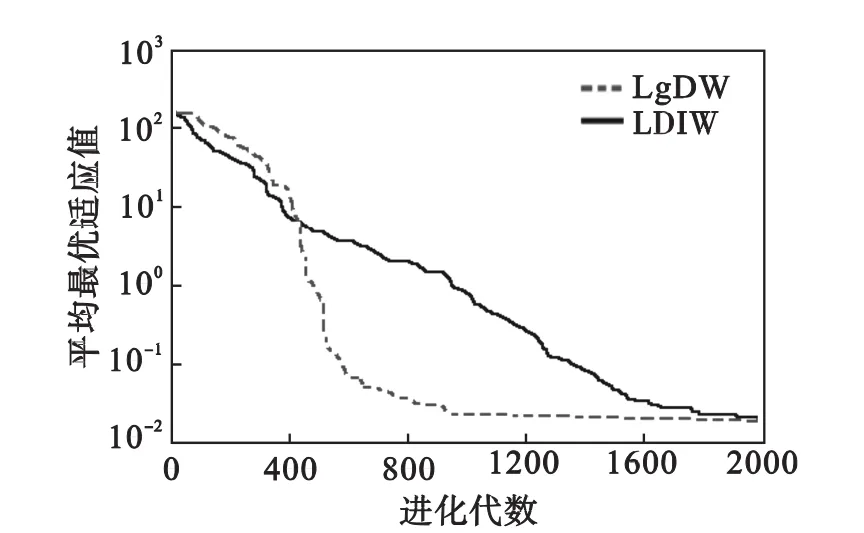
图4 Griewank函数平均最优适应值进化曲线Fig.4 Comparative evolutionary process on Griewank

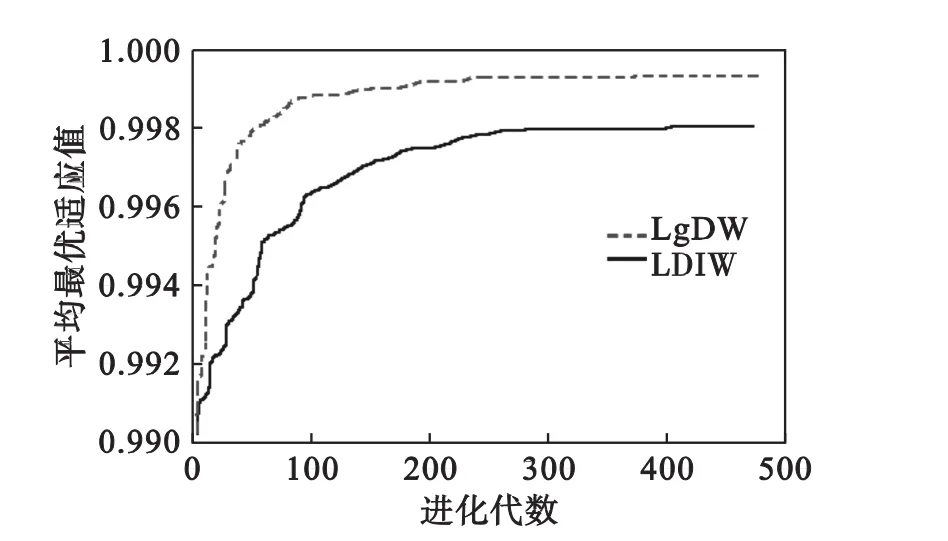
图5 Schaffer函数平均最优适应值进化曲线Fig.5 Comparative evolutionary process on Schaffer

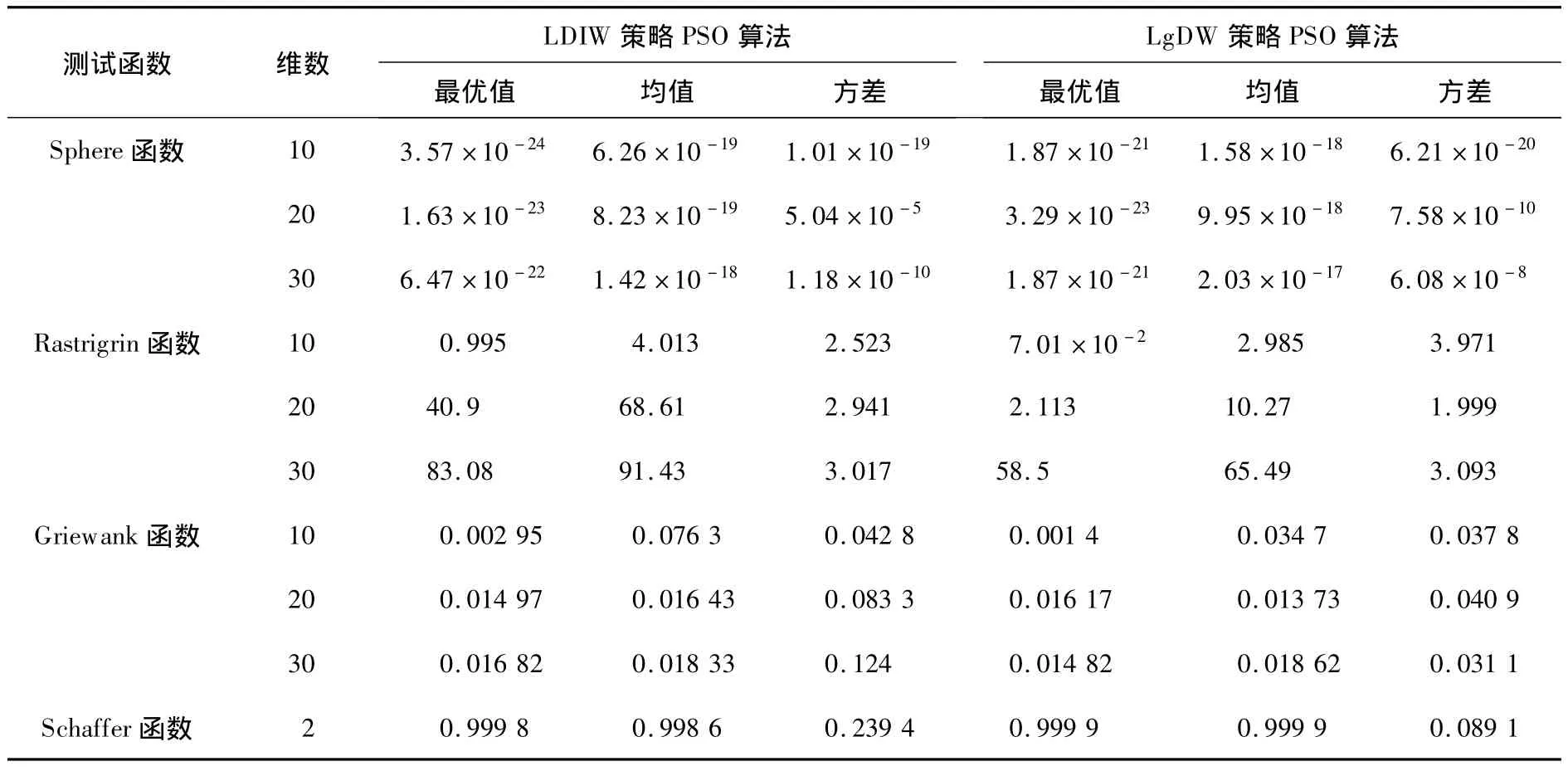
表3 数值结果统计Table 3 Comparative results of LDIW and LgDW on Test Problems

4 结论

作为新的进化计算方法，粒子群优化(PSO)给大量非线性、不可微和多峰值复杂问题的优化提供了一种新的思路.本文根据PSO算法惯性权重在优化问题过程中的表现特征，提出了一种基于Logistic模型的动态惯性权重的LgDW策略，数值实验表明:LgDW策略对于多峰值的复杂函数的优化体现出了较好的性能，具有一定的优越性.

［1］ Kennedy J，Eberhart R C.Particle Swarm Optimization［C］//Proc of IEEE Int Conf on Neural Networks.Perth:IEEE，1995:1942-1948.

［2］ Shi Y，Eberhart R C.A Modified Particle Swarm Optimizer［C］//Proceedings of the IEEE Congress on Evolutionary Computation.Now York:IEEE，1998:303-308.

［3］ Shi Y，Eberhart R C.Parameter Selection in Particle Swarm Optimization［C］//In Proceedings of the Seventh Annual Conference on Evolutionary Programming.New York:Springer-Verlag，1998:591-600.

［4］ Shi Y，Eberhart R C.Fuzzy Adaptive Particle Swarm Optimization［C］//The IEEE Congress on Evolutionary Computation.San Francisco:IEEE，2001:101-106.

［5］ Eberhart R C，Shi Y.Tracking and Optimization Dy-namic Systems with Particle Swarms［C］//The IEEE Congress on Evolutionary Computation.San Francisco:IEEE，2001:94-100.

［6］ Chatterjee A，Siarry P.Nonlinear Inertia Weight Variation for Dynamic Adaptation in Particle Swarm Optimization［J］.Computers and Operations Research，2006，33(3):859-871.

［7］ 陈贵敏，贾建援，韩琪，等.粒子群优化算法的惯性权重递减策略研究［J］.西安交通大学学报，2006，40(1):53-56.

［8］ 张选平，杜玉平，秦国强，等.一种动态改变惯性权的自适应粒子群算法［J］.西安交通大学学报，2005，39(10):1039-1042.

［9］ Shi Y H，Eberhart R C.Empirical Study of Particle Swarm Optimization［C］//Proc of IEEE Congress on Evolutionary Computation.Washington:IEEE，1999:629.