高温多轴载荷下低周疲劳寿命预测
2013-10-30王昭春田大将
金 丹, 王昭春, 田大将, 钟 瑜
(1.天津大学化工学院,天津 300072;2.沈阳化工大学能源与动力工程学院,辽宁沈阳 110142;3.盘锦辽河油田锦州采油厂作业一大队,辽宁锦州 121209)
随着现代工业的迅速发展,生产规模的大型化、复杂化和高参数等造成了结构件发生疲劳失效的事故逐年增加,构件的疲劳失效问题引起了极大重视.为提高热效率以及更好地保护环境,当前,欧美各主要发达国家都在研究开发高蒸汽参数和高效率化的超临界机组.随着新建机组的使用,对钢材的高温性能提出了更高的要求,Mod.9Cr-1Mo钢因其优异的高温持久性能、良好的导热性、较低的生产成本,成为火力发电厂动力设备的主要耐高温材料或更新换代材料,目前该钢种在我国电厂中得到了日益广泛的应用[1].当前从工艺条件、焊接分析等方面针对该材料进行了一些研究[2],同时也有一些关于该材料本构关系等的研究,例如 Yaguchi针对Mod9Cr-1Mo钢进行了一系列不同温度的循环变形试验,包括不等温试验,将粘塑性本构模型拓展到用于Mod9Cr-1Mo钢不同温度下的循环变形分析[3].但针对其高温多轴疲劳研究工作较少.近些年来,对低周疲劳寿命预测的研究取得了很大的进展,提出了许多比较有效的疲劳预测模型.目前对常幅载荷下多轴低周疲劳破坏的寿命预测主要有3种方法:等效应变法、能量法和临界面法[4].针对大部分材料,等效应变方法能够较好地预测单轴和比例加载下材料的疲劳寿命.
由于Mod.9Cr-1Mo耐热钢的实际使用条件通常在600℃以下,因此,本文针对该材料进行550℃下的低周疲劳试验,定义主应变比φ来比较不同比例程度对疲劳特性的影响.针对5个主应变比进行高温多轴疲劳试验,采用最大正应变方法、最大剪应变方法和von Mises等效应变法进行疲劳寿命预测,对3种方法的预测结果进行比较分析.
1 试验
所用材料为Mod.9Cr-1Mo铁素体钢,550℃下材料的屈服应力σy=348 MPa,弹性模量E=170 GPa,泊松比μ=0.3.采用薄壁管进行试验,具体尺寸如图1所示.
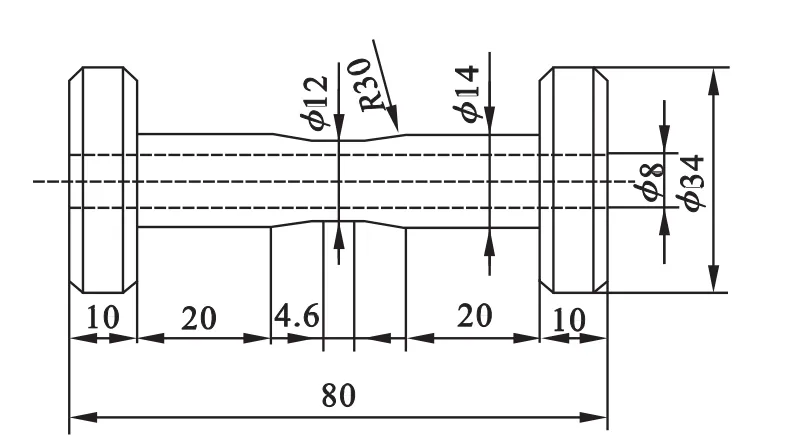
图1 试件形状及尺寸Fig.1 Shape and dimensions of the specimen
试验在多轴液压疲劳试验机上进行,高周波诱导加热,试验中控制标距段温差±5℃,von Mises等效应变速率0.1%/s,完全对称三角波控制,von Mises等效应力水平下降至稳定应力水平下5%即为失效.所进行的试验均为比例加载的多轴试验,主应变比定义为 φ =ε3/ε1,ε3为第三主应变,ε1为第一主应变,φ=-0.5对应单轴情况,φ=-1.0对应于纯扭转情况,其他主应变比分别为φ=-0.54,-0.64,-0.8.试验结果见表1.试验中得到一个循环内正应变及剪应变值,依据材料力学中相应公式,采用Matlab软件进行各个面上正应变及剪应变的计算,在0°~180°面内,每隔1°进行应变值计算.
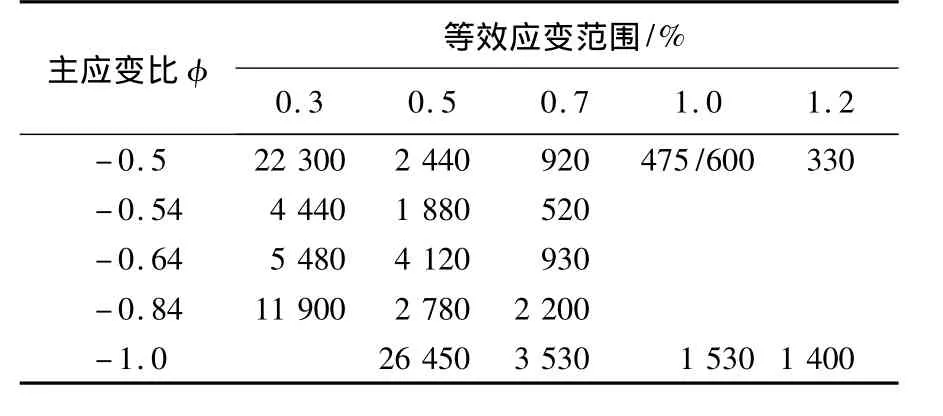
表1 试验结果Table 1 Test results
2 高温循环软化特性分析
图2给出不同应变幅值、应变路径下von Mises等效应力随循环数的变化关系.从图2可以看出:材料在最初几个循环内略表现出应力增加的趋势,随即达到应力最大值.在所有路径下,材料均表现出循环软化的特性,这与文献[5]的结果一致.在单轴路径下,即φ=-0.5,循环软化特性随应变幅值的增加而愈加明显,其值分别为,当Δεeq=0.3%,应力降低量为16.3%,当Δεeq=1.2%时,应力降低量为22.8%,平均值为20.7%.但在其他路径下,其软化趋势随着应变幅值的增加并不明显.当φ=-0.54时,其平均软化程度为22.9%;当φ=-0.64时,其平均软化程度为26.5%;当φ=-0.84时,其平均软化程度为34.5%;当φ=-1.0时,其平均软化程度为35.3%.总之,路径对循环软化特性的影响大于应变幅值对循环软化特性的影响,其软化程度随扭转载荷所占比例增加而增加.
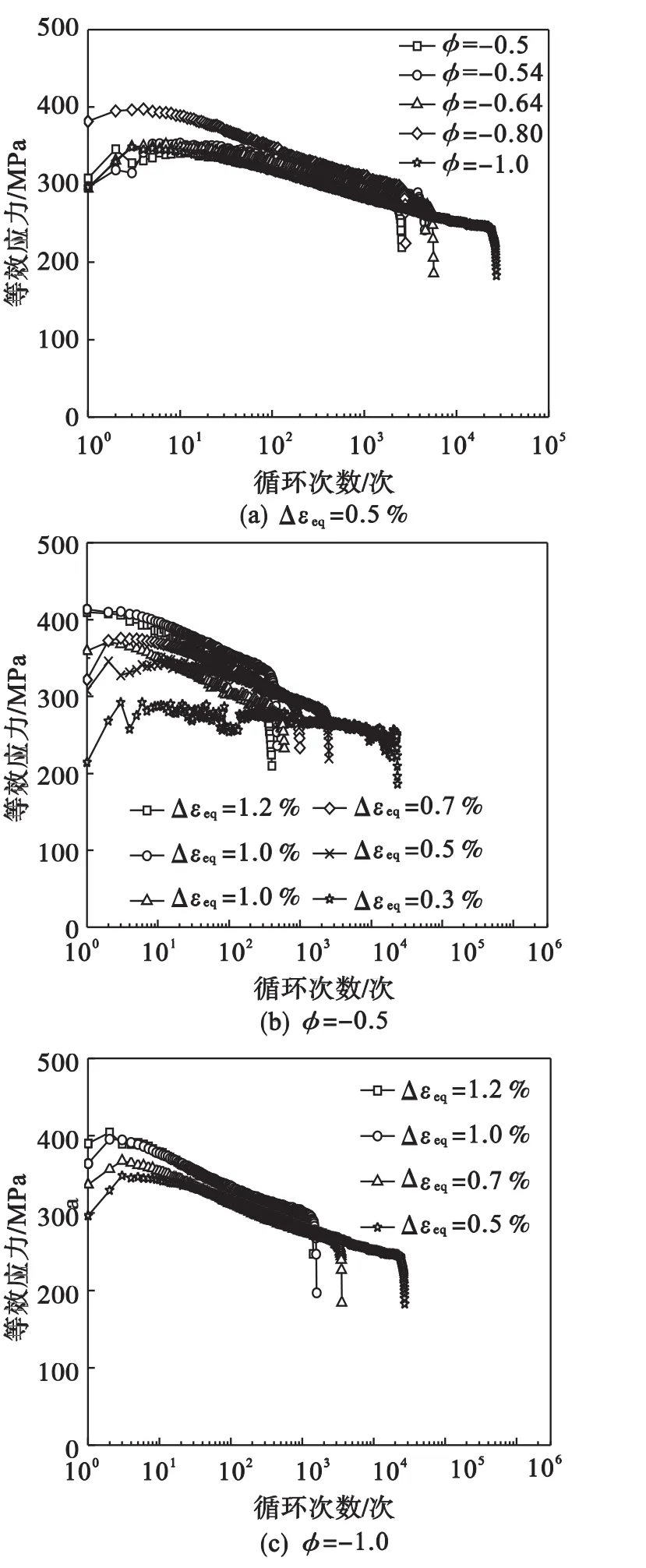
图2 等效应力与循环次数关系Fig.2 Equivalent stress amplitude vs number of cycles
3 疲劳寿命预测
3.1 疲劳寿命预测模型
近些年来,对多轴低周疲劳损伤累积和寿命估算方法的研究取得了很大的进展,提出了许多比较有效的疲劳预测模型.Manson等人[6-8]提出了等效应变理论,这些等效应变包括:最大剪应变、最大法向应变、von Mises等效应变、八面体剪应变等.这种从静强度理论引用过来的方法称为等效应变法.一些研究表明,不同的等效应变方法差异并不大,对于比例加载情况,简单有效.本文采用最大正应变方法、最大剪应变方法和von Mises等效应变方法进行寿命预测,各模型如下:
(1)最大正应变方法
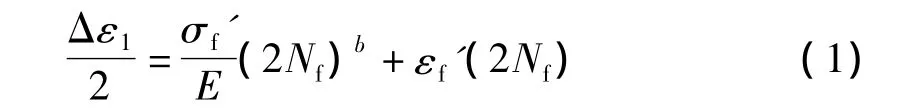
(2)最大剪应变方法
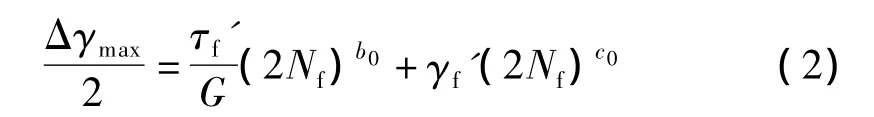
(3)von Mises等效应变方法
利用Mises等效应变幅作为多轴疲劳损伤参量,其寿命预测表达式如下:
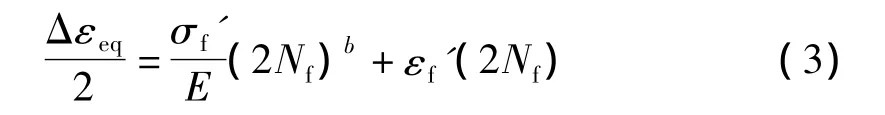
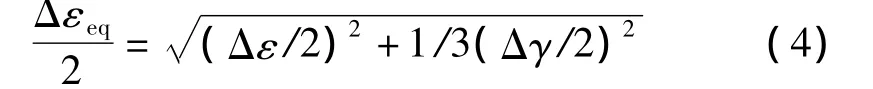

表2 材料疲劳性能常数Table 2 Fatigue property constant
3.2 疲劳寿命预测结果讨论
应变法是最初用于疲劳寿命预测的方法,针对大部分比例载荷的情况简单有效.上述3种疲劳寿命预测方法得到的预测结果如图3所示.
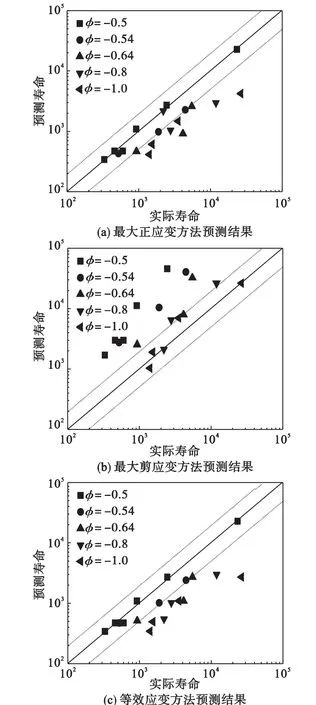
图3 疲劳寿命预测结果Fig.3 Fatigue life prediction results
最大正应变方法在预测扭转载荷时,得到的预测结果偏于保守,对其他路径的预测随着扭转载荷的增大,预测结果偏于安全.而最大剪应变方法预测扭转载荷较好,但对于其他路径,尤其是针对单轴路径,给出的预测结果过于不安全.等效应变法对多种材料比例载荷下的寿命预测都给出了比较满意的结果,但对本文所用材料,该方法得到的结果偏于保守.3种方法从本质上相差不多,但对于该材料,550℃下各路径及各应变幅值下均表现出了明显循环软化现象,相同等效应变幅值下扭转载荷的寿命为拉压载荷下的3倍,小应变幅值下高达10倍.因此,造成等效应变法得到的结果随着φ值的降低预测值偏低.从预测结果对比可知:最大正应变方法预测结果好于其他两种方法,大部分结果位于2倍分散带内.
4 结论
基于试验结果,针对材料循环软化特性的路径及幅值相关性进行分析,采用应变方法进行疲劳寿命预测,得到如下结论:
(1)针对Mod.9Cr-1Mo钢进行550℃下单轴、扭转和比例载荷下的低周疲劳试验,定义主应变比φ用以考虑不同的比例程度对多轴疲劳寿命的影响.
(2)试验结果表明:各路径下材料均表现出明显的循环软化现象,但路径对循环软化特性的影响大于应变幅值对循环软化特性的影响,其软化程度随扭转载荷所占比例增加而增加,即单轴载荷下,平均软化程度为20.7%,而在扭转载荷作用下平均软化程度为35.3%.
(3)采用最大正应变方法、最大剪应变方法和von Mises等效应变法进行疲劳寿命预测.预测结果表明:最大正应变方法针对单轴路径给出了较好的预测结果,但针对扭转路径下预测结果偏低.而最大剪应变方法针对扭转路径预测结果较好,但针对单轴路径预测结果偏于不安全.等效应变法的预测结果偏于保守.总之,最大正应变方法预测结果好于其他两种方法,大部分结果位于2倍分散带内.
[1] 王卫泽,王钥,朱月梅,等.我国P91/T91钢生产及其性能的现状与进展[J].机械工程材料,2010,34(4):6-9.
[2] ARIVAZHAGAN B,SUNDARESAN S,KAMARAJ M.A Study on Influence of Shielding Gas Composition on Toughness of Flux-cored Arc Weld of Modified 9Cr-1Mo(P91)Steel[J].Journal of Materials Processing Technology,2009,209:5245-5253.
[3] YAGUCHI M,TAKAHASHI Y.A Viscoplastic Constitutive Model Incorporating Dynamic Strain Aging Effect during Cyclic Deformation Conditions[J].International Journal of Plasticity,2000,16:241-262.
[4] 金丹,陈旭.多轴随机载荷下的疲劳寿命估算方法[J].力学进展,2006,36(1):65-74.
[5] YAMAMOTO M,MIURA N,OGATA T.Applicability of C Parameter in Assessing Type IV Creep Cracking in Mod.9Cr-1Mo Steel Welded Joint[J].Engineering Fracture Mechanics,2010,77:3022-3034.
[6] SMITH R W,HIRSCHBERG M H,MANSON S S.Fatigue Behavior of Materials under Strain Cycling in Low and Intermediate Life Range,NASA TN D-1574[R].National Aeronautics and Space Administration,1963:58.
[7] MORROW J.Cyclic Plastic Strain Energy and Fatigue of Metals.Internal Friction Damping and Cyclic Plasticity[C]//ASTM STP378,Internal Friction,Damping,and Cyclic Plasticity.Philadelphia:American Society for Testing and Materials,1965:45-87.
[8] Fash J W,Socie D F,Mcdodwell D L.Fatigue Life Estimates for a Simple Notched Component under Biaxial Loading,Multiaxial Fatigue[C]//Miller k J,Brown M W.ASME STP853,Multiaxial Fatigue.Philadelphia:American Society for Testing and Materials,1985:497-513.
