沿海城市多水源多用户供水优化配置研究*

高 波 郭菊娥薛欣喜

(1.西安交通大学 管理学院，陕西 西安 710049, 2.青岛海润自来水集团有限公司，山东 青岛 266100)

沿海城市多水源多用户供水优化配置研究*

高 波1郭菊娥1薛欣喜2

(1.西安交通大学 管理学院，陕西 西安 710049, 2.青岛海润自来水集团有限公司，山东 青岛 266100)

针对多水源、多行业用户的城市供水特点，从经济效益、社会效益等角度构建水资源优化配置模型，并以某沿海城市为例分别从各类水资源工程成本、全成本角度对城市供水结构进行了优化及对比，以期在充分利用水资源、保证需水要求的前提下，寻求水资源开发最佳组合模型，实现供水效益的最大化。为全国同类城市水资源利用结构优化起到一定的借鉴作用。

水资源；优化配置；全成本

我国北方沿海城市大多存在严重缺水的实际情况,随着城市建设与经济发展迅速，水资源的供需矛盾问题日益显著，水资源短缺已成为制约当地长远发展的关键问题。在开发新水源的同时，有效利用现有水资源，合理调配多种水源在各类用水户的有机分配，解决供需的分配矛盾、提高用水效益，成为缺水城市解决用水问题的有效途径。

一、水资源优化配置的理论依据

水资源的优化配置可理解为：在一定范围内，遵循有效、公平和可持续性等原则，借助各种有效措施，考虑价值规律，通过合理抑制需求、有效增加供水、积极保护生态环境等手段和措施，对多种水源在时间和空间(包括区域间和各用水部门间)上进行的合理调配。

水资源配置的实施措施包括：通过跨地区、跨流域调水来调剂水资源的余缺；通过水库等调节工程来解决年内和年际水资源分布不均匀的问题；对地表水、地下水、中水回用、外调水、海水淡化等水源进行统一调配，来满足不同用户不同时期的用水需求，保证区域供水要求，促进区域经济的持续稳定发展。

由于水资源的短缺性、分布不均衡性、不可替代性，以及日益激烈的用水竞争性等特点，水资源优化配置研究在解决我国城市水资源短缺问题、实现可持续利用等方面有着极为重要的现实意义。

国外水资源优化配置研究最初源于20世纪40年代Masse提出的水库优化调度问题。后来Nebulas和W.A.Hall首次将动态规划引入地表水和地下水的联合运用和分配。随着系统工程的原理和方法的引入，国外开始用系统分析方法研究水资源问题，许多水资源规划的目标，都由以前的单一强调经济发展，逐步过渡到更广泛的社会需求方面，即多目标规划。

1997年，Wong和Hugh S等提出地表水、地下水、外调水等多水源联合运用的多目标多阶段优化管理的原理和方法。[1]同年Carlos Percia和Gideon Oron则以以色列南部地区为实例构建了以经济效益最大化为目标的多水源供水模型。[2]美国、以色列、日本等国家很早就认识到城市水资源“高质高用、低质低用”的重要性，将污水回用也纳入水资源范畴，将污水回用水用于农业灌溉、工业冷却、景观用水等。[3]A.Burcu Altan Sakarya等建立了污水、地表水和地下水等多种水源的管理模型。[4]Lnjayant C和Chiek U于2003年建立了流域地表水和地下水利用的空间分配模型。[5]

我国水资源配置方面的研究虽然起步较晚，但由于我国特殊的地理环境及水资源保护不力，水资源紧缺的日益突出，使得我国学者在20世纪90年底后期对水资源优化配置方面的研究发展迅速。吴险峰等通过构建多约束的线性规划模型，通过费用效益系数等进行修正求解，对枣庄市水资源进行了供水优化配置。[6]吴英杰等构建锡林浩特市多水源工业供水优化配置模型，并应用NSGA-Π算法进行了求解，但城市水资源优化配置涉及工业、农业、居民生活、公共服务等多个方面，该模型仅考虑工业用水，不能涵盖城市整体水资源的优化配置。[7]岳春芳以珠海市为例，探讨了在复杂水源下的供水优化配置，建立了原水—纯净水耦合配置模型，采用遗传算法进行了解证。[8]谷红梅、孙文等利用动态规划模型构建了城市供水水源优化调度模型。[9-10]叶健等构建了不确定性模糊多目标模型来进行水资源的优化配置。[11]张鑫等利用多目标遗传算法以经济效益、社会效益和环境效益为目标函数，对西宁市水资源进行了优化配置。[12]

综上所述，目前对于水资源的优化配置方面的探讨与研究取得了许多有价值的成果，但大多研究是依据各种水资源的工程成本来进行测算的。但由于水资源全成本的研究及优化配置理论涉及情况十分复杂，至今仍没有形成水资源全成本优化配置的统一公认的理论体系与成熟完善的计算方法。本文将进一步探索基于全成本定价的水资源优化配置理论。

二、我国城市水资源现状及规划分析

我国淡水资源人均占有量仅为世界平均值的l/4，位居世界第109位，已经被联合国列为全球13个人均水资源最贫乏的国家之一。在全国661个城市中有420个以上的城市缺水，缺水量约70亿m3。而且我国水资源与经济发展格局极不匹配。长江以北的广大地区人口占全国的47%，耕地占全国的65%，水资源却仅占全国的19%，沿海地区的水资源严重不足，特别是长江以北的沿海城市更为严重，大部分城市和地区人均水资源量低于500m3的国际缺水标准，2010年全国34个主要沿海城市供水状况统计，人均用水低于100m3/a的城市有26个，占城市统计总量的76.4%。北方部分流域水资源的开发程度已经接近甚至超过其利用极限，部分北方沿海城市已面临严重的缺水问题。淡水资源危机，已成为制约我国沿海城市和地区经济和社会发展的重要因素。在此背景下，20世纪80年代末期我国北方城市先后启动了外调水量工程，如黄河流域各城市的引黄补济工程，近年来向流域城市补水耗用的河川径流量为370亿m3；近年来实施的南水北调工程，计划每年将长江流域的200亿m3水量通过东、中、西三线向我国北方区域补充供水。同时，有条件的十余沿海城市(如天津、青岛等)纷纷通过海水淡化来补充城市供水。“调水”应与“节水”并重，各城市在加大供水能力的同时，也纷纷通过水源优化配置等节水措施来保障供需匹配。

以华北沿海城市青岛为例，该市年平均水资源总量为23.9亿m3，人均占有水资源量334m3，亩均耕地占有量330m3，分别为全国平均值的13%和18%，本地淡水资源极其贫乏，可进一步开发的水资源量十分有限，淡水资源不足已经制约着当地经济和社会的发展，外调区域外淡水及发展海水淡化成为该市解决水量短缺的途径，水资源优化配置也成为重要节水手段。

青岛市水资源现状为：城区所辖七区包括：市南区、市北区、四方区、李沧区、黄岛区、城阳区和崂山区。区域水资源时空分布不均，水源地分布也极不均匀，目前供水水源主要有：地表水、地下水、引黄济青水、海水淡化水、中水回用水五大类，未来还会有南水北调水。目前，该市七区城市供水水源综合生产能力为125.82万m3/d。

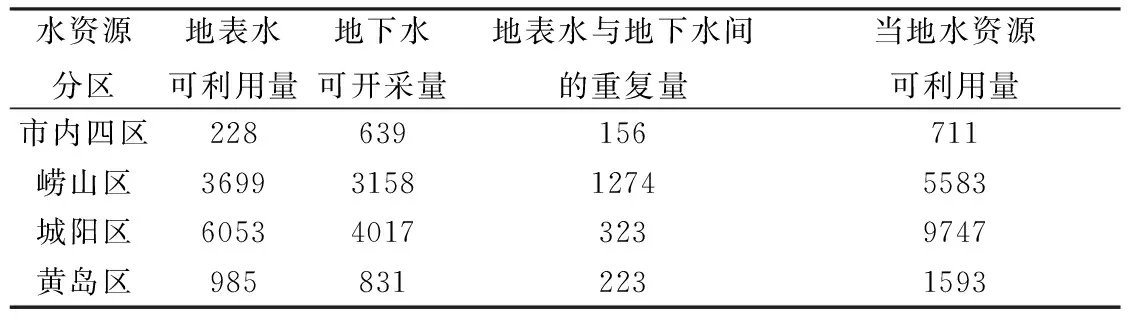
表1 2010年青岛市城区水资源可利用量表(万m3)

注：其中部分郊区的地表供水水源如产芝水库、尹府水库、吉利河水库等水源向城区供水。

根据《青岛市海水淡化产业发展规划》，2010年海水淡化能力达到20万m3/d(年供水量增加0.73亿m3)。规划到2020年日供能力达40万m3/d。2015年为26.4万m3/d。

中水回用仅可用做市政杂用水、生活杂用水、农业用水和景观用水等；《青岛市中水利用规划》中提出到2010年再生水利用量21.7万m3/d，规划到2020年，污水再生利用量达到60万m3/d。

2010年城区各行业部门用水情况如表2所示：

表2 2010年青岛市城市供水综合表

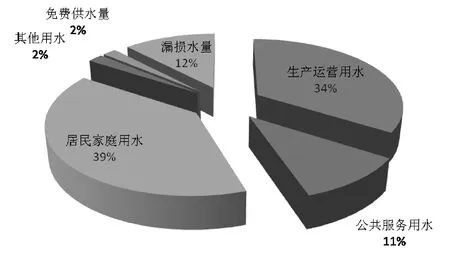
图1 2010年青岛市城市供水类别百分比

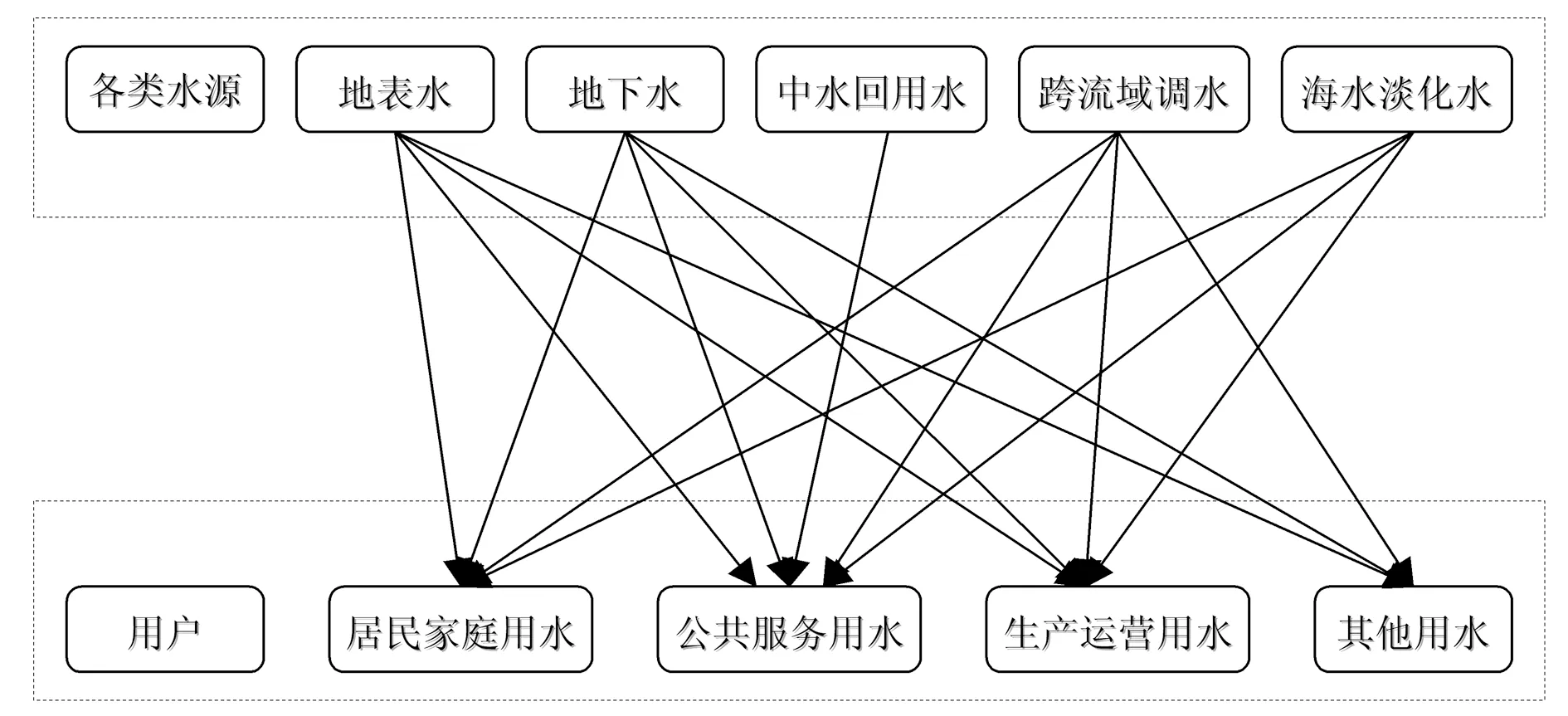
图2 青岛市多水源多用户供水系统图

根据《青岛市城市供水规划(2008-2020)》可以得知到2015年该市供需水量具体见表3、表4：

表3 2015年青岛市需水量预测表(万m3)

表4 2015年青岛市供水量预测表(万m3)

注：其中跨流域调水量主要为外调水的库容量，远期将补充部分外调水量。

三、水资源优化配置实证分析

对于多水源多目标的优化配置研究的数学模型主要有线性、非线性和动态规划模型，国内多水源优化配置研究主要选择线性模型。供水结构优化配置是多水源、多目标的资源分配问题，因多水源联合供水问题上存在于许多的不确定性，需要综合考虑各方面的因素，因此我们以线性规划模型为基础，将动态规划引入水资源优化配置中，以带约束条件的经济效益最大化目标来进行研究。

本文所建模型设定供水方式有i(i=1,2,3,4,5)种：地表水、地下水、跨流域调水、中水回用水、海水淡化水五种。其用户则有j(j=1,2,3,4)个：居民家庭用水、生产运营用水、公共服务用水、其他用水等。其水资源系统可以概括为五种水源、四种用户的优化配置关系。各水源每年的供水量为Qi，水资源价格为pi，用户j实际用水量为Qj，xij为i水源供给j用户的供水量。

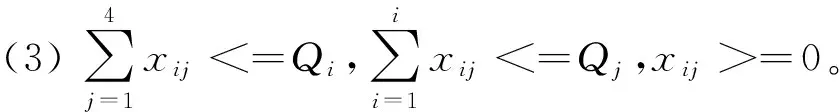
供水效益计算方法主要有最优等效替代工程费用法、影子价格法、缺水损失法和分摊系数法等，其中分摊系数法能够综合反映效益与费用的关系，结合城市供水实际，数据的获得较为容易，本文采用分摊系数法来确定各种用水的效益系数。

(一)效益系数aij

1、生产运营用水主要指的是工业和商业用水，其效益系数可采用工业总产值分摊方法，[13]计算公式如下：

aij=β·(1/w)

式中，β指工业用水效益分摊系数，不同的取水水源，其分摊系数不同，以城市供水管网直接取用自来水的，其分摊系数取5%，以水库、外引水等水利工程为取水水源的取8%；w指工业万元产值取水量(m3/万元)。

假设某市2010年人均生产总值3.64万元,人均占有水资源量313m3，工业万元产值取水量为116.29m3/万元。以城市供水管网直接取用自来水的，其效益系数为5.81，以水库、跨流域调水等水利工程为取水水源的效益系数为9.3。

2、居民家庭用水的效益系数计算如下：[14]

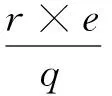
式中，αi1为居民家庭用水效益系数；r为居民可支配收入；e为恩格尔系数；q为该市人均年用水量；η为生活用水效益分摊系数。

假设某市2010年居民可支配收入为24998元，恩格尔系数为38.5%，生活用水效益分摊系数取为0.3。[15]

则该市居民家庭用水的效益系数为9.2。

3、公共服务用水和其他用水的效益系数(其效益是间接而复杂的，不仅有经济方面的因素，而且有社会效益存在，因而其效益系数比较难确定。根据中水回用优先用于公共服务用水的原则，本文在计算中赋予较大的权值，用以表示其效益系数的计算公式为：

αi4=bi4-b34，(i=1,2,4)

式中，αi4为公共服务用水效益系数；bi4为i水源用于公共服务用水的费用系数；另外我们赋予α34=b34。

4、其他用水则赋予较小的权值，用以表示其效益系数，取生产运营用水效益系数的0.875。[16]

(二)费用系数bij

这里我们分为两类讨论：一类是不考虑其外部成本情况下，以各水源供水成本来作为其费用系数；另一类是考虑外部成本情况下，以各水源其供水全成本来作为其费用系数。

假设某市各水源供水成本为：地下水3.6元/m3，地表水4.2元/m3，跨流域调水为5.05元/m3，海水淡化为5.485元/m3，中水回用为1.79元/m3。

全成本(考虑资源成本、外部成本)情况下该市各水源供水全成本为：地下水6.693元/m3，地表水5.494元/m3，跨流域调水为5.654元/m3，海水淡化为7.116元/m3，中水回用为1.98元/m3。[17]

优化计算：

(1)不考虑各水源外部成本情况

通过对表5分析我们可以得出，应首先利用地下水供给居民家庭用水，用地表水供给生产运营用水，如果地下水不能满足居民家庭用水，可以用地表水进行补给，如果地表水不能满足生产运营用水，则用地下水来补充。如果地表水和地下水供给量满足不了居民家庭和生产运营用水，其缺水量由跨流域调水补充，其次考虑用海水淡化水来供给，而中水回用只能用于公共服务用水，具体结果见表6。

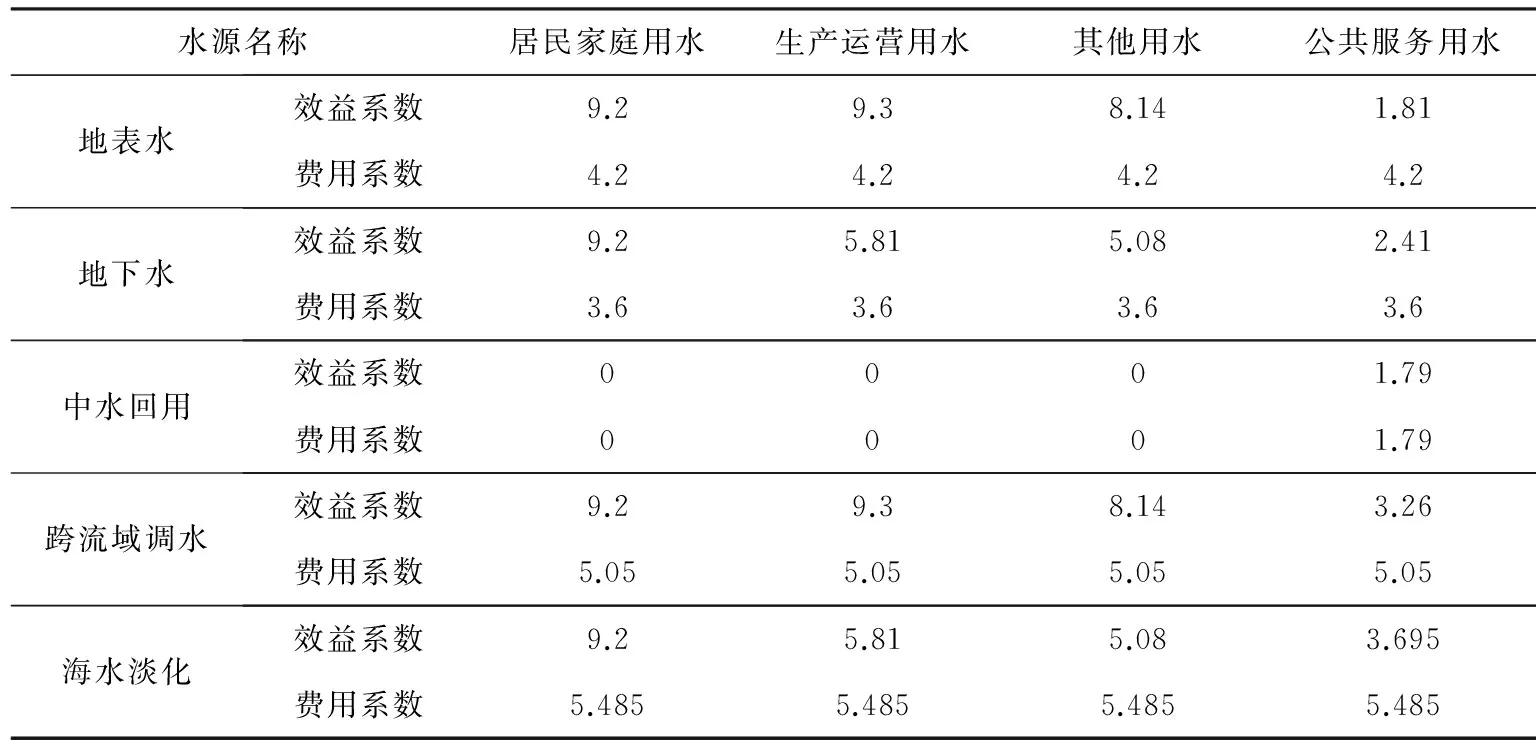
表5 不同水源不同用户供水效益费用系数表(元/m3)

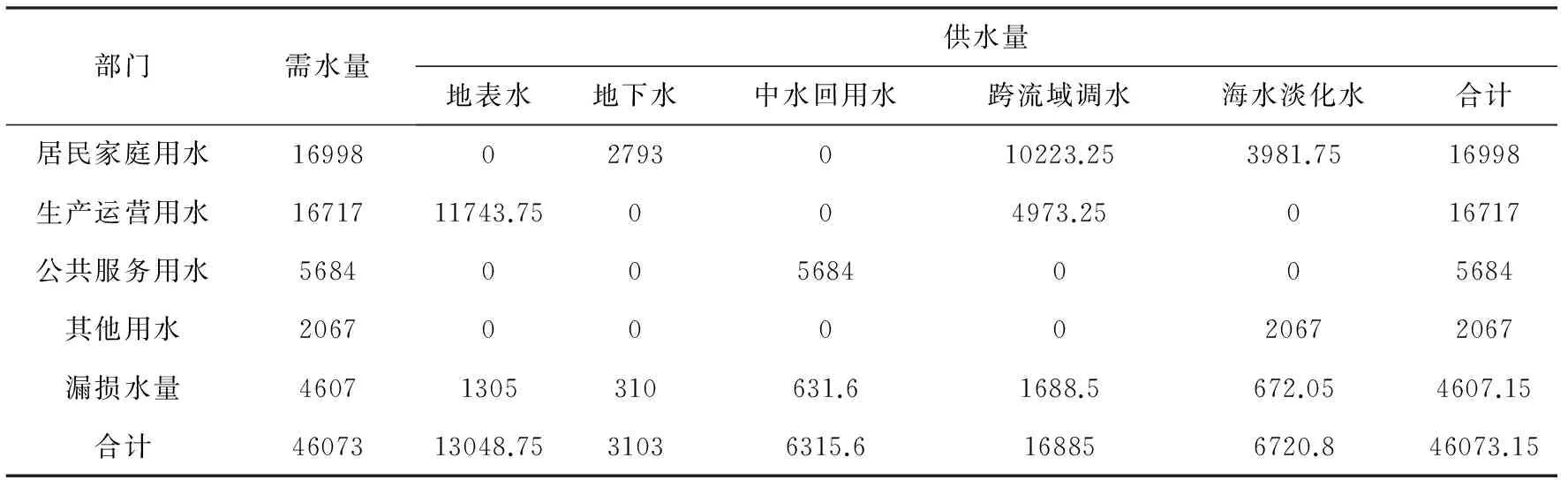
表6 2015年水源优化配置成果表(万m3)

由表6可知供水量合计为46073.05，可以满足该市的需水要求，从表6中也可以看出，地下水应首先用来满足居民家庭用水，而地表水主要用来满足生产运营用水，跨流域调水在满足生产运营用水的基础上为居民家庭提供用水，海水淡化作为备用来弥补居民家庭用水供水量的不足，公共服务用水完全可以采用中水回用水进行供给。

(2)考虑各水源全成本情况

在考虑全成本情况下(见表7)，应首先考虑用地表水来供给生产运营用水，在此基础上居民家庭用水由剩余地表水和地下水进行供给，其次跨流域调水优先供给生产运营用水，如果居民家庭用水仍未能满足，由于中水回用不能用于居民家庭用水，这里需要用跨流域调水进行补充，如果跨流域调水剩余水量仍不能满足居民家庭用水量，再考虑用海水淡化补充居民家庭用水和其他用水，中水回用水用于公共服务用水，具体结果见表8。

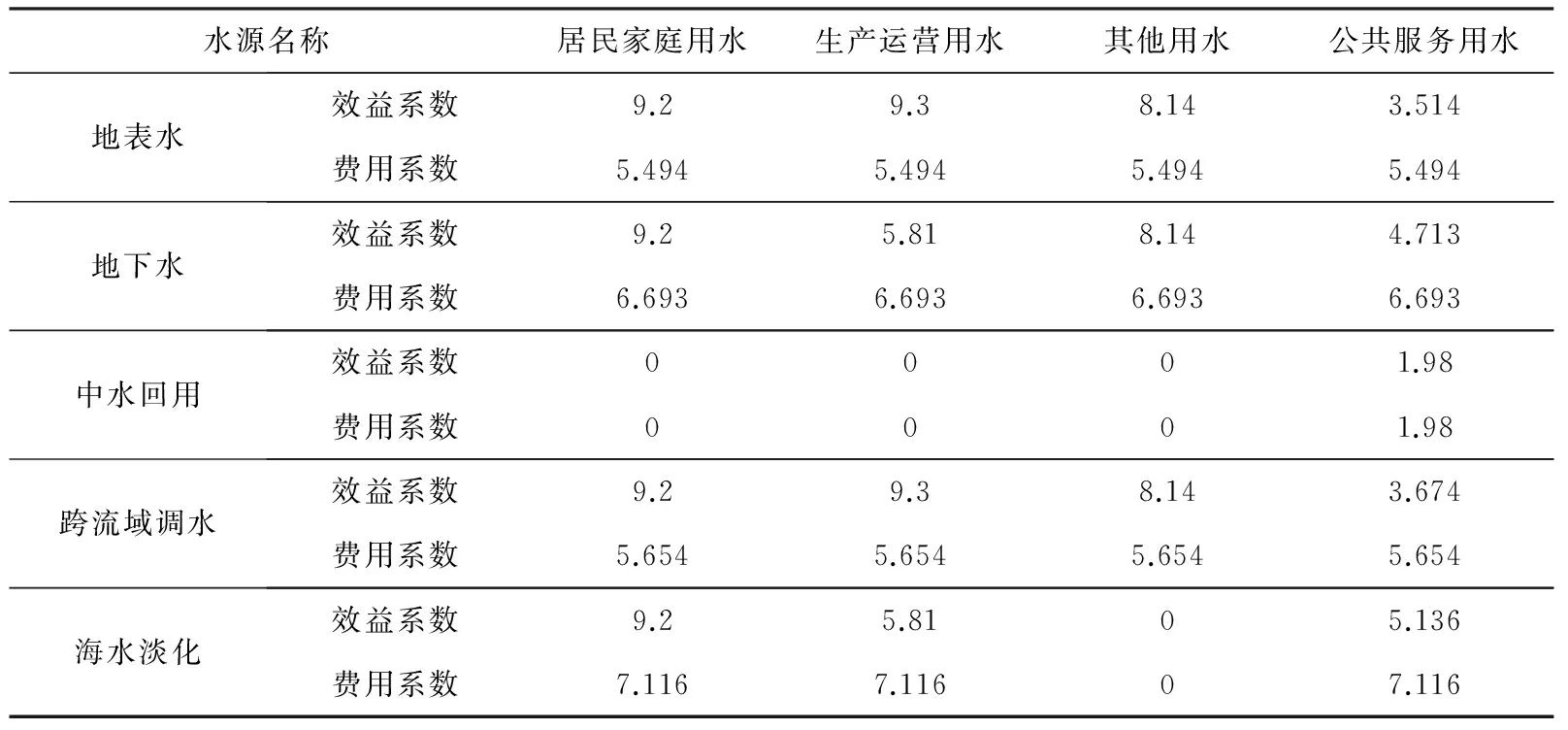
表7 不同水源不同用户供水效益费用系数表(元/m3)

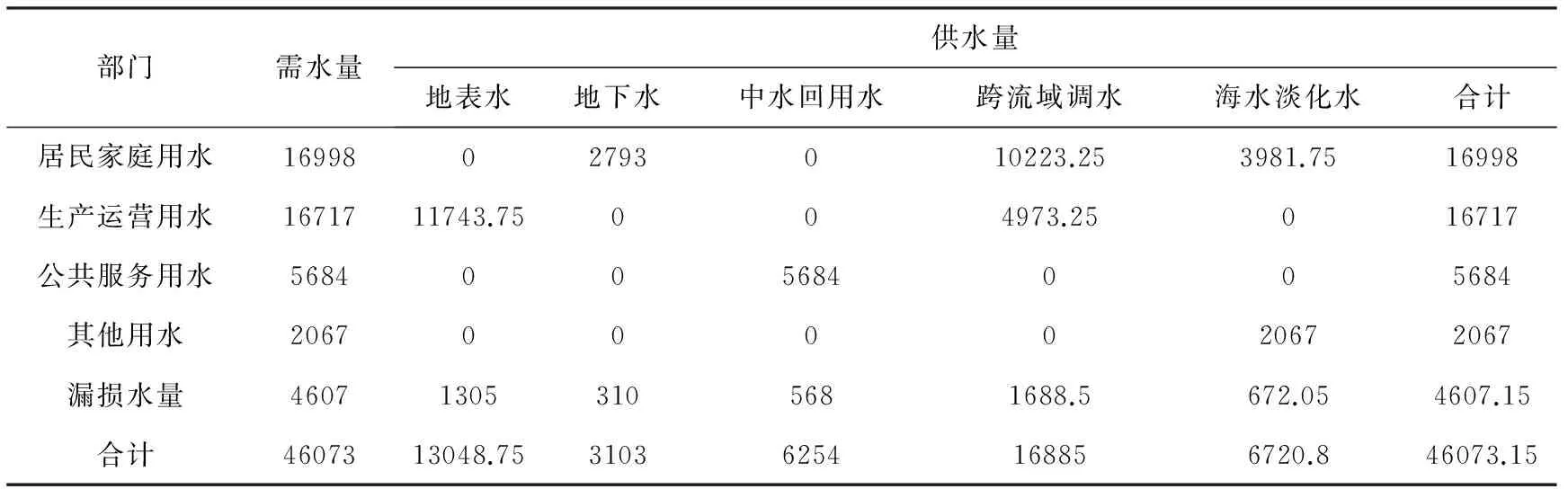
表8 2015年水源优化配置成果表(万m3)

以上分析可得，在采用两种不同的费用系数的前提下，虽然水资源优化配置表6与表8结果相同，但是优化配置的验算过程是不一样的。如其他实例可能会出现供给模式不同的情况。

通过水资源优化配置研究，可得知：水量不足情况下，应依据各类用户的社会及经济重要性来顺次保障供水；水量充足情况下根据水源的成本及效益系数实施优化配置供水，实现经济及社会效益最优；特定水质水源(如中水)只能满足特定需求(如公共服务用水)，应创造条件提高其利用率，以节约优质水量；应从全成本角度考虑水量优化配置，以实现社会及经济效益最优。上述原则，是各城市实施水资源优化配置的决策参考依据。

四、结语

探讨城市多水源多用户情况下的供水优化配置，是解除城市缺水困扰的有效途径。由于我国北方城市缺水现象严重，尤其是北方沿海地区淡水资源的紧缺已经严重影响了城市的稳定发展，如何确定一个合理的供水结构，显得尤为重要。本文以极具代表性的青岛市为例，根据预测的该市供需水量，分别通过工程成本与全成本角度对各种供水水源、各种用户的费用效益进行量化对比分析，构建该市的水资源优化配置模型，在保证供给的情况下，使总体效益最大，得出其多水源多用户的联合优化方案，通过优化供水结构来解决该市的城市缺水问题。这也为我国其他城市特别是沿海缺水城市合理配置水资源提供了较好借鉴。本文在水资源优化配置过程中，对各水源各用户费用效益的取值，需要考虑的因素还有不完善的地方，这将有待于我们进一步的研究和探讨。

[1] Wong Hugh S,Sun Ne-zheng.Optimization of Conjunctive Use of Surface Water and Groundwater with Water Quality Constraints[C].Procedings of the Annual Water Resources Planning and Management Conference,1997:408-413.

[2] 吴泽宁,索丽生.水资源优化配置研究进展[J].灌溉排水学报,2004,23(2):1-5.

[3] 孙弘颜.长春市水资源系统的优化配置及策略研究[D].吉林大学,2007.

[4] Sakarya，A.Burcu Altan;Mays，Larry W.Optimal operation of water distribution pumps considering water quality[J].Journal of Water Resources Planning and Management.2000,126(4):233-239.

[5] Lnjayant C,Chieko U.Basinwide water management: a spatial mode[J].Journal of Envimonmental Economies and management,2003,(45):1-23

[6] 吴险峰,王丽萍.枣庄城市复杂多水源供水优化配置模型[J].武汉水利电力大学学报,2000,33(1):30-32.

[7] 吴英杰,刘廷玺,刘晓民.基于NSGA—Π算法的锡林浩特市多水源工业供水优化配置[J].中国农村水利水电,2010，(8):95-98.

[8] 岳春芳.东南沿海地区水资源优化配置模型及其应用研究[D].新疆农业大学，2004.

[9] 谷红梅,邱林,张民安等.渭南市供水水资源优化配置研究[J].人民黄河,2005，(12):55-57.

[10] 孙文,周芳红.渭南市城市水资源优化调度研究[J].甘肃科技,2006，(5):18-22.

[11] 叶健,刘洪波,闫静静.不确定性模糊多目标模型在生态城市水资源配置中的应用[J].环境科学学报,2012，(4):1001-1007.

[12] 王宏伟,张鑫.基于多目标遗传算法的西宁市水资源优化配置研究[J].水土保持通报,2012，(2):150-153.

[13] 张世坤.大连市水资源优化配置[D].大连理工大学，2006.

[14] 席清海,冯平.引黄济津应急调水的费用效益分析[J].天津大学学报(社会科学版)，2012，(5):396-400.

[15] 吴浩云,刁训娣,曾赛星.引江济太调水经济效益分析:以湖州市为例[J].水科学进展,2008，(6):888-892.

[16] 杜亚平,梅亚东,胡挺等.水资源多目标决策模型及其应用[J].中国农村水利水电，2012，(1):43-45.

[17] 孟庆才.青岛市各类水源全成本分析及供水结构优化研究[D].山东科技大学，2011.

AStudyoftheOptimizationofWaterSupplyBasedonVariousWaterSourcesandConsumersinCoastalCities

Gao Bo1, Guo Jü'e1, Xue Xinxi2

(1.School of Management, Xi'an Jiaotong University, Xi'an 710049, China;2.Qingdao Hairun Water Company, Qingdao 266002, China)

In view of various water sources and multi-industry users in urban water supply, an optimal allocation model should be designed from the perspective of the economic and social benefits.The article explores the optimization of water supply structure in a certain coastal city by analyzing various types of water resources engineering costs and total cost, and tries to find the best composite model in the development of water resources so as to maximize benefits of water supply, which will set an example of structure optimization of water resources for other similar cities.

water resources; optimal allocation; total cost

TU991

A

1672-335X(2013)02-0019-06

责任编辑：王明舜

2013-01-16

高波(1970- )，男，山东青岛人，西安交通大学管理学院博士研究生，专业方向为水资源管理与应用。