几种思想方法在数学分析教学中的应用
2013-10-29肖应雄
肖应雄
(湖北工程学院 数学与统计学院,湖北 孝感432000)
数学分析是高等师范院校数学教育专业的一门重要基础课。无论从知识结构的承前启后,还是从能力的培养和思维品质的提高诸方面看,数学分析教学对师范生的成长都起着十分重要的作用。由于数学分析中概念、定理比较多,因而光靠死记硬背是行不通的。针对这一现象,为了准确地掌握概念、定理,并熟练运用它们,就此列举了四种方法,即类比法、化归法、变式法和图象法。这些方法均可在数学分析课程教学中运用,包括在概念教学中的运用,在定理教学中的运用,在解题中的运用。在教学中巧妙地运用好这些方法,可以为学生探求知识发挥有效的作用。但也须注意,不可机械套用,把未经证明的结论当作真理。
1 类比法在数学分析教学中的应用
类比法(或称类比推理法)是指根据两个问题有一部分特征相类似,从而推出其他特征也可能相类似的一种推理方法。一般地,为了解决数学问题A,会联想一个已经会解的与A有某些类似特征的问题B。于是推测:
1)问题A与问题B有某些类似的结论。
2)用解决问题B的类似办法来解决问题A。
数学分析课程中能够运用类比法思考的问题是很多的,教师在讲授这门课时,不仅要传授知识,培养学生逻辑推理、逻辑论证的能力,还要注重类比法的应用,以培养学生的探究能力,进而提高学生的创造思维能力。
1.1 类比法在概念教学中的运用
数学概念是数学对象本质属性的抽象,因而概念的理解对于学生来说相对较难。而类比法非常具有启发性,因而数学分析中的许多概念可以通过类比法引出并揭示它的本质。
例如,对于二元函数极限的概念,学生理解起来比较困难,但是,学生对一元函数极限却比较熟悉。因而,可以在理解一元函数极限的基础上去理解二元函数极限,它们都是利用ε,δ语言描绘变量的变化过程,因而可类比地表述为:
一元函数的极限:设函数f在点x0的某个空心邻域U°(x0,δ)内有定义,A 为确定的实数。∀ε>0,∃δ>0,使得当x∈U°(x0,δ)时,有:|f(x)-A|<ε,则称函数f当x趋于x0时以A为极限,记作:(x)=A
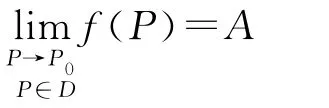
这种方法对概念的理解具有启发性,有利于学生对概念的理解,从此提出新的问题。
1.2 类比法在定理教学中的运用
数学分析中有很多内容是定理的证明与公式的推导,其中有许多定理是可以做互相类比的。通过类比逐步引导学生引出新定理的内容,从而做出推理论证。例如函数极限的性质和柯西收敛准则可通过与收敛数列的性质和柯西收敛准则进行类比,引出它的全部性质。无穷限广义积分通过与数项级数进行类比,引出它的全部敛散性理论。还有(x)g(x)dx与∑anbn都可用阿贝尔判别法判断它们的收敛性。
1)若{an}为单调有界数列,且级数∑bn收敛,则∑anbn收敛。
2 化归在数学分析教学中的运用
化归,从字面上看,就是转化和归结的意思。化归思想是指人们在研究问题时,把待解决的研究对象,通过某种转化过程,把它归结到另一类已经解决或比较容易解决的问题中去,最终使原问题得到解决的一种思维方法,是一种重要的数学思想方法。
化归思想在解决数学问题时经常用到。对未解决的问题作转化,使之归结为已经解决的问题,从而达到化繁为简、化难为易的目的,可以说解决数学问题的实质就是如何实现化归。在解题教学中,化归策略运用得当不仅可以使解题成功,而且有助于拓宽学生的视野,提高学生迅速解决问题的能力,培养学生的创新精神。
在数学分析解题中,化归思想的运用有两种形式:
1)判断问题,若P、Q是互相等价的命题,则判定P可归结为判定Q,反之亦然。
2)计算问题,若A、B是两个相等的量,则计算A可归结为计算B,反之亦然。
以上两种化归都是可逆的。在数学分析课程里,大量的数量关系都存在着可逆成分,因而数学分析中的很多问题都可以利用化归思想来解决。在解题过程中,若按照思维的习惯陷入困境时,可把思维转到另一逆方向,则更有利于问题的解决。但在具体运用时往往忽略这一方向的化归,有时正是由于这一方向的化归,往往会使人茅塞顿开,绝境逢生,使问题得到解决。
3 变式在数学分析中的应用
变式,是指在给学生提供范式的同时,通过变更问题的条件、方法、形式,使事物的非本质属性时隐时现,而事物的本质属性保持的变化方法。
变式有多种形式,它作为一种重要的教学途径,在实施变式教学时,可以引导学生对同一来源材料从不同角度、不同方位联想及思考问题,探求不同的解答方案,达到举一反三、触类旁通的效果,有利于学生发散思维的培养和提高。
3.1 形式变式在数学分析教学中的应用
在对一类探索性问题进行研究时,可以将条件和结论完整的题目改造成给出,先猜结论,再进行证明;也可以改造成给出结论,探索条件的条件;还可以将一类问题等效地叙述,即可以运用建模的方法,将一类实际问题抽象成形式化的数学问题。
例1 设函数f(x)在区间[-a,a](a>0)上连续,则:
通过形式变式:
形式一:如果f(x)在x0的某个邻域内连续,并且关于直线x=x0对称,证明∀a>0(x0+a,x0-a为邻域内的点),则有
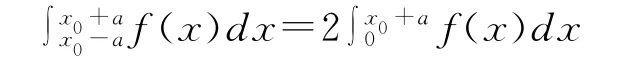
形式二:如果f(x)与g(x)在x0的某个邻域内连续,并且关于直线x=x0对称,证明∀a>0(x0-a,x0+a为邻域内的点),
则有

注:通过变式,对掌握积分的基本性质,简化一类积分运算具有重要意义。同时,也激发了学生的学习兴趣,培养和锻炼了学生研究学习的能力。
3.2 内容变式在教学中的应用
内容变式是指通过变更问题的条件、结论或关键数据而形成的一种形式类似解法或难度迥异的新题。根据需要,可将问题特殊化,也可一般化,通过内容变式,可帮助学生深刻领会问题的本质。
例2 给定两正数a1与b1(a1>b1),作出等差中项与等比中项,令an+1=
4 图象法在数学分析教学中的应用
在数学分析中我们常常会运用图形来解决一些不易解决的问题,从而使问题得以简化、直观化。
4.1 罗尔定理中的图象法
定理1 (Roll中值定理)若函数f满足如下条件:
ⅰ)f在闭区间[a,b]上连续
ⅱ)f在开区间(a,b)内可导
ⅲ)f(a)=f(b)
则在(a,b)内至少存在一点ξ,使得f
′(ξ)=0。
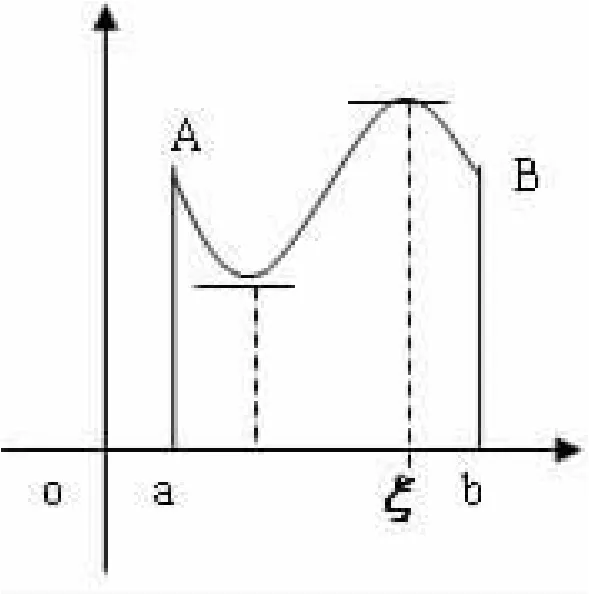
图1
几何意义:在每一点都可导的一段连续曲线上,如果曲线的两端点高度相等,则至少存在一条水平切线。
4.2 拉格朗日中值定理
定理2 (拉格朗日(Lagrange)中值定理)若函数f满足如下条件:
1)f在闭区间[a,b]上连续;
2)f在开区间(a,b)内可导,
则在(a,b)内至少存在一点ξ,使得

分析:在罗尔定理中由于f(a)=f(b),显然相应的线段AB平行于x轴,由此看出罗尔定理是Lagrange中值定理的特殊情况。将罗尔定理的图形旋转,即把弦AB绕其某一点旋转到不与x轴平行(A,B两点不在同一高度),就转化为Lagrange中值定理了。
下面我们就利用其图形的意义来证明一下。
证明一:如图1所示,作辅助函数
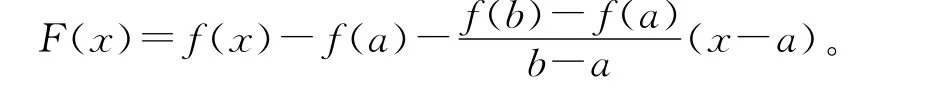
显然,F(a)=F(b)(=0),且F 在[a,b]上满足罗尔定理的另两个条件。故存在ξ(a,b),
使

即

获证!
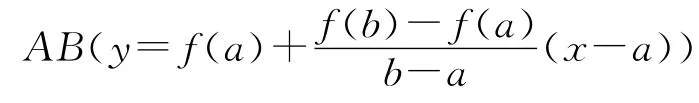
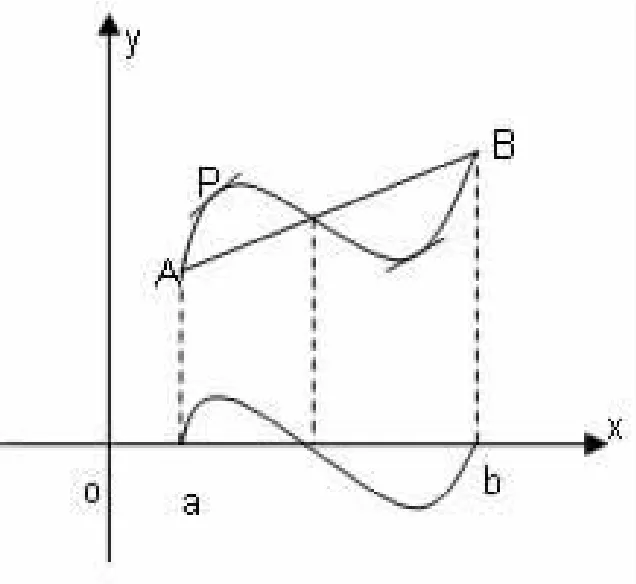
图2
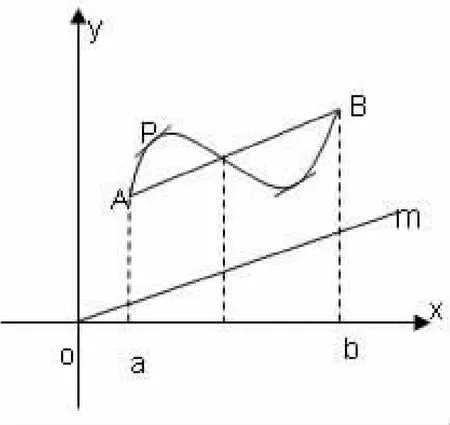
图3
证明二:如图2所示,构造辅助函数
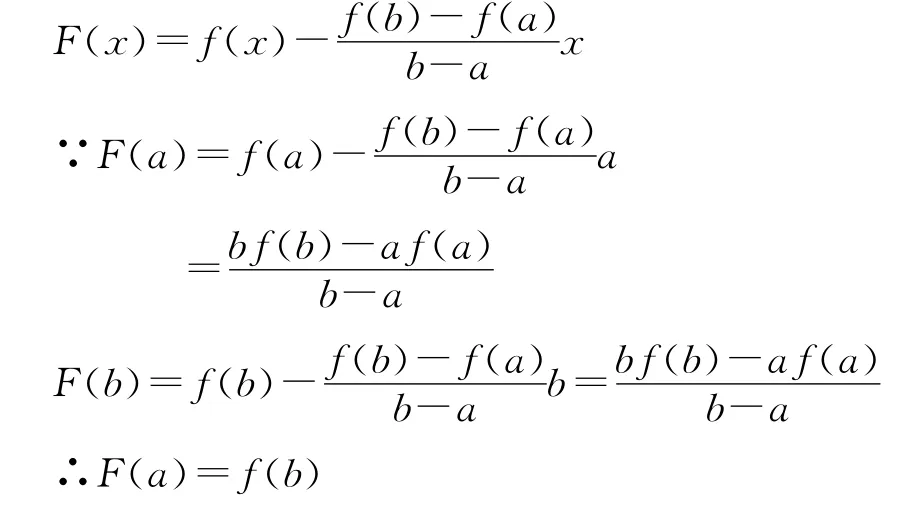
且F在[a,b]上满足罗尔定理的另两个条件。故存在ξ∈(a,b),
使
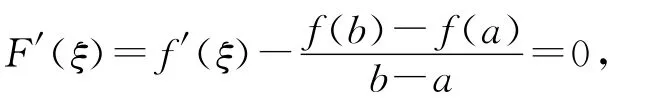
即

获证!
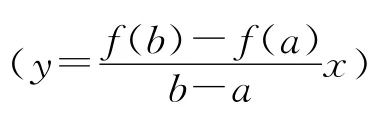
本文探讨了类比法、化归法、变式法和几何画图法在数学分析教学中的运用,在教学中灵活运用这些方法,可以大大提高学生对数学分析学习的效果。
[1]张秀全,赵文菊.数学分析教学中的若干问题探讨[J].天中学刊,2004,19(4):57-58.
[2]周景芝.数学分析教学中的若干意见[J].江苏连云港师范学院学报,2003,(1):89-92.
[3]贺海英.类比法在数学分析中的运用[J].伊犁教学学报,2001,14(6):68-71.
[4]林远华.化归思想在数学分析解题中的应用[J].河池师专学报:自然科学版,2002,22(2):20-23.
