地震学百科知识(五)
----地震各向异性*
2013-10-29张忠杰许忠淮
张忠杰 许忠淮
1) 中国科学院地质与地球物理研究所,北京 100029 2) 中国地震局地球物理研究所,北京 100081
1 基本概念
地震波在地球的各向异性介质中传播时,其传播速度与质点偏振方向等特性随波的传播方向而变化的现象,称为地震各向异性。
地震各向异性通常表现为三个方面:① 波的传播速度随传播方向而变化;② 波的传播速度随波动的质点偏振方向不同而发生改变;例如,S波经过各向异性介质后会分裂为以不同速度传播的快S波和慢S波,二者的偏振方向不同;③ 会发生波动质点的异常偏振,即在各向异性介质中波动偏振面通常既不平行于、也不垂直于波的传播方向。此外,地球介质的各向异性会使地球自由振荡的振型发生分裂。
2 理论
目前讨论介质的各向异性性质通常是指线性弹性介质的各向异性,理论上的描述是指联系应力张量σ和应变张量ε的弹性张量Λ在直角坐标(x1,x2,x3)下将采取更一般的形式
(1)
式中λijkl是4阶弹性张量Λ的分量,σij和εkl分别是2阶应力和应变张量的分量。(1)式可称为广义胡克定律。对均匀的弹性介质,弹性张量的各分量都是常数。弹性力学已证明,由于应力和应变张量的对称性及热力学定律的约束,对一般弹性体,(1)式中的弹性常数λijkl只有21个是独立的。
对各向同性弹性介质,弹性张量Λ只有两个独立分量,其余分量都是零。而对最一般的各向异性线性弹性介质,Λ有21个独立分量。但是,如果介质的各向异性还表现出一定的对称性,则独立的弹性常量还可减少。常见的情况有:① 如果弹性介质中存在相互正交的三个平面,弹性性质相对这些平面显示出对称性,则独立弹性常数减为9个,这种介质被称为正交各向异性介质。② 如果介质性质围绕空间的一个轴线是对称的,这时独立弹性常数只有5个,这种介质被称为六面体各向异性介质;当对称轴垂直于地表时,常称为横向各向同性介质。
为研究各向异性弹性介质中地震波的传播特征,可将(1)式代入无体力源项的运动方程而得到各向异性弹性介质中的波动方程。为求此波动方程的位移场的解答,常先假定可能解答具有单色平面波的形式
uj=ajei ω[t-(p1x1+p2x2+p3x3)/c],j=1,2,3
(2)
式中uj是位移矢量u的分量,ω是角频率,aj是偏振矢量a的分量,c是假定的平面波的传播速度,p1、p2、p3是波传播方向的单位矢量p的分量。
当将(2)式代入波动方程并经过微分运算后,将得到3个未知位移分量遵从的3元齐次代数线性方程组。为使位移分量有解,该方程组的系数行列式必须等于零;由于此行列式中包含未知的波速参数c,行列式为零的方程实际转化为波速c的高次代数方程,解此代数方程可得到波速c的3个可能解答。
进一步的理论分析结果预言,这3种波速对应于在均匀的各向异性弹性介质中传播的3种体波,它们是偏振方向相互正交的独立传播的波,分别称为准压缩波(记为qP)和2个准剪切波(分别记为qSV和qSH)。除了沿介质弹性的对称平面传播的特殊情况外,qP、qSV和qSH波的传播方向并不一定与各自的波阵面垂直。
这3种波的传播速度也是随空间方位而变化的。在弱各向异性(各向异性与各向同性的差异是高一级的小量)的假设条件下,假定波是在x1-x2平面内传播(图1),英国

图1
Crampin导出了以下波速平方随方位的变化[1]:
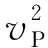
CCcos4θ+CSsin4θ

(3)
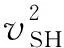
式中ρ是密度,θ是从x1轴向x2轴量至传播方向的方位角,vP、vSV和vSH分别是qP、qSV和qSH波的传播速度;式右端的其他常数和正弦、余弦函数的系数皆是介质各向异性弹性参数的简单代数组合值。由(3)式可见,qP波的速度随传播方位有π和(π/2)两种周期的变化,qSV波有π周期的变化,而qSH波有 (π/2)周期的变化。不同体波的波速显示出不同的方位变化,这是重要的地震各向异性特征。
除上述体波在各向异性介质中传播的基本理论外,已有人研究了面波在各向异性介质中的传播[2-3]、地震波在多层各向异性介质中的传播[4-5]等问题的理论。
此外,有人研究了地震波在各向异性介质中的激发问题[6]。研究结果指出,在各向异性介质中的纯平面剪切位错震源的地震波辐射不再完全等价于双力偶震源的辐射,体波辐射不再完全是四象限分布;虽然一般差异可能不太大,但对位错面的一些特定取向,差异会是相当大的。
3 研究简史
3.1 理论研究
地震各向异性现象早期是从理论研究开始的。19世纪中叶后,欧洲就有人开始了各向异性弹性介质的理论研究。已有专著指出[7],Christoffel有关各向异性弹性波传播特征的著作早在1877年就出版了。20世纪后,英国Love研究了横向各向同性介质中应力与应变的关系;随后又研究了横向各向同性介质中面波、体波的传播[8]。
20世纪60年代,地震波传播的各向异性效应相继在地震勘探和天然地震研究中被发现,之后,理论研究也进入相对活跃期。在众多研究中兹列举几例,如1961年Anderson提出了层状各向异性介质中的弹性波传播理论[9];为解释在海洋地区发现的Pn波速随传播方位变化的观测结果[10],1965年Backus给出了弱各向异性介质中P波速度随传播方位变化的理论表达式[11];1970年,英国Crampin首次计算了在水平各向异性地层中面波传播的相速度[2];1972年,Cerveny等人发展了2维非均匀各向异性介质中波动射线法正演模拟技术[12];1977年,Crampin和他的同事共同提出了多层各向异性介质中的地震记录合成的反射率法,并在人工地震深部地壳结构探测以及天然地震资料分析中得到应用[1]。
由于地震波在各向异性介质中的传播问题远比各向同性中的复杂,1980年代后,发展高效的合成地震图的算法成了理论地震学研究的一个热点问题[13-14]。此外,还有很多人研究利用体波或面波观测结果推断地球介质各向异性参数的反演方法。
3.2 观测研究
地震勘探学家首先观测到了地震各向异性现象。据报导,早在1932年就有人发现加拿大Lorraine地区页岩的P波水平向传播速度比垂直向速度快40%[15];1956年,有人在近地表沉积岩中观测到SH波的水平传播速度是垂直速度的两倍。
20世纪60年代后,地震各向异性的观测与解释研究得到显著发展,这主要得益于国际上大量的地壳、上地幔尺度地震探测及其后的地球动力学研究计划的开展。1964年Hess等发现了东太平洋一个大洋破裂带附近的Pn波速度的方位变化,并推断地震波速度的各向异性是海底扩张地震学的证据之一。随后太平洋地区进行的大量爆破地震研究结果证实了前述的观测与推断。1980年代后,大量宽频带地震仪的利用,S波、ScS波和SKS (PKS、SKKS)波分裂现象的发现,使上地幔的各向异性研究成为热点。1975年,Forsyth发现东太平洋脊附近地区的瑞利面波相速度有明显的方位变化[16];1991年Silver等人根据SKS和SKKS波的分裂分析,发现了北美、欧亚、非洲等大陆地区上地幔的各向异性特征[17]。此后,大量观测研究结果证实了上地幔介质存在各向异性。
1984年,Crampin提出了一个地壳介质在构造应力场作用下会产生定向裂隙略微张开的介质的扩容各向异性模型(作者称为EDA模型)[18],此后,出现了很多用近地震直达S波分裂研究地壳介质各向异性的结果[19,20],这些结果被认为与现今构造应力场的作用有关。由于岩层中的裂隙与油气的运移关系密切,这一模型在油气勘探中也有较广的应用。不过,由地震波观测到的地壳介质各向异性是单由现今构造应力作用的结果,还是也与以往的构造运动的结果有关,此问题还在研究之中。
在资源勘探领域,长期以来一直有大量的地震各向异性的观测和理论研究工作。例如油气勘探特别关注沉积岩层中的裂隙密度、取向和分布,它们会引起岩层显示出地震各向异性,许多人研究了如何能从地震勘探剖面资料或测井资料中有效提取出各向异性特征的方法。
20世纪90年代后,已有人注意到地震波衰减特性各向异性的研究。
4 S波分裂分析方法
S波分裂是指:当S波入射到各向异性介质后,会分裂为传播速度不同的快S波和慢S波,二者的偏振方向相互垂直,一般都与入射波的原始偏振方向不一样(图2)。除了测定地震体波和面波传播速度的方位变化外,观测S波的分裂现象是检测地球介质是否各向异性的常用方法。
有多种从S波地震记录确定S波分裂参数的方法,其中相关函数法和切向能量最小法较为常用。
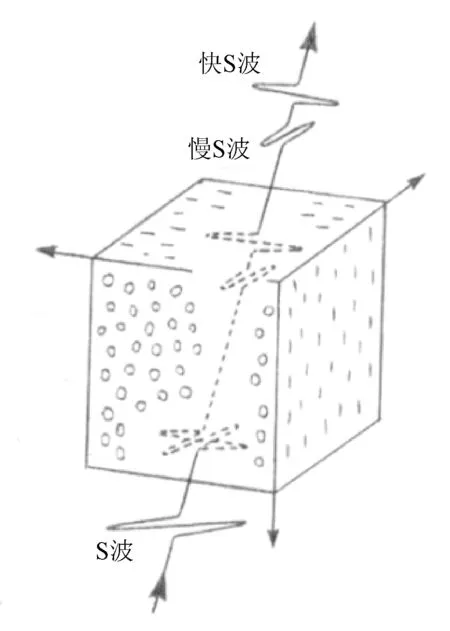
图2 S波入射到各向异性介质后分裂为快S波和慢S波示意图
4.1 相关函数法
快S波的偏振方向α(用与正北方向的夹角量度,图3)和慢S波相对快S波的时间滞后量δt称为S波的分裂参数。由于快、慢S波是从同一入射S波分裂出来的,在补偿了慢S波时间延迟的影响后,二者的波形应是相关的。
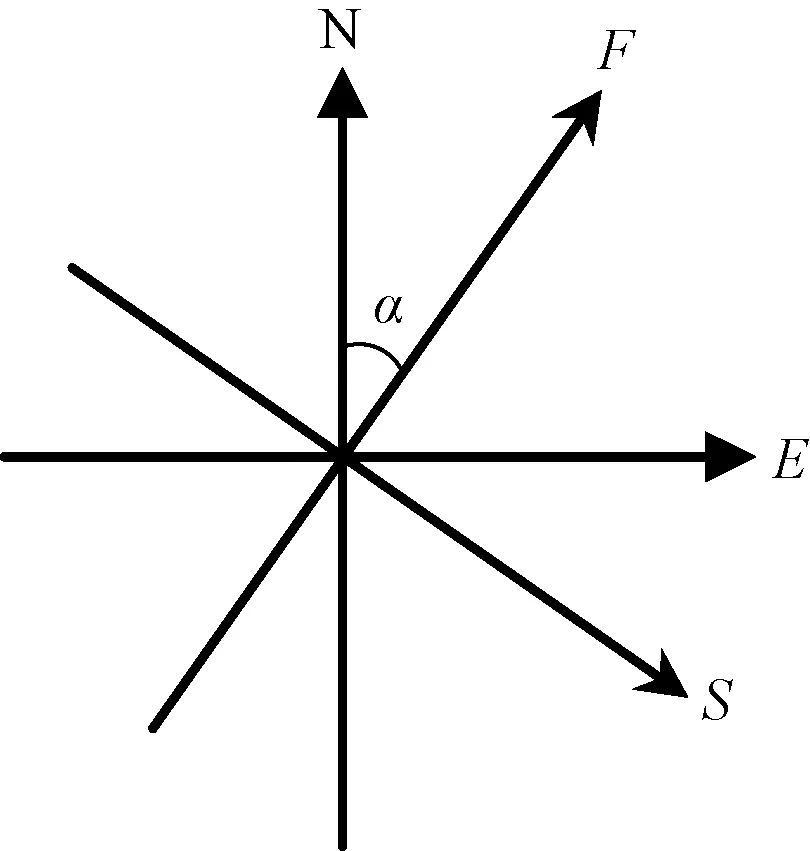
图3 分析S波记录的两个坐标系
假定初始S波是近垂直入射到地面台站的(多数情况这一条件能近似成立),则入射S波是在水平面内偏振的。可以将水平向S波的N--S向位移uN(t)和E--W向位移uE(t)记录重新投影到与原坐标夹角为α的F-S坐标系中而得到uF(t)和uS(t)(图3),如果F方向正好是快波偏振方向的话,则uF(t)将成为快S波记录,uS(t)将是有δt时间滞后的慢S波记录。这时,当考虑了慢S波有时间δt的提前后,计算的快、慢S波的互相关系数值

(4)
将有极大值,上式中t1和t2分别是所选S波震相记录的起始和截止时间。实际分析中是以一定步长变化(α,δt)的数对值,按(4)式计算与每个数对相应的相关系数C(α,δt);如果计算结果可找到C的单个的极大值Cmax,则说明可能确实存在S波分裂现象,与Cmax对应的(α,δt)就是所要求的S波分裂参数。
4.2 切向能量最小法
在研究地幔的各向异性时,多用较大远震的SKS震相记录作S波分裂分析。到达台站的SKS波是由P波在核-幔边界处转换成的S波(图4a),由于P波是在入射面内偏振的,如果地幔是各向同性的话,则SKS应是在震源至台站的入射大圆面内偏振的纯SV波,即它只有径向分量SKSR,而无切向分量。但实际地震记录经常观测到SKS的切向分量SKST(图4c),实际质点振动轨迹近似为椭圆形(图4d),而不是在径向线偏振的SV型振动。这说明地幔可能存在各向异性。
假定快波振动方向F与径向R的夹角为φ(图4b),慢波方向S与F垂直,则将R-T坐标下的振动改投影到F-S坐标下后,F方向将全是快波振动,S方向记录在经延迟时间δt校正后将全为慢波振动。由于这时S方向仅剩由地幔各向异性引起的慢波成份,不再含快波振动分量,因而这时切向振动能量将达最小。实际分析中是按一定步长用一系列(φ,δt)数对搜索使切向波动能量最小的F方向,而得到SKS波的分裂参数来。图4e是经过旋转和慢波延时校正后的F-S坐标下的记录,图4f是该坐标下的质点振动轨迹(接近线性偏振了)。
5 介质各向异性的成因
地球介质宏观各向异性的成因可归纳为固有各向异性与等效各向异性两大类。

图4 SKS波分裂分析示例。R表示台站的径向(沿大圆弧从震源指向台站的方向),T表示切向(垂直于R方向),F表示快波偏振方向,S表示慢波偏振方向。地震记录引自丁志峰等[21]
固有各向异性有两类。一类是源于矿物晶体本身的各向异性,一般认为地球介质的长期构造运动引起各向异性矿物晶体产生优势定向排列,从而形成了岩层的宏观各向异性。另一类是由于地下构造应力场作用的结果,例如应力场作用下岩层内部产生了定向排列的裂隙,造成岩层各向异性。
等效各向异性的成因较多,可主要列举以下几种:① 沉积岩层多有平行的层理结构,平行层理与垂直层理方向介质会显示不同性质;② 含有优势发育方向的裂缝、裂隙或节理等结构的岩层中,沿结构方向和横穿结构方向会显示出不同介质特性;③ 岩石中不同矿物颗粒的排列常有一定的顺序性,当顺序性的尺度远小于地震波波长时,会成为地震波速度各向异性的原因。
6 研究结果简介
现有研究已发现了地球的地壳、上地幔和内核部分有明显的地震各向异性;迄今尚未确认下地幔主体部分(不含核幔边界带)和液体外核存在显著的地震各向异性。

图6 中国东部SKS波分裂观测结果。各细棒表示快波偏振方向,中间圆点给出65个宽频带地震台的位置,棒长短表示慢S波延迟时间大小。兰色棒表示流动台阵台站的观测结果(引自文献[27])
6.1 地壳各向异性
大量地震勘探研究(包括井中勘探)发现了很多沉积岩层具有各向异性性质。
20世纪80年代后,一些研究者报导了基于天然近地震的数字地震记录、使用直达S波分裂分析技术推断出的地壳(主要是中上地壳)介质的各向异性特性。发现这些特性的地区主要是陆地的构造活动区,如美国加利福尼亚州的Imperial Valley地震区[19]、中国的北京附近地区[20]、希腊的Gulf of Corinth地区[22]等。许多研究者用Crampin提出的裂隙扩容各向异性模型来解释观测结果,以说明各向异性是与现今地壳的应力、应变特征有关的[18]。也有研究者[23-24]认为,它们可能与古构造运动有关。
6.2 上地幔各向异性
上地幔包含岩石层的底部和软流层,世界上对这里的地震各向异性是研究得最多的。主要观测依据有Pn波速度随方位的变化、面波传播速度随方位的变化、由大量宽频带数字地震台观测到的SKS波的分裂结果等。SH型的Love波传播速度比SV型的Rayleigh波传播速度快,这本身就说明在一定深度范围内的球面层中,波速是各向异性的。
图5给出全球上地幔地震各向异性研究结果的一种汇编。由图可见,大洋地区上地幔的各向异性程度一般比大陆地区的高;大陆地区(尤其是欧亚大陆地区)相对缺乏一致性的各向异性图像;快波速方向有从洋中脊指向板块俯冲带或大陆碰撞带的趋势。
对上地幔各向异性的解释多认为是由于橄榄岩中的橄榄石晶格的定向排列引起的,这支持上地幔存在长期的流动变形的观点。也有人认为观测到的各向异性既有岩石层中过去遗留下来的各向异性,也有岩石层中和软流层上层的现今动态变形引起的各向异性[26]。
图5中表示的中国及邻近地区SKS波分裂分析得到的快S波偏振方向(青色棒所示)似乎有点乱,这可能是前期研究结果的汇总。图6给出中国学者2009年对中国东部SKS波分裂的研究结果。由图可见,中国东北地区的快S波的优势偏振方向是NW--SE,向南到华北地区转为NWW--SEE,再到华南优势方向变为近E--W了。这一相对规则的快波偏振方向分布图像可能是中国东部地区的上地幔存在一定程度流动变形的迹象。
参考文献
[1]Crampin S. A review of the effects of anisotropic layering on the propagation of seismic waves. Geophys. J. R. Astron. Soc.,1977,49: 9-27
[2]Crampin S. The dispersion of surface waves in multilayered anisotropic media. Geophys. J. R. Astron. Soc.,1970,21: 387-402
[3]Montagner J P,Nataf H C. A simple model for inverting the azimuthal anisotropy of surface waves. J. Geophys. Res.,1986,91: 511-520
[4]Germany J. Seismograms in stratified anisotropic media. I. WKBJ theory. Geophys. J. R. Astron. Soc.,1988,92: 365-377
[5]Germany J. Seismograms in stratified anisotropic media. II. Uniformly asymptotic approximations. Geophys. J. R. Astron. Soc.,1988,92: 379-389
[6]Kawasaki I,Tanimoto T. Radiation patterns of body waves due to the seismic dislocation occurring in an anisotropic source medium. Bull. Seism. Soc. Amer.,1981,71: 37-50
[7]Babuška V,Cara M. Seismic Anisotropy in the Earth. Dordrecht: Kluwer Academic Publishers,1991
[8]Love A E H. A Treatise on the Mathematical Theory of Elasticity. Cambridge: Cambridge University Press,1927. Reprinted in 1944 by Dover Publications,New York
[9]Anderson D L. Elastic wave propagation in layered anisotropic media. J. Geophys. Res.,1961,73: 585-594
[10]Hess H H. Seismic anisotropy of the upper mantle. Nature,1964,203: 629-631
[11]Backus G E. Possible forms of seismic anisotropy of the uppermost mantle under oceans. J. Geophys. Res.,1965,70: 3429-3439
[12]Cerveny V. Seismic rays and ray intensities in inhomogeneous anisotropic media. Geophys. J. R. Astron. Soc.,1972,29: 1-13
[13]Gajewski D,Psencik I. Vertical seismic profile synthetics by dynamic ray tracing in laterally varying layered anisotropic structures. J. Geophys. Res.,1990,95: 11301-11315
[14]Babich V M. Ray method of calculating the intensity of wavefronts in the case of a heterogeneous,anisotropic,elastic medium. Geophys. J. Int.,1994,118: 379-383
[15]Levin F K. The reflection,refraction,and diffraction of waves in media with an elliptical velocity dependence. Geophysics,1978,43(3): 528-537
[16]Forsyth D W. The early structural evolution and anisotropy of the oceanic upper mantle. Geophys. J. Royal astron. Soc.,1975,43: 103-162
[17]Silver P G,Chan W W. Shear wave splitting and subcontinental mantle deformation. J. Geophys. Res.,1991,96: 16429-16454
[18]Crampin S,Evans R,Atkinson B K. Earthquake prediction: a new physical basis. Geophys. J. R. astron. Soc.,1984,76(1): 147-156
[19]Zollo A,Bernard P. S wave polarization inversion of the 15 October 1979,23: 19 Imperial valley aftershock: evidence for anisotropy and a simple source mechanism. Geophys. Res. Lett.,1989,16: 1047-1050
[20]高原,吴晶. 利用剪切波各向异性推断地壳主压应力场: 以首都圈地区为例. 科学通报,2008,53(23):2933-2939
[21]丁志峰,曾融生. 青藏高原横波分裂的观测研究. 地球物理学报,1996,39(2): 211-220
[22]Bouin M P,Tellez J,Bernard P. Seismic anisotropy around Gulf of Corinth,Greece,deduced from three-component seismograms of local earthquakes and its relationship with crustal strain. J. Geophys. Res.,1996,101: 5797-5811
[23]Blenkinsop T G. Correlation of paleotectonic fracture and microfracture orientations in cores with seismic anisotropy at Cajon Pass drill hole,Southern Califoria. J. Geophys. Res.,1990,95: 11143-11150
[24]Diagranes P,Kristoffersen Y,Karajev N. An analysis of shear waves observed in VSP data from the supperdeep well at Kola,Russia. Geophys. J. Int.,1996,126: 545-554
[25]Becker T W. Seismic anisotropy,in H.K.Gupta (Ch. Ed.),Encyclopedia of Solid Earth Geophysics. Springer,2011,1070-1081
[26]Cara M. Seismic anisotropy. In International Handbook of Earthquake and Engineering Seismology. Part A,Academic Press,2002,875-885
[27]常利军,王椿镛,丁志峰. 中国东部上地幔各向异性研究. 中国科学,D辑,2009,39(9): 1169-1178
