磁性层顶底埋深的功率谱计算方法及影响因素

杨 强，王有学，王海燕，周海滨

（1.广西隐伏金属矿产勘查重点实验室，广西 桂林 541004；2.桂林理工大学 地球科学学院，广西 桂林 541004；3.江西省核工业地质调查院，江苏 南昌 330038）

0 前言

确定磁性异常体的顶、底界面埋深是磁力勘探及解释的一个重要组成部分，目前主要采用特征点法、切线法、磁异常梯度的积分法、希尔伯特（Hilbert）变换法、矢量解释法以及磁异常快速自动反演方法和功率谱法对磁异常资料进行定量解释，进而求取磁源体参数。

功率谱法是确定磁性异常体的顶、底界面埋深时最常用的方法之一，该方法是由Spector和Grant［1］在频率域求解磁性体界面的平均深度时提出来的，其实质是“等效论”原理在磁法方面的应用。在较难进行工作的地区（如无人区或冻土区等），磁性体的磁化率等参数不易取得［2－3］，如果采用功率谱法就可以方便快捷地得到一个新区域的基底起伏、区域磁性层的顶、底界面深度等地质信息，为后续的地质工作提供有价值的参考资料。

作者在本文主要介绍利用磁异常及其垂向导数数据进行功率谱计算的方法和近似公式，此外还探讨了影响功率谱计算精度的一些因素。

1 基本原理

对于任意磁化的二度体（如图1所示），其垂直磁化强度Za的振幅谱公式为：

I为磁化倾角；J0为磁化强度；a为厚板的半宽度；h1为磁性体顶面埋深；h2为底面埋深。对式（1）进行傅里叶变换，得到Za的理论谱及功率谱分别为式（2）与式（3）。

其中 ω是圆频率。

图1 二度磁性体模型Fig.1 The model of 2－D magnetic body

1.1 磁性体顶深的确定

令h2＝h1＋△h，则式（3）可写成式（4）。

当｜ω△h｜≤1时，1－e－ω△h可以展开成级数，并取一级近似，可得式（5）。

对式（5）取对数，有：

lnP ＝ln｛［4πJ0△hsin（ωa）］2e－2ωh1｝并且令B ＝ln｛［4πJ0△hsin（ωa）］2｝，得：

从式（6）可以看出，在功率谱的低频段，二度磁性体顶面的埋深近似地与功率谱的对数呈线性关系，因此在lnP～ω的曲线上，可以利用低频段功率谱的斜率来确定二度磁性体顶面的埋深。

1.2 磁性体底深的确定

令e－wh1 ＝e－wh2＋w△h，带入式（3），得式（7）。

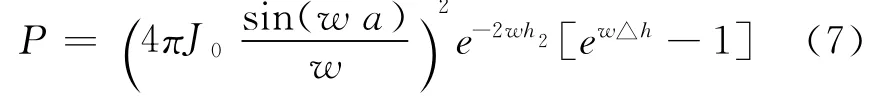
对式（7）取对数，得：

将ew△h－1展开成级数

在底面埋深公式的推导过程中，为了得到近似解，因此在级数中取其中某一项代替ew△h－1。

一般计算磁性体底深时，利用对数功率谱的低频段，近似的用级数中项ln［（w△h）3／6］来代替ln（ew△h－1）效果较好［4］。式（8）可以改写为式（9）。

令B′＝B＝2ln［（△h）3／6］，则：

计算磁性体底面埋深的公式如式（10）所示。在计算过程中需要注意的是，当△h的绝对值较大或较小时，式（10）可能存在比较大的误差（其相对误差一般均＜30%）。由此可见，利用功率谱法计算的磁性体底面埋深只具有一定的参考价值。

1.3 磁异常及其各阶垂向导数的功率谱计算埋深方法

联立引力位和磁位的泊松公式，可以导出功率谱利用磁异常和其各阶垂向导数异常数据计算磁性体顶、底界面埋深的公式，如式（11）、式（12）所示。

其中，上顶埋深为：

下底埋深为：

在式（11）和式（12）中，n≥0且n为整数，表示磁异常垂向导数的阶数；lnPn（w）表示磁异常第n阶垂向导数的功率谱［5］。

在此，使用磁异常的高阶导数进行功率谱的计算，是因为磁异常高阶导数比磁异常衰减的更快，所以在相同的区域内使用磁异常高阶导数计算功率谱，可以得到更高的计算精度［6］。

2 理论模型验证及讨论

为了检验功率谱法计算磁性体顶、底界面埋深的准确性及精度，设计了一系列不同几何参数的二度磁性体模型，并对其采用功率谱法计算模型的顶、底界面的深度，计算结果如表1所示。表1中分别给出了磁异常功率谱和利用垂向一阶导功率谱所计算的深度。可以看出基本能给出理想的计算结果。其中，2L为二度磁性异常体的厚度，即2L＝h1－h2。

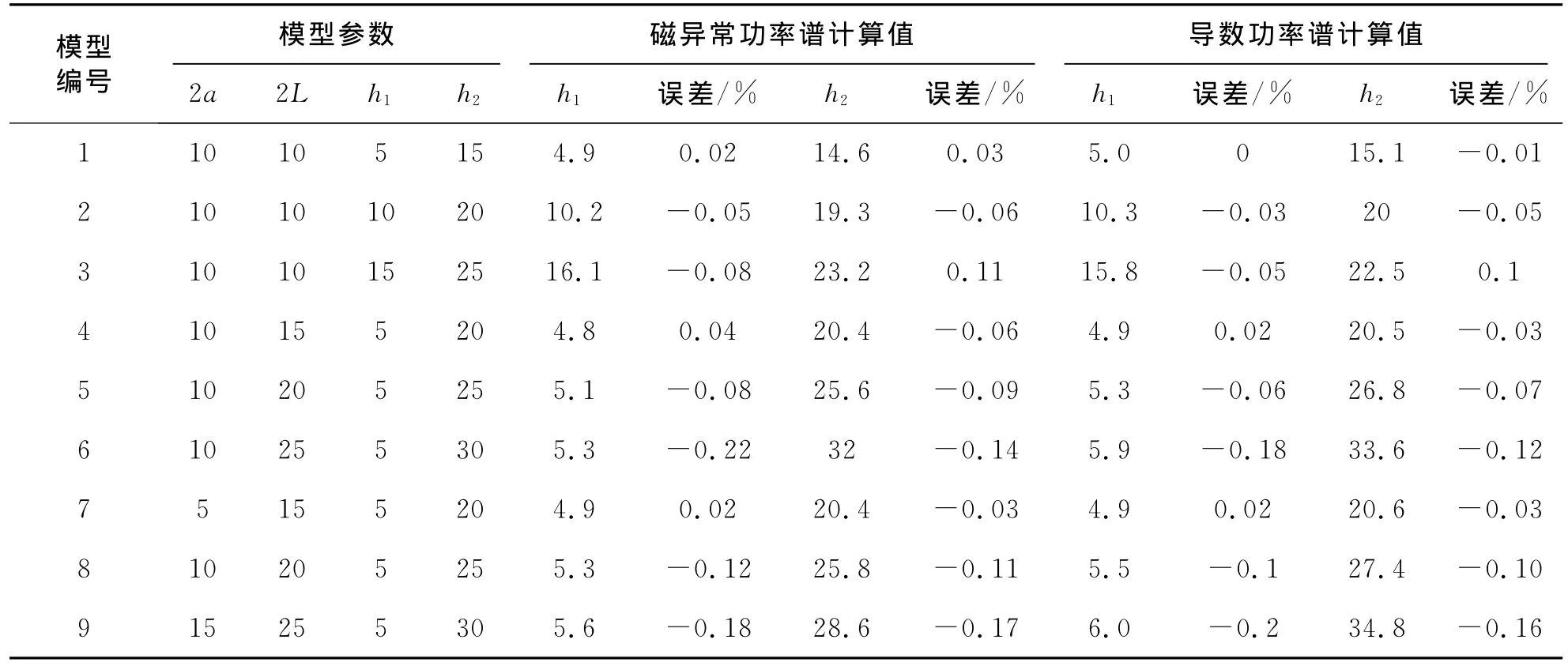
表1 不同a和L时磁性体顶底界面深度计算结果及误差对比Tab.1 Depth of the top and bottom when aand Lcalculated in different depth comparison and its contrast of errors

由表1可知，二度磁性异常体的宽度2a在计算顶、底界面埋深时没有太大的影响，但二度磁性异常体的顶面埋深h1和底面埋深h2对计算结果具有显著影响。当底面埋深h1较小时，计算出的底面埋深h2的精度比较好；而当计算顶面埋深h1时，在磁异常的厚度（2L）较大时精度稍差，其计算的误差最大为20%左右，基本符合要求。

在此设计一个磁性体的组合模型，以检验功率谱法对区域磁测资料的应用效果。磁异常组合模型示意图如图2所示。

图2是二度磁异常体组合模型的示意图，模型由八个柱体组成，其中顶面和底面均为变化的，顶面埋深在10m～20m之间，底面埋深在30m～40m之间。模型四周的空白为背景区域，可以看作是没有磁化或磁化率极低的围岩部分。

为了充分利用磁测数据及避免边界效应，通常采用“移动窗口”来计算整个区域，且每一“窗口”与下一个相邻“窗口”有50%的叠加部分，然后计算模型顶、底界面深度。图3为使用磁异常和其相应的垂向一阶导数异常数据进行功率谱计算得出的理论曲线和实际曲线的对比，从图3中可以看出，功率谱的计算结果误差较小，符合实际要求。

图2 磁性体组合模型的剖面示意图Fig.2 The section schematic of the combined magnetic models

由图3中的计算结果可以看出：在起伏界面的上凸点，导数谱的计算值比异常谱的计算值更接近一些，是因为对磁异常求取垂向导数后，得出的垂向导数异常分离了相邻磁性体之间的叠加效应，受到旁侧异常的影响较小；在界面下凹处，由于磁异常体的延伸较大，两种算法的结果与理论模型都非常接近，因此在使用一阶垂向导数数据计算磁性体界面埋深的结果中，其受到相邻磁性体影响较小的优点并不突出。然而，在磁异常转换为一阶导数异常时，由于数据转换处理必然会在原始数据中加入误差，所以最好能同时将磁异常的谱和其导数异常谱进行对比分析并结合使用，以便获得更加客观和合理的解释结果。

3 利用功率谱计算磁性体顶、底界面埋深的影响因素

通过分析功率谱法计算磁性体顶、底界面埋深的理论和近似公式［7］，在用模型验证的基础上，总结了在实际应用功率谱方法进行计算时需要注意以下几个影响因素：

图3 组合模型顶、底界面埋深计算结果剖面图Fig.3 The computed depths of the top and the bottom for the combined models

（1）磁性体底面埋深是在低频情况下求取的，但在计算时应尽量避免使用甚低频的点，以免使求取的界面深度具有较大的误差。

（2）利用功率谱求取界面深度时，“窗口”的选择对计算结果有很大影响。因为计算中使用的频谱的最低频是由“窗口”的大小来决定的，“窗口”与最低频呈反相关：“窗口”越小，最低频率越大；反之“窗口”越大，最低频率越小。磁性体底面底埋深是在低频段进行计算的，所以“窗口”的大小必须包括地质体的最低频谱［8－9］。

4 结论

作者在本文对功率谱利用磁异常及其垂向导数异常数据直接计算磁性体顶、底界面埋深方法，做了一定的介绍并分析了影响功率谱效果的因素。通过验证，可以肯定功率谱具有一定的优越性，具有实用价值。但是磁性体定量解释是一个复杂的问题，且磁异常功率谱在使用过程中人为选择的频谱和窗口有较大差异，磁异常的参量不同对功率谱的应用也会有一定的制约，需要在以后的研究中深入分析。

［1］SPECTOR A.GRANT F S.Statistical.models for interpreting aeromagnetic Data［J］. Geophysics，1970，35（2）：293－302.

［2］管志宁.地磁场与磁力勘探［M］.北京：地质出版社，2005.

［3］侯重初，李保国.直接计算磁性下界面深度的功率谱法［J］.物探化探计算技术，1985，7（2）：179－187.

［4］侯重初，李保国.计算磁性体上顶与下底深度的功率谱法［J］.物探化探计算技术，1985，7（4）：271－279.

［5］侯重初，李保国.利用位场及其高阶导数的功率谱计算岩层的深度与厚度［J］.地球物理学报，1988，31（1）：90－98.

［6］侯重初，杨全成.用谱分析建立一个位场反演系统［J］.物探化探计算技术，1990，12（4）：295－303.

［7］穆石敏，叶水盛.功率谱法估算埋深中的若干问题［J］.长春地质学院学报，1982，2（2）：95－102.

［8］王西文.对数功率谱法计算磁性体顶底深的若干问题［J］.西安地质学院学报，1989，11（4）：90－99.

［9］戴伟铭.利用功率谱直接求埋深的影响因素［J］.吉林大学学报：自然科学版，2010，40（增刊）：17－20.