多底井产能预测方法的分类与比较

杨青松，马 震 (中石油长庆油田分公司第一采气厂，陕西 榆林 718500)

王晓冬 (中国地质大学(北京)能源学院，北京 100083)

唐洪卫 (中石化西南油气分公司工程技术研究院，四川 德阳 618000)

安永生 (石油工程教育部重点实验室(中国石油大学(北京))，北京 102249)

李治平，苏 皓 (中国地质大学(北京)能源学院，北京 100083)

多底井产能预测方法的分类与比较

杨青松，马 震 (中石油长庆油田分公司第一采气厂，陕西 榆林 718500)

王晓冬 (中国地质大学(北京)能源学院，北京 100083)

唐洪卫 (中石化西南油气分公司工程技术研究院，四川 德阳 618000)

安永生 (石油工程教育部重点实验室(中国石油大学(北京))，北京 102249)

李治平，苏 皓 (中国地质大学(北京)能源学院，北京 100083)

多底井与常规水平井在产能预测方法上存在较大差异。国内外学者对其进行了大量研究，提出了一系列产能公式，其间经过不断改进和完善，使其接近于油田生产实际。从多底井产能预测的方法、多底井产能公式等方面阐述了国内外学者对多底井产能预测的研究历程，指出了不同产能公式的假设条件和适用范围以及各自的优缺点。

多底井;齐成伟;产能公式;解析法;拟表皮因子;半解析

多底井是指在油藏开发目的层中完井段以倾斜和多底为主要井眼轨迹特征的水平井，因为其特殊的井身结构对油藏渗流特征影响很大，使得多底水平井与常规水平井在产能预测方法上也存在较大差异，国内外学者对其研究的方法可以分为3种，即解析方法、拟表皮因子法和半解析法。解析方法利用共形映射、势叠加原理得到平面渗流场，再将互相垂直的2个平面渗流场架构为拟三维渗流场；拟表皮因子法修正表皮因子，在成熟的垂直井或水平井产能公式的分母中添加表皮因子；半解析法通过地层渗流和井筒流动的耦合，利用分段计算叠代产生。下面，笔者对国内外学者对多底井产能预测的研究情况进行阐述。

1 解析方法

1.1利用直井产能计算多底水平井产能

程林松等[1]利用替代比概念,提出了一种利用直井产能评价结果进行水平井产能评价的方法,并利用该方法对水平井及多底水平井的产能和影响水平井产能的因素进行研究，替代比的计算公式如下：

(1)

式中，R为替代比；re为泄油体半径，m；rw为生产段井筒半径，m；Sv为直井表皮系数；n为多底水平井的多底数；L为生产段井筒长度,m；β为渗透率各向异性系数；H为储层厚度,m；h为生产段井筒距储层底界的高度,m；SH为水平井表皮系数。

1.2用节点法计算鱼骨形多底井产能

何海峰等[2]提出了按井段划分流动段并用节点法计算多底井产能的方法。在总压差和油藏参数已给定的情况下，鱼骨形多底井的产能直接与多底井段内的压降有关，而这种压降又由水平井筒内的摩阻作用所引起。为便于计算多底井段内的压降，可将主井眼以多底位置分为若干段，将多底井眼与主井眼的交汇处记为节点。在遵守能量守恒和质量守恒的条件下，用水平井段流量分布计算方法，从水平井筒端点向出口处进行计算，就可以获得某生产压差下鱼骨形多底井的产能。

1)层流条件 层流条件下，产能计算公式为：

(2)

2)过渡流条件 过渡流条件下，产能计算公式为：

(3)

3)紊流条件 紊流条件下，产能计算公式为：

(4)

1.3不完全对称多井底水平井产能研究

彭昱强等[3]根据拟三维思想，运用保角变换以及镜像理论、叠加原理和等值渗流阻力法等渗流理论，对不完全对称多井底水平井稳定渗流进行了研究，推出其流场分布和产能计算公式。此外，还对影响不完全对称多井底水平井的部分参数进行了研究和分析，对多井底水平井的产能进行了比较。

不完全对称双底水平井的产能公式为：

(5)

式中，K为储层渗透率，10-3μm2；B为原油体积系数；L1为第一多底生产段长度，m；L2为第二多底生产段长度，m。

不完全对称四底水平井的产能公式为：

(6)

1.4 Табаков方法

Табаков利用下列方程计算对称式的多底水平井的产能[4]：

(7)

式中，F为支间干扰因子。当n=1、2、3、4时，对应的F=4、2、1.86、1.78。

式(7)的一个主要假设是所有的水平多底是在同一个点出去的，在实际的钻井操作中不存在上述情况。由于钻进半径的存在使得分离点和进入油层的点有一定的距离，该距离会对式(7)有一定影响。为此，Ramey对式(7)进行了修正并推导出下式[5]：

(8)

式中，m为不共点修正系数。

1.5保角变换结合镜像反映方法

程林松[6]等利用拟三维的思想，运用保角变换、镜像反映等处理方法将三维渗流问题转换为2个二维渗流问题，推导出了水平多底井的产能公式。后来，李璗等[7]从等值渗流阻力的角度、蒋廷学[8]利用保角变换，将多底井转换位单位圆也推导出了公式，证明了该公式的可靠性(见图1(a))。

齐成伟[9-13]考虑到多底水平井各分支生产段的不衔接情况，将分支裂缝群模型拓展为环形裂缝群模型，更加准确地描述了多底水平井的井身结构(见图1(b))。

齐成伟的圆形地层中辐射状多底水平井拟三维产能公式为：

(9)

式中，Kh为储层水平方向主渗透率，m2；si代表环形裂缝群的内接圆半径，m；so代表环形裂缝群的外接圆半径，m。

图1 多底水平井拟三维产能公式原型的改进(图中以3分支示意)

当si=0时，齐成伟公式退化为蒋廷学公式[8]；当n=1时，齐成伟公式退化为Joshi[14]或Борисов公式[15]。梁峰等[16]证实，程林松公式、王卫红公式[17]、李璗公式、蒋廷学公式[8]、冯文光公式[18]均为齐成伟公式的特例；邹丹等[19]证实，Борисов公式[15]、Giger公式[20]、Joshi公式、Renard&Dupuy公式[21]均是齐成伟公式的单分支退化公式。

1.6带形地层中多底水平井的产能研究

齐成伟于2009年继续发表了带形地层中横向水平井和纵向双底水平井的拟三维产能公式[22-24]。这是国内外首次出现的带形地层中的水平井产能公式。

齐成伟的带形地层中横向水平井(如图2所示，2个分支时的情形就是将2个带形地层并列靠在一起)的拟三维产能公式为：

(10)

式中，a为两供液边界的距离， m；b为带形地层的宽度，m。

陈德民等[25]证实渗透率各向异性带状水平地层中横向水平井拟三维产能公式在穿透比为1的退化情况下具有非常高的预测精度。陈元千等[26]将带形地层中横向水平井拟三维产能公式推广为带形低渗气藏中横向水平井的产能预测公式。

齐成伟的带形地层中纵向双底水平井(见图3)的拟三维产能公式为：

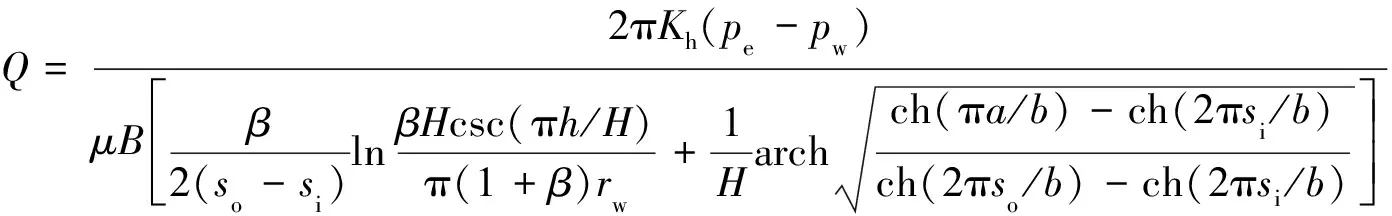
(11)

图2 带形地层中的横向水平井 图3 带形地层中的纵向双分支水平井

游支云等[27]根据齐成伟横向水平井和纵向水平井拟三维产能公式研究了带形地层中水平井方位对产能和采收率的影响。吕劲等[28]根据齐成伟横向水平井和纵向水平井拟三维产能公式对带状油气藏中的水平井方向进行了优选研究。张烈辉等[29]将齐成伟纵向双分支水平井拟三维产能公式推广为带状低渗透油气藏中纵向双分支水平井在不同完井方式下的产能公式。

需要注意的是，在应用上述公式计算多底井的产能时，泄油半径 是影响产能的主要因素之一，而该参数往往难以准确计算。为此，Joshi提出了等效泄油半径的概念[14]，其适用于水平多底点不同、有过渡段的情况；Chen[30]利用半数值解得到多底长度可以任意并且方向也可以任意的多底井的产能公式，但其前提条件是油藏形状有限制并且只是拟稳态时的解；S.J.Smith[31]对上述2种方法进行了实例对比。

解析法的优点是计算简单，但是其假设的条件过多，使其在实际生产中的适应性较差，如式(7)、(8)、(9)和(11)假设井为对称式的多底井，但是对称式的多底井是一种理想的多底井形式，在实际应用中很少，因而影响了上述公式的使用。同时，如泄油半径 等影响产能的重要参数很难准确计算出来，只能使用等效参数的概念，这也影响了计算结果的准确性。

2 拟表皮因子法

拟表皮因子法的主要特点是在均质等厚地层中，利用全渗透垂直井的线源解将任意的多底井用一口有综合表皮因子(拟表皮因子)的井代替，从而得到多底井的产能。假设条件如下：多底的方向是任意的、每个多底可以不在同一平面内、多底半径和表皮系数可以不同；每个多底都有无限导流能力而且在一个压力系统内，油藏简化为均质无限大平行平板，可以有各向异性的渗透率，流动为单相流动。Leif Larsen[32]提出了上述方法，具体内容如下。

拟稳态下采液指数的通用公式为：

(12)

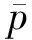
地层中任一点的压力计算公式为：

(13)

式中，角标D代表无因次的物理量；t代表时间，s。

对于无限大地层中任意多底井可以用下列公式表示井底流压：

(14)

对于一种特定的多底井，利用式(14)得到各自的井底压力(包含各自的表皮因子)，当满足式(13)所表示的压力分布的时候，就可以得到拟表皮因子的大小。

以双底井为例，文献[32]中给出了拟表皮系数的计算式为：

(15)

式中，S1为双多底水平井的表皮系数。

该方法的主要特点在于经过处理后的模型可以考虑多底之间隔离的情况，其优点是不针对特定的井型，对井的结构限制少，而且可以考虑每个多底表皮的影响，但该方法的不足是无法考虑边界和井筒中流动摩阻的影响。

3 半解析方法

3.1双多底井半解析计算法

韩国庆等[33]根据多层非均质油藏地层之间压力不平衡的特点建立了多底井半解析产能预测模型，包括油藏压力响应模型、井筒流动模型以及油藏渗流和井筒流动的耦合模型。该模型将油井分成若干段，对每一段进行油藏渗流和井筒流动的耦合，然后经过迭代求得每一段油井的压力和流入量分布，从而得到整个油井的产能。包括油藏压力响应模型、井筒流动模型以及油藏渗流和井筒流动的耦合模型。

3.2分离支半解析计算法

陈卫东等[34]提出了一种半解析法模型方法，即首先建立一个单支水平井模型，耦合地层渗流和井筒内的流动，计算出这个单支水平井的产能，在耦合和计算的过程中充分考虑摩擦压降、加速度压降和重力压降的影响。然后在一个多底油井中引入这个单支水平井的模型，从而计算出每个多底的产能、多底井的总产能以及井筒内的压降。

该半解析模型可以优化多底长度和纵向多底点的位置，但由于模型中没有考虑多底之间的相互影响，因此预测理想多底井结果较准确，但对于任意多底角度的多底(特别是多底角度较小时)或者鱼骨井产能的计算结果偏差较大。

3.3鱼骨井产能预测方法

范玉平等[35]、刘想平等[36]分别利用半解析模型建立了鱼骨井产能预测方法。刘想平把多底井各支沿其长度方向分成若干小段，假设从油藏流入每段内的流量沿该段长度方向为均匀分布，而各段流量不相等。根据镜象反映和势叠加原理可推导出各小段在油藏中产生的势，从而求出多底井在底水驱油层中任一位置产生的势，进而求得该点的压力，为计算多底上的产能打下基础。

这种方法的优点是考虑了多底角度对产能的影响；但叠加后的总产能没有考虑其它多底的存在对它的影响，导致计算出的单井产能要比实际要高。

3.4OuyangLiang-Biao方法

图4 多底分段示意图

Ouyang Liang-Biao[37]提出了一个多底井的井眼和油藏耦合模型，其主要假设是平行平板泄油体、微可压缩流体、多底井筒内考虑摩擦压降、加速度压降和重力压降，且多底形态可以是任意的(见图4)。

该方法的优点是先求得整个地层内的平均渗透率k*，在此基础上把井筒每个小段处的渗透率变化的影响转化为该小段的表皮因子s，因而处理结果有比较高的精度，但是该方法也没有很好解决多底井分支间互相干扰的问题。

3.5三维差分模型方法

在非常规井半解析模型方面，Wolfsteiner等[38]利用格林函数建立了直角坐标系下的三维差分模型，该模型考虑了井筒摩擦压降、重力压降和加速度压降，但存在如下不足之处：井筒流动模型和地层渗流模型中没有考虑完井方式的影响；对近井地带渗透率非均质性的处理没有考虑地层伤害的影响；没有考虑多底汇合处的局部压力损失的影响。

半解析方法的优点是简化了计算，又保证了一定的精度，但是该方法都不能很好的解决多底井分支间互相干扰的问题，而且解决两相问题也比较困难。

4 结论和建议

1)解析方法的优点是计算简单，但它假设条件过多，在实际生产中的适应性比较差；拟表皮因子法的优点是不针对特定井型，对井的结构限制少，其不足是无法考虑边界和井筒中流动摩阻的影响；半解析方法简化了计算，又保证了精度，但不能很好地解决多底井分支间的干扰问题，解决两相问题也比较困难。

2)目前研究多底井的产能，其泄油区域都是比较规则的圆形或带形，考虑更实际的泄油体几何形状是今后改进产能公式的发展方向。

3)考虑到多底井分支间互相干扰及多底长度影响也是今后研究产能公式时需要重视之处。

[1]程林松,李春兰.利用直井产能计算分支水平井产能的方法[J].大庆石油地质与开发,1998,17(3):27-31.

[2]何海峰,张公社,符翔,等.用节点法计算鱼骨形分支井产能[J].中国海上油气,2004,16(4):263-265.

[3]彭昱强,何顺利,魏俊之.不完全对称多井底水平井产能研究[J].大庆石油地质与开发,2003,22(2):28-30.

[4]Табаков. 平面地层分支水平井产量公式[A].全苏石油天然气科学研究院采油科技文集[C].ВНИИ:НТСПОДОБЫЧЕНЕФТИ，1961:61-65.

[5]Ramey Jr. Pressure Transient Analysis for Wells With Horizontal Drainholes[J].SPE15116,1986.

[6]程林松,李春兰,郎兆新,等.分支水平井产能的研究[J].石油学报,1995,16(2):49-55.

[7]李璗,王卫红,苏彦春.分支水平井产能的计算[J].石油学报,1998,19(3):89-92.

[8]蒋廷学.多分枝水平井稳态产能研究[J].特种油气藏，2000,7(3):14-17.

[9]齐成伟.环形裂缝群激发的渗流场之复分析[J].内蒙古石油化工,2009,35(21):39-40.

[10]齐成伟.裂缝激发的渗流场之运动学分析[J].内蒙古石油化工,2010,36(6):35-36.

[11]齐成伟.环形井群激发的渗流场之复分析[J].内蒙古石油化工,2010,36(22): 32-35.

[12]齐成伟.水平井渗流场的进一步探讨[J].内蒙古石油化工,2009,35(24):192-195.

[13]刘继林,杜殿发,黄世军,等. 拉格朗日描述在水平井渗流场中的应用探索——油气渗流力学教材增添内容之建议[J].内蒙古石油化工,2012,38(9):1-3.

[14]Joshi S D.Augmentation of well production with slant and horizontal wells[J].SPE15375,1988.

[15]БорисовoЮoП, ТабаковoВoП.有限厚度各向同性地层内的水平井和斜井的产量公式[A].全苏石油天然气科学研究院采油科技文集[C].ВНИИ:НТСПО ДОБЫЧЕ НЕФТИ,1964: 34-39.

[16]梁峰,孟维龙,刘晓辉.分支水平井产能方程式研究进展[J].石油钻采工艺,2010,32(5):64-68.

[17]王卫红,李璗.分支水平井产能研究[J].石油钻采工艺,1997,19(4):53-57.

[18]冯文光.油气渗流力学基础[M].北京: 科学出版社,2007.

[19]邹丹,梁峰,马强,等. 水平井与分支水平井产能公式的一致性分析[J].油气地球物理,2011,9(2):59-61.

[20]Giger F M. Horizontal wells production techniques in heterogeneous reservoir[J].SPE13710,1985.

[21]Renard G L, Dupuy J M.Influence of formation damage on the flowefficiency of horizontal well[J]. SPE19414, 1990.

[22]齐成伟,龙芝辉,汪志明,等.带形地层中裂缝激发的渗流场之复分析[J].内蒙古石油化工,2010,36(2):38-39.

[23]齐成伟,龙芝辉,汪志明.水平井流入剖面的简捷计算方法[J].石油钻探技术,2011,39(4):90-94.

[24]杨占伟,刘继林,杨刚,等.储层伤害下的低速非达西斜井产能分析[J].科学技术与工程,2012,12(25):6296-6299.

[25]陈德民,崔一平,高立超,等.分支水平井产能公式的精度分析[J].油气田地面工程,2011,30(3):15-17.

[26]陈元千,范子菲,游支云,等.带状低渗气藏中横向水平井的产能公式[A].第五届全国特种油气藏技术研讨会优秀论文集[C].沈阳：辽宁科学技术出版社,2012:528-531.

[27]游支云,苏堪华,郭晓乐,等.带形地层中水平井方位对产能和采收率的影响[J].特种油气藏，2012,19(4)：77-80.

[28]吕劲,郭伯云,游支云,等.带形油气藏中水平井方向优选研究[J].石油天然气学报(江汉石油学院学报),2012,34(5):103-106.

[29]张烈辉,熊友明,陈军,等.带状低渗透油气藏中纵向双分支水平井在不同完井方式下的产能公式[J].科学技术与工程,2012, 12(25):6454-6457.

[30]Chen W,Zhu D,Hil A D.Comprehensive Model of Multilateral Well Dliverability[J].SPE64751,2000.

[31]Smith SJ,Tweedie A A P,Gallivan J D.Evaluating the Performance of Multi_Lateral Producing Wells:Cost Benefits and Potential Risks[J].SPE38974,1997.

[32]Larsen L.Productivity Computations for Multilateral, Branched and Other Generalized and Extended Well Concepts[J].SPE36754,1996.

[33]韩国庆,吴晓东,陈昊,等.多层非均质油藏双分支井产能影响因素分析[J].石油大学学报(自然科学版),2004,28(4):81-84.

[34]陈卫东,Hill A D.多分支井产能预测方法[J].中国海上油气,2006,18(6):394-397.

[35]范玉平,韩国庆,杨长春.鱼骨井产能预测及分支井形态优化[J].石油学报,2006,27(4):101-104.

[36]刘想平,张兆顺.崔桂香,等.鱼骨形多分支井向井流动态关系[J].石油学报,2000,21(6):57-60.

[37]Ouyang Liang-Biao. A Simplified Approach to Couple Wellbore Flow and Reservoir Inflow for Arbitrary Well Configuration[J]. SPE48936,1998.

[38]Wolfsteiner C, Durlofsky L J,Aziz K.An Approximate Model for the Productivity of Non-Conventional Wells in Heterogeneous Reservoirs[J]. SPE56754,1999.

2012-11-12

国家科技重大专项(2011ZX05009)。

杨青松(1987-)，男，硕士，助理工程师，现主要从事油气水渗流力学、油气井产能预测、油气田开发方面的研究工作。

TE312

A

1673-1409(2013)08-N067-06

[编辑] 李启栋