单位球面上Möebius形式平行且仿Blaschke张量的特征值为常数的超曲面

邓义华

单位球面上Möebius形式平行且仿Blaschke张量的特征值为常数的超曲面

邓义华

(衡阳师范学院数学与计算科学系，湖南，衡阳 421008)

对超曲面的分类是Möebius几何中感兴趣的课题。本文研究了单位球面上Möebius形式平行且仿Blaschke张量的特征值为常数的超曲面的分类问题。运用Blaschke张量的特征值，本文得到了一类超曲面的Möebius形式平行与Möebius形式为零之间的一些关系。在此基础上将钟定兴、孙弘安2008年得到的Möebius形式为零时单位球面上超曲面的分类定理推广到了Möebius形式平行的情形。

仿Blaschke张量；Möebius形式平行；超曲面；Möebius不变量

1 单位球面上超曲面的Möebius不变量

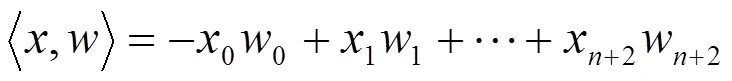
则结构方程的可积条件为：

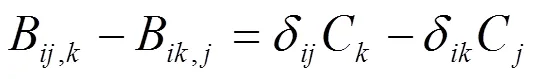
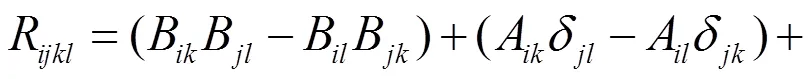
2 主要结论及其证明

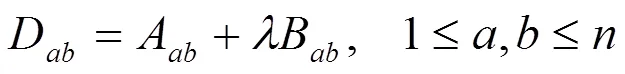
则有Ricci恒等式

由(1.3)与(1.5)式得

从而由(2.8)与(2.1)得

于是

由(2.1)、(2.3)和(2.13)式得

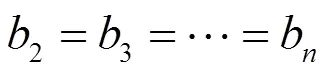
由(1.7)与(2.14)得

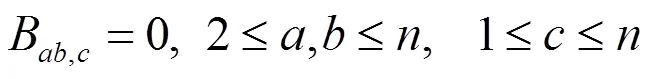
由(2.1)、(2.7)及(2.16)式得

又因为

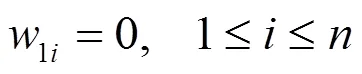
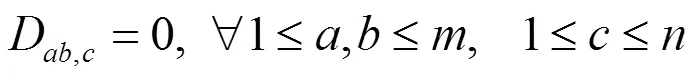
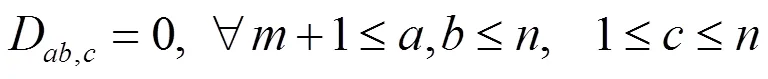
由定理2.1与定理2.2及定理A即可得到下面的分类定理：

则定理A的结论（i）和（ii）中必有一个成立。

[1] Liu H L, Wang C P, Zhao G S. Moebius isotropic submanifolds in Sn[J].Tohoku Math.J.,2001, 53: 553-569.

[2] 张廷枋. Sn+1中Moebius 形式平行的超曲面[J].数学进展，2003，32（2）：230-238.

[3] Li X X, Zhang F Y. A classification of immersed hypersurfaces in Sn+1with constant Blaschke eigenvalues[J]. Acta Mathematica Sinica: English Series, 2007, 23(3): 533-548.

[4] Li H, Wang C P. Moebius geometry of hypersurfaces with constant mean curvature and constant scalar curvature[J]. Mamuscripta Math., 2003, 112: 1-13.

[5] 夏巧玲. 关于具有常平均曲率和数量曲率超曲面的Moebius几何的一个注记[J]. 数学进展， 2006，35（6）：677-684.

[6] 钟定兴，孙弘安，张廷枋. S5上仿Blaschke张量的特征值为常数的超曲面[J]. 数学学报，2010,53（2）：263-278.

[7] 钟定兴，孙弘安. 单位球面上仿Blaschke张量的特征值为常数的超曲面[J].数学学报，2008，51（3）：579-592.

[8] Wang C P. Moebius geometry of submanifolds in Sn[J]. Mamuscripta Math., 1998, 96: 517-534.

THE HYPERSURFACES WITH PARALLEL MOEBIUS FORM AND CONSTANT PARA-BLASCHKE EIGENVALUES IN UNIT SPHERES

DENG Yi-hua

( Department of Mathematics and Computing Sciences, Hengyang Normal University, Hengyang, Hunan 421008 , China)

It is interesting to classify hypersurfaces in Möebius geometry. We focus on the classification of hypersurfaces with parallel Möebius form and constant Para-Blaschke eigenvalues in unit spheres. Some relations between a class of hypersurfaces with parallel Möebius form and wanishing Möebius form are obtained based on Para-Blaschke eigenvalues. Furthermore, a theorem obtained by Zhong and Sun in 2008 on the classification of immersed hypersurfaces with wanishing Möebius form is generalized to the immersed hypersurfaces with parallel Möebius form in unit spheres.

Para-Blaschke tensor; parallel Möebius form; hypersurfaces; Möebius invariants

O186.12

A

10.3969/j.issn.1674-8085.2013.01.001

1674-8085(2013)01-0001-04

2012-09-18；

2012-12-06

湖南省自然科学基金项目(09JJ6004); 湖南省教育厅优秀青年项目(08B010)

邓义华(1971-)，男，湖南郴州人，教授，硕士，主要从事微分几何研究(E-mail: dengchen4032@126.com).