构造
——数学竞赛解题的“钥匙”
2013-10-26
●
(松江区第二中学 上海 201600)
构造
——数学竞赛解题的“钥匙”
●缪雪松
(松江区第二中学 上海 201600)
“问题是数学的心脏”,数学离不开问题的解决.就数学竞赛活动而言,学生在学习数学竞赛知识、掌握数学竞赛技能、领悟数学竞赛思想的过程中,需要解决大量的数学问题.学生独立地分析、解决数学问题的过程,无论是真创造还是类创造,都是一个创造的过程,这样的过程对学生创新能力、实践能力的培养大有裨益.学生在解决数学竞赛问题的过程中,常常会遇到一道道的“关卡”,而“构造”这一策略,便成了突破解题障碍、打通道道“关卡”的神奇钥匙.在复杂的问题背景下,抽取问题的本质属性,寻找到数学知识内在的联系,常常能创造性地构造出新的、简单的数学模型,从而得到原问题的奇思妙解,这就是“构造”的精髓.
本文拟从以下7个方面向读者展现“构造”的无穷魅力.
1 构造代数式
例1已知a+b+c=a2+b2+c2=2,求证:
a(1-a)2=b(1-b)2=c(1-c)2.
分析求证的等式中的各式,恰好是多项式x(1-x)2中的x分别取a,b,c时的值.因此,本题可转化为证明当x分别取a,b,c时,x(1-x)2的值不变.由于x(1-x)2是关于x的三次多项式,且注意到题设条件,因此可构造三次式(x-a)(x-b)(x-c),建立它与x(1-x)2之间的某种关系.
证明因为
(a+b+c)2=a2+b2+c2+2ab+2bc+2ca,
又
a+b+c=a2+b2+c2=2,
所以
4=2+2ab+2bc+2ca,
从而
ab+bc+ca=1.
于是
(x-a)(x-b)(x-c)=
x3-(a+b+c)x2+(ab+bc+ca)x-abc=
x3-2x2+x-abc,
即
x(1-x)2=(x-a)(x-b)(x-c)+abc.
由此可见,当x分别取a,b,c时,x(1-x)2的值都是abc,因此a(1-a)2=b(1-b)2=c(1-c)2.
评注本题构造了三次式(x-a)(x-b)(x-c),然后建立它与x(1-x)2之间的关系,再通过赋值来证明.
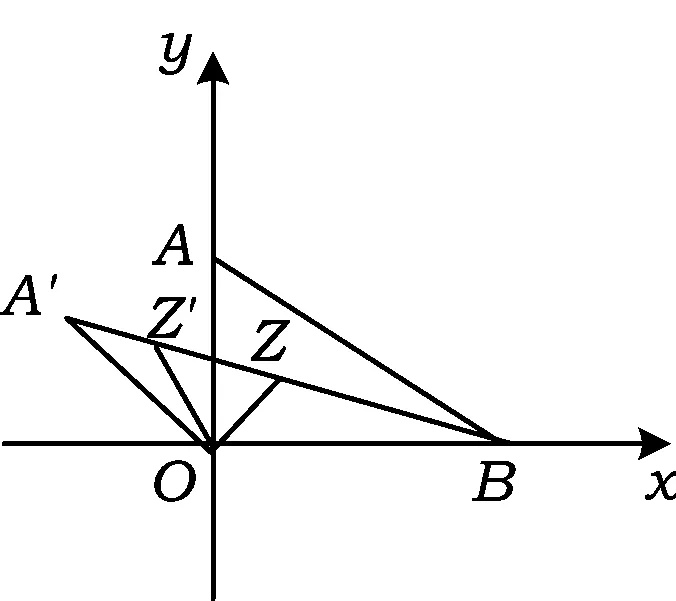
图1
2 构造复数

解设厂址的位置为Z,则Z到3个村庄的供水管道长为
d= |OZ|+|AZ|+|BZ|=







评注本题也可直接利用费马点的有关结论处理.
3 构造数组
例3已知集合A中有49个正整数,它们的约数都是不大于10的质数.求证:其中必有4个整数的乘积是一个整数的4次方.
证明A中的任一元素必可以表示为xi=2αi3βi5γi7δi(i=1,2,…,49)的形式,记xi=(αi,βi,γi,δi),当且仅当xi=(αi,βi,γi,δi)与xj=(αj,βj,γj,δj)中各个坐标的奇偶都相同时xi·xj=y2(其中y是正整数),而各坐标的奇偶不全相同的数组最多有24=16个.由抽屉原理可知,每17个不同数组中至少有一对数组对应奇偶均相同.
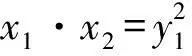
显然,y1,y2,…,y17这17个数都可以表示成2αi3βi5γi7δi的形式,在y1,y2,…,y17这17个数中,必存在2个数ym,yn满足ym·yn=p2(p为正整数),则与ym,yn对应的集合A中的4个元素之积即为p4.
4 构造关系
例4已知{a1,a2,…,a2 013}是由2 013个质数构成的集合,b1,b2,…,bn∈{a1,a2,…,a2 013},则乘积b1b2…bn共有多少个不同的值?
解法1(构造不等关系)
不妨设b1≤b2≤…≤bn.原问题等价于:求满足b1,b2,…,bn∈{1,2,…,2 013}的数组{b1,b2,…,bn}的个数,构造
1≤b1 解法2 (构造顺序关系,即隔板法) 原问题等价于:将编号为1,2,…,n的小球放入编号为1,2,…,2 013的盒中,要求序号大的球放入盒子的编号不小于序号小的球放入盒子的编号,求放法的总数. 例5把△ABC的各边n等分,过各分点分别作各边的平行线,得到一些由三角形的边或这些平行线所组成的平行四边形,试计算这些平行四边形的个数. 图2 解根据对称性,可先考虑边不平行于BC的小平行四边形.如图2所示,把AB和AC各延长一等分至点B′,C′,联结B′C′.将与AB′平行的n条线分别延长,与B′C′相交得到n个交点,这n个交点与点B′,C′作为线段B′C′的n+2个分点,从点B′至点C′依次记为1,2,…,n+2.图2所示的小平行四边形所在4条直线分别交B′C′于点i,j,k,l.记A={边不平行于BC的小平行四边形},B={(i,j,k,l)|1≤i 例6已知a1+a2+a3=b1+b2+b3,a1a2+a2a3+a3a1=b1b2+b2b3+b3b1,min{a1,a2,a3}≤min{b1,b2,b3},求证:max{a1,a2,a3}≤max(b1,b2,b3). (2008年北京大学自主招生试题) 证明设a1+a2+a3=b1+b2+b3=-A, a1a2+a2a3+a3a1=b1b2+b2b3+b3b1=B, 且不妨设a1≤a2≤a3,b1≤b2≤b3,设 f(x)= (x-a1)(x-a2)(x-a3)= x3+Ax2+Bx+C1, g(x)= (x-b1)(x-b2)(x-b3)= x3+Ax2+Bx+C2. 因为a1≤b1,f(a1)=0,而g(a1)≤0,所以C2≤C1.又f(a3)=0,于是 g(a3)=f(a3)+C2-C1≤0, 即 (a3-b1)(a3-b2)(a3-b3)≤0. 若a3>b3,则g(a3)>0,矛盾.因此a3≤b3,即 max{a1,a2,a3}≤max{b1,b2,b3}. 图3 例7在一圆周上任取3个点构成三角形,求该三角形是锐角三角形的概率. 解设圆半径为1,设3个顶点将圆分得的3条弧弧长分别为x,y,z,则x+y+z=2π,其中0 [1] 缪雪松.中国大学自主招生数学补充教程[M].北京:中国出版集团现代教育出版社,2012.
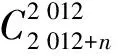
5 构造映射
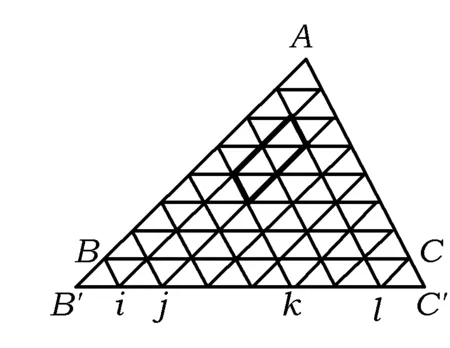
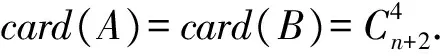
6 构造函数
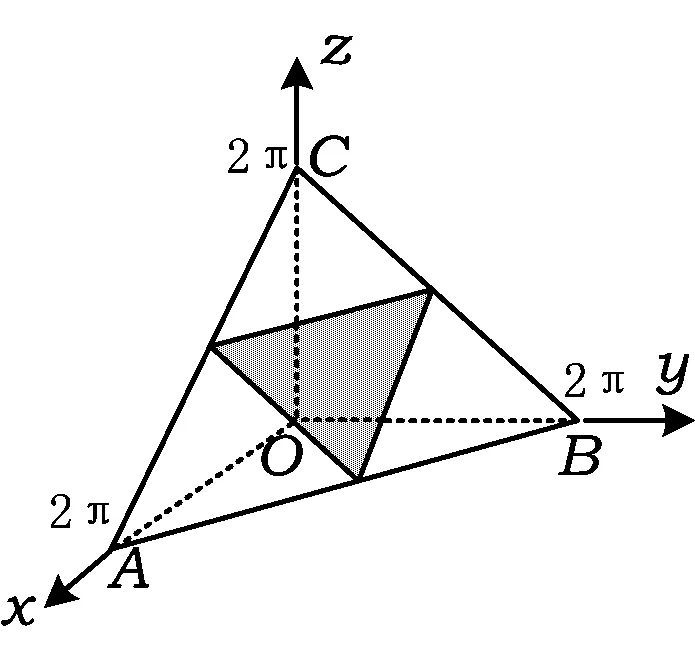
7 构造几何体

