不定方程问题的常见类型及其常用策略
2013-10-26
●
(镇海蛟川书院 浙江宁波 315201)
不定方程问题的常见类型及其常用策略
●刘清泉
(镇海蛟川书院 浙江宁波 315201)
不定方程是指未知数的个数多于方程个数,且未知数受到某些限制的方程或方程组.不定方程是初中数学竞赛中的重要内容之一,也是各级各类数学竞赛试题中的热点内容之一,求解时不但涉及方程(组)的相关知识,还涉及数论的相关知识,灵活性较大,技巧性较强.其中一些常见的问题,其解决策略往往与其呈现方式直接相关,笔者以其在初中数学竞赛中的常见类型进行分类,例析对应的解决策略.
1 一次不定方程
1.1 整体求解
例1母亲节到了,小红、小莉、小莹到花店买花送给自己的母亲.小红买了3枝玫瑰、7枝康乃馨、1枝百合花,共付了14元;小莉买了4枝玫瑰、10枝康乃馨、1枝百合花,共付了16元;小莹买上面3种花各2枝,则她应付________元.
(2010年天津市初中数学竞赛试题)
解设玫瑰、康乃馨、百合花的单价分别为x,y,z(单位:元),则
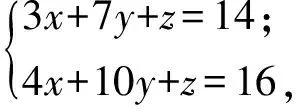
解得

从而 2(x+y+z)=2(2-3y+y+8+2y)=20.
评注因为x,y,z不能被唯一确定,所以利用消元思想将“三元”转化为“一元”,进而整体求解.本例亦可用下面的方法求解:
设m(3x+7y+z)+n(4x+10y+z)=2(x+y+z),则
(3m+4n)x+(7m+10n)y+(m+n)z=2x+2y+2z,
得
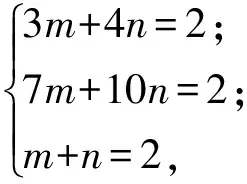
解得
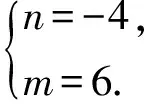
因此
2(x+y+z)= 6(3x+7y+z)-4(4x+10y+z)=
6×14-4×16=20.
1.2 设而不求
例2一辆客车、一辆货车和一辆小轿车在一条笔直的公路上朝同一方向匀速行驶.在某一时刻,客车在前,小轿车在后,货车在客车与小轿车的正中间;过了10 min,小轿车追上了货车;又过了5 min,小轿车追上了客车;再过了tmin,货车追上了客车,则t=________.
(2010年全国初中数学联赛试题)
解设在某一时刻,货车与客车、小轿车的距离均为Skm,小轿车、货车、客车的速度分别为a,b,c(单位:km/min).由题意得
由式(1)和式(2),得
30(b-c)=S,
结合式(3),得
t=30-10-5=15.
评注本例用增元法建立追击问题的模型,构造不定方程后,以求其中的“t”值为目标进行等式变形.
2 二次不定方程
2.1 形如“□xy+□x+□y+□=0”的二次不定方程
例3已知直角三角形的边长均为整数,周长为30,求该三角形外接圆的面积.
(2012年全国初中数学联赛试题)
解设直角三角形的3条边长分别为a,b,c(a≤b a2+b2=c2. 把c=30-a-b代入,化简得 ab-30(a+b)+450=0, 从而 (30-a)(30-b)=450=2×32×52. 由a,b均为整数且a≤b<14,知30-a,30-b均为大于16的正整数,从而 评注该类型比较常见,通常将等式左边因式分解、等式右边分解质因数,利用整数的性质求解.本例中将a,b排序,并挖掘30-a,30-b的特征是常用的解题技巧. 2.2 形如“□2-□2=□”的二次不定方程 例4若100a+64和201a+64均为4位数,且均为完全平方数,则整数a的值为________. (2007年全国初中数学联赛试题) 解设100a+64=m2,201a+64=n2,其中32≤m<100,32≤n<100,两式相减,得 101a=n2-m2=(n+m)(n-m). 由于101是质数,且-101 n+m=101, 故 a=n-m=2n-101. 代入201a+64=n2,整理得 n2-402n+20 237=0, 解得 n=59或n=343(舍去), 因此 a=2n-101=17. 评注本例从完全平方数切入构造不定方程,借助“平方差公式”,在“101是质数”的前提下,寻求a,m,n之间的线性关系,进而求解. 2.3 形如“□2+□2=□”的二次不定方程 例5关于x,y的方程x2+y2=208(x-y)的所有正整数解为________. (2008年全国初中数学联赛试题) 解因为208是4的倍数,又偶数的平方数除以4所得的余数为0,奇数的平方数除以4所得的余数为1,所以x,y都是偶数. 设x=2a,y=2b,则 a2+b2=104(a-b), 同上可知,a,b都是偶数.设a=2c,b=2d,则 c2+d2=52(c-d), 因此c,d都是偶数.设c=2s,d=2t,则 s2+t2=26(s-t), 于是 (s-13)2+(t+13)2=2×132, 其中s,t都是偶数.于是 (s-13)2=2×132-(t+13)2≤2×132-152<112. 不难确定|s-13|=7,从而 故 评注对于形如“□2+□2=□”的二次不定方程,若等式右边的常数为0或较小,可利用完全平方数的特征求解,或利用主元法转化为一元二次方程用判别式求解.由于本例中等式可化为 (x-104)2+(y+104)2=2×1042=21 632, (4) 其右边的常数较大,故利用奇偶分析法将其转化为等式右边常数较小的情形进而求解.当然,对式(4)亦可结合“完全平方数的尾数特征”分析求解,这里不再赘述. 2.4 转换主元解二次不定方程 例6不定方程3x2+7xy-2x-5y-17=0的全部正整数解(x,y)的组数为 ( ) A.1 B.2 C.3 D.4. (2013年全国初中数学联赛试题) 解由3x2+7xy-2x-5y-17=0,得 又x≥1,y≥1,则 -3x2+2x+17≥7x-5, 即 3x2+x≤22. 不难确定正整数x=1或x=2,从而(x,y)=(1,8)或(x,y)=(2,1).故选B. 评注本例中的不定方程关于“x”是二次的,关于“y”是一次的,则y可用x表出,在正整数解要求的前提下,在限定x取值范围的基础上,确定x可能的取值,进一步验证得到结论.事实上,本题求解时,很容易以“x”为主元,转化为一元二次方程的整数根问题进行求解,很多与二次不定方程相关的问题常常用到解决一元二次方程的整数根问题的相关策略,本文不再赘述. 2.5 与质数相关的二次不定方程 例7设a为质数,b为正整数,且9(2a+b)2=509(4a+511b),求a,b的值. (2008年全国初中数学联赛试题) 解由于9和509互质,则 509|(2a+b)2, 又509为质数,则 509|2a+b. 可设 2a+b=509x(x为正整数), (5) 则 9×(509x)2=509(4a+511b), 即 9×509x2=4a+511b. (6) 式(5)和式(6)消去b,得 x(511-9x)=2a. 由于a为质数,从而x=1或x=2或x=a.经检验,只有当x=1时,a=251,b=7,满足题意. 评注通常与质数相关的问题包括不定方程问题,应把解决整除、互质、质数与合数等问题的相关方法作为首选. 2.6 无解的二次不定方程 例8关于m,n的方程5m2-6mn+7n2=2 011是否存在整数解?若存在,请写出一组解;若不存在,请说明理由. (2011年北京市初中数学竞赛试题) 解(1)若m,n同奇偶,则原方程左边为偶数,不可能等于2 011. (2)若m,n异奇偶,把原方程可化为 (5m-3n)2+26n2=10 055, 其中5m-3n为奇数,(5m-3n)2=1(mod 8). ①当n为偶数时,26n2=0(mod 8),而10 055=7(mod 8),显然等式不成立; ②当n为奇数时,26n2=2(mod 8),而10 055=7(mod 8),显然等式不成立. 综上所述,方程5m2-6mn+7n2=2 011不存在整数解. 评注不定方程是否存在整数解也是不定方程的重要内容.解答时,常常借助奇偶分析,特别是对于二次不定方程,经常用到:(2n)2=0(mod 4),(2n+1)2=1(mod 8)(其中n为整数).更一般地,借助取模等方法探究是否有整数解,该方法也同样适用于其他形式的不定方程求整数解. 3.1 三次不定方程 例9已知a是正整数,如果关于x的方程x3+(a+17)x2+(38-a)x-56=0的根都是整数,求a的值及方程的整数根. (2007年全国初中数学联赛试题) 解由题意,得 x3+17x2+38x-56+ax(x-1)=0, 即 (x-1)[x2+(a+18x)+56]=0. 关于x的方程x2+(a+18)x+56=0一定有2个不相等的实整数根,则Δ=(a+18)2-224是完全平方数.设(a+18)2-224=k2(k为非负整数),则 (a+18)2-k2=224, 即 (a+18+k)(a+18-k)=224, 其中a+18+k与a+18-k的奇偶性相同,且a+18+k≥18,于是 (a+18+k,a+18-k)=(112,2), 或 (a+18+k,a+18-k)=(56,4), 或 (a+18+k,a+18-k)=(28,8), 解得(a,k)=(39,55)或(a,k)=(12,26)或(a,k)=(0,10)(舍去). 因此,当a=39时,原方程的3个根为1,-1,-56;当a=12时,原方程的3个根为1,-2,-28. 3.2 四次不定方程 例10若关于x的方程x4-16x3+(81-2a)x2+(16a-142)x+a2-21a+68=0的各根为整数,求a的值并解此方程. (2009年江西省初中数学竞赛试题) 解原方程可化为 a2-(2x2-16x+21)a+ (x4-16x3+81x2-142x+168)=0, 于是 [a-(x2-6x+4)]·[a-(x2-10x+17)]=0, 则 x2-6x+4-a=0, 或 x2-10x+17-a=0. 可知Δ1=4a+20=4(a+5)和Δ2=4a+32=4(a+8)均为完全平方数.设a+5=m2,a+8=n2(m,n均为正整数),则 (m+n)(m-n)=-3, 易得m=1,n=2,此时a=-4,原方程的4个解为2,3,4,7. 评注本例通过“转换主元”利用因式分解,将一个四次方程转化为2个二次方程从而求解. 4.1 转化为整式不定方程 (2011年北京市初中数学竞赛试题) 解由题意,得xy-2 011x-2 011y-2 011=0,则 (x-2 011)(y-2 011)=2 011×2 012=22×503×2 011, 故原方程的正整数解有(2+1)(1+1)(1+1)=12组. 评注通过去分母,把分式方程转化为整式方程是解决分式方程问题的常用策略,不定方程亦如是. 4.2 利用整除求解 ( ) A.2 B.4 C.6 D.8 (2006年浙江省初中数学竞赛试题) 评注通过分式的变形,利用整除解决了本例中的分式不定方程,这比利用去分母转为整式方程解答更简洁. 4.3 利用“排序放缩” (2007年山西省太原市初中数学竞赛试题) 解由1≤x≤y≤z,得 若x=2,则 故 即 若x=3,则 故 则 综上可知,原方程的正整数解为 评注本例利用放缩确定每个未知数的范围,进而确定原方程的正整数解.另外,本题的题干部分已明确x≤y≤z,很多时候需依据题目中“轮换对称性”先“排序”后“放缩”. 5.1 借助“尾数分析” 例14设n是正整数,且n2+1 085是3的正整数次幂,则n的值为______. (2007年天津市初中数学竞赛试题) 解由n2(n为正整数)的个位数字只能是0,1,4,5,6,9,得n2+1 085的个位数字只能是5,6,9,0,1,4. 而3m(m为正整数)的个位数字只能是1,3,7,9.由已知可设n2+1 085=3m(n,m均为正整数),得3m的个位数字只能是1或9,故m是偶数.设m=2k(k为正整数),则n2+1 085=32k,于是 (3k-n)(3k+n)=1 085=1×5×7×31, 得 (3k-n,3k+n)=(1,1 085), 或 (3k-n,3k+n)=(5,217), 或 (3k-n,3k+n)=(7,155), 或 (3k-n,3k+n)=(31,35). 其中,只有(3k-n,3k+n)=(7,155)满足条件,此时k=4,n=74. 评注本例从完全平方数与3的正整数次幂的尾数分析入手,将不定方程变形后借助因式分解和分解质因数使问题得以解决,充分考虑了指数不定方程的“指数”特征,利用尾数的周期分布将原方程进行转化. 5.2 借助“奇偶分析” 例15能使2n+256是完全平方数的正整数n的值为______. (2011年全国初中数学联赛试题) 解当n<8时, 2n+256=2n(1+28-n), 若它是完全平方数,则n必为偶数.但易知1+28-n不是完全平方数. 当n>8时, 2n+256=28(2n-8+1). 若它是完全平方数,则2n-8+1为某个奇数的平方.设2n-8+1=(2k+1)2(k为自然数),则 2n-10=k(k+1), 由于k和k+1一个为奇数一个为偶数,则k=1,进而得到n=11. 评注指数不定方程的形式千姿百态,很多问题形式简单,解答较为复杂.不过由于初中所学内容的限制,命题时常常设定其解答方法为常用的相关策略,本例结合“2的正整数次幂”,借助“奇偶分析”加以解答. 不定方程作为数论的一个分支,有着悠久的历史与丰富的内容,其案例不一而足,对应的解法也不拘一格.很多不同形式的不定方程,其解法相通,往往需要多种方法同时运用,需要读者在深谙相关方法和技巧的基础上灵活运用.

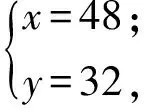
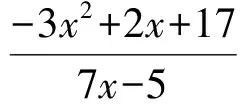
3 高次不定方程
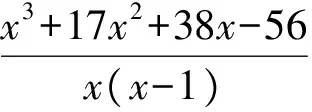
4 分式不定方程
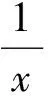
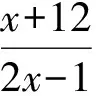

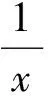
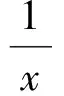

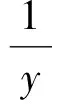
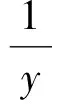
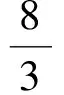

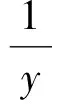
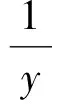
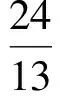
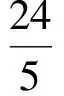
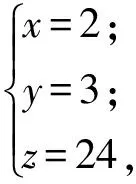
5 指数不定方程
