投资者情绪与股市波动分解＊

高大良，张小勇

（湖南大学 工 商管理学院，湖南 长 沙 410082）

一 引 言

在传统金融理论中，资产价格波动由基本经济因素决定，并不受投资者行为等因素的影响。但是，金融市场中存在着基本经济因素无法解释的过度波动现象，因此，大量的学者试图从行为金融理论出发对这一问题进行研究。

关于投资者情绪对资产价格波动的影响，最早的理论模型来自De Long等对噪声交易的经典研究［1］。在他们提出的噪声交易模型中，投资者情绪会成为影响资产价格的系统性风险，从而对资产价格波动产生影响。随后，大量学者通过构建投资者情绪指标对这一问题进行实证研究，已有的结论基本上都认为投资者情绪对股市波动具有一定的解释能力，并且高情绪会提高价格波动。例如，Brauer研究了噪声交易行为与基金收益波动之间的关系，发现前者能够解释大约7%的波动［2］。Brown将美国个体投资者协会指数作为投资者情绪的代理变量，发现投资者情绪的异常波动会导致封闭式基金收益的巨大波动［3］。许承明和宋海林（2005）采用封闭式基金折价率作为情绪指标，也得到了类似的结论［4］。杨阳和万迪则研究了不同市场态势下投资者情绪对波动的影响，结果发现牛熊市下投资者情绪对波动的影响存在异化现象［5］。林树和俞乔通过心理学实验研究发现，在资产价格顶部附近，情绪波动和资产价格主要由经济基本面的变化决定，两者相互作用并形成反馈环，最终可能形成市场泡沫并引起市场崩溃［6］。

以上研究大多着眼于投资者情绪对资产价格整体波动的影响，而没有对其影响机制进行深入分析。本文借助于Pollet和Wilson的波动分解理论，将市场整体波动分解为平均相关性和平均波动，进而构建投资者情绪指标来研究投资者情绪是如何影响市场波动的。文章接下来的安排如下：第二部分为投资者情绪的构建以及相关数据的预处理，第三部分为实证结果，第四部分结论。

二 投资者情绪与数据预处理

（一）投资者情绪

本文遵循Baker和Wurgler的经典方法来构建投资者情绪复合指标［8］，结合中国市场的实际情况，原始投资者情绪指标选为：封闭式基金折价率（CEFD）、IPO数量（NIPO）、IPO首日收益（RIPO）、换手率（TURN），样本为2000年1月至2011年12月的月度数据，一共144个样本，所有数据均来自锐思数据库。同时，参考宋泽芳和李元的研究［9］，本文选取消费物价指数（CPI）、生产者物价指数（PPI）、宏观经济预警指数（MI）这三个指标来对宏观经济变量加以控制，数据来自中国国家统计局。

根据Baker和Wurgler的方法，本文首先对四个原始情绪指标在即期数据和滞后一期数据中进行了选取，并进一步对各个原始指标进行了去除宏观经济因素的预处理，用得到残差序列作为新的原始情绪指标序列。这样，通过主成分分析得到了去除宏观经济因素的第一主成分如下：

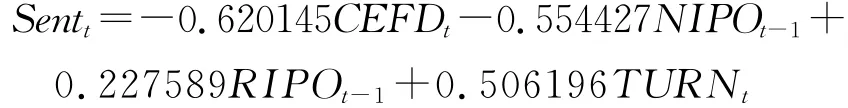
这里的第一主成分能够解释方差变异的46.06%。Baker和 Wurgler（2006）认为第一主成分能够很好的代表各个原始情绪指标的共同成分，可以作为投资者情绪的代理指标，因此，本文沿用这一经典方法，同样采用第一主成分作为投资者情绪的代理指标。

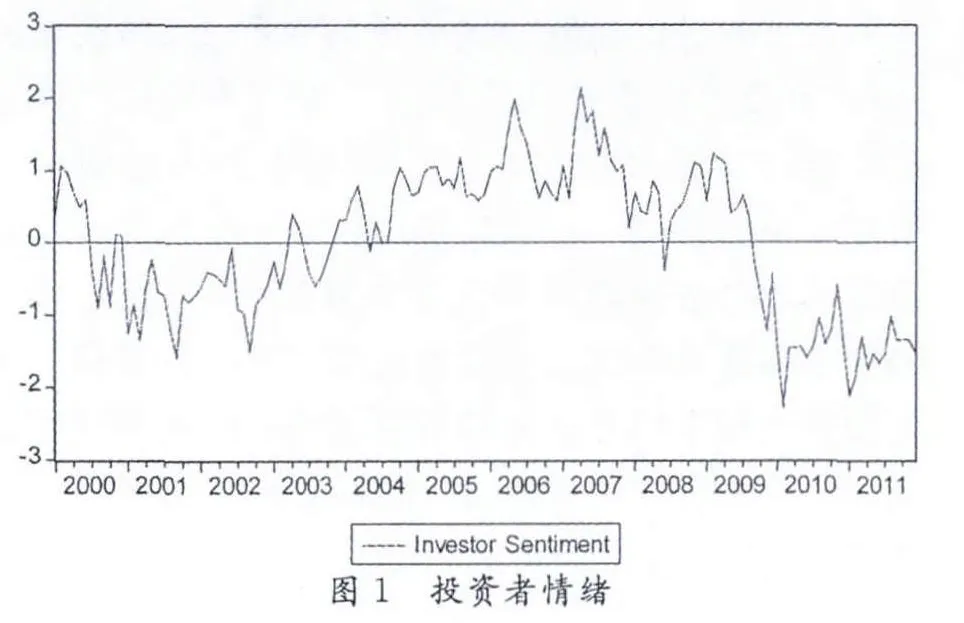
图1 投资者情绪

根据前面所得到的情绪指标，可以绘制出投资者情绪曲线，如图1所示。从图1可以看出，本文所构建的投资者情绪指标与我们对投资者情绪变化的直观感受是基本吻合的。总体来说，在2000年到2011年的这十几年间，中国股票市场上的投资者情绪经历了较大的波动过程，集中体现在2006年左右的股市情绪高涨，以及随之而来的全球金融危机所带来的持续情绪低迷。

（二）数据处理以及统计性描述

对应投资者情绪指标的样本期限，本文选取了2000年1月到2011年12月间的42只A股为样本，同时选取上证A股指数作为市场指数，月度平均相关性、月度平均方差以及月度股市方差均由日度数据计算得到，计算方法参考Pollet和Wilson的相关指标计算方法，通过加总日度数据得到月度数据。具体计算方式如下所示：

1.市场波动（Market Variance，MV）：

其中rt，d为t月的第d个交易日的股市超额收益，nt为t月内交易日的个数，20为平均月度交易日数量。

2.平均方差（Average Variance，AV）：

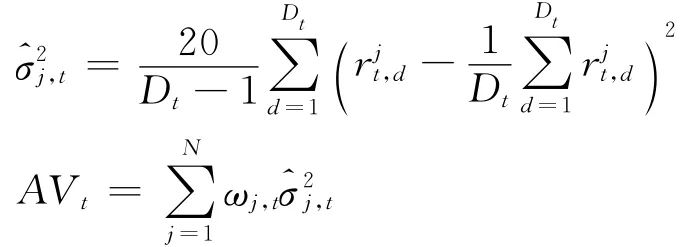
3.平均相关性（Average Correlation，AC）：

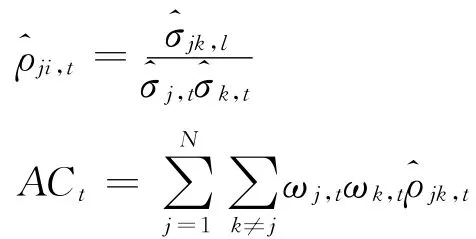
市场波动、平均相关性和平均方差的月度数据的描述性统计如表1所示：

从表1可以看出，个股的平均相关性达到了0.403531，这说明个股间的协同运动比较明显。个股的平均方差大约是市场方差的三倍，这说明由大量股票构成的投资组合确实能够分散风险。市场方差和平均方差的相关性较高，为0.851571，而平均相关性和平均方差之间的相关性程度较低，只有0.274765。

表1 各指标的描述性统计

本文还进一步分析了不同情绪状态下各个指标的描述性统计量，分析发现，所有指标描述性统计在不同的情绪期都有所不同。在高情绪期，无论是个股的平均方差还是市场方差，都要比低情绪期要大。而平均相关性则与此相反，在高情绪期平均相关性较低，在低情绪期平均相关性则较高。这说明高情绪虽然会通过加剧个股波动来提高市场总体波动，但是会同时降低个股之间的相关性，这样有利于风险的分散而最终削弱了高情绪对总体波动的影响。情绪对总体波动的这一影响机制将在随后的实证中进行进一步的分析。

三 实证结果

（一）股市波动分解

Pollet和Wilson将市场方差分解为平均相关性和平均波动的乘积［7］，该理论可以简单的用以下公式表示：其中为股市方差分别代表个股平均方差和个股平均相关性。

本节首先验证上述波动分解的有效性，对应于上述模型，验证市场波动分解有效性的计量模型设计为如下形式：

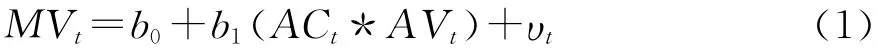
其中E［υt｜ACt＊AV］＝0。这里b0预期为0，而b1预期为1。市场波动分解的有效性可以通过模型的R2来衡量，R2越高，表明波动分解越有效。同时，参照Pollet和Wilson（2010）的做法，作为对比，本文还给出了其他分解方式的计量模型及其实证结果，具体方程不再列出。实证结果如表2所示：

表2 市场波动分解

表2中第1列即为模型（1）的估计结果，其R2为0.912247，且为四个模型中的最大值，这表明市场波动的绝大部分都能够被平均相关性和平均方差的乘积项所解释，并且其解释能力优于其他模型，这说明市场波动分解是有效的。b0和b1与预期的值存在一定的差异，其中b0虽然很小，但是显著为正，这表明市场波动中存在着平均相关性和平均方差所无法解释的系统性成分；b1并不等1则可能是由于相关指标的计算方法以及测量误差的存在而造成的。表2的第2列和第3列分别验证了平均相关性和平均方差对市场波动的单独解释能力，和预期的一样，其相关关系都是为正的。其中平均相关性能够解释市场波动的34.4826%，而平均方差则可以解释市场波动的72.5173%，这也从另一个角度说明了两者对市场方差都具有解释能力，并且平均方差和市场波动的相关性更为强烈。第4列显示了平均相关性和平均方差分别对市场波动的联合线性影响，其R2达到了0.860139，同样解释了市场波动的大部分。

（二）投资者情绪影响股市波动的具体机制

本小节在股市波动分解的基础上对投资者情绪影响股市波动的具体机制进行深入研究。首先，和以往的研究类似，本文先考察投资者情绪对股市整体波动的影响，如公式（2）所示。然后考察投资者情绪对股市波动分解后的两个成分的影响，即投资者情绪对平均相关性和平均波动的影响，如公式（3）（4）所示。

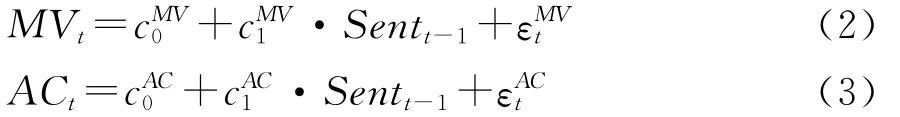
模型（2）即投资者情绪影响股市波动的总体效应，由于股市波动可以分解为平均相关性和平均方差的乘积，因此，模型（3）（4）可以看做是投资者情绪对股市波动影响的分解效应。由于股市波动可以分解为平均相关性和平均方差的乘积，这样，模型（2）（3）（4）与模型（1）构成了投资者情绪对股市波动的影响机制模型。

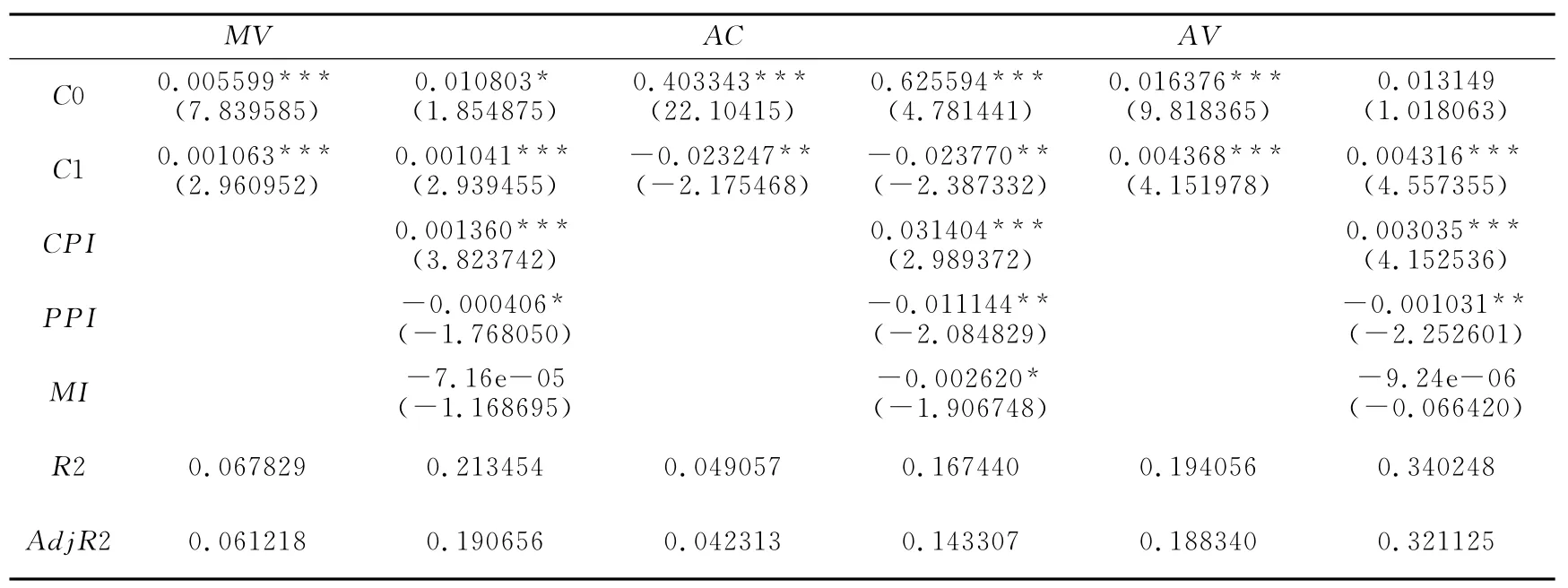
表3 投资者情绪影响股市波动的具体机制

表3给出了上述模型的实证结果。先看总体效应，投资者情绪和股市波动存在着显著的正相关关系，当投资者情绪高涨时，股市波动会增加，而当投资者情绪低落时，股市波动也会相应降低。再看分解效应，投资者情绪和平均相关性存在着显著的负相关关系，即当投资者情绪高涨时，单个股票之间的价格变化趋势会被削弱，这也和以往的研究结论是一致的。投资者情绪和平均波动之间存在着显著的正相关关系，而且投资者情绪对平均波动的影响程度要比对股市波动的影响程度要大。结合3.1节的结论：股市波动可以分解为平均相关性和平均波动两项的乘积，我们可以这样认为，投资者情绪对股市波动的影响是通过影响平均相关性和平均波动来实现的，投资者情绪对股市波动和平均波动都具有正向的影响，但是投资者情绪对个股波动的影响要更大，由于投资者情绪的高涨同时降低了个股之间的平均相关性，这也将削弱股市波动的总体效应。

（三）投资者情绪与市场波动分解

投资者情绪会影响市场波动，并且这种影响是通过影响平均相关性和平均方差来实现的，那么，投资者情绪是否会影响股市波动分解呢？为了进一步验证投资者情绪的这种可能影响，本文还设置了如下的两区制计量模型：

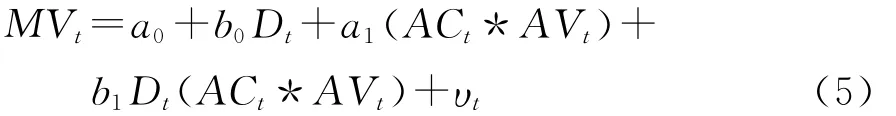
这里，Dt为投资者情绪的虚拟变量，等于1时代表高情绪期，等于0时代表低情绪期。同样，对应于表2中的所有市场波动分解方式，设置了相应的两区制方程，具体方程不再列出。实证结果如表4所示。

表4的结果显示了投资者情绪对市场波动分解的影响。从模型（5）的结果来看（即表4中第1列），投资者情绪并不影响平均相关性和平均方差的乘积项和市场波动之间的关系，也就是说，无论在高情绪期还是在低情绪期，市场波动分解的结构都是不变的。在第2列至第4列可以看到，当市场波动分解方程设置为关于平均相关性和平均方差的线性表示时，投资者情绪仍然可能产生重要的影响。其中，第4列的结果尤为重要，从这里可以看出，在不同的情绪期，平均相关性和平均方差对市场波动的解释能力是不同的。具体而言，在高情绪期，平均相关性对市场波动的影响更大，而平均方差的影响则变小。投资者情绪对两者的这种反向影响，可能是它们的乘积项对投资者情绪并不敏感的原因。

表4 投资者情绪与市场波动分解

四 结 论

本文进一步研究了投资者情绪影响股市波动的具体机制问题。首先采用Pollet和Wilson的股市波动分解方法，将股市总体波动分解为平均相关性和平均方差的乘积，随后借鉴Baker和Wurgler的经典方法构建了投资者情绪，并设计了实证方法来研究投资者情绪是如何具体影响股市总体波动的内在结构的。本文的主要结论有：

1.股市总体波动可以分解为平均相关性和平均方差的乘积，并且这种分解方法是有效的。这说明股市总体波动特征不仅取决于个股的波动大小，也取决于个股之间的相关性大小。

2.投资者情绪会影响股市总体波动，并且这种影响具体是通过影响个股波动和个股之间的相关性来实现的。总的来说，高涨的情绪会加剧市场总体波动，这与以往的结论是一致的。进一步的，高情绪对股市总体波动的这种影响主要是通过加剧个股波动来实现的，但另一方面，高涨的情绪也会降低个股之间的相关性，从而对投资者情绪加剧股市总体波动的过程起到一定的反向修正作用。

3.投资者情绪并不会影响股市总体波动的分解，这也从侧面印证了投资者情绪对平均相关性和平均方差的影响是反向的。

［1］ De Long B J，Shleifer A，Summers H L，et al.Noise Trader Risk in Financial Markets［J］.Journal of Political Economy，1990，98（4）：703－738.

［2］ Brauer G A.“Investor sentiment”and the closed－end fund puzzle：A 7percent solution［J］.Journal of Financial Services Research，1993，7（3）：199－216.

［3］ Brown G W.Volatility，sentiment，and noise traders［J］.Financial Analysts Journal，1999，55（2）：82－90.

［4］ 许承明，宋海林.中国封闭式基金价格报酬过度波动的经验分析［J］.经济研究，2005（3）：108－118.

［5］ 杨阳，万迪.不同市态下投资者情绪与股市收益、收益波动的异化现象——基于上证股市的实证分析［J］.系统工程，2010（1）：19－23.

［6］ 林树，俞乔.有限理性、动物精神及市场崩溃：对情绪波动与交易行为的实验研究［J］.经济研究，2010（8）：115－127.

［7］ Pollet J M，Wilson M.Average correlation and stock market returns［J］.Journal of Financial Economics，2010，96（3）：364－380.

［8］ Baker M，Wurgler J.Investor Sentiment and the cross－section of stock Returns［J］.Journal of Finance，2006，61（4）：1645－1680.

［9］ 宋泽芳，李元.投资者情绪与股票特征关系［J］.系统工程理论与实践，2012，32（1）：27－33.