基于ITD和模糊聚类的齿轮箱故障诊断方法
2013-10-24段礼祥张来斌岳晶晶
段礼祥,张来斌,岳晶晶
(中国石油大学机械与储运工程学院,北京 102249)
对齿轮箱进行故障诊断,能够减少齿轮箱故障带来的经济损失,提高齿轮箱运行的可靠性和安全性。针对齿轮箱振动信号所具有的强烈的非平稳特性,信号处理方法主要有小波变换[1]、Wigner-Ville分布[2]、EMD 分解[3]。然而,小波变换是对时频平面的一种机械格型分解,缺乏对所研究信号的自适应性[4];Wigner-Ville分布作为时频分析方法,可同时从时域和频域对时间序列进行分析,但分析多分量信号时易产生交叉项[5];EMD分解具有很强的自适应性,能够有效地分析非线性与非平稳信号,但存在端点效应、模态混叠,筛选过程和计算复杂度高,不利于实时计算[6]等缺陷。而Mark G.F.和Osorio I.[7]提出的固有时间尺度分解(intrinsic time-scale decomposition,ITD)是一种新的非平稳信号时频分析方法。该方法能够精确地提取信号的瞬时特征,有较高的拆解效率和频率分辨率,可以实时处理大量数据[8-9]。因此,笔者将 ITD和模糊聚类(FCM)相结合应用到齿轮箱的故障诊断中以期取得更高的准确性与效率。
1 固有时间尺度分解算法
ITD算法是将待分解的非平稳信号分解成一系列的固有旋转分量与一个单调的趋势分量之和,分解得到的每层固有旋转分量定义了瞬时频率、瞬时幅度等时频信息[10]。对于待分解的信号Xt,定义一个基线提取算子L,使得从信号Xt中抽取一个基线后剩下的余量信号成为一个固有旋转分量(proper rotation component,PRC)。信号Xt的一次分解的表达式为
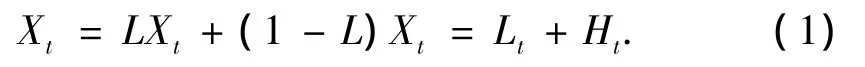
式中,Lt和Ht分别为一次分解后得到的基线信号和固有旋转分量。
假设{τk,k=1,2,…}是信号 Xt的局部极值所对应的时刻,定义τ0=0。为简化符号,分别用Xk、Lk表示 X(τk)、L(τk)。假设 Lt和 Ht在[0,τk]上有定义,Xt在[0,τk+2]有定义,在区间(τk,τk+1]上的连续极值点之间定义一个分段线性基线提取因子L:
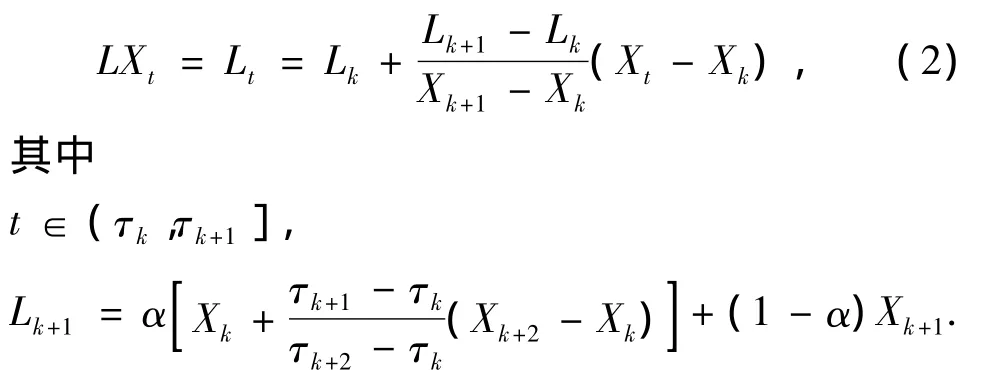
α是固有旋转分量幅度按线性比例提取的增益控制参数,α ∈ (0,1),通常取0.5。
由式(2)定义了基线信号之后,定义一个固有旋转分量提取算子H:
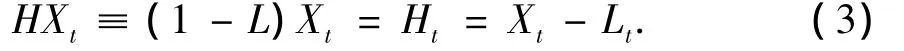
一次分解后得到一个基线信号Lt和一个固有旋转分量Ht,后者表示信号中的局部相对高频成分。将基线信号Lt作为输入信号继续进行分解,直到获得的基线信号变得单调或者小于某个预定值为止。这就将原信号分解成若干个从高到低不同频率段的固有旋转分量之和与一个单调趋势分量。信号Xt的整个分解过程可表示为
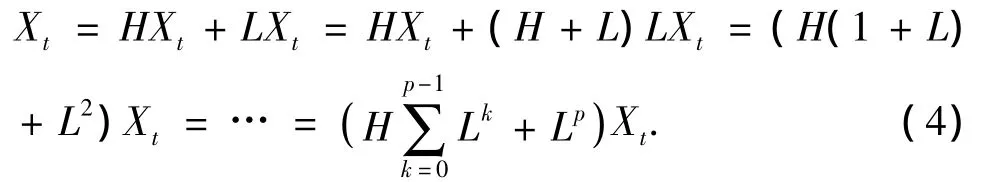
ITD方法提出了一种新的瞬时频率计算方法,避免了Hilbert变换在计算瞬时频率时存在的边缘效应和偶尔出现负频率的问题[7]。对每一层分解得到的固有旋转分量进行单波分析,可以快速计算信号局部的瞬时幅值、相位和频率。
瞬时幅值可表示为
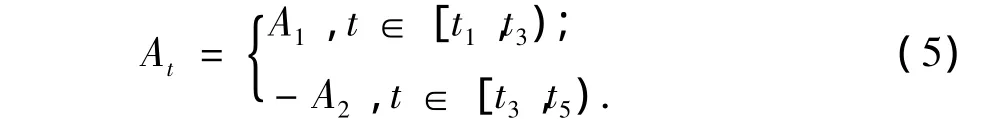
式中,A1和A2(A1>0,A2>0)分别为一个单波内两个上过零点t1和t5时刻之间正、负半波的极点幅度;t3为下过零点时刻。
瞬时相位的计算公式为
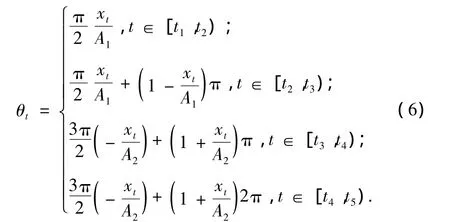
式中,xt为ITD分解后的固有旋转分量;t2和t4分别为正、负半波的极点时刻。
根据瞬时相位,对其微分得到瞬时频率:

2 模糊C-均值聚类算法
将有限样本集X={x1,x2,…,xn}划分成c类(2<c<n),用uij表示第j个样本对第i类的隶属度。分类结果用模糊矩阵Uc×n表示,其元素uij具有如下性质:
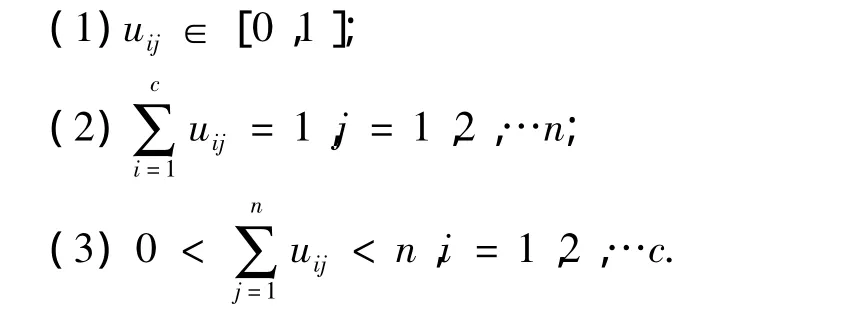
定义一个目标函数Jm(U,V),Jm(U,V)表示各类样本到聚类中心的加权距离平方和[11]:
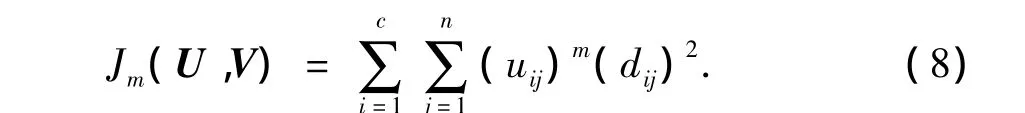
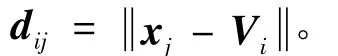
FCM算法的实质就是寻找一组中心矢量,使得目标函数Jm(U,V)达到最小值。通过对目标函数的优化,找到uij和dij之间的关系,通过Lagrange乘子法使Jm(U,V)取极小值的必要条件为
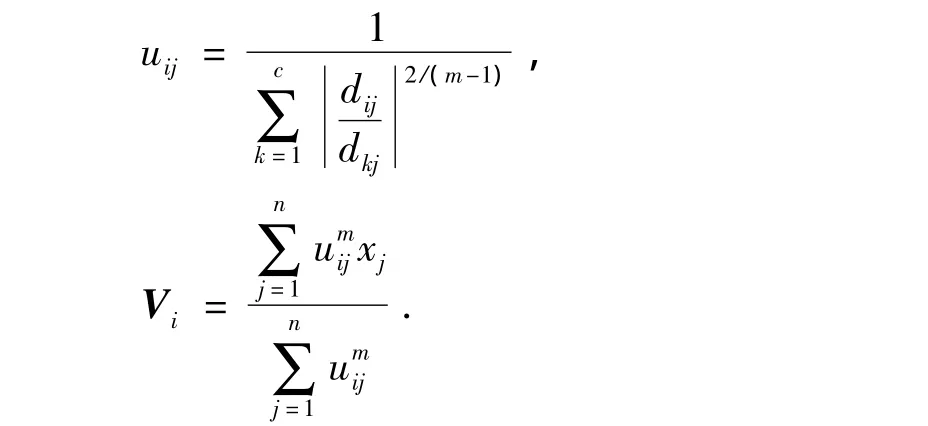
若样本集X、聚类数c和加权指数m已知,就能通过迭代算法确定最佳模糊分类矩阵U和聚类中心V。
3 工程应用
3.1 基于ITD的齿轮箱故障特征提取
以新疆塔里木油田某作业区3#、5#往复式注水泵一级减速齿轮箱为对象,齿轮箱型号均为TD-8060,输入轴转速为1439 r/min,大齿轮齿数Z2=163,小齿轮齿数Z1=20。转轴频率fr=1439/60≈24 Hz,啮合频率fz=24×20≈480 Hz。采样频率为4 kHz,振动测点位于输入轴轴承座垂直方向。选取这两台齿轮箱在不同时期分别处于正常、齿面磨损和齿根裂纹3种故障状态下的振动数据作为样本,每组故障状态有7组样本,前5组作为训练样本,后2组作为测试样本,即在3种故障状态的21组振动数据中前15组是训练样本,后6组是测试样本。每组数据由5 120个采样点组成。
已知3#齿轮箱的第10个样本属于齿面磨损,对其分别进行ITD和EMD分解,结果如图1所示((a)中编号从上到下依次为 PRC1、PRC2、PRC3、PRC4、PRC5、PRC6、PRC7、PRC8 和 r8,(b)中编号从上到下 依 次 为 imf1、imf2、imf3、imf4、imf5、imf6、imf7、imf8、imf9、imf10 和 r10)。ITD 分解耗时 0.078 s,EMD分解耗时0.436 s,可见ITD算法在计算速度上优于EMD算法。这是因为ITD算法不用样条插值,每分解一次就获得一个固有旋转分量,每次分解只须迭代一次,而EMD算法每获得一个IMF分量需要经过多次迭代。由图1可以看出,同EMD分解相比,ITD分解层数少,能够快速地得到单调趋势项从而停止分解。虽然ITD分解和EMD分解都存在端点效应,但是ITD方法产生的端点效应较小,并且端点效应被限制在端点处,不会向内传播从而影响整个数据序列。
ITD算法自适应地将齿轮箱振动信号分解成一系列具有不同时间尺度的固有旋转分量和一个单调趋势项,这些固有旋转分量的频率段从高到低依次排列,处于高频部分的固有旋转分量包含了故障的主要信息。分别对3#、5#齿轮箱在3种状态下的21组数据进行固有时间尺度分解,选取包含主要故障信息的前4个固有旋转分量PRC,计算各个PRC能量Ei以及总能量E,得到PRC特征能量Ei/E,进而构造故障特征向量 T =[E1/E,E2/E,E3/E,E4/E]。表1、2分别为3#、5#齿轮箱的21组数据样本所对应的故障特征向量。
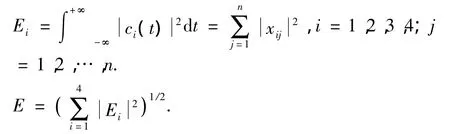
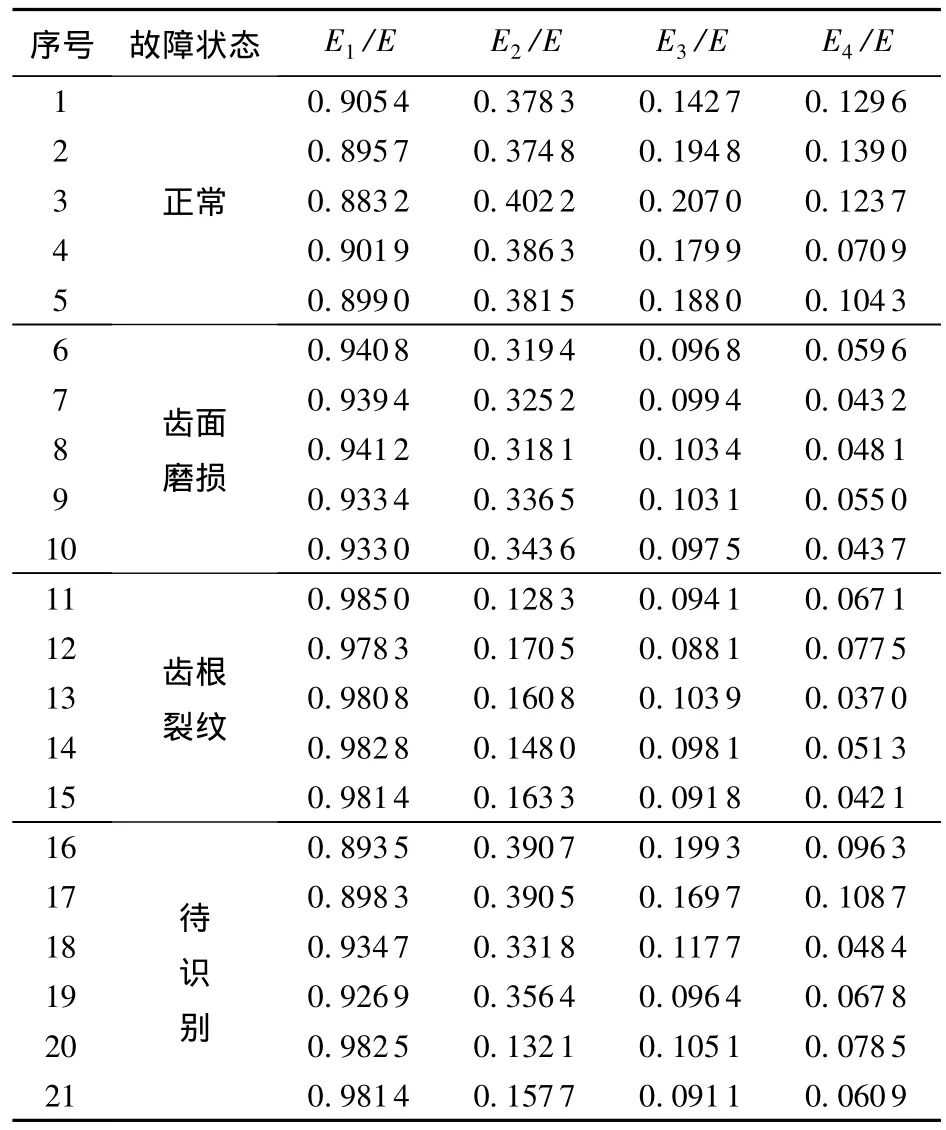
表1 3#齿轮箱的21组数据样本所对应的故障特征向量Table 1 Fault feature vectors of 21 samples of 3#gearbox
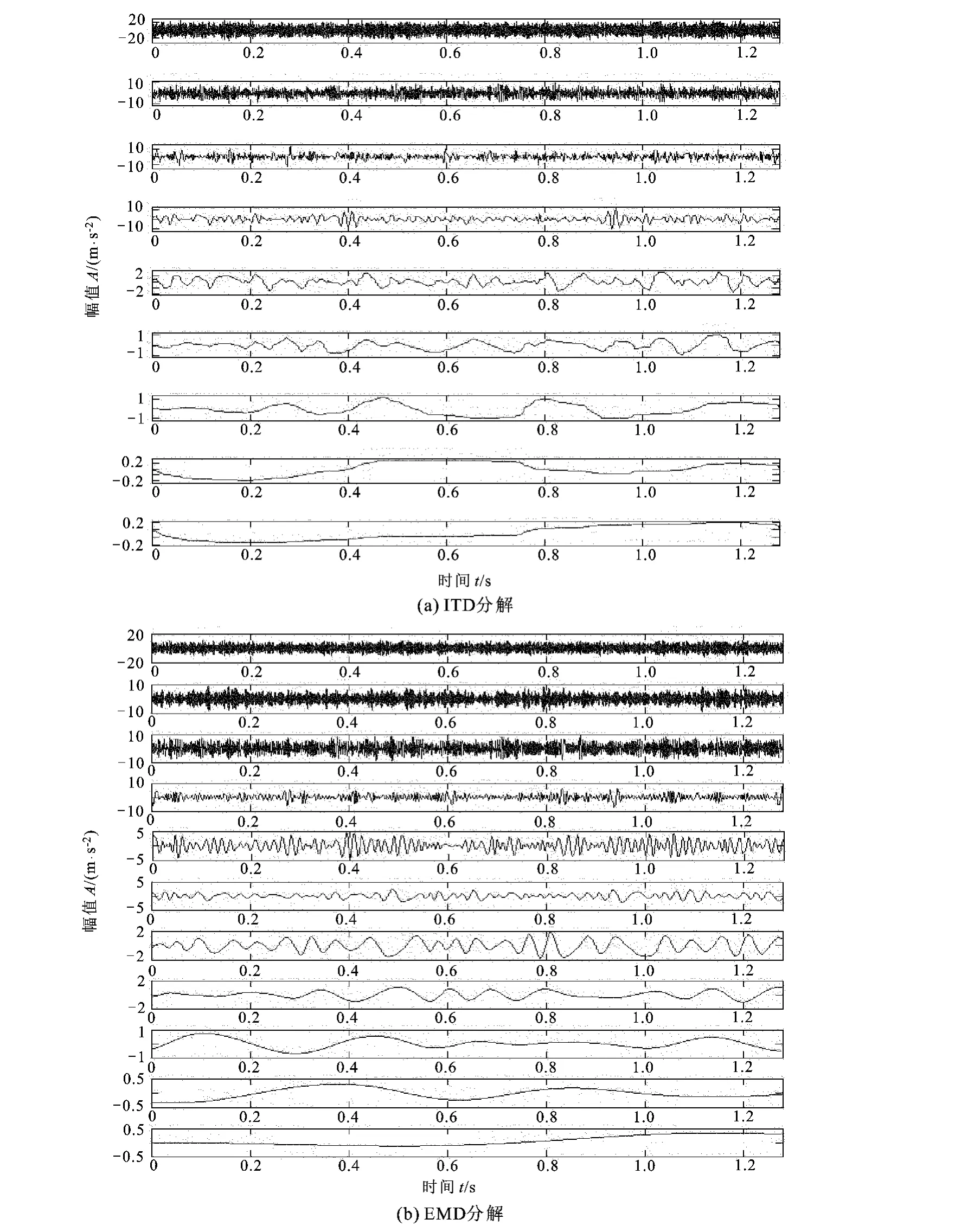
图1 3#齿轮箱的第10个样本的ITD、EMD分解结果Fig.1 Decomposition results of the 10th sample using ITD and EMD
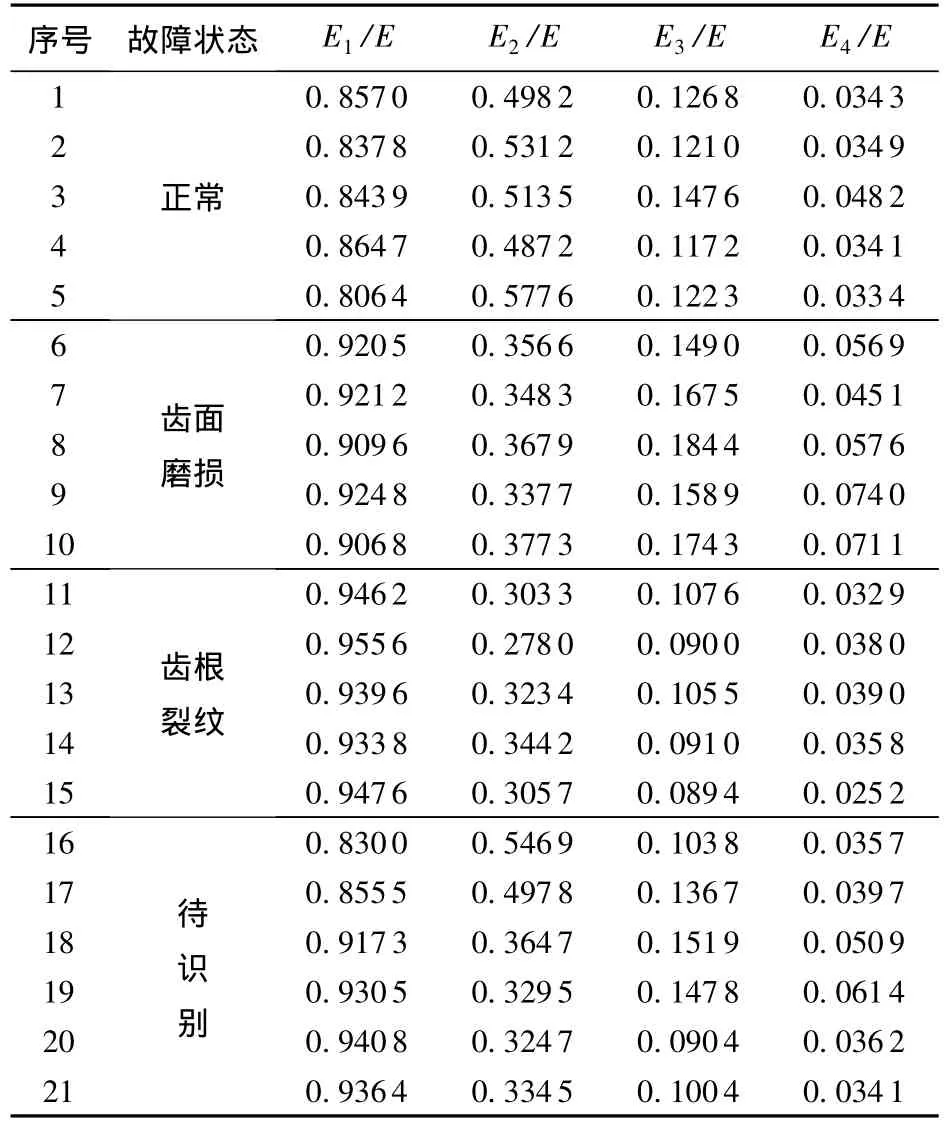
表2 5#齿轮箱的21组数据样本所对应的故障特征向量Table 2 Fault feature vectors of 21 samples of 5#gearbox
3.2 基于FCM的齿轮箱故障状态识别
表1中前15组数据为3#齿轮箱的已知故障样本,将其作为建立3#齿轮箱聚类标准的训练样本。确定样本的最佳分类数c=3,用A、B、C表示。FCM聚类中,模糊加权指数m的范围为1.5~2.5,一般选取中间值2[12]。通过对3#齿轮箱的15组训练样本进行模糊C-均值聚类,得到分类矩阵U3和聚类中心V3。分类矩阵U3如表3所示,其中的数值表示聚类后各样本对各个类别的隶属度。
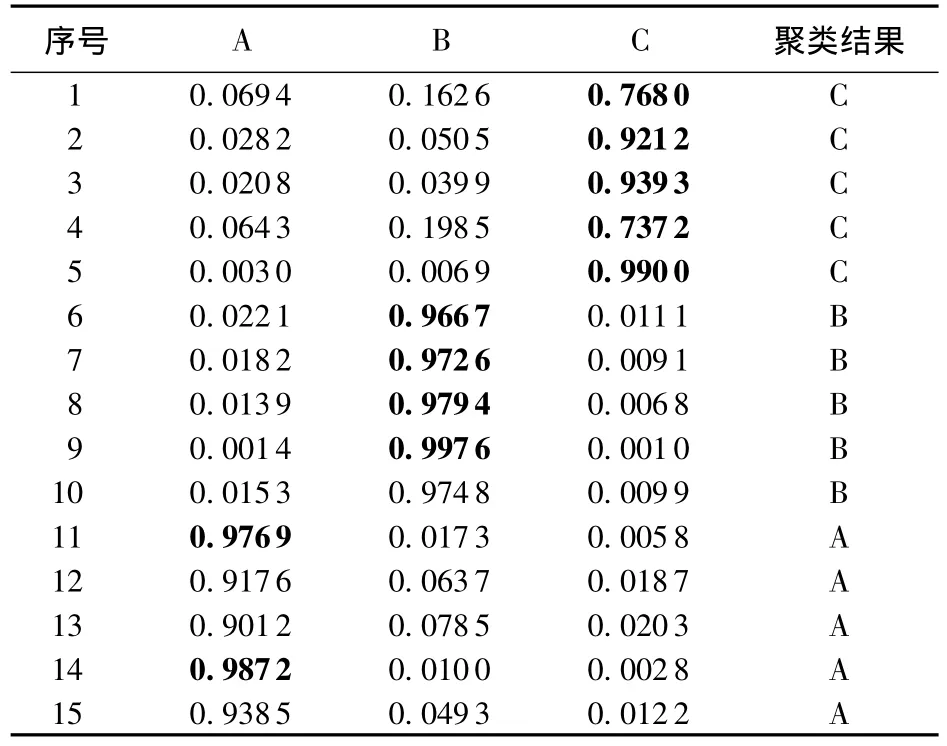
表3 3#齿轮箱的15个训练样本的分类矩阵以及聚类结果(ITD+FCM)Table 3 Classification matrix and clustering results of 15 training samples of 3#gearbox(ITD+FCM)
按照隶属度最大原则,表1中样本1~5属于C类,样本6~10属于B类,样本11~15属于A类。因此得到A类代表齿根裂纹,B类代表齿面磨损,C类代表正常状态。聚类中心V3的第1、2、3行分别是A、B、C类的聚类中心,分别对应齿根裂纹、齿面磨损和正常状态。将表1中的后6组待识别样本与聚类中心V3进行再聚类,其模糊隶属度和识别结果如表4所示。
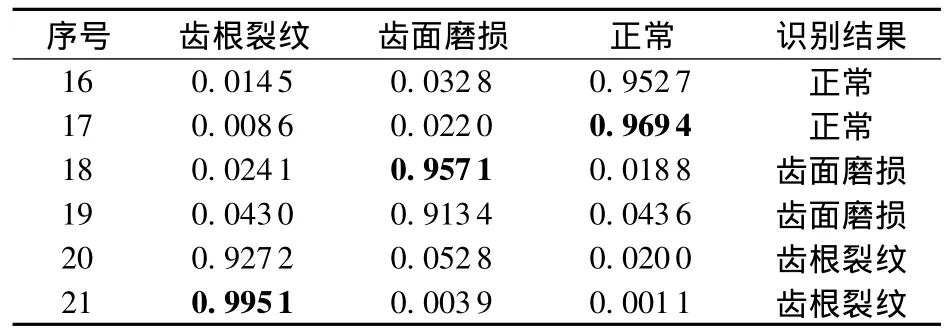
表4 3#齿轮箱的6个测试样本的识别结果(ITD+FCM)Table 4 Identification results of 6 test samples of 3#gearbox(ITD+FCM)
同理,对5#齿轮箱的15组训练样本进行模糊C-均值聚类,得到分类矩阵U5(表5)和聚类中心V5。按照隶属度最大原则,表2中样本1~5属于Ⅲ类,样本6~10属于Ⅱ类,样本11~15属于Ⅰ类。因此,Ⅰ类代表齿根裂纹,Ⅱ类代表齿面磨损,Ⅲ类代表正常状态。将表2中的后6组待识别样本与聚类中心V5进行再聚类,其模糊隶属度与识别结果见表6。
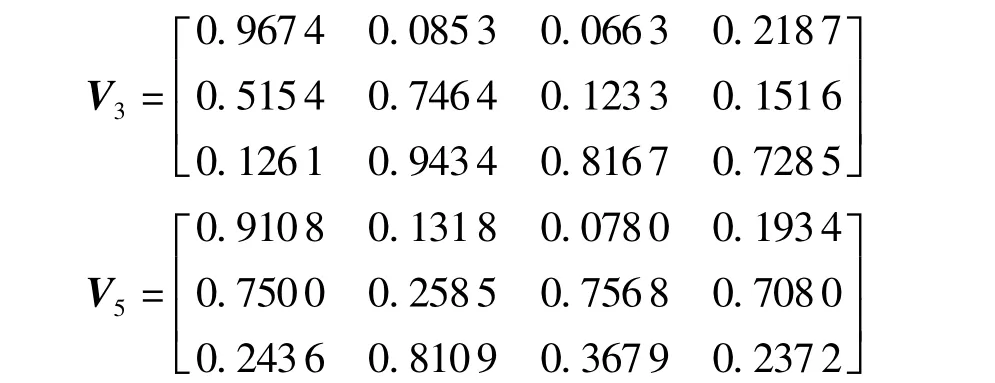
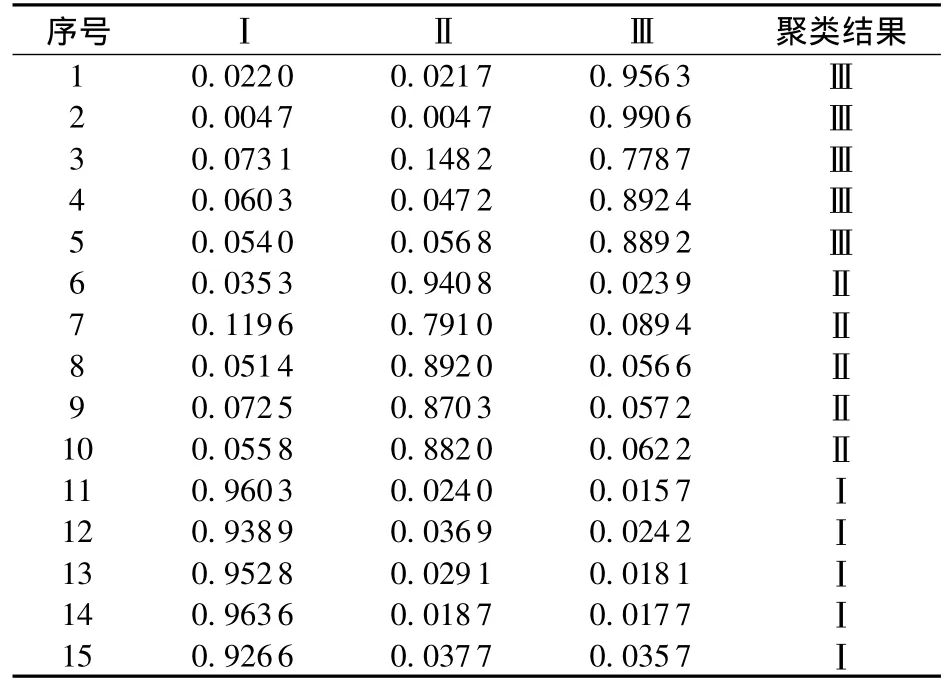
表5 5#齿轮箱的15个训练样本的分类矩阵以及聚类结果(ITD+FCM)Table 5 Classification matrix and clustering results of 15 training samples of 5#gearbox(ITD+FCM)
由表3和表4、表5和表6可得,3#和5#齿轮箱的所有样本的识别结果与实际情况全部相符,表明基于ITD和FCM的方法对齿轮箱故障诊断是有效的。
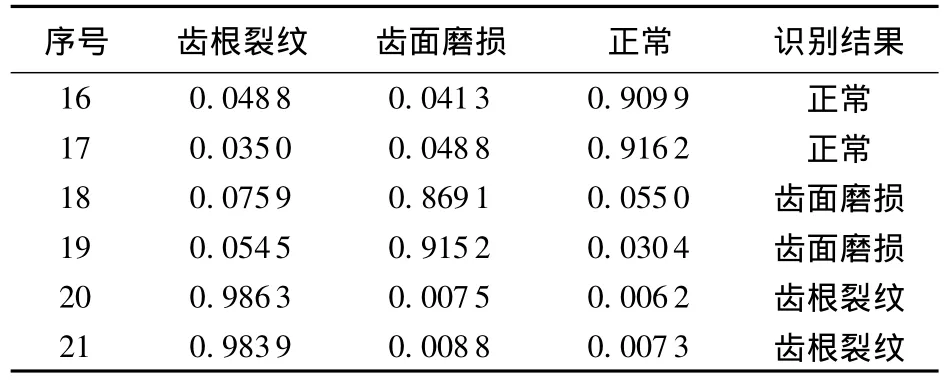
表6 5#齿轮箱的6个测试样本的识别结果(ITD+FCM)Table 6 Identification results of 6 test samples of 5#gearbox(ITD+FCM)
3.3 ITD+FCM与EMD+FCM对比
以3#齿轮箱为例,对其在正常、齿面磨损和齿根裂纹3种故障状态下的21组原始振动数据,分别进行EMD分解,提取前4个IMF分量,计算各个IMF能量E'i以及总能量E',构造故障特征向量T'=[E'1/E',E'2/E',E'3/E',E'4/E']。同样以前15组故障特征向量作为训练样本,采用FCM方法进行聚类分析,得到分类矩阵U'和聚类中心V'。

表7为15个训练样本的分类矩阵以及聚类结果,表8为6组待识别样本相对于各类聚类中心的模糊隶属度和最终的识别结果。
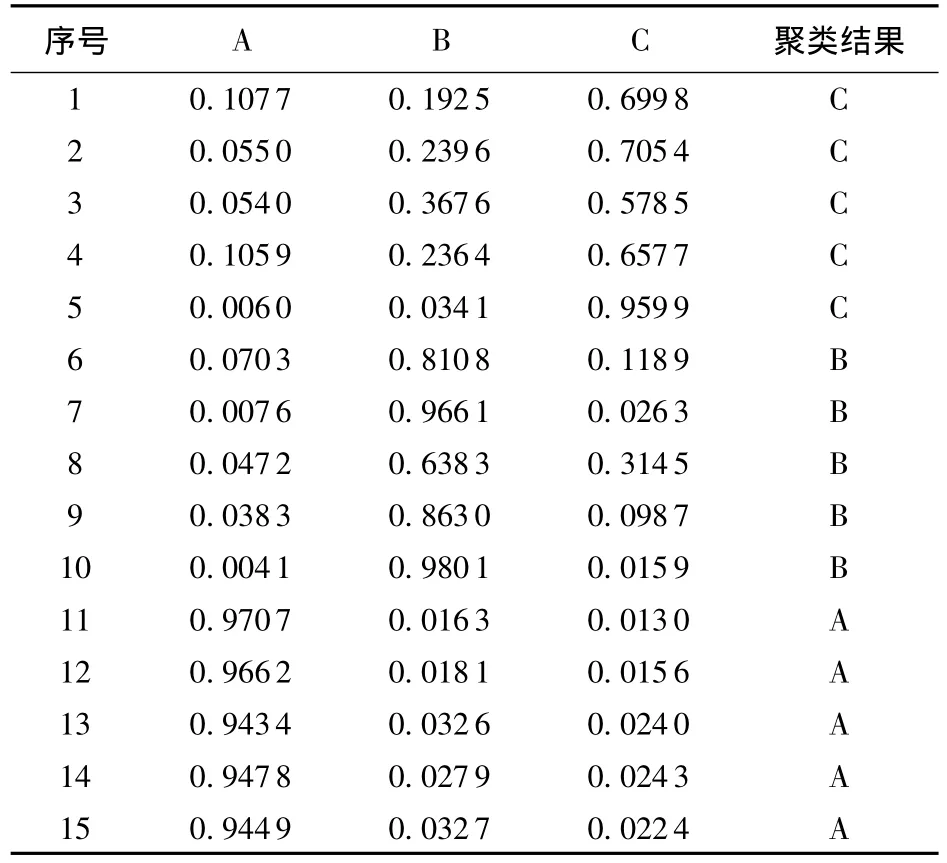
表7 3#齿轮箱的15个训练样本的分类矩阵以及聚类结果(EMD+FCM)Table 7 Classification matrix and clustering results of 15 training samples of 3#gearbox(EMD+FCM)
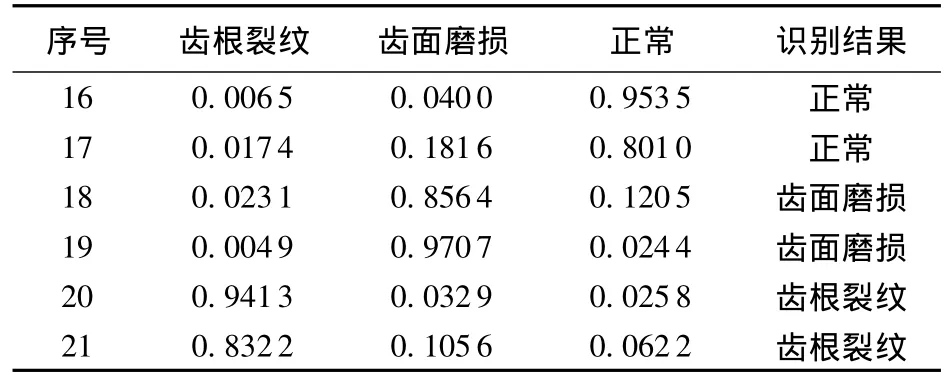
表8 3#齿轮箱的6个测试样本的识别结果(EMD+FCM)Table 8 Identification results of 6 test samples of 3#gearbox(EMD+FCM)
对比表3和表7、表4和表8,可知两种方法的聚类结果都正确,但采用ITD+FCM方法计算得到的各个样本的模糊隶属度的精度总体上高于EMD+FCM方法的,如表3、4中加粗字体所示。另外,ITD+FCM方法总共耗时1.45 s,EMD+FCM方法总共耗时10.467 s。因此,在计算速度和模糊隶属度的计算精度方面,ITD+FCM方法要优于EMD+FCM方法;ITD算法比EMD算法更适合用于齿轮箱故障特征的提取。
4 结束语
对现场采集的正常状态、齿面磨损和齿根裂纹3种状态下的齿轮箱振动信号进行固有时间尺度分解(ITD)和模糊C-均值聚类分析,实现了对齿轮箱故障的准确诊断。ITD算法适合分析非线性、非平稳信号,能自适应地将任意复杂信号分解成若干频率依次降低的固有旋转分量和一个单调趋势项。ITD算法不仅能够克服EMD算法的端点效应的缺陷,而且能够准确地提取出故障特征,计算速度快。模糊C-均值聚类算法的聚类效果好,分类效率高。将ITD与FCM相结合,为齿轮箱故障诊断提供了一种新的有效方法。
[1] SARAVANAN N,RAMACHANDRAN K I.Incipient gear box faultdiagnosisusing discrete wavelettransform(DWT)for feature extraction and classification using artificial neural network(ANN)[J].Expert Systems with Applications,2010,37(6):4168-4181.
[2] 沈国际,陶利民,温熙森,等.基于Wigner分布的齿轮箱振动信号相位估计[J].机械工程学报,2004,40(9):185-189.SHEN Guo-ji,TAO Li-min,WEN Xi-sen,et al.Phase estimation of gearbox vibration signal based on Wigner distribution[J].Chinese Journal of Mechanical Engineering,2004,40(9):185-189.
[3] GAI G H.The processing of rotor startup signals based on empirical mode decomposition[J].Mechanical Systems and Signal Processing,2006,20(1):222-235.
[4] 林近山.基于本征时间尺度分解算法的齿轮箱故障诊断[J].机械传动,2011,35(9):51-53.LIN Jin-shan.Fault diagnosis of gear box based on intrinsic time-scale decomposition algorithm [J].Journal of Mechanical Transmission,2011,35(9):51-53.
[5] 郭艳平,颜文俊.基于EMD和优化 K-均值聚类算法诊断滚动轴承故障[J].计算机应用研究,2012,29(7):2555-2557.GUO Yan-ping,YAN Wen-jun.Fault diagnosis of bearing based on empirical mode decomposition and K-means clustering [J].Application Research of Computers,2012,29(7):2555-2557.
[6] 安金坤,田斌,易克初,等.基于ITD的跳频信号跳速估计算法[J].系统工程与电子技术,2011,33(1):166-169.AN Jin-kun,TIAN Bin,YI Ke-chu,et al.Intrinsic timescale decomposition based algorithm for the hop rate estimation of frequency hopping signal[J].Systems Engineering and Electronics,2011,33(1):166-169.
[7] MARK G F,OSORIO I.Intrinsic time-scale decomposition:time-frequency-energy analysis and real-time filtering of non-stationary signals[J].Proc R Soc A,2007,463:321-342.
[8] 安学利,蒋东翔,陈杰,等.基于ITD和LS-SVM的风力发电机组轴承故障诊断[J].电力自动化设备,2011,31(9):10-13.AN Xue-li,JIANG Dong-xiang,CHEN Jie,et al.Bearing fault diagnosis based on ITD and LS-SVM for wind turbine[J].Electric Power Automation Equipment,2011,31(9):10-13.
[9] AN Xue-li,JIANG Dong-xiang,CHEN Jie,et al.Application of the intrinsic time-scale decomposition method to fault diagnosis of wind turbine bearing[J].Journal of Vibration and Control,2012,18(2):240-245.
[10] 安金坤,田斌,孙永军,等.一种基于ITD算法的直扩信号检测算法[J].电子与信息学报,2010,32(5):1178-1182.AN Jin-kun,TIAN Bin,SUN Yong-jun,et al.An algorithm for direct sequence spread spectrum signal detection based on intrinsic time-scale decomposition[J].Journal of Electronics& Information Technology,2010,32(5):1178-1182.
[11] 印兴耀,叶端南,张广智.基于核空间的模糊聚类方法在储层预测中的应用[J].中国石油大学学报:自然科学版,2010,36(1):53-59.YIN Xing-yao,YE Duan-nan,ZHANG Guang-zhi.Application of kernel fuzzy C-means method to reservoir prediction[J].Journal of China University of Petroleum(Edition of Natural Science),2010,36(1):53-59.
[12] 王朝晖,姚德群,段礼祥.基于模糊聚类的油田往复压缩机气阀故障诊断研究[J].机械强度,2007,29(3):521-524.WANG Zhao-hui,YAO De-qun,DUAN Li-xiang.Study on the method of oil field reciprocating compressor valve fault diagnosis based on fuzzy clustering[J].Journal of Mechanical Strength,2007,29(3):521-524.
