混合序列的一个强大数律
2013-10-24沈建伟
沈建伟
(浙江科技学院 理学院,杭州 310023)
沈建伟
(浙江科技学院 理学院,杭州 310023)
1 引言及引理

ρ(,
对k≥0,令
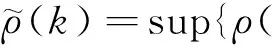
(1)

定义1对随机序列{Xn,n≥1},若ρ(k)→0,k→∞,则称{Xn,n≥1}为ρ混合序列。
定义2对随机序列{Xn,n≥1},若存在k∈,使得则称{Xn,n≥1}为混合序列。
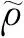
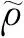
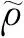
(2)
(3)
(4)
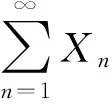
2 主要结果
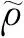
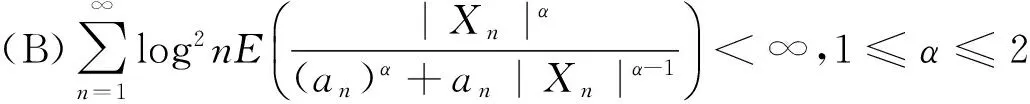
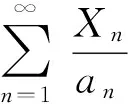
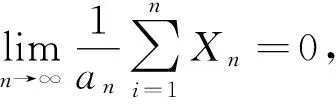
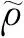
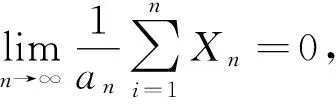
3 定理的证明

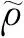
当α>0,|Xn|≥an>0时,有
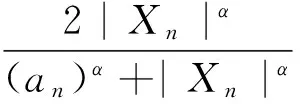
(5)
从而
由条件(A)可得
(6)
当α≥1,|Xn|≥an>0时,有
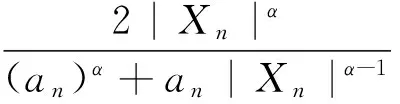
(7)
由条件(B)可得
(8)
由式(6)和式(8)可知引理1中的条件(2)成立。
当0<α≤1时,
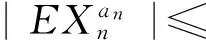
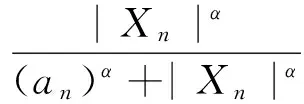
(9)
当α≥1时,由EXn=0和式(7)得
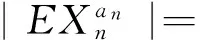
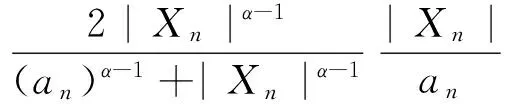
(10)
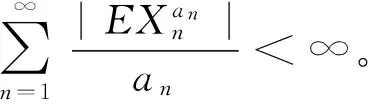
于是引理1中的条件(3)成立。
最后,
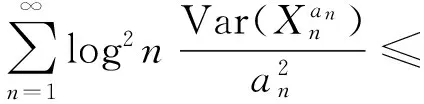
(11)
当0<α≤1时,由式(11)可知:
(12)
当1≤α≤2时,由式(11)可知:
(13)
由式(12)和式(13)可知:引理1的条件(4)成立。
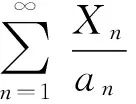
推论1的证明由定理1可知结论是显然的。
[1] Kolmogorov A N, Rozanov Y A. On strong mixing conditions for stationary Gaussian process[J]. Theory of Probability & Its Applications,1960,5(2):204-208.
[2] Bradley R C. Equivalent mixing conditions for random fields[J]. The Annals of Probability,1993,21(4):1921-1926.
[3] Bradley R C. On the spectral density and asymptotic normality of weakly dependent random fields[J]. Journal of Theoretical Probability, 1992,5(2):355-373.
[4] 吴群英.ρ混合序列的若干收敛性质[J].工程数学学报,2001,18(3):58-64,50.
[5] 吴群英.ρ混合序列加权和的完全收敛性和强收敛性[J].应用数学,2002,15(1):1-4.
[10] Guo M L, Dong J, Ren Y. Complete moment convergence of weighted sums for arrays of rowwiseρ*-mixing random variables[J].应用数学,2013, 26(1): 18-27.
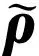
SHEN Jianwei
(School of Sciences, Zhejiang University of Science and Technology, Hangzhou 310023, China)
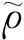
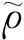
10.3969/j.issn.1671-8798.2013.05.001
2013-05-03
沈建伟(1972— ),男,浙江省萧山人,讲师,硕士,主要从事概率极限理论研究。
O211.4
A
1671-8798(2013)05-0325-04
