溢流坝池式消力戽数值模拟及特性分析

陆周祺

（上海勘测设计研究院 上海 200434)

1 前言

池式消力戽作为一种重要的溢流坝消能形式，在水利工程中有着广泛的应用。当水流从堰面流至消力戽，下泄水流会在戽斗内产生逆时针旋滚，且戽斗的末端仰角将主流挑向下游水面，使出戽的水流在底部产生旋滚，在水面产生波浪和跌水，从而使池式消力戽达到良好的溢流坝消能效果。

实验测量方法以其结果的真实可信，成为溢流坝池式消力戽研究的一种有效手段，但由于模型比尺效应以及量测技术问题，使得原型的一些特性难以通过试验方法得到。随着计算流体力学的迅猛发展，数值模拟技术以其花费小、周期短以及易再现等优点，成为研究溢流坝复杂水流特性的有效工具。目前对于溢流坝的数值模拟，大多基于VOF方法，选用Standardε-k模型或RNGk-ε模型进行研究，未对不同紊流模型的影响进行分析。本文针对 VOF方法，同时采用标准k-ε模型、RNGk-ε模型以及Realizable k -ε模型进行数值模拟，分析了不同紊流模型对溢流坝池式消力戽数值模拟的适用性。

2 数学模型和计算方法

2.1 VOF方法

溢流坝堰面上的水流是一种复杂的气液两相流流动，由Hirt和Nichols提出的VOF方法（流体体积法)是计算流体力学中追踪和定位自由曲面或流体界面的数值技术。它使用静态或以某种确定形式迁移的网格以适应于界面形状的演化，是欧拉法的一种。流体体积法能够保持追踪流体的“质量”，并且能够容易的追踪拓扑结构变化的流体界面，其基本思想可简述为：定义α1和α2分别为堰面上水和气的体积分数，对于每一计算单元，水和气的体积分数之和恒为1。当α1=1表示该单元充满水，当α1=0表示该单元充满气体；而当0＜α1＜1表明该单元同时存在水和气，即存在自由水面。通过各相局部瞬时的控制方程以及两相间的关系可求得每一计算单元的α1和α2值，从而得到自由水面的位置。

2.2 计算区域

模拟模型采用东升水电站溢流坝的原设计方案尺寸，实测数据取自张铭等的物理模型实验结果。溢流坝采用标准 WES实用堰，戽斗反弧半径10.0m，挑角45°，尾端为长2.93m、1:1坡度的直线段，戽斗顶段长2.0m，堰面曲线总长约46.65m。x、y分别为纵向和垂向坐标，坐标原点位于堰顶处。取设计水位工况进行数值计算，设计水头为12.0m，流速为3.66m/s，采用二维非结构化网格剖分区域见图1。

2.3 数值方法、边界条件以及初始条件

采用有限体积法离散方程，对流项采用二阶精度的Quick格式离散，扩散项采用中心格式离散，而压力速度的耦合求解采用PISO算法。

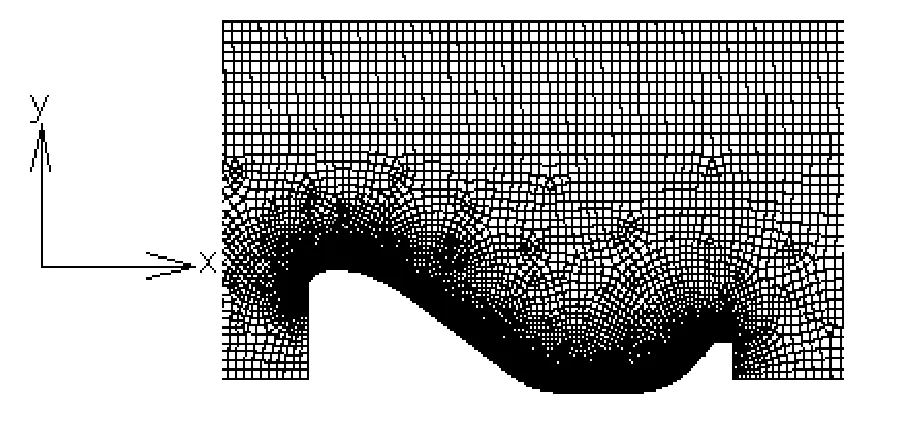
图1 计算区域网格示意图

上游进口分为下部的速度进口边界和上部的压力进口边界；气体边界采用压力进口边界条件；下游出口采用压力出口边界条件；其余采用壁面边界条件，对粘性底层采用壁面函数法来处理。在初始流场中，首先对上游水入口以下部分（一直延伸到出口)水的体积分数赋值为 1，即从水入口一直到出口处下面部分充满水，其余计算区域充满空气。

3 模拟结果及分析

3.1 水面线

图2为通过三种紊流模型计算所得的水面线与实测值的比较，从图2可看出，三种模型虽均有偏差，但整体均能较好地模拟水面线的变化趋势，这也说明 VOF方法能够很好地追踪自由液面，且从量值上看，Realizablek-ε模型要好于其余两种，主要水面线差异发生在掺气程度强烈的反弧段，标准k-ε模型计算值偏大，而RNG k-ε模型计算值偏小，Realizablek-ε模型与实测结果较为接近。

图2 不同模型和实测的水面线图

3.2 时均压力

图3为溢流面段和消力戽内的时均压力的数值模拟结果与实测值的比较，由图3可知，堰面顶部压力较小，且沿顺流方向逐渐增大；在消力戽内，受水体重力和水体离心力的共同作用，时均压力有较大升高。从三种紊流模型计算结果来看，时均压力的主要差异仍集中在反弧段，标准k-ε模型模拟结果误差较大，而Realizablek-ε模型的计算值更接近实验结果。

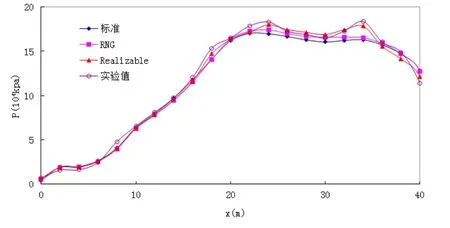
图3 不同模型和实测的压力分布图

3.3 综合流量系数

溢流坝的泄流能力受上游水位高低和闸门开度大小的控制，其泄流能力公式为：

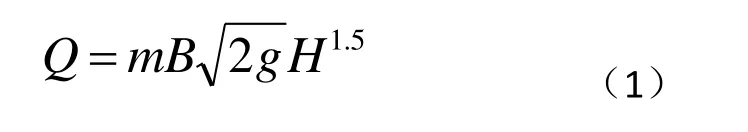
式中，Q为流量，B为溢流堰净宽，H为堰上水头，m为综合流量系数。根据式（1)计算不同紊流模型综合流量系数与实验值的比较见表1可知，标准ε-k模型的综合流量系数远大于实验值，误差为11.17%，RNGε-k模型和Realizableε-k模型的综合流量系数与实验值相差不大，且后者更为接近。

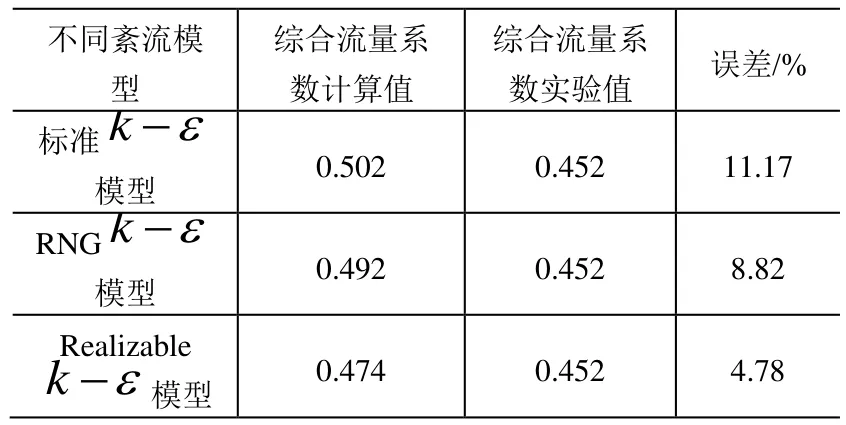
表1 不同紊流模型下综合流量系数比较

综上可知，Realizableε-k模型的整体模拟结果要优于其余两种，表现出了对溢流坝池式消力戽模拟的很好适用性。这主要是因为在上述三种模型中，标准ε-k模型假定粘度系数是各向同性的，即对于雷诺应力的各个分量，认为粘度系数是相同的，只能适用于简单的各项同性切变紊流，因而在模拟溢流坝池式消力戽这种弯曲流线情况下会产生一定失真；RNGε-k模型通过修正紊动粘度，考虑了平均流动中的较大曲率流动、旋流流动以及涡旋运动情况，但耗散方程中会产生奇异性，不能满足真实情况；而Realizable k -ε模型通过引入可变系数，考虑了旋转和曲率变化，保证了应变率很大情况下计算结果的可实现性，且耗散率控制方程不具有奇异性，这是与其余两种模型的最大区别之一，因此该模型对于溢流坝池式消力戽的模拟更为有效。

3.4 流态及消能特性

图4为通过Realizableε-k模型模拟而得的流线图，从图4中可看出池式消力戽兼具底流和戽斗面流的流态。水流经过堰面进入反弧段，在消力戽内行进一段距离后由末端的挑坎将水流挑向下游形成面流。消力戽和挑坎后各存在一个旋滚及其相应的负流速区域，挑坎下游水面有一不太陡峭的波浪，紧接波浪后面是一个不太剧烈的跌水，没有明显的二次残余旋滚，即池式消力戽并没有形成单圆弧消力戽的典型“三滚一浪”，而是呈淹没戽流流态。

池式消力戽的消能也兼具底流和戽斗面流的消能特点，水流以底流的形式进入消力戽，水流主要通过戽内的旋滚内部以及旋滚与主流之间的掺混进行消能，在戽内消耗部分能量后，进一步通过挑坎后的底部旋滚以及水面的波浪和跌水进行二次的能量耗散。

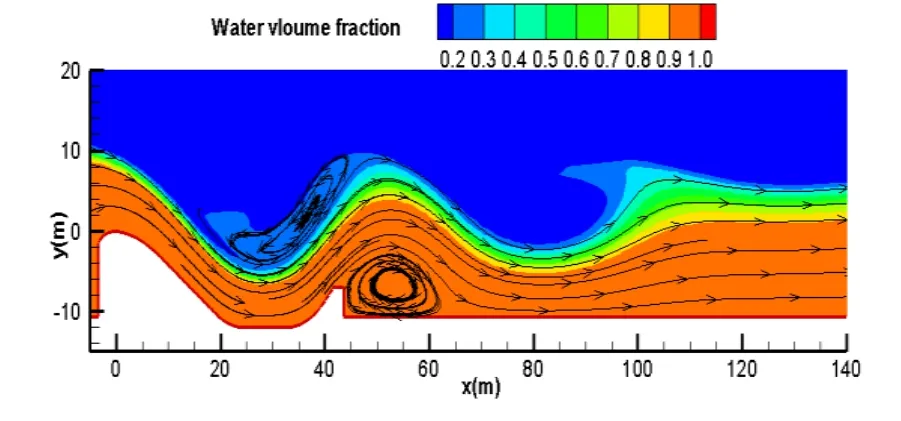
图4 Realizableε-k模型计算所得流线图

4 结论

本文基于VOF方法，分别采用了标准ε-k模型、RNGε-k模型以及Realizableε-k模型对溢流坝池式消力戽进行了数值模拟，通过对计算区域的水面线、时均压力以及综合流量系数的对比发现，Realizableε-k模型的整体模拟结果要优于其余两种，表现出了对溢流坝池式消力戽模拟的适用性。进一步地，以Realizable ε-k模型的模拟结果为基础，分析了池式消力戽的流态和消能特性，表明其兼具底流和戽斗面流两者的流态及消能特点。

1.耿运生, 车传金, 靳翠红.乱木水库溢洪道数值模拟[J].水科学与工程技术, 2006(5): 33-35.

2.赵振兴.中低水头闸坝枢纽布置与窄缝式戽式消力池消能问题的研究[D].硕士学位论文, 重庆交通大学, 2008,重庆.

3.邓毅国, 王毅鸣, 龙文.韩立土卡河水电站泄洪消能设计[J].云南水力发电, 2006(6): 33-37.

4.张延, 曹继文, 王丽学等.池式窄缝戽流消能计算方法研究[J].水动力学研究进展, 1996, 11(4): 459-464.

5.潘艳华, 杨敏.宽尾墩与戽式消力短池在满台城水电站中的联合应用[J].吉林水利, 1997(1): 16-19.

6.程香菊, 陈永灿, 罗麟.阶梯溢流坝水气两相流数值模拟[J].中国科学E辑, 2006, 36(11): 1355-1364.

7.李玲, 陈永灿, 李永红.三维 VOF模型及其在溢洪道水流计算中的应用[J].水力发电学报, 2007, 26(4): 83-87.

8.陈群, 戴光清, 刘浩吾.带有曲线自由水面的阶梯溢流坝面流场的数值模拟[J].水利学报, 2002(9): 20-26.

9.Launder B E, Spalding D B.Lectures in Mathematical Models of Turbulence[M].Academic Press, London,England, 1972.

10.王福军.计算流体动力性分析[M].北京: 清华大学出版社, 2004.

11.王世夏, 林益才, 沈长松.水工建筑物[M].南京: 河海大学出版社, 2007.