风电接入对继电保护的影响(六)
——风电场送出线路距离保护影响分析
2013-10-23张保会张金华郝治国
张保会,张金华,原 博,王 进,郝治国
(西安交通大学 电气工程学院,陕西 西安 710049)
0 引言
近年来,我国风力发电接入电力系统的数量越来越多,容量越来越大,至2011年底我国风电装机容量达62.3642 GW[1-3]。风电及其接入电网故障的快速、正确切除已成为保证电网安全运行的重要因素[4-7]。但风力发电集中接入区域电网与传统电网在故障期间的电磁暂态特性存在显著差异[8],传统的继电保护设备在大规模风电接入电网系统中能否正确工作,尚无系统的分析研究,现有保护在风电送出系统故障时的动作行为无法确定,单靠运行现场故障后的保护动作记录,不能给出现有保护的适用性,更难以提出普遍的改进原则。
文献[9]已经指出,双馈式风电场送出线路风电场侧保护测量处的电压、电流频率有所差别。其中,保护测量处电流的主要频率分量随短路前机组的转速变化,不再保持工频,频率变化范围为35~65 Hz,而保护测量处电压的主要频率分量一般可由系统支撑维持工频。本文从感应发电机基本原理出发,在转子转速旋转磁场坐标下,推导了感应发电机简化三阶动态模型,建立了感应发电机的暂态等值电路,进而从电路角度分析了风电场送出线电压、电流不同频率的机理,并在PSCAD仿真平台进行了验证。
由于风电场送出线路风电场侧电压、电流频率不一致,依据工频电压、电流相量的距离保护元件,以及基于线路的时域微分方程模型而不再涉及信号的频域信息的解微分方程算法距离元件的动作性能都需要进行细致的分析。
1 双馈风电场送出线路故障特征
在PSCAD/EMTDC电磁暂态平台建立某地区50 MW双馈式风电场集中式接入仿真系统,如图1所示。其中,风电系统及送出线路参数见文献[10],线路全长13.7 km,110 kV系统短路容量670 MV·A。

图1 风电场送出线路保护测试系统Fig.1 Test system of wind farm outgoing transmission line protection
检测系统发生故障时,双馈式风电机组(DFIG)转子回路投入Crowbar电路实现低电压穿越,该阶段时间非常短暂,线路保护来不及动作,此后DFIG相当于普通的异步感应发电机运行。仿真在t=0 s时刻在风电场送出线路中点处发生三相短路,故障过渡电阻1 Ω,故障持续时间0.1 s,故障前风速较小,所有风电机组运行转速为0.7 p.u.。为简化分析,认为故障后瞬时机组投入Crowbar电路,得到风电场侧电流I1、系统侧电流I2,以及风电场侧母线电压U1、系统侧母线电压U2,分别如图2和图3所示。

图2 系统电流与风电场电流Fig.2 System currents and wind farm currents

图3 系统电压与风电场电压Fig.3 System voltages and wind farm voltages
由仿真结果可以看出,双馈式风电场送出线路风电场侧保护测量处的电压、电流频率有所差别。系统侧故障电流主要频率分量为工频,风电场侧故障电流主要频率分量为0.7×50=35(Hz)。通过频谱分析计算,系统侧电流中35 Hz分量大小占50 Hz分量的1.3%,风电场侧电流中35 Hz分量大小是50 Hz分量的19.04倍。而系统侧及风电场侧故障电压主要频率分量均为工频,通过频谱分析计算,系统侧电压中35 Hz分量大小占50 Hz分量的6.2%,风电场侧电压中35 Hz分量大小占50 Hz分量的59.9%。
2 风电场送出线电压、电流不同频率机理
2.1 感应发电机暂态模型
感应电机转子运动方程[11]:

其中,s为电机转差率;τJ为惯性时间常数;Tm、Te分别为机械转矩和电磁转矩;D为阻尼系数。
感应发电机定、转子在各自三相静止坐标系下电压方程[12-13]:

其中,us= [uAuBuC]T、ur= [uaubuc]T分别为定、转子电压;is=[iAiBiC]T、ir=[iaibic]T分别为定、转子电流;rs=diag(Rs,Rs,Rs)、rr=diag(Rr,Rr,Rr)分别为定、转子电阻对角阵;ψs=[ψAψBψC]T、ψr= [ψaψbψc]T分别为定、转子磁链;p为微分算子。
定、转子磁链方程:


其中,θr为转子角度;Lmd为定、转子互感;Lsσ、Lrσ分别为定、转子漏感。
式(2)、(3)表明,在以上坐标系统中,交流电机为时变非线性耦合系统。按磁场等效及恒相幅值原则选择三相静止坐标系至αβ两相静止坐标系变换C3/2,及αβ坐标系至dq两相旋转坐标系变换CVR:

其中,θ为d轴与α轴间夹角,即转子位置角。
对式(2)、(3)依次进行 C3/2及 CVR变换(旋转变换转速取为转子转速),得到dq两相旋转坐标系下交流电机定、转子电压方程:

其中,Us=usd+j usq、Ur=urd+jurq分别为定、转子电压空间相量;Is=isd+j isq、Ir=ird+j irq分别为定、转子电流空间相量;ψs=ψsd+jψsq、ψr=ψrd+jψrq分别为定、转子磁链空间相量;ωr为转速角频率。
定、转子磁链方程:

其中,Lm=1.5Lmd为定、转子等效互感;Ls=Lm+Lsσ、Lr=Lm+Lrσ分别为定、转子等效自感。
式(1)、(6)和(7)即为感应发电机精确的暂态模型。为便于分析计算,需对电机的数学模型进行适当简化。感应电机暂态过程中,转子磁链增量对发电机暂态过程的影响远大于定子磁链增量所带来的影响,且电机定子部分暂态过程的时间常数远小于转子部分暂态过程的时间常数,因此本文在研究感应电机暂态过程中不考虑定子磁链暂态过程[11,14],即pψs=0。
根据式(7)消去转子电流,并且定义暂态电势E′=jωrψrLm/Lr来表示转子磁链,代入式(6)的定子电压方程中,得:

代入式(6)的转子电压方程中,得:

其中,暂态时间常数τd′=Lr/Rr;暂态电感L′=Ls-Lm2/Lr。
式(8)、(9)与转子运动方程式(1)构成感应发电机三阶动态模型,由式(8)可得感应发电机的暂态等值电路如图4所示。
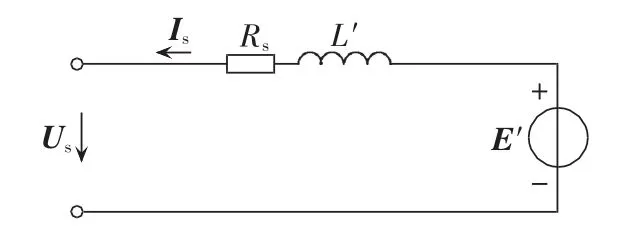
图4 感应发电机暂态等值电路Fig.4 Transient equivalent circuit of induction generator
运用图4简化等值电路可对含DFIG的系统进行近似故障分析。
2.2 DFIG故障特征分析
对于具备低电压穿越能力的DFIG,一般故障后数毫秒内闭锁转子侧变流器并投入Crowbar电阻。投Crowbar前,转子回路电压Ur≠0,转子电流仍受稳态时的矢量解耦控制规律的影响,暂态特性较为复杂。由上述感应式发电机暂态模型可知,暂态电势的变化规律与转子励磁电压有关。该阶段时间短暂,线路保护来不及动作,为简便分析,认为故障瞬时Crowbar电路投入,此时转子绕组自成闭合回路,转子电压Ur=0,DFIG相当于普通的异步发电机运行。
由于故障后无励磁电压,故转子磁链故障后的稳态值将为零,而在故障瞬时转子磁链不能突变,所以转子绕组中会感应出衰减的直流电流,其衰减时间常数τ′r=L′r/R′r,其中 L′r=Lr-L2m/Ls为从转子侧看进去的等值暂态电感,R′r=Rr+RCrowbar为转子绕组电阻与Crowbar短路电阻之和。即在转子旋转坐标系下,转子磁链只有衰减的直流分量:

因此故障期间电机的暂态电势为:

通过dq旋转坐标系至αβ坐标系变换CRV(旋转变换转速取为转子转速)以及αβ坐标系至三相静止坐标系变换C2/3:

可得三相静止坐标系下的暂态电势:

经整理,幅值最大相的暂态电势为:



由式(15)知,在故障暂态分析时,DFIG可以等效为经暂态电抗后的暂态电势,此电势的频率为对应于转子转速的频率,幅值按照指数规律衰减。以前述测试系统中 ωr=0.7ω1为例,ω1为工频角频率,DFIG等效于一个频率为35 Hz的暂态电势,其幅值的初值为 1.30 p.u.,以衰减时间常数τ′r=0.026 s衰减。经 4τ′r~5τ′r后,转子磁链基本衰减完毕,此时暂态电势约为零,DFIG可等效为无源负荷,其阻抗与转差有关,等值电路如图5所示。

图5 DFIG作为负荷时的等值电路Fig.5 Equivalent circuit of DFIG as a load
2.3 风电场送出线路故障分析
对于含DFIG的系统分析,故障期间电网中有2种频率的电源激励,对线性系统,须运用叠加原理分别对2种频率分量作等值电路进行故障分析。
以三相故障为例,从电路角度分析双馈风电场送出线两侧保护处测得的电压、电流。故障期间系统等值电路图如图6所示。

图6 故障期间系统等值电路Fig.6 Equivalent circuit of system during fault
图中,E1为风机暂态电势,频率取决于故障前机组转速;E2为系统电势,频率为工频;Z1为DFIG暂态电抗Zw、箱变阻抗ZT1、送出变阻抗ZT2以及汇流线阻抗(其值较小,可忽略)之和;Zl1、Zl2为送出线路阻抗;Z2为系统侧阻抗;Rg为过渡电阻。由于风电场的容量相对较小,风机出口电压很低,从高压侧来看,风电场侧的等值阻抗远大于系统侧的等值阻抗,即Z1远大于图6中的其他阻抗。
分别作出工频分量回路、非工频分量回路,如图7、8所示。上标“g”表示工频量,图中各阻抗为工频角频率ω1乘以相应电感;上标“f”表示对应于ωr的非工频交流量,图中各阻抗为角频率ωr乘以相应电感。

图7 工频分量回路Fig.7 Circuit loop of power frequency component

图8 非工频交流分量回路Fig.8 Circuit loop of rotor speed frequency component
分别运用电路原理求解2个电路,可得2种频率激励单独作用下的线路两侧电压、电流。并考虑到图7中Zg1远大于其他阻抗,图8中Zf1远大于其他阻抗,进行近似简化,得式(18)—(25)。

根据式(18)—(25),比较风电场侧保护安装处电压U1、电流I1,系统侧保护安装处电压U2、电流I2的工频分量与非工频分量的幅值,有以下结论:0,远小于,系统侧电流的主频为工频;,远小于,系统侧电压的主频为工频。和都较小,一般,即风电场侧电流的主频为非工频;,小于,风电场侧电压的主频为工频。因此,风电场侧保护测得的电流、电压主频不一致。
以第1节三相故障为例,用仿真模型中的具体参数进行解析计算,故障电路参数见表1(折算为标幺值),得到 U1、I1和 U2、I2的工频分量与非工频分量(35 Hz)的幅值。将其与用复杂的风机模型通过PSCAD平台仿真计算结果对比,如表2所示。
由表2知,解析结果和仿真结果在一定的误差范围内基本一致,从而验证了本文中用等值电路对含DFIG的系统进行近似故障分析方法的可行性。解析结果和仿真结果均表明,风电场侧保护处测得的电流、电压主频不一致,而系统侧电压、电流主频均为工频。

表1 故障电路参数表Tab.1 Parameters of faulty circuit

表2 送出线两侧电压、电流幅值Tab.2 Magnitudes of voltage and current at two sides of outgoing transmission line
3 电压、电流频率不一致对距离保护影响
3.1 对相量距离保护影响
文献[10]已经指出,工频傅氏算法只能滤除工频整数倍次谐波,当信号频率在工频附近偏移时,工频傅氏算法无法准确提取基频相量幅值与相位。
当保护安装处感受到的电压、电流主要频率成分不同时,经傅氏滤波提取所获得的电压、电流相量的旋转速度也会变得不同,经过幅值相位比较后获得的阻抗计算结果也会发生旋转,基于傅氏相量计算的距离元件将产生极大误差。
图9为一个典型的基于相量计算的距离元件计算的阻抗在阻抗平面上的运动轨迹。在故障后的短时间内(距离I段作用时间内),计算出的阻抗在阻抗平面上不断进出阻抗特性的动作区,从而造成基于相量计算的距离元件误动作。

图9 基于傅氏相量算法的距离元件动作结果Fig.9 Result of distance element based on Fourier phasor algorithm
理论上,由第2.3节分析,若分别准确提取保护安装处工频分量以及转速频率交流分量电压、电流,则可以有效测量出故障线路阻抗。
根据图7工频分量回路,由系统侧保护安装处的工频电压、电流信息可以计算得到故障点到系统侧保护安装处的线路阻抗。需要注意的是,由风电场侧保护安装处的工频电压、电流信息计算的阻抗值为负,其含义为风电场背侧阻抗,不再是故障点到风电场侧保护安装处的线路阻抗。
同样地,根据图8非工频分量回路,由风电场侧保护安装处的非工频电压、电流信息可以计算得到故障点到风电场侧保护安装处的线路阻抗;而由系统侧保护安装处的非工频电压、电流信息计算的阻抗值为负,其含义为系统背侧阻抗,不再是故障点到系统侧保护安装处的线路阻抗。
以图1系统线路中点三相金属性故障为例进行分析,首先利用Prony算法或最小二乘算法等准确提取线路系统侧工频电压、电流信息,进而计算出系统侧故障阻抗2.92 Ω;提取线路风电场侧非工频(35 Hz)电压、电流信息,进而计算出风电场侧故障阻抗为2.66 Ω,在误差范围内可以有效反映出故障线路的阻抗(线路一半阻抗为2.89 Ω)。
3.2 基于解微分方程算法距离保护
解微分方程是基于线路RL时域模型而设计的算法,与信号的频率没有直接的联系。因此,从原理上,使用解微分方程算法可以避免傅氏滤波相量距离保护算法存在的问题。
对典型的线路等效RL模型列写出线路端口处电压、电流的时域数学模型如下[15-16]:

其中,u在相间故障下为两故障相间的相电压差,在单相故障下为故障相的相电压;i在相间故障下为两故障相间的相电流差,在单相故障下为故障相的相电流。
将参与计算的数据窗内采集获得的电压、电流数据代入式(26),将获得一个超定方程组,对方程组进行最小二乘拟合即可获得对应故障回路的电阻R和电感L,从而可以根据该电感L计算出故障点到保护安装处的距离。
对图1仿真系统进行离线分析,采用最小二乘算法求解线路的微分方程,时间窗长度取半个周期,从故障发生后10 ms开始进行计算。经对仿真模型获得的电压、电流采样数据进行计算,得到解微分方程的计算结果如表3所示。
由于风机故障电流的频率在35~65 Hz之间变化,在解微分方程算法的适用频带内。因此解微分方程算法在风电暂态电压、电流作用下仍然可以保证计算结果的正确性,相对于傅氏滤波相量算法而言更加适用于风电场送出线路的距离保护元件中。

表3 解微分方程算法距离保护计算结果Tab.3 Results of distance element employing differential equation algorithm
4 结论
风电场电流频率取决于转速,可能非工频,电压由电网支撑为工频,因此风电场送出线路的保护安装处电压与电流主要频率分量不一致。基于傅氏相量算法的距离元件计算结果受到十分严重的影响,无法正常工作。分别准确提取保护安装处工频分量以及转速频率交流分量电压、电流,可以准确测量出故障线路阻抗。解微分方程算法在风电场暂态电压电流下计算结果基本不受影响,宜在风电场送出线路的距离保护中使用。
