大直径管道磁致伸缩纵向导波传感器偏置磁场的优化设计

马宏伟，张喆斯，宋振华

（1.暨南大学 理工学院，广州 510632；2.暨南大学 “重大工程灾害与控制”教育部实验室，广州 510632）

运输管道在投入使用一段时间后其内部或表面易出现损伤，对公共安全造成一定威胁，因此对管道进行快速、准确、高效的检测十分重要。常规的管道超声波损伤检测技术都以逐点扫描的方式进行检测［1］，对于工业中的长距离管道进行检测，存在代价高、效率低的缺点［2］，而新型的超声导波管道检测技术是基于Rayleigh和Lamb［3］等关于有界介质中超声导波的传播理论研究而提出的。检测原理为利用传感器在管道一端激励超声导波，导波沿着管道纵向传播时遇到缺陷会发生反射、透射，利用另一传感器接收反射波或透射波，并根据回波信号的时间和幅值确定损伤位置及其程度。因此该技术对于检测细长型的管道结构有较大的优势，能够实现管道的快速低成本检测。在各种管道检测技术中，超声导波检测技术具有单点检测、传播距离长等优点［4］。目前，在超声导波管道检测中所使用的传感器主要有压电式传感器（PZT）、磁致伸缩式传感器（MsS）、电磁声传感器（EMAT）、脉冲激光式传感器和PVDF式传感器等［5］，其中压电式传感器的应用较为广泛。磁致伸缩传感器相比于传统的压电式传感器，具有可实现对任意截面结构的检测、能量转化效率高、能适应各种高温的检测环境等优势，避免了压电式传感器必须与结构完全耦合的缺点，属于非接触式的传感器［6－7］。

Kaule［8］于20世纪50年代首次提出了基于磁致伸缩效应的超声导波无损检测技术。Kwun［9－10］阐述和分析了磁致伸缩超声导波传感器长距离检测的优点，并采用磁致伸缩超声导波传感器对钢丝绳的断丝情况进行了检测。Kwun，J.Hanley和Holt［11］通过试验表明了磁致伸缩超声导波传感器能够用于钢管腐蚀坑的检测，证明了磁致伸缩超声导波法对于不同类型的损伤均可实现无损检测。武新军［12－13］等人详细论述了管道用磁致伸缩超声导波检测系统的组成，研制了相关试验装置进行信号检测，现场试验结果表明磁致伸缩传感器用于管道导波检测的可行性、有效性和实用性。金建华［14］等人利用磁致伸缩式超声导波传感器激励了周向导波信号对大直径管道进行了损伤检测。柯岩［15］等人进行了基于磁致伸缩技术的钢管无损检测试验研究，但其试验管道属于直径为38mm的小直径管道。程涛［16］等人开展了管道超声导波磁致伸缩传感器的研发工作，对直径51mm的管道进行了裂纹检测。因此在国内，磁致伸缩纵向导波技术对大直径管道的无损检测研究尚处于起步阶段。笔者在此基础上试验选择适用于大直径管道上的超声导波磁致伸缩传感器阵列方法和布置原则。大直径管道中偏置磁场由于管径较大的原因而呈现磁场强度弱、分布不均匀的特点。而传感器偏置磁场在管道中的磁场分布情况直接影响了传感器对于导波的激发与接收。因此，笔者对大直径管道中偏置磁场的分布情况进行了数值计算，通过截面磁场分布方差来衡量截面上磁场的均匀性，从而设计出适用于大直径管道的偏置磁场最优化布置，为磁致伸缩传感器在大直径管道上的应用提供了布置原则及其理论基础。

1 磁致伸缩管道检测的理论基础与偏置磁场设计

1.1 磁致伸缩效应与传感器组成

铁磁体在被磁化时其长度和体积均会发生变化，这种效应被称为磁致伸缩效应。反之，称为磁致伸缩逆效应［17］。磁致伸缩式超声导波传感器利用了铁磁体的磁致伸缩效应激发超声导波；及其逆效应来接收超声导波，以实现管道的无损检测。

如图1所示，部分管道处于静态偏置磁场下，当交变电流通过激励传感器线圈时会产生出交变磁场，导致该部分管道内的纵向应变，从而激发纵向超声导波。超声导波沿着管道纵向传播，经过接收传感器时由磁致伸缩逆效应引起接收线圈的电压变化而实现导波信号的接收和识别。

图1 磁致伸缩效应在管道检测中的应用

磁致伸缩传感器主要由两部分组成：①内层激励／接收线圈。作用为产生交变磁场作用于管道（激励线圈）和接收相应的交变磁场变化产生的感生电动势（接收线圈）。②外层偏置磁场。其主要作用为适当提高铁磁体的磁化强度，增强传感器的灵敏度。

在激励／接收线圈的设计中，为了增强磁致伸缩效应，考虑导波的叠加原理，采用三段式密绕线圈［18］，如图2所示。其中，两侧段线圈的绕制方向与中段相反，并且每段长度均为半波长l：

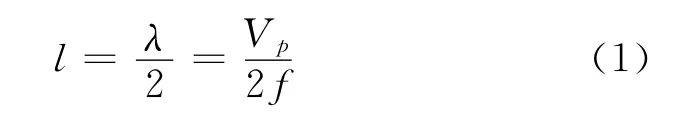
式中：λ为导波波长；f为导波中心频率；Vp为中心频率所对应的导波相速度。

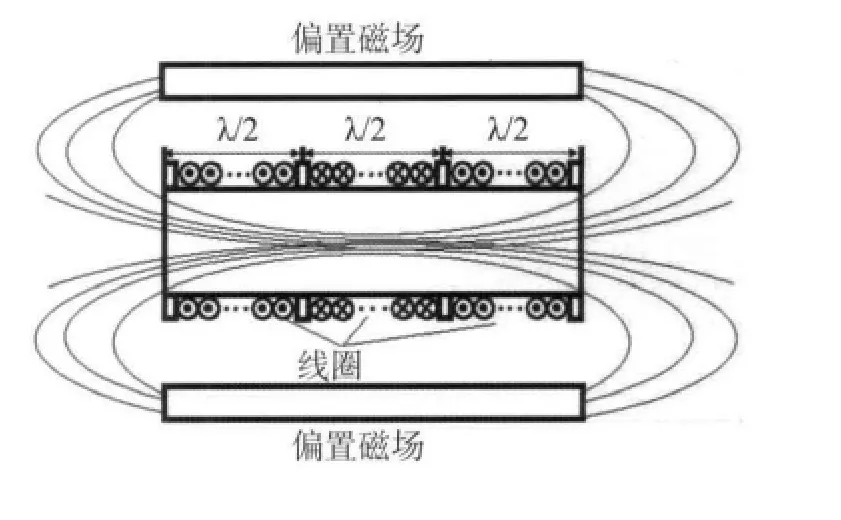
图2 三段式线圈示意图

在利用纵向超声导波检测时，需要根据导波在管道中传播的频散曲线来确定所需激发的中心频率。根据式（1），中心频率的大小直接影响了传感器内层每段线圈的绕制长度，从而影响了外层偏置磁场所需覆盖的区域长度。

1.2 偏置磁场的磁路设计及其数值计算

磁致伸缩超声导波管道检测的实现，主要取决于静态偏置磁场的合理设计。偏置磁场需满足磁源纯净、磁路简单、长期稳定等要求。文献［19］的研究表明，随着偏置磁场强度的增加，磁致伸缩效应及其逆效应的能量转换效率先提高，到达最优值点后又随偏置磁场强度的增加而降低，如图3所示。因此，需要对静态偏置磁场进行优化设计，以达到磁场强度和分布的最佳效果。笔者以永磁体作为静态偏置磁场的激励源，以分析磁场强度及分布对导波激励和接收的影响。过强、过弱及不均匀的静态偏置磁场都会导致导波无法激励和接收以及激励强度不够等问题。三磁路静态偏置磁场由三组永磁体磁路组成，每组磁路由两块高度方向充磁的永磁体、与构件连接的两块鞍片以及一块导磁轭铁组成，如图4（a）所示。

为了使得铁磁体管道中的磁致伸缩效应达到最佳效果，静态偏置磁场在管道截面上的最佳磁场强度应选择为铁磁体材料最大磁导率附近的磁场强度，且该磁场在整个管道截面为均匀分布。在工业和民用管道中，直径88毫米的大直径管道为应用最为广泛的管道种类和型号之一。因此，笔者以上述一组磁路作为一个单元，利用有限元计算讨论适用于大直径管道（φ88mm）检测的磁路组偏置磁场最优布置方案及其规律。

模型采用SolidWorks建模并通过Ansoft Maxwell软件实现该磁场强度及分布的数值计算。各部件模型如图4（b）～4（e）所示，其参数如表1所示。

表1 磁路组各部件模型参数 mm

为讨论磁路组个数对偏置磁场的影响，通过仿真模拟，分别计算了磁路组个数为n＝3，4，5，6，7个偏置磁场的磁场强度及分布情况。利用Ansoft进行三维磁场分析时，管道网格划分为10000个四面体单元，每个磁路组的网格划分为8000个四面体单元以确保计算精度。同时，为达到较理想的磁场分布，磁路组沿管道周向均匀阵列布置，如图5所示。

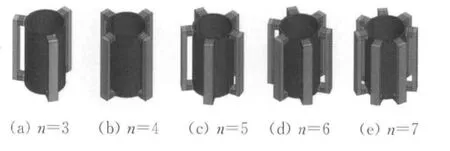
图5 传感器不同磁路组个数阵列示意图

2 结果分析与讨论

由于磁路组个数不同，每种磁路下相同截面的磁场强度分布情况不同。加之磁场沿铁磁体管道纵向上能量有所耗散，因此在相同的磁路组个数的情况下，管道上各个截面的磁场强度分布也会有不同。为客观反映偏置磁场在管道横截面上的分布情况，分别在磁路组覆盖区域的管道端部及其覆盖区域的中部选取两个截面，并在每个截面处周向均匀选取8个节点作为磁场强度采样点，如图6所示。

通过仿真计算可以得到磁路组覆盖区域中管端面及其中截面上磁场强度云图，如图7，8所示。从图中可以看到，在同一截面上，当磁路组个数较少时，磁场在管端截面的分布略不均匀，随着单元数的增加，磁场分布逐渐趋于均匀。而中截面上的磁场分布比上截面的更为均匀。

为衡量管道周向磁场强度分布的均匀程度，定义截面磁场分布方差如下：

图6 采样截面及采样点分布示意图

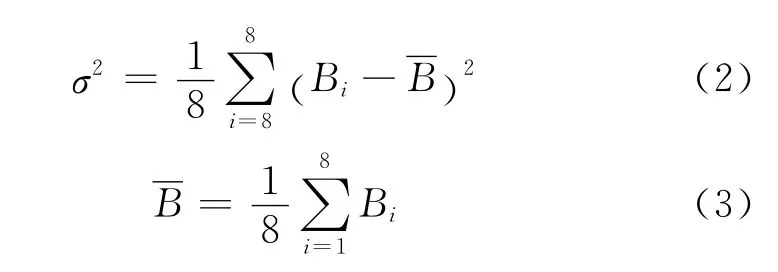
式中：Bi为该截面各采样点的磁场强度值（i＝1，2，…8为该截面8个采样点磁场强度的算术平均值。

由上式可以计算得到的各截面磁场强度方差，如表2所示。

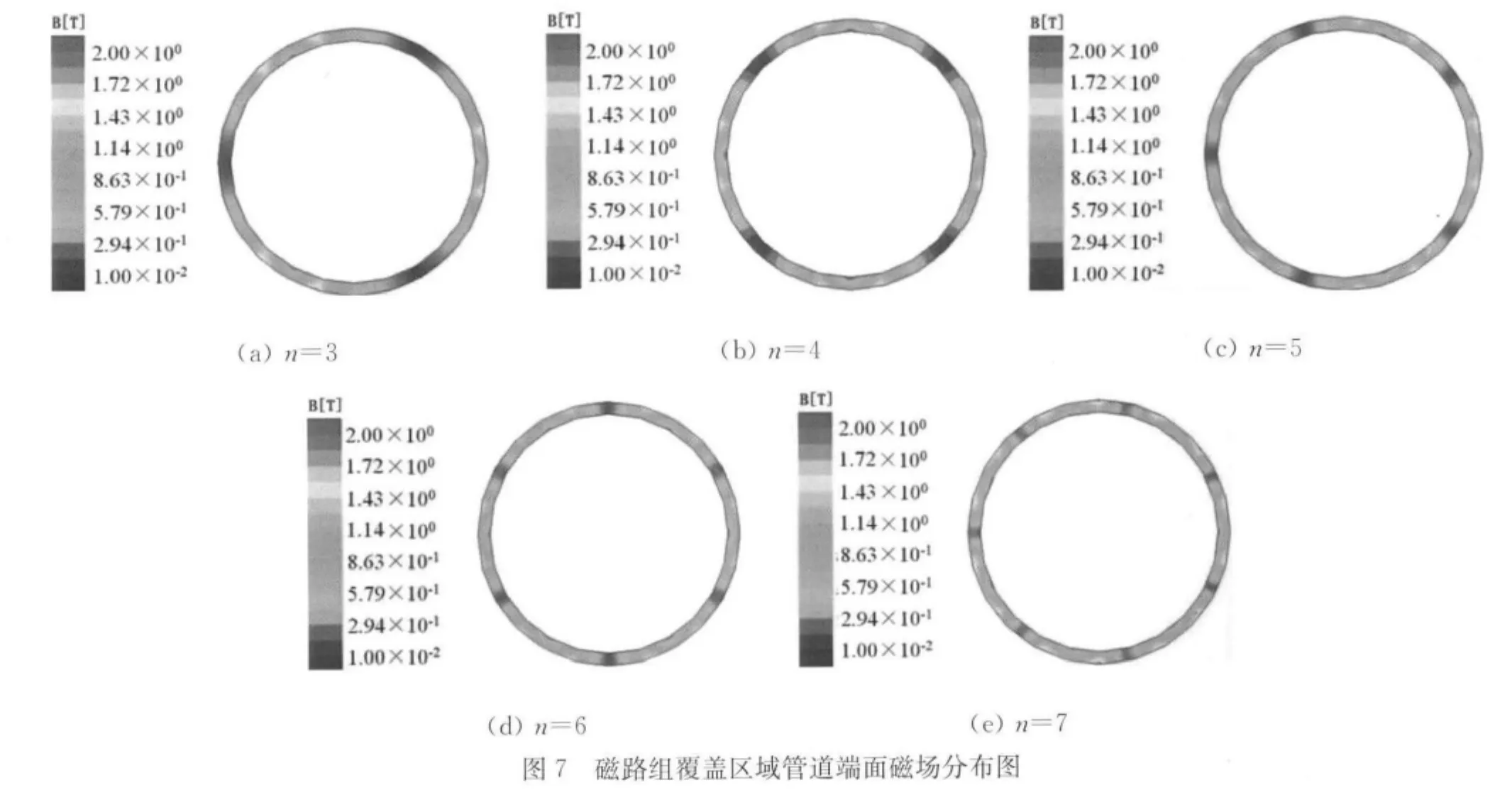
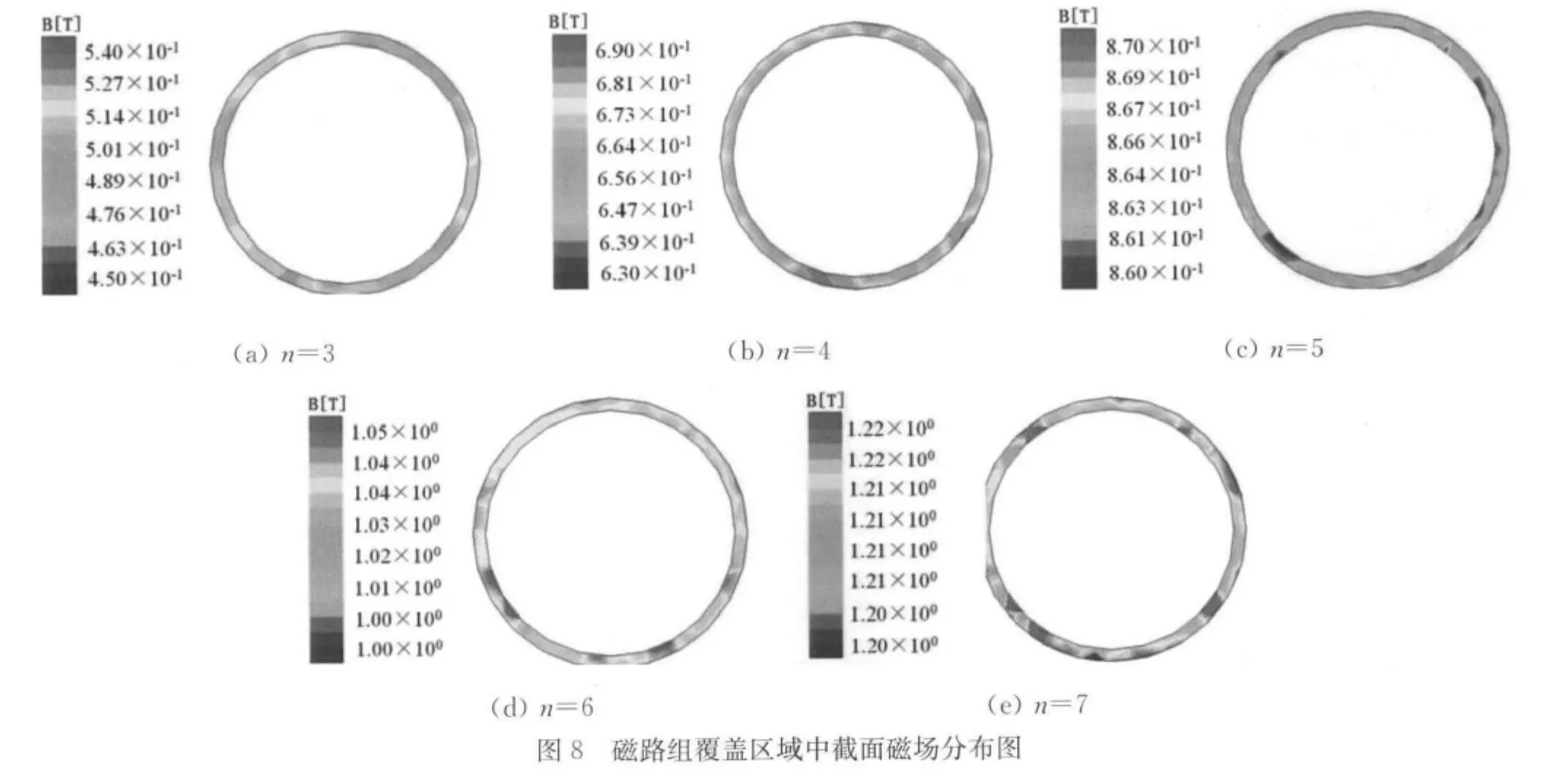
表2 磁路组覆盖区域管道端部、中截面处的磁场强度方差对照表

通过将采样点数据进行拟合，得到磁路组覆盖区域上管道端部和中截面磁场分布方差与磁路组个数的关系曲线，如图9所示。周向已较为均匀。

图9 各截面磁场分布方差与磁路组个数关系图

随着磁路组个数的增加，磁场总能量增大。管道上同一点的磁场强度绝对值也随之增大。同时，沿管道纵向从端部至中截面处，由于磁场能量的均匀化，中截面处磁场强度的最大值比磁路组覆盖区域其他节目上该值都要小。同时，为研究磁路组个数对磁场强度分布的综合影响，从数值计算结果可知磁路组个数与中截面磁场强度平均值的关系曲线如图10所示。

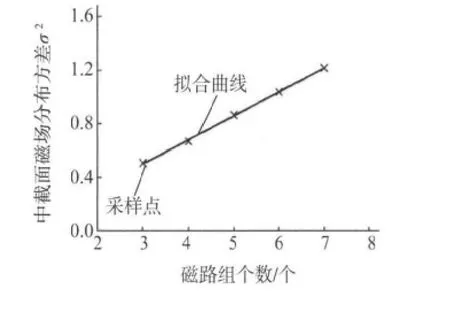
图10 中截面平均磁场强度与磁路组个数的关系

对比图9（a），9（b）可知，在相同磁路组个数情况下，磁路组覆盖区域的管道端截面与中截面的磁场分布方差在量级上相差很大。而中截面上的磁场分布比端截面更为均匀，这是由于端截面比中截面更靠近磁路组中永磁体激励源而引起的磁场不均匀。因此，偏置磁场的优化设计中，应选择中截面处的管道磁场强度作为偏置磁场的强度衡量标准。

同时，由图可知，对于端截面以及中截面上的磁场分布方差随着磁路组个数n的增加而明显下降，其呈现对数型衰减关系；但当n大于5时该方差的下降趋势趋于平缓。由于该方差反映得是磁场分布得均匀性，且方差越小表明磁场强度沿管道周向越均匀。因此，增加磁路组个数能较好地提高管道中偏置磁场的均匀程度。但在n大于5后，单纯以增加磁路组个数的方式已无法再显著的改善管道周向磁场强度的均匀性。此时，磁场强度的分布在管道

由图10可知，中截面磁场强度平均值与磁路组个数n成单调线性递增关系，这是由于磁场强度的可叠加性所致。通过拟合得到平均磁场强度B（T）与单元数n的关系式如下：

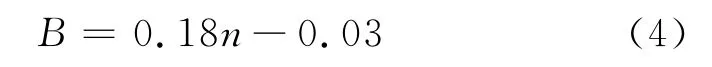
该关系式为直径88毫米管道磁路组个数与磁场平均强度的计算公式；利用笔者所提供的分析方法，同理可得到其他不同管径下管道的磁路组个数与磁场平均强度的计算关系式，以便于工程计算和应用。

对于一般铁磁材料，磁场最大磁导率的磁场强度为0.5T左右［20］。由图10可知，所计算的各磁路均已满足该磁场强度的要求，3磁路（n＝3）设计时的磁场强度最接近铁磁体的最优磁场强度。但从图9（b）可知，3磁路设计的磁场分布均匀性较差。因此，综合考虑磁场强度和均匀性等方面的要求，对于外径88mm壁厚4mm的大直径管道而言，选择5磁路（n＝5）的设计时，中截面平均磁场强度为0.87T，虽然不是最优磁场强度，但在保证磁场分布较为均匀的情况下其值最为接近最优磁场强度。该设计可为磁致伸缩超声导波传感器提供最优化的偏置磁场强度及分布方案。

3 结论

当磁路组个数较少时，磁场分布方差较大，在磁路组个数不变的情况下，管道中不同位置的截面上磁场分布情况也不相同。在本算例中，磁路组覆盖区域的管道中截面处磁场强度平均值与磁路组个数呈单调线性递增关系。并满足线性表达式B＝0.18n－0.03的关系，可以通过笔者提供的思路设计出其他不同管径管道磁路组个数与偏置磁场的简单公式以便工程计算和应用。

考虑磁场强度及分布的均匀性、磁场最优值点、传感器成本等因素，对于本算例中外径88mm壁厚4mm的大直径管道而言，选择5磁路（n＝5）的设计可为磁致伸缩超声导波传感器提供最优化的偏置磁场强度及分布。同理，其他管径管道的磁场强度及磁路个数可按照笔者提供的方法和思路进行有效的优化设计，以达到最优的导波激发和接收效果。

［1］焦敬品，何存富，吴斌，等.管道超声导波检测技术研究进展［J］.实验力学，2002，17（1）：1－9.

［2］程载斌，王志华，马宏伟.管道应力波检测技术及研究进展［J］.太原理工大学学报，2003，34（3）：426－431.

［3］HAYSHI T，TAMAYAMA C，MURASE M.Wave structure analysis of guided waves in a bar with an arbitrary cross－section［J］.Ultrasonics，2006，44：17－24.

［4］LOWE M J S，ALLEYNE D N，CAWLEY P.Defect detection in pipes using guided waves［J］.Ultrasonics，1998，36：147－154.

［5］何存富，刘增华，吴斌.传感器在管道超声导波检测中的应用［J］.传感器技术，2004，23（11）：5－8.

［6］KWUN H，BARTELS K A.Magnetostrictive sensor technology and its applications［J］.Ultrasonics，1998，36：171－178.

［7］叶宇峰，程茂，夏立，等.高温管道腐蚀状况的超声导波检测［J］.轻工机械，2009，27（3）：57－60.

［8］KAILE W.Magnetostrictive Ultrasonic Testing of Materials［C］／／Proceedings of the 4th International Conference on Non－destructive Testing. London：1964：291.

［9］KWUN H，TELLER C M.Detection of fractured wires in steel cables using magnetostrictive sensors［J］.Materials Evaluation，1994，52（4）：503－507.

［10］KWUN H，KIM S Y，LIGHT G M.The Magnetostrictive Sensor Technology for Long Range Guided Wave Testing and Monitoring of Structures［J］.Materials Evaluation，2003，61（1）：80－84.

［11］KWUN H，HANLEY J J，HOLT A E.Detection of corrosion in pipe using the magnetostrictive sensor technique［J］.NDT＆E Int，1997，30（2）：33.

［12］柯岩，武新军，康宜华，等.基于磁致伸缩效应的钢管导波检测可行性［J］.无损检测，2007，29（3）：113－116.

［13］武新军，徐江，沈功田.非接触式磁致伸缩导波管道无损检测系统的研制［J］.无损检测，2010，32（3）：166－170.

［14］金建华，申阳春.一种用于管道检测的磁致伸缩式周向超声导波传感器［J］.传感技术学报，2004，4：576－579.

［15］柯岩.基于磁致伸缩导波的钢管无损检测实验研究［D］.武汉：华中科技大学，2006：37－42.

［16］程涛.管道裂纹磁致伸缩导波检测传感器研制与开发［D］.武汉：湖北工业大学，2012：37－51.

［17］王博文，黄淑瑛，黄文美.磁致伸缩材料与器件［M］.北京：冶金工业出版社，2008：1－6.

［18］吴斌，刘秀成，何存富.兆赫兹纵向模态磁致伸缩传感器的设计及其在钢绞线中的试验研究［J］.机械工程学报，2011，47（22）：148－153.

［19］竺冉，吕福在，唐志峰，等.磁致伸缩纵向导波传感器中偏置磁场的优化设计［J］.传感技术学报，2011，24（3）：371－374.

［20］柯松，张辉，倪泽均，等.常用钢材磁特性曲线速查手册［M］.北京：机械工业出版社，2003：14－85.